Решение задач Коши для системы уравнений, описывающей одномерный поток гранулированного материала

В работе [1] описана математическая модель потока частиц гранулированного материала, уравнения которой содержали высоту и среднюю скорость в глубине потока как функцию времени и тангенса угла наклона направления потока к вертикальной оси. В [2] были выведены уравнения в более общей форме для одномерного потока гранул в движущимся цилиндре. В [3] было проведено подробное исследование таких уравнений, найдены их инвариантные решения. Ниже представлено решение задачи Коши для системы, полученной в [2], с использованием законов сохранения специального вида.

Будем искать функции и(х, t) и h(х, t), удовлетворяющие системе ht + uhx + uxh = 0, ut + uux + phx = 0        (1)

и условиям

h ( x , 0) = h ₀( x ), u ( x , 0) = 0 ,             (2)

где h - толщина; и - средняя скорость частиц в глубине потока; t - время; х - пространственная координата; h ₀ ( x ) - непрерывная финитная функция, в = const .

Введем следующие обозначения: [ a , b ] - носитель функции h ₀ ( x ), M = ( 1 1 , 0), N = ( 1 ₂,0), a <  1 1 <  1 ₂ <  b .

Уравнения характеристик системы (1) и их соотношения следующие:

dx = ( u ± л/p h ) dt , u ± 2 Jeh = const

Законы сохранения для системы (1) можно записать в виде At + B_x = 0 , где Л и В - функции, зависящие только от и и h .

Следствия законов сохранения имеют вид

^- h • A h ^{- u} • A u ⁺ B = 0, ^{- u} • A h -p- A u ⁺ B h = 0. ⁽³⁾

Характеристики системы (3) таковы, что u ± 2 /p h = const .

Сделаем замену z = u + 2phh, k = u - 2phi . Тогда система (3) в новых переменных имеет вид z • Az = Bz, k • Ak = Bk .              (4)

Запишем закон сохранения в эквивалентной форме:

J - Adx + Bdt = 0 .              (5)

MNP

Проведем из точек М и N две характеристики различных семейств и обозначим точку пересечения Р . Используя законы сохранения для однородных квазилинейных гиперболических систем [4], найдем координаты точки Р и значение функций и и h в ней.

Представим интеграл по криволинейному треугольнику MNP в виде суммы трех слагаемых, учтем уравнения характеристик системы (1) и проинтегрируем по частям:

j- Adx + Bdt = J ( - Au + A VP h + B ) dt = t ( - Au + A VP h + B )| P - NP              { k = k ₀ }                                  ^N

- J t •d _z ( - Au + A л/p h + B ) dz .

{ k = k 0 }

Положим

тогда

( dz (-Au + A^ph + B)|

I k = k ₀

= 0 ,

J - Adx + Bdt = t p ( - Au + A J p h + B ) , NP ^P J - Adx + Bdt = - t p ( - Au - A J p h + B ) PM ^P

при условии

^

d k ( - Au - A-J p h + B )|

I z = z 0 ,

= 0 .

Теперь равенство (5) примет вид

1 2                    ,

J Adx = 2 t _p ( A Vp h ) .

'p

Функции A , В должны удовлетворять системе (4) и краевым условиям (6), (7). Наиболее простое решение этой задачи такое:

A = ( ^{z - k} 0 ) ^{1/3 -} ( ^{k - z} 0 ) ^{1/3 -} ( ^z 0 ^{- k} 0 ) ^1/3,

B = 4 ( z ^- k 0 ) ^1/3 ( z ^{+ 3} k 0 )^- 4 ( k ^- z 0 ) ^1/3 ( k ^{+ 3} z 0 ) ,

где z 0 = 2 Tp V h 0 ( / D , k 0 =- 2 Tp hMl^ .

По формуле (8) окончательно получим:

t p =p^{- 1/2} ( ^^h ;( l i) + hhik) ) ^{- 1} ( i 1 - 1 2 ) +p^{- 1/2} x

x(рем+hyp,)"" J [(■№+■№)"’+ l1 ^

+ (T h 0( x ) + 7 h 0 ( l ^)    I dx .

Вернемся к интегралу (5). Рассуждая подобно тому,

как описано выше, можем записать:

J - Adx + Bdt =

NP

J

{ k = k ₀ }

- A +

B

dx =

- A +

<

B u -Tph

t ^{p x}

7 N

- J    x •Э _z - A +----

{ k = k 0 }    I     ^{u -}VP ^h

J - Adx + Bdt —

PM

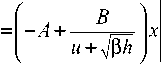
P

-

M

J    xAk

- A +

B

dz ,

dk .

Будем искать функции A и В , удовлетворяющие сис

теме (4) и условиям

Математика, механика, информатика

д z

/7

- A+"B- u-VPh k-k

IV            kK ^— k

^

— 0,

Значения функций в точке Р следующие: u ⁽ x P , t p )^—> (7 7 0 7 7 7^—7 h 0 ^{( z} 2 )),

д _k

— A+ u+7Ph

^

— 0.

(7 7 7 7 7+>07 / 27 )²

h ⁽ x P , t p ) ^—----------г---------

Системы (4), (10) имеют следующие решения:

⁴ ( z ^— к о )

A             1/3

( z 0 — ^k 0 )   ( z 0 ^{+ 3 k} 0 )

1/3

⁴ ( ^k — z 0 )

1/3

( z 0 — ^k 0 )   ( ^k 0 ^{+ 3} z 0 )

Таким образом, формулы (9), (12), (15) определяют функции и ( х , t ) и h ( х , t ) в криволинейном треугольнике, ограниченном отрезкам [ а , Ъ ] оси А 'и характеристиками, проведенными из точек ( а , 0) и ( Ъ , 0)

1/31/3

(z — k0 )   (z + 3 k0 )    (k — z 0 )   (k + 3 z 0 ).

B               1/3                             1/3

(z 0 - k 0 )   (z 0 + 3 k0 )  (z 0 - k0 )   (k0 + 3 z 0

Отсюда равенство (5) примет вид

^Z ?                  в TP h

J Adx — 2 x_{P 7}

/            ( u + 7P h )( u -Te h )

+

P

, Au — A л] в h — B

²    u — VP h

/ Au + A^ в h — B ( / ₂,0)    ^{1      u +}V^e h

.

( / 1 ,0)

Учитывая выражения для 1 ₀, k ₀ , после упрощений

получим:

x _—        4 h , / . уМ7 ( / 1 — / 2 )

^%P (Т^й—37ш7)(>07 / ^+>07 / 27)