Решение задач на собственные значения для уравнения Гельмгольца методом точечных источников поля
Автор: Щербакова Елена Евгеньевна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 3 (86) т.16, 2016 года.
Бесплатный доступ
Разработан способ решения задач вычисления собственных значений и собственных функций для уравнения Гельмгольца в областях с произвольной конфигурацией. При разработке способа численного решения задач используется метод точечных источников поля (МТИ). Предлагаемый способ основан на анализе числа обусловленности системы МТИ или погрешности численного решения задачи. Вводится понятие «критерий собственных значений». Результатом работы является разработанный эффективный алгоритм решения задач на нахождение собственных значений и собственных функций для уравнения Гельмгольца. Показано, что при приближении параметра Гельмгольца к собственному значению задачи число обусловленности системы МТИ и погрешность численного решения резко возрастают. Определив зависимость погрешности численного решения задачи или числа обусловленности системы МТИ от параметра Гельмгольца, можно по расположению максимума для полученных зависимостей найти собственные значения уравнения Гельмгольца в заданной области. После нахождения собственного значения можно приступить к нахождению собственных функций. При этом, если собственное значение оказывается вырожденным, то есть ему соответствует несколько собственных функций, то, с учетом симметрии области решения, возможно нахождение всех собственных функций. Приведены результаты решения тестовых двумерных и трехмерных задач, на основании которых делается вывод об эффективности предложенного метода.
Метод точечных источников, собственные значения, собственные функции, уравнение гельмгольца, фундаментальное решение, метод фундаментальных решений
Короткий адрес: https://sciup.org/14250233
IDR: 14250233 | УДК: 519.63 | DOI: 10.12737/20227
Текст научной статьи Решение задач на собственные значения для уравнения Гельмгольца методом точечных источников поля
Введение. Важное прикладное значение при разработке электромеханических, оптоэлектронных и радиотехнических устройств имеют задачи математической физики. Ряд таких задач приводит к решению однородного уравнения Гельмгольца
A U (r ) + X U (r ) = 0
с положительным значением параметра Гельмгольца λ>0. Это широкий класс задач, связанных с установившимися колебаниями (механическими, акустическими, тепловыми, электромагнитными и др.). Численное решение задач массой теплопереноса также приводит к уравнению Гельмгольца, уже с отрицательным значением параметра λ<0.
*
**
Важность решения уравнения Гельмгольца обусловлена также тем, что любые уравнения эллиптического типа с постоянными коэффициентами приводятся к уравнению этого вида.
При решении ряда прикладных задач требуется нахождение собственных значений и собственных функций для уравнения Гельмгольца в областях с различной конфигурацией. Аналитическое решение таких задач, а также чис- ленное решение с использованием традиционных численных методов, может вызвать значительные трудности и не всегда целесообразно, особенно если область решения имеет сложную конфигурацию, а граничные условия содержат производную по нормали.
Одним из эффективных методов численного решения граничных задач для ряда уравнений эллиптического типа является метод точечных источников поля (МТИ) [1–7]. Этот метод применяется при моделировании электрических, магнитных, тепловых, концентрационных, упругих напряжений и других физических полей [8–17]. Преимуществом МТИ является его простота и значительно меньший объем вычислений в сравнении с традиционными численными методами решения граничных задач, такими, например, как метод конечных элементов (МКЭ). Применение МТИ может быть оправдано также при решении задач на собственные значения для уравнений эллиптического типа, например, уравнения Гельмгольца [18, 19].
Описание численного метода. Пусть в области Ω выполняется уравнение Гельмгольца (1), а на границе ∂Ω области Ω заданы условия вида
a( r) +e( r)U
^ ' r ^ dQ , do
где α, β, γ — непрерывные функции, заданные на границе ∂ Ω области Ω.
Для нахождения неизвестной функции U ( r ) можно использовать МТИ. Для этого на границе д О располо
жим N граничных узлов в точках с координатами r i , а вокруг области О, на некотором удалении от ее границы, расположим N точечных источника поля с зарядами qj , в точках с координатами Rj . Искомое поле приближенно предста-
вим в виде суммы
U ( r ) = N q j g ( r , R j ) , j = 1
где g ( r, R j ) — фундаментальное решение уравнения Гельмгольца.
В трехмерном варианте
exp ( ±Vx r - R |) g ( r ' R ’ = 14 ,| r - R|
При решении двумерных задач фундаментальные решения [20] выражаются через модифицированные функции Бесселя второго рода (при λ<0):
g (r,R) = K0 (V-^ r - R|)
2n
или через функции Ханкеля нулевого порядка первого рода (при λ>0):
g ( r , R ) = Lh 01 ) (V x | r - R |) .
Знак в (4 1 ) выбирается в зависимости от конкретных особенностей решаемой задачи. В зависимости от знака параметра λ, аргумент экспоненты в выражении (7) будет либо действительным, либо мнимым числом.
При λ=0 уравнение (1) вырождается в уравнение Лапласа, а фундаментальное решение (4 1 ) для трехмерных
задач принимает вид g ( r,R ) = 1/ ( 4n| r
- R |); для двумерных задач в этом случае g ( r, R ) = -^— ln ।—^-^ .
Решение g ( r, R ) можно рассматривать как потенциал поля, созданного в точке r единичным точечным зарядом, находящимся в точке R . При любых значениях зарядов qj функция U ( r ) удовлетворяет уравнению Гельмголь-
ца (1). Необходимо подобрать заряды q таким образом, чтобы граничные условия (2) выполнялись во всех N гранич-
ных узлах. Для узла с номером i условие (2) записывается в виде
N f , d g ( r i, Rj]
X qj a( rj^---- j=1 dn
V
+ P(r)g (ri,j) =y(r).
В результате, записывая уравнение (5) для всех N узлов, получаем систему линейных алгебраических уравнений, систему МТИ. После решения системы (5) искомое поле U ( r ) приближенно находим с помощью формулы
U ( r ) = S q j g ( r, R j ) . (6)
j = 1
Как известно, при некоторых положительных значениях параметра λ краевая задача (1)–(2) для однородного уравнения Гельмгольца при однородных граничных условиях (при у ( r ) = 0) может иметь ненулевое решение. Нахождение значений параметра λ=λ п , собственных значений, соответствующих им решений, собственных функций данной краевой задачи является основной целью данной работы.
При у ( r ) = 0 система МТИ будет представлять собой систему однородных линейных алгебраических уравнений. Как известно, для существования ненулевого решения такой системы необходимо, чтобы ее детерминант равнялся нулю. Однако ошибки округления, возникающие при вычислении детерминанта, приводят к тому, что при приближении параметра λ к некоторому собственному значению наблюдается резкое уменьшение абсолютного значения детерминанта (а не его обращение в ноль) и, соответственно, резкое возрастание числа обусловленности системы МТИ. Это, в свою очередь, ведет к резкому возрастанию погрешности численного решения краевой задачи.
Таким образом, собственные значения краевой задачи можно приближенно установить в процессе получения зависимости от параметра Гельмгольца λ детерминанта или числа обусловленности системы МТИ, или погрешности численного решения краевой задачи. Назовем эти параметры критериями собственных значений.
После того, как собственное значение найдено, можно приступить к нахождению собственных функций, соответствующих данному собственному значению краевой задачи. При этом можно поступить следующим образом. Задается готовое решение U o ( r ) для однородного уравнения Гельмгольца. Таким решением может быть выражение, соответствующее полю точечного заряда Q (4 2 ), расположенного за пределами области решения краевой задачи. Значения этого поля на границе ∂ Ω области Ω используются в качестве правой части в граничном условии (2). Решение краевой задачи, полученное с помощью МТИ, при значении параметра λ, равном одному из собственных значений Х=Х п , можно представить в виде суммы U ( r ) = U 0 ( r ) + u ( r ) , где u ( r ) — собственная функция, собственное решение, соответствующее данному собственному значению. Отсюда следует, что собственная функция будет равняться разности между решением краевой задачи, полученным с помощью МТИ, и заданным решением U 0 ( r ) однородного уравнения Гельмгольца:
u (r ) = U (r ) = Uо (r). (7)
Разумеется, точность такого решения, вследствие плохой обусловленности системы МТИ, может оказаться не очень высокой. Однако, как будет показано ниже, обычно эта точность оказывается вполне приемлемой.
Обычно данному собственному значению краевой задачи соответствует несколько собственных решений. В этом случае возможно нахождение всех собственных решений, соответствующих данному λ п . Для этого описанным выше способом находятся собственные решения, соответствующие различным положениям заряда Q , задающего поле Uo ( r ) . Затем, если это необходимо, между полученными собственными решениями производят ортогонализацию.
Пример нахождения собственных значений для двумерной задачи. В качестве тестового примера рассмотрим нахождение собственных значений и собственных функций задачи Дирихле для однородного уравнения Гельмгольца в круговой области радиусом r 0 . Как известно [21], собственные значения для этой задачи имеют вид
X ^nm, nm 2 ,
-
r 0 2
где цит— положительные корни трансцендентного уравнения Jn ( ц ) = 0 ; Jn ( ц ) — функция Бесселя порядка п, n = 0,1,2,...; m = 1,2,3,... .
Каждому n >0 соответствует две собственные функции:
unm ( r ) = Jn ( r4^nm ) cos n ф , и u™ ( r ) = Jn ( r ^nm ) sin n ф .
При n =0 собственные функции обладают осевой симметрией и равны
u0m (r ) = J0 (r4^0m ) .
При решении тестовой задачи начало координат располагалось в центре круговой области решения радиусом r0=2. Точечные заряды, моделирующие искомое поле с помощью МТИ, равномерно располагались на вспомогатель- ной окружности радиусом R=3. Заряд Q, создающий известное поле U0 (r), располагался на оси Х на расстоянии р=2r0 от центра области О. При нахождении собственных функций и(2) (r) заряд Q перемещается на ось Y.
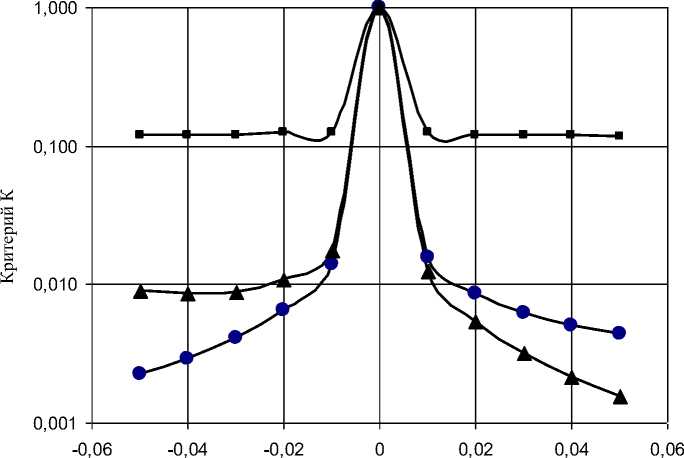
На рис. 1 приведены графики зависимости критериев собственных значений от значения параметра λ. По оси абсцисс откладывается величина (λ–λ 01 )/λ 01 , где λ 01 — наименьшее собственное значение краевой задачи, соответствующее ц 01 -2,405. По оси ординат откладывается либо величина C/C max , где C max — число обусловленности системы МТИ при λ=λ 01 (кривая с квадратными маркерами); либо относительная погрешность ε/ε max , где ε max — погрешность МТИ при λ=λ 01 (кривая с круглыми маркерами); либо величина D min / D , где D min — детерминант (по абсолютной величине) матрицы системы МТИ при λ=λ 01 (кривая с треугольными маркерами). Вычисления проводились при количестве зарядов, моделирующих поле, N =30.
Относительное значение параметра λ
Рис. 1. Зависимости критериев собственных значений от относительной величины параметра λ
Очевидно, что использование зависимости числа обусловленности С от параметра λ для нахождения собственного значения краевой задачи наименее предпочтительно, так как максимум соответствующей кривой слабо выражен (максимальное значение от минимального отличается менее чем в 6 раз). Кроме того, изменение числа обусловленности происходит в очень узком интервале ∆λ значений параметра λ (∆λ≈0,02λ 01 ). Поэтому для нахождения собственного значения краевой задачи целесообразно использовать зависимость погрешности МТИ от параметра λ, так как при этом возможно одновременное нахождение собственных функций.
Следует отметить, что при вычислениях, результаты которых представлены на рис. 1, использовалось число ц 01 -2,405. При подстановке более точного значения этого параметра ц 01 -2,4048255577 максимумы зависимостей, представленных на рис. 1, становятся более резкими. При выполнении тестовой задачи умышленно использовались приближенные значения собственных значений, так как при решении реальных задач, в процессе поиска собственных значений, задается шаг варьирования ∆λ параметра λ, который не может быть бесконечно малым. Реально возможно только приблизиться к собственному значению. При этом собственное значение можно зафиксировать только, если шаг варьирования ∆λ окажется меньше ширины максимума на соответствующей зависимости.
Результаты, представленные на рис. 1, получены при количестве зарядов, моделирующих поле N =30. Вычислительные эксперименты показали, что увеличение количества зарядов N не приводит к существенному улучшению представленных на рис. 1 зависимостей. Более того, максимум зависимости числа обусловленности от параметра λ становится еще менее выраженным. Поэтому при поиске собственных значений рекомендуется использовать небольшое число зарядов, моделирующих поле.
При поиске последующих собственных значений Xnm, с большими значениями п и т, отмеченные выше особенности метода сохраняются с одним существенным дополнением. А именно, чем больше величина собственного значения, тем более узкими становятся соответствующие максимумы на кривых зависимости критериев собственных значений от значения параметра λ. Поэтому, если для поиска λ01, как видно из рис. 1, достаточно задать ширину варь- ирования порядка AX~0,1X01, то при поиске X03, как показали вычисления, шаг варьирования придется уменьшить до значения АХ~О,О2Х03, что, естественно, приведет к увеличению объема вычислений.
Пример нахождения собственных значений для трехмерной задачи. В качестве другого тестового примера рассмотрим нахождение собственных значений задачи Дирихле для однородного уравнения Гельмгольца в кубе со стороной L =2. Для этой задачи собственные значения равны [21]
Xnmk = п2(n2 + m2 + k2)/L2 ; n = 1,2,3,...; m = 1,2,3,...; k = 1,2,3,..., а собственные функции unmk (x, У, z) = sin (nnx / L) sin (nmy / L)sin (nkz / L).
Таким образом, собственные значения определяются величиной числа l = n 2 + m 2 + k 2 . Первому собственному значению с n = 1; m = 1; k = 1; l = 3 соответствует единственное собственное значение. Это собственное значение не вырождено. Следующее по величине собственное значение, соответствующее l = 6 , уже трижды вырождено.
При решении тестовой задачи точечные заряды, моделирующие искомое поле с помощью МТИ, равномерно располагались на поверхности вспомогательного куба со стороной L q =1,3 L . Заряд Q , создающий известное поле UQ ( r ) , располагался на оси Х на расстоянии р= L от центра куба.
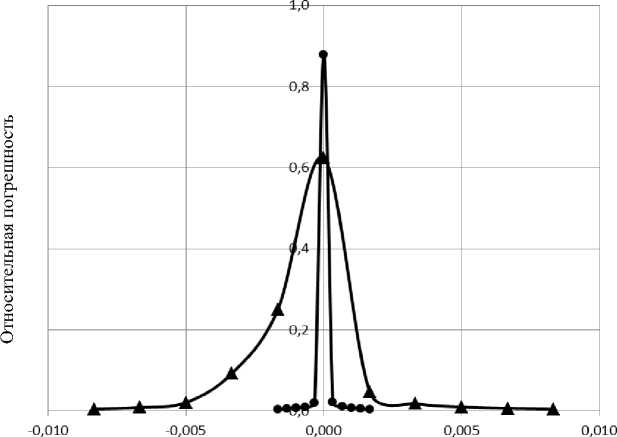
На рис. 2 приведены графики зависимости относительной погрешности МТИ от относительного отклонения параметра Гельмгольца от собственного значения. По оси абсцисс откладывается величина (X-X0)/X0, где Х0 — тестируемое собственное значение краевой задачи. Вычисления проводились при количестве зарядов, моделирующих поле, N =600.
дал.
Рис. 2. Зависимости относительной погрешности МТИ от относительной величины параметра X
На рис. 2 кривая с круглыми маркерами получена для первого по величине собственного значения, при l =3; кривая с треугольнами маркерами — для следующего собственного значения, соответствующего l =6. Как видно из рис. 2, кривая, соответствующая первому собственному значению имеет более резкий и более высокий максимум, чем соответствующая кривая, полученная для второго собственного значения. Для последующих собственных значений максимумы на соответствующих кривых становятся все более размытыми и менее выраженными.
Тестовый пример нахождения собственных функций. После того как собственное значение, например X01, найдено, находится собственная функция краевой задачи (7). При этом необходимо иметь возможность контролировать погрешность получаемого результата. Для оценки погрешности собственной функции u ( r ), полученной с помощью МТИ, сначала производится нормировка этой функции и известной собственной функции (9), путем деления этих функций на их максимальные значения в области решения краевой задачи. После этого оценивается величина е = max u ( r ) - u 01 m ( r ) . r eQ
На рис. 3 приведены зависимости погрешности МТИ для собственных функций от количества зарядов N , моделирующих поле. Приведены зависимости, полученные для λ 01 (кривые с круглыми маркерами), для λ 03 (кривые с треугольными маркерами) и для λ04 (кривые с квадратными маркерами).
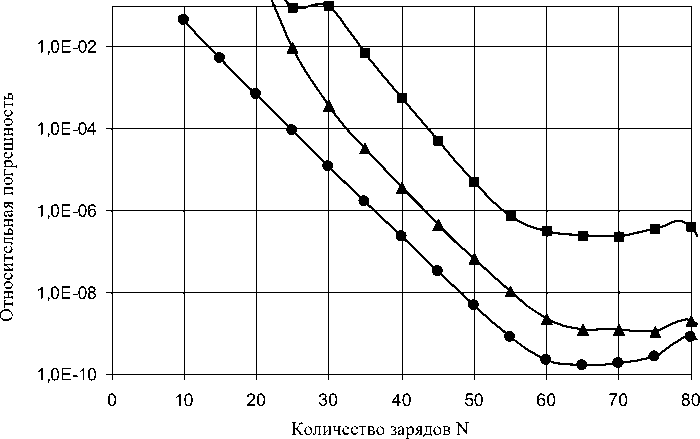
Рис. 3. Зависимости погрешности МТИ для собственных функций от количества зарядов N , моделирующих поле
Как проиллюстрировано на рис. 3, относительные погрешности МТИ для собственных функций оказываются весьма малыми (вплоть до 10-10). Видно также экспоненциально быстрое убывание погрешности с ростом числа зарядов N , характерное для МТИ. Наименьшая погрешность наблюдается при наименьшем собственном значении. Для λ 04 погрешность МТИ оказывается на несколько порядков выше, чем для λ 01 , оставаясь при этом достаточно низкой (порядка 10-6 при N =55).
Как отмечалось выше, собственным значениям λ пт с n >0, соответствуют две собственные функции (8). При вычислении собственных функций (7) с помощью МТИ находится одна из них, либо их линейная комбинация. Это зависит от используемого известного решения U 0 ( r ) , т.е. от положения заряда Q , создающего поле U 0 ( r ) .
На рис. 4 приведен Screenshot с экрана компьютера, на котором приведены графики распределения значений собственных функций вдоль оси Х от центра области решения до ее границы. Параметр λ полагался близким к собственному значению λ12.
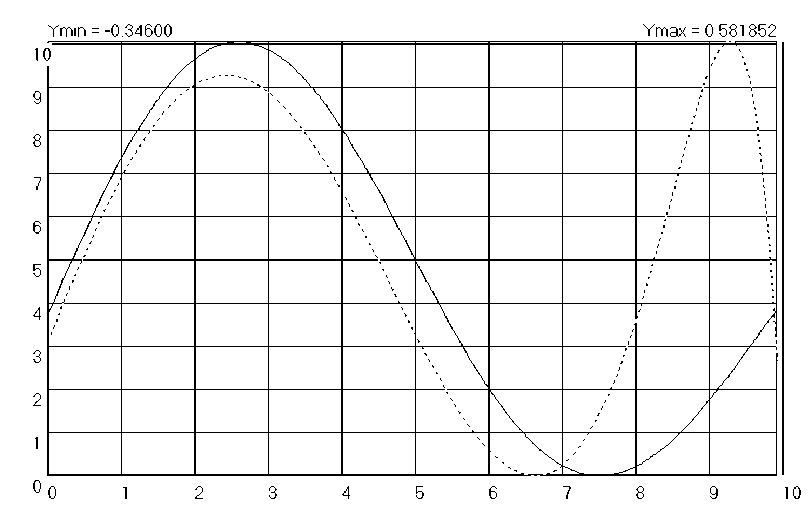
Рис. 4. Screenshot с экрана компьютера, на котором приведены графики распределения значений собственных функций вдоль оси Х от центра области решения до ее границы
Сплошная кривая на рис. 4 соответствует точной величине собственного значения λ 12 . При этом кривая, полученная с помощью МТИ, сливается с графиком аналитического решения и ' 1 ( r ) . Однако небольшое изменение параметра λ приводит к заметному искажению численного решения, как это видно из рис. 4, на котором пунктирная кривая получена при λ=1,01λ 12 .
При моделировании собственных функций, как и ранее, заряд Q , создающий поле U 0 ( r ) , располагался на оси Х на расстоянии р=2 r 0 от центра области О. При этом была получена собственная функция их 2) ( r ) . При переносе заряда Q , создающего поле U 0 ( r ) , на ось Y , моделируется собственная функция u ' 2 ) ( r ) . Это связано с тем, что симметрия собственной функции согласуется с симметрией поля U 0 ( r ) .
При решении трехмерной краевой задачи в объеме куба выбор расположения заряда Q , создающего поле U 0 ( r ) , также определяет ту или иную собственную функцию. Например, для второго собственного значения, при расположении заряда Q на оси X , находится собственная функция u 21i ( x , У , z ) ■ Для нахождения собственной функции м 121 ( x , У , z ) заряда Q необходимо располагать на оси Y , а для функции u n2 ( x , y , z ) — на оси Z .
Заключение. Приведенные выше примеры решения тестовых задач свидетельствуют об эффективности использования МТИ при решении задач на нахождение собственных значений и собственных функций для уравнения Гельмгольца. Учитывая, что при решении этих задач моделирование полей может производиться с помощью небольшого числа точечных зарядов (не более нескольких десятков при решении двумерных задач, нескольких сотен — для трехмерных задач) следует признать этот метод очень экономичным. Трудности, связанные с вырожденностью собственных значений, легко преодолеваются путем использования нескольких различных известных решений U 0 ( r ) , которые не обязательно должны соответствовать полю точечного заряда, но должны согласовываться с симметрией искомой собственной функции.
Список литературы Решение задач на собственные значения для уравнения Гельмгольца методом точечных источников поля
- Fairweather, G. The method of fundamental solutions for elliptic boundary value problems/G. Fairweather, A. Karageorghis//Ad. Vol. Comput. Math. -1998. -Vol. 9. -P. 69-95.
- Alves, C. J. S. A new method of fundamental solutions applied to nonhomogeneous elliptic problems/C. J. S. Alves, C. S. Chen//Advances in Computational Mathematics. -2005. -Vol. 23. -P. 125-142.
- Князев, С. Ю. Устойчивость и сходимость метода точечных источников поля при численном решении краевых задач для уравнения Лапласа/С. Ю. Князев//Изв. вузов. Электромеханика. -2010. -№ 1. -С. 3-12.
- Князев, С. Ю. Численное решение краевых задач для уравнения Пуассона методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. А. Енгибарян//Вестник Дон. гос. техн. ун-та. -2014. -Т. 14., № 2 (77). -С. 15-20.
- Князев, С. Ю. Решение трехмерных краевых задач для уравнений Лапласа с помощью метода дискретных источников поля/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2015. -№ 5. -С. 25-30.
- Бахвалов, Ю. А. Погрешность метода точечных источников при моделировании потенциальных полей в областях с различной конфигурацией/Ю. А. Бахвалов, С. Ю. Князев, А. А. Щербаков, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2012. -№ 5. -С. 17-21.
- Князев, С. Ю. Сравнительный анализ двух вариантов метода коллокаций при численном моделировании потенциальных полей/С. Ю. Князев, Е. Е. Щербакова, А. Н. Заиченко//Известия высших учебных заведений. Электромеханика. -2014. -№ 1. -С. 17-19.
- Князев, С. Ю. Решение задач тепло и массопереноса с помощью метода точечных источников поля/С. Ю. Князев, Е.Е. Щербакова//Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. -2006. -№ 4. -С. 43-47.
- Князев, С. Ю. Моделирование полей упругих деформаций с применением метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15., № 1 (80). -С. 29-38.
- Князев, С. Ю. Моделирование трехмерных полей упругих деформаций с помощью метода точечных источников/С. Ю. Князев, В. Н. Пустовойт, Е. Е. Щербакова, А. А. Щербаков//Вестник Дон. гос. техн. ун-та. -2015. -Т. 15., № 4 (83). -С. 13-23.
- Князев, С. Ю. Сравнительный анализ различных вариантов использования метода точечных источников поля при моделировании температурных полей/С. Ю. Князев, Е. Е. Щербакова, А. А. Щербаков//Физико-математическое моделирование систем: материалы XII междунар. семинара. -Воронеж, 2014. -С. 52-56.
- Лунин, Л. С. Исследование стабильности термомиграции ансамбля линейных зон с помощью трехмерной компьютерной модели, построенной на основе метода точечных источников поля/Л. С. Лунин, С. Ю. Князев, Б. М. Середин, А. С. Полухин, Е. Е. Щербакова//Вестник Южного научного центра. -2015. -Т. 11, № 4. -С. 9-15.
- Князев, С. Ю. Математическое моделирование полей упругих деформаций методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. А. Щербаков//Математические методы в технике и технологиях. -2015. -№ 5 (75). -С. 21-23.
- Князев, С. Ю. Компьютерное моделирование потенциальных полей методом точечных источников/С. Ю. Князев, Е. Е. Щербакова, А. А. Щербаков. -Ростов-на-Дону: Издательский центр ДГТУ, 2012. -156 с.
- Князев, С. Ю. Метод точечных источников для компьютерного моделирования физических полей в задачах с подвижными границами: дис. …доктора техн. наук/С. Ю. Князев. -Новочеркасск, 2011. -342 с.
- Князев, С. Ю. Численное исследование стабильности термомиграции плоских зон/С. Ю. Князев, Е. Е. Щербакова//Известия высших учебных заведений. Электромеханика. -2007. -№ 1. -С. 14-19.
- Бахвалов, Ю. А. Математическое моделирование физических полей методом точечных источников/Ю. А. Бахвалов, С. Ю. Князев, А. А. Щербаков//Известия Российской академии наук. Серия физическая. -2008. -Т. 72., № 9. -С. 1259-1261.
- Князев, С. Ю. Численное решение уравнений Пуассона и Гельмгольца с помощью метода точечных источников/С. Ю. Князев//Известия высших учебных заведений. Электромеханика. -2007. -№ 2. -С. 77-78.
- Князев, С. Ю. Численное решение краевых задач для неоднородных уравнений Гельмгольца методом точечных источников поля/С. Ю. Князев, Е. Е. Щербакова, А. Н. Заиченко//Известия высших учебных заведений. Электромеханика. -2014. -№ 4. -С. 14-19.
- Абрамовиц, А. Справочник по специальным функциям/А. Абрамовиц, И. Стиган. -Москва: Наука, 1979. -832 с.
- Полянин, А. Д. Справочник по линейным уравнениям математической физики/А. Д. Полянин. -Москва: Физматлит, 2001. -576 с.


