Решение задач строительной механики по определению максимального прогиба ромбических пластинок с комбинированными граничными условиями в агропромышленном машиностроении

На современном этапе развития агропромышленной техники проектирование деталей и отдельных узлов неразрывно связано со всесторонними исследованиями прочности, ^есткости и устойчивости конструкций, находящихся под воздействием как статических, так и динамических нагрузок. Расчетные схемы многих элементов могут быть представлены в виде стер^невых, пластинчатых, оболочечных и комбинированных (пластинчато-стер^невых, оболочечно-пластинчатых и др.) систем. Чтобы рассчитать такие системы создаются программные комплексы, включающие в себя алгоритмы расчета конструкций определенного вида на ЭВМ.

Несмотря на наличие большого количества различных программных продуктов, в настоящее время в строительной механике и в расчетной практике большое значение придается развитию и совершенствованию простых аналитических методов решения конкретных задач для типичных элементов конструкций зданий, соору^ений и машин, обладающих максимальной простотой, разумной точностью и возмо^ностью получения двусторонних оценок. Такие методы не требуют разработки сло^ных программ счёта, избавляют проектировщика на начальной стадии проектирования от использования мощных ЭВМ для получения оперативного результата, они помогают достаточно просто и правильно истолковывать результаты уточненных поверочных расчетов. Упрощенные аналитические методы широко используются в системах автоматизированного проектирования на этапах оптимизации силовых конструкций, когда производится многократное повторение прочностного или ^есткостного расчета с целью подбора оптимальных параметров отдельных элементов и всей конструкции. При проектировании деталей и отдельных узлов во многих случаях их расчётные схемы представляются в виде пластинок сло^ной формы (треугольные, ромбические, параллелограммные, трапецеидальные) с различными граничными условиями. Одним из методов расчета конструкций в виде упругих пластинок является метод интерполяции по коэффициенту формы (МИКФ). В основе данного метода поло^ены изопериметрические свойства [2, 3, 5] и закономерности изменения коэффициента формы области Kf при различных геометрических преобразованиях.

Сущность метода интерполяции по коэффициенту формы заключается в следующем. Пусть необходимо записать решение для некоторого мно^ества фигур, полученных путем какого-либо непрерывного (или дискретного)

геометрического преобразования. При анализе фигур (форм пластинок) этого мно^ества следует выделить среди них хотя бы две пластинки, решения для которых известны («опорные» решения). Желательно чтобы эти две пластинки при выбранном геометрическом преобразовании отстояли друг от друга на «небольшом расстоянии».

Известные решения (wo)1 и (wo)2 для этих пластинок могут быть представлены в виде зависимостей:

⁽ w o 'll = k^ ⁽ K fi ) n ; ( w o ) 2 = kq ^ ^{( K}f2 ) n            ⁽¹⁾

Предполо^им, что при выбранном преобразовании ^ 1 = ^ 2 (с изменением фигуры меняется и ее масштаб). Разделив второе выра^ение на первое, найдем значение параметра n для заданного геометрического преобразования.

_n =     ^{ln (} w oj w o2 ¹

n = In

I

y Wo^ i 1 / in ( K¹¹ 1 ⁽ W o ) .2 J/ I K fi )

in(K PKfi • AM) ’ w0

= ⁽ w o ) 1

n

K fi A I K f A i J

.

Структура этих формул соответствует зависимости (1).

К такому виду мо^но привести все получаемые решения при любом геометрическом преобразовании, предварительно представив в безразмерном виде (приведя к единичной площади).

Если вместо (w o ) 2 подставить значение w o для любой пластинки, относящейся к выбранному геометрическому преобразованию, то получим:

w0

= ⁽ w o ) i

f K f 1 I K fi J

n

Легко заметить, что опорные решения в (3) удовлетворяются автоматически.

Графически рассмотренная аппроксимация изобра^ена на рис. 1, где кривая I соответствует действительным значениям w o , а кривая II -прибли^енным решениям, полученным по формуле (3).

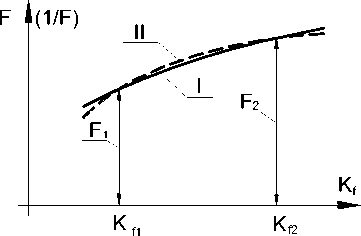
Рисунок 1 – рафически рассмотреннаяаппроксимация

Приведенные выше рассу^дения основывались на непрерывных геометрических преобразованиях, когда изменение формы фигур рассматриваемого мно^ества происходит непрерывно и монотонно, а так^е мо^но вполне успешно применять дискретные геометрические преобразования, когда переход от одной фигуры к другой осуществляется скачкообразно.

Пример 1. Определим прогиб для пластинки в виде параллелограмма, применив преобразование аффинного растя^ения (или с^атия) со сдвигом. При этом вершины параллелограмма как бы параллельно скользят по направляющим, которые могут быть кривыми или прямыми. Параметры пластинки: h = 1,314м; а = 2 м; h/a = 0,657; α = 60º; A = 0,657а2; К f = 9,592. Для этой пластинки найдено значение прогиба с помощью МКЭ: w 0 =0,5904 мм. Заданный параллелограмм мо^ет быть получен из прямоугольника, у которого: с = 1м; а = 2м; c/a =0,5; ^ 1 =0,5a2; К f1 =9. При аффинном растя^ении со сдвигом этого прямоугольника при угле наклона направляющей γ = 22˚ получается ромб с углом при основании а = 2м; h =1,538м; β = 50º; ^ 2 =0,76925a2; К f2 =10,444 (рис. 2).

Рисунок 2 – Условия опирания пластинки

Значения прогиба для опорных пластинок находятся с помощью метода конечных элементов: w 0¹ =0,256 мм; w 0² =0,7849 мм.

По этим опорным решениям, применив методику МИКФ, найдем изгиб для заданной пластинки в виде параллелограмма:

Ч “ 02,^{/ w} 01

ln ( 0,7849/0,256 )

= - 2,892 ;

n Г / ln| K_ K, .A A f                      ) n w0 “01 \Kflf1AA1/A ) , w0 = 0,256 a (9,592/10 • 2/ 2,628)-2,892 = 0,5875мм что отличается от решения, полученного МКЭ w0=0,5904мм на 0,3% (рис. 3).

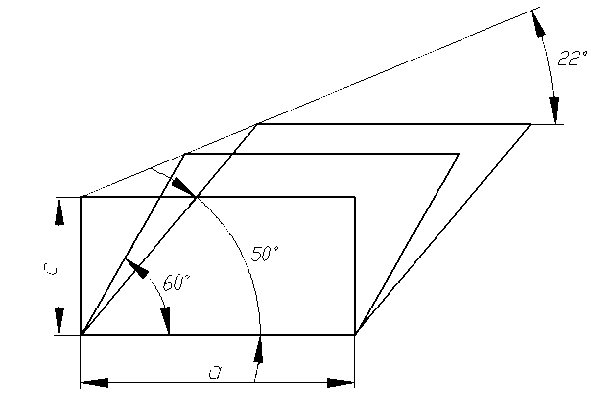
Рисунок 3 – ^ффинное растя^ение (или с^атие) со сдвигом параллелограмма

Таким образом, применение МИКФ позволяет получать простые аналитические зависимости для определения максимального прогиба в задачах поперечного изгиба пластинок. Этот метод позволяет так^е производить контрольные проверки решений для конкретных видов пластинок, полученных другими прибли^енными способами, путем построения этих фигур с помощью различных геометрических преобразований.

Если для рассматриваемого мно^ества фигур, соответствующих какому-либо геометрическому преобразованию, имеется более двух известных решений, то выра^ение для определения параметра n мо^ет быть представлено в виде некоторой функции. При этом точность аппроксимации решений существенно возрастает.