Решение задач жесткого плоского нагружения в рамках эндохронной теории неупругости для больших деформаций и поворотов

Геометрически нелинейные теории неупругости достаточно давно и весьма подробно изучаются исследователями [1-5]. Классическая эндохронная теория Валаниса, естественно, тоже имеет ряд вариантов, учитывающих большие деформации [6-7]. В [8] были сформулированы основные принципы учета больших деформаций и поворотов в эндохронной теории тензорно-параметрического типа. Наиболее полный набор вариантов определяющих соотношений этой теории можно найти в [9]. В [10-11] опубликованы некоторые результаты, полученные в рамках эндохронной теории тензорно-параметрического типа, учитывающей большие деформации и повороты, на простых и сложных путях нагружения. В предлагаемой статье представлена подробная схема решения определяющих уравнений неупругого поведения материалов на плоских жестких путях нагружения.

1.    Определяющие соотношения теории неупругости эндохронного типа

Рассматривается вариант эндохронной теории неупругости тензорно-параметрического типа для больших деформаций и поворотов [9] в виде

О

I *1 °         ° r r + ат =----

¹¹ 2 G    2 G g + а

* ОО                °

I r | +Т r , 8 = D , 8 q = -° , K

*

, °    * *         . °    О r = 8-(1 -а)—, r = 8-(1 "а)—, r = D-(1 ‘Отут, 2 G           2G2

*

^т = ^{т (} I r l, I r l X I r I

J^ dr : dr ,

*

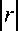
dr dr dt dt

Здесь в безындексной форме записи тензоров т - аналог деформационного предела текучести, g - аналог коэффициента упрочнения, G - модуль сдвига, K - объемный модуль, a - параметр эндохронности, 0 < а <  1, 8 ₀ = 8 ii , ° ₀ = a ii , r - девиатор вспомогательного параметри-

О О ческого тензора. Объективные производные ° и 8 девиатора тензора напряжений Коши о и девиатора тензора деформаций 8 определяются формулами типа Грина-Нахди:

О *

О *

° = °+°О-О° , 8 = 8 + 80-08 ,

*

где О = QQ^T - тензор вихря, Q - ортогональный тензор поворота в полярном разложении F = QU градиента деформации F . Кроме того, U -

*

правый тензор удлинения, L = FF

^^^^в

1 - градиент скорости деформации,

D = ( L + L ) ^2 - тензор скорости деформации, причем U ² = F T F и Q = FU ^-1.

Второе соотношение в (2) фактически определяет меру деформации, автоматически порождаемую нейтральной коротационной производной Грина-Нахди при преобразованиях вращения в форме s = Q^ QTDQ) dt QT.

Отметим, что деформации (3) отличаются от мер деформаций, входящих в классификацию Хилла в = (Uⁿ - I )/ и , n = 0,1,2, I - единичный тензор. Этот факт, по-видимому, был впервые четко отмечен в [12]. Различие мер деформации следует учитывать при сравнении расчетов по теории (1) с результатами других исследований.

2.    Порядок решения задач

Плоским жестким будем называть зор скорости деформации в виде нагружение, когда задан тен-

D =

( D 1

D

D 1 D

I 0

л

.

Тогда, если рассматривать минимальный набор компонент тензора градиента деформации

	к11	k 12	0 )
F =	0	k 22	0
	. 0	0	1V

, который может породить тензор скорости деформации типа (4), то, пользуясь определениями градиента скорости деформации L и тензора скорости деформации D, нетрудно получить дифференциальные соотношения, связывающие компоненты тензоров F и D:

• •                       •       ••

п _ к 11   п _ к11 к 12 - к 11 к12

D , D                   , D??

11             1222

k11             2 k11 k22

Решая дифференциальные уравнения (6) с заданными компонентами D ij при естественных начальных условиях к 11 (0) = 1, к ₂₂ (0) = 1 и к ₁₂(0) = 1, можно вычислить компоненты градиента деформации (5).

Найденный тензор градиента деформации позволяет вычислить ортогональный тензор поворота Q по схеме, предложенной в [13]. Так как любой кососимметрический тензор K связан с ортогональным тензором поворота Q соотношением [13]

Q — I+Sinto к + k2oSto к 2, to            to2

где

			22
' 0	-to 3 to 2 '		-to 3 — to 2      to 1 to 2	to 1 to 3
к —  to 3	0 -to 1 , к 2 —		22 to 1 to 2      —to 1 — to 3	to 2 to 3
<-to 2	to 1       0 J		to 1 to 3          to 2 to 3	2     2 —to 2 — to 1
		V		7

222 to — ^ toi + to2 + tog ,

то, построив кососимметрический тензор, определим для найденного F вид ортогонального тензора поворота Q .

Отметим, что способ нахождения тензора K в работе [13] не указан. Рекомендуется использовать следующий вариант построения кососимметрического тензора:

K — ( F — F^T )/2.                         (8)

Эта формула в общем случае определяет число независимых параметров тензора поворота Q . Количество параметров может иметь значение 1, 2 или 3.

Для рассматриваемого класса жестких нагружений (4) тензор Q имеет один свободный параметр, то есть

	2 cos P	sin P	0 )
Q —	— sin P	cos P	0
	v 0	0	1 J

Для конкретизации связи параметра р с историей нагружения необходимо использовать условие симметрии вычисленного по (9) правого тензора удлинения U — Q ^{— 1} F — Q T F . Затем определяется тензор

• вихря О — QQT. Например, для тензора Q в форме (9) получаем

•	Г 0	1	0 )
О=р	- 1	0	0
	. 0	0	0 J

Предполагая, что тензоры напряжений и деформаций имеют вид

	Г° 11	о 12	о 13 ^		Г£ 11	£ 12	£ 13 ^
о -	° 21	о 22	о 23	и £-	£ 21	£ 22	£ 23	,            (11)
	v° 31	о 32	о зз ;		<£ 31	£ 32	£ 33 >

подставим их в определяющие соотношения (1)-(2) при 2 G — 1 и а - 1 и получим рабочие определяющие уравнения в форме

о 11 - 2 о ₁₂ P + D 11 - m о_п + km £ 11

⁰ 22 ^{- 2 о} 12 ^{р +} D 22 ^- m ^о 22 ⁺ km ^£ 22

⁰ 12 ^-0 21 ^{- P ( о} 11 ^-о 22 ) ⁺ D 12 ^- m ^о 12 ⁺ km ^£ 12 ,

<

•

^£ 11 ^{— 2 £} 12 P ⁺ D 11 ,

•

^£ 22 ^{— - 2 £} 12 P ⁺ D 22 ,

•

^£ 12 ^{- £} 21 ^{- -P} ( ^£ 11

•

^^^^^^^в

^£ 22 ) ⁺ D 12 ,

k 11 - k 11 D 11 , k 22 ^- k 22 D 22 ,

. k 12 - 2 k 22 D 12 + k 12 D 11 -

Здесь приняты следующие обозначения:

k = ^т, m - —, I £ \ =М1 +£ 22 + 2 £ 22 .

g + 1 т ^v

Остальные компоненты тензоров напряжений и деформаций равны нулю. Дополнительно (для наглядности вычислений) предполагалось, что тензоры (4) и (11) девиаторы.

3. Частные случаи и примеры

Задавая компоненты тензора скорости деформации (4), можно реализовать различные схемы жесткого нагружения. В частности, если компоненты тензора (4) - константы, то, например:

а) при D ₁₁ = 0, D ₂₂ = 0, D ₁₂ = 1 реализуется простой сдвиг ( М -нагрузка). В этом случае решение уравнений (6) дает

	7 1	2 t	0 )
F =	0	1	0
	V 0	0	1 1

,

•         1

а схема (7)-(8) приводит к (9) и (10) с параметром р в форме р =----;

1 + t ²

б) для D ₁₁ Здесь получаем

= ¹ D 22

= 0,

D 12 = 0 - растяжение ( Р - нагрузка).

F =

e

V

et

и

•

р=

e^t _;

( e t )² + (1 + e t )² ;

в) если D ₁₁ =

- 1, D ₂₂ = 0, D ₁₂ = 0 - сжатие ( Р - нагрузка), тогда

F =

7 - 1 e

V

- t

e

и

•

р=

- e t

( e ^- t )² + (1 + e ^- t )² ’

г) при D ₁₁ = 0,

^D 22

= 1,

D 12 = 0 имеем аналог внутреннего давле-

ния (р - нагрузка). Для этого варианта жесткого нагружения оказывается, что

0 ^

F =

V

et

и

•

р=

- et      .

1 + (1 + e t )^{2 ;}

д) для D ₁₁ = q , D 22 = 0,

D ₁₂ = 1 - пропорциональное нагружение

( Р-М -нагрузка). Для этого случая получаем

^ eq q2(eq -1) 0 ^ F = 0 1 0 и 0 0 1 V 7 р =----^--

(eq +1)2 + -42 (eq q2

^^^^^^^в

; 1)2

• е) если D 11 = 1, D 22 = 1, D 12 = 1 - общее плоское нагружение с постоянной «скоростью деформации» ( Р-М-р - нагрузка), тогда имеем

  	( e t e t (2 1 + 1) 0 )
  F =	0       e t      0	и ₽ =     1 V
  	0      0      1	1    - - 1 1 2
  	\                 J	I 2 J

Нетрудно по аналогии с пунктами а)-е) реализовать переменные, сложные и циклические нагружения. Например:

D 11 = + const, D 22 = 0, D 12 = 0 - циклическое растяжение-сжатие;

D11 - 0, D22 = 0, D12 - A sin(wt) - аналог периодически изменяющейся скорости деформации кручения;

D = 1

' D_n = 1, D 22 = 0, D 12 = 0, t <  1 0 , _ D 11 = 0, D 22 = 0, D 12 = 1, t >  1 0

аналог сложного нагружения

под углом 90 градусов в пространстве скоростей деформации (в терминах теорий малых неупругих деформаций).

На рис. 1, 2, 3, 4, 5, 6 приведены графики развития деформаций и напряжений в зависимости от параметра нагружения для простого сдвига (случай а), растяжения (вариант б), сжатия (схема в), «внутреннего давления» (случай г), пропорционального нагружения под углом 45° (вариант д и q = 1) и общего плоского нагружения (схема е) соответственно. Расчеты проведены при параметрах материала т = 1 и к = 0,1.

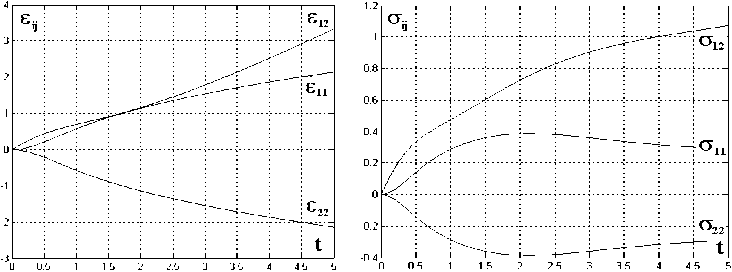
Рис. 1. Развитие деформаций и напряжений при простом сдвиге

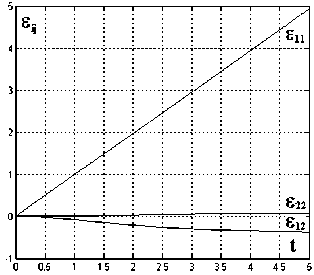
Рис. 2. Поведение деформаций и напряжений при растяжении

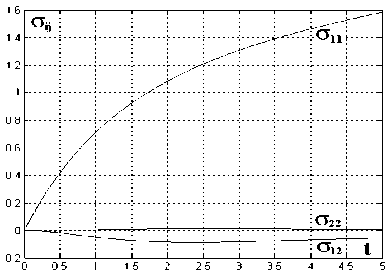
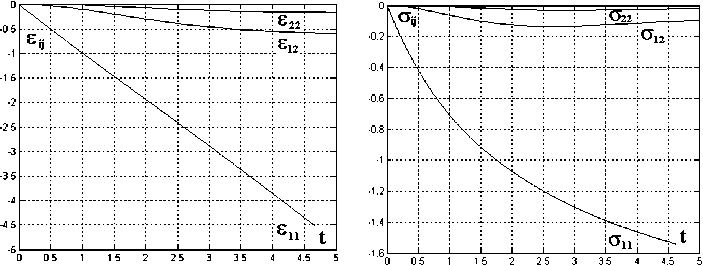
Рис. 3. Деформации и напряжения при сжатии

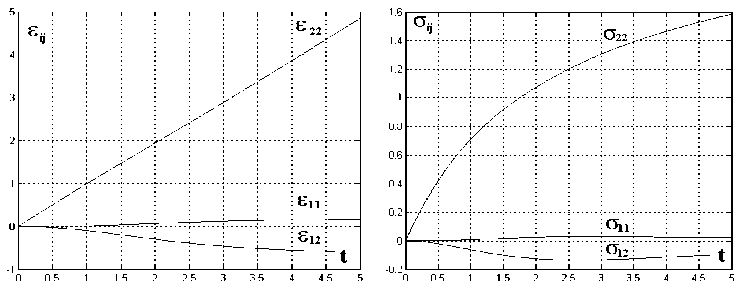
Рис. 4. Зависимость деформаций и напряжений от параметра нагружения при «внутреннем давлении»

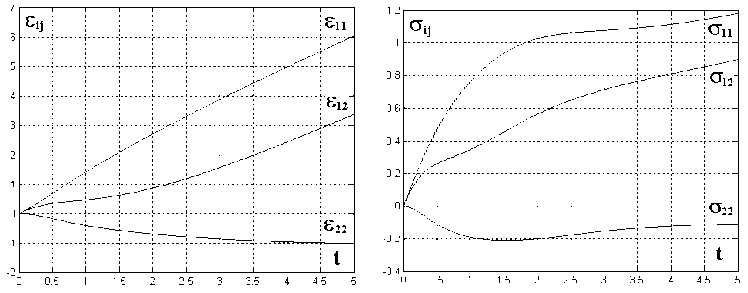
Рис. 5. Развитие деформаций и напряжений при пропорциональном нагружении под углом 45 градусов

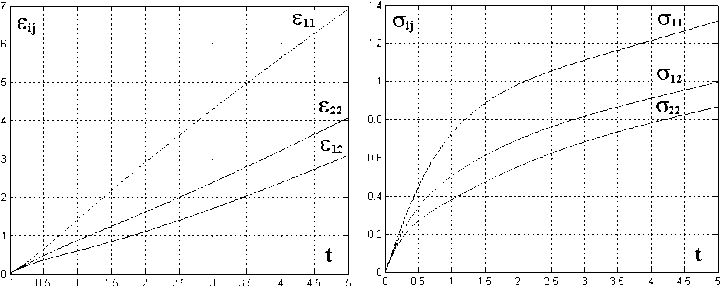
Рис. 6. Деформации и напряжения в общем плоском нагружении

Отметим монотонный характер развития всех компонент деформации и напряжения на рассматриваемых путях деформирования, появление осевых деформаций при простом сдвиге и сдвиговых деформаций при растяжении, сжатии и «внутреннем» давлении. Следует обратить внимание и на более высокий уровень сдвиговых напряжений о_п по сравнению с напряжением ^ 22 в общем плоском случае нагружения.

На рис. 7 приведены графики развития интенсивности напряжений от интенсивности деформаций для всех рассмотренных случаев. Очевидна зависимость от вида напряженного состояния, что не может быть получено в геометрически линейных вариантах теории.

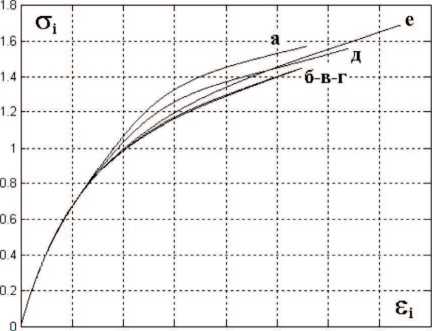
0       1       2       3       4       5       6       7       8

Рис. 7. Зависимость интенсивности напряжений от интенсивности деформаций

Таким образом, приведенные выше примеры показывают, что при жестком плоском нагружении предлагаемый вариант эндохронной теории неупругости (1)-(2) способен описывать основные (и некоторые тонкие) эффекты поведения материалов, отмеченные экспериментаторами [14-15]. Отметим и новый четкий порядок производства вычислений по схеме (4)-(8).

Работа выполнена при финансовой поддержке РФФИ (грант № 10-01-00705).