Решение задачи аэроупругости в переменных метода конечных элементов (МКЭ)

Современные средства проектирования летательных аппаратов (ЛА) предполагают обязательное создание конечно-элементной (КЭ) модели, на которой решается задача статической прочности ЛА. Однако для решения задач аэроупругости традиционно создаются упрощенные, пластинно-балочные расчетные модели ЛА. Не оспаривая таких преимуществ, как вычислительная эффективность и физическая ясность данных моделей, следует отметить, что пластинно-балочные модели не являются конструктивно-подобными, а это требует дополнительной работы по их инициализации, а затем по переносу получаемых результатов на проектируемую конструкцию. Поэтому вполне естественна попытка, оставаясь в рамках КЭ модели, решить задачу аэроупругости. Тем более что необходимая для этого массовая модель ЛА также строится на базе МКЭ.

Однако расчет аэродинамических нагрузок, используемых в задачах аэроупругости, производится на аэродинамической модели, и возникает необходимость передачи аэродинамических нагрузок на КЭ модель. Другой проблемой является высокий порядок и заполненность получаемых при этом аэродинамических матриц, что влечет за собой потребность в значительных объемах оперативной памяти для их размещения и больших ресурсах процессора для их обработки.

В настоящей статье рассматриваются пути преодоления этих трудностей с тем, чтобы вычислить критическую скорость флаттера/дивергенции агрегатов ЛА на базе его КЭ модели. Постановка задачи расчета на флаттер/дивергенцию на базе МКЭ подразумевает запись уравнений вынужденных колебаний ЛА (или его агрегата) в узловых перемещениях КЭ модели. Возбуждающими силами при этом выступают аэродинамические силы. В матричной записи имеем:

M tin + Dqn + Kqn = Qn, (1) где qn– вектор узловых перемещений; Qn– вектор аэродинамических узловых сил; m , d и k– матрицы массы, демпфирования и жесткости КЭ модели соответственно, а точка означает дифференцирование по времени. Следует отметить, что матрица массы должна отражать реальное распределение массы (в т.ч. несиловой) конструкции. Эле- менты матрицы D , соответствующие конструкционному демпфированию, имеют малый порядок в сравнении с таковыми для аэродинамического (см. далее) демпфирования и в учет не принимаются. Если же КЭ модель охватывает и систему управления, то вопрос о включении соответствующих элементов в матрицу D решается специально.

Определение полного вектора перемещений q_n конструкции на основании (1) является весьма трудоемкой задачей ввиду высокой размерности КЭ модели ЛА и заполненности аэродинамических матриц, связывающих вектор Q_n с векторами q_n и q_n . Однако описание движения агрегатов ЛА через q_n является избыточным. Пространственная часть q_n может быть приближенно представлена как суперпозиция некоторого набора заданных координатных векторов Ф _k , например, собственных форм колебаний ЛА [1]. Временна́я зависимость q_n представляется скалярными функциями ф _k ( t ) . Таким образом, выполняется разложение:

Q n = Е ^Ф k ф k ^{( t} ) =^фф. ⁽²⁾ k

Собственная форма Ф k есть решение уравнения свободных колебаний с собственной часто- той tok:

го ^ М Ф _k = К Ф _k .

Собственные частоты находятся из уравнения:

|го2М - К| = 0.

Для повышения устойчивости алгоритмов, использующих собственные формы, последние подвергают ортогонализации и нормировке:

f i

о

ф T Ф j =

i = j i * J

Использование в качестве заданных функций

Ф _k собственных форм колебаний КЭ модели имеет свои преимущества: во-первых, собственные формы отражают распределение жесткостей и масс конструкции, что облегчает задачу правильного выбора диапазона форм, по которым производится разложение (2); во-вторых, ввиду ортогональности собственных форм ряд (2) сходится быстрее.

Для определения аэродинамических нагрузок строится аэродинамическая модель, соответствующая рассматриваемой конструкции. В результате аэродинамического расчета устанавливается связь аэродинамических нагрузок с величиной и скоростью деформирования конструкции. Например, при использовании панельного метода вычисляются производные коэффициентов давления в контрольных точках аэродинамических панелей по углам атаки этих панелей в виде матрицы аэродинамического влияния. Аэродинамические силы, действующие на панели, приложены в контрольных точках [2]. Возникает необходимость приведения системы аэродинамических сил, действующих в контрольных точках, к силам, действующим в узлах КЭ модели. Так как явления аэроупругости связаны с переходом энергии воздушного потока в энергию колебаний конструкции, в качестве принципа эквивалентности двух систем сил, естественно использовать условие равенства виртуальных работ, выполняемых каждой такой системой:

( § Q n ) ^TQ n = ( § Q a ) ^TQ a , (3) где q_a – вектор перемещений контрольных точек, Q_a – вектор аэродинамических сил, действующих в контрольных точках. Строго говоря, аэродинамические панели могут не иметь общих точек с конечными элементами и, поэтому каждой контрольной точке поставим в соответствие некоторую точку конечного элемента, исходя из следующих соображений. Аэродинамические силы передаем только на 2D элементы КЭ модели. Аэродинамическая сила действует в контрольной точке по нормали к аэродинамической панели. Если нормали к конечному элементу и к аэродинамической панели параллельны, причем аэродинамическая нормаль «прошивает» конечный элемент, то точку ее пересечения с конечным элементом используем как альтернативу аэродинамической контрольной точке, т.е. параллельно переносим в нее вектор аэродинамической силы. Если таких «прошитых» аэродинамической нормалью конечных элементов окажется несколько, то выбираем ближайший к контрольной точке (расстояние измеряется вдоль нормали). Очевидно, что характер аэродинамического нагружения конструкции при этом практически не изменится. Более того, условие параллельности нормалей можно даже ослабить, допустив небольшой угол между ними. Таким образом, условие (3) будет теперь пониматься как равенство виртуальных работ аэродинамических сил, приложенных к конечным элементам в точках, альтернативных контрольным (далее – новых контрольных точках) и узловых сил. Перемещения новых контрольных точек, как внутренних точек конечных элементов, выражаются через узловые перемещения КЭ модели стандартным для МКЭ способом [1]:

5 q_a = H 5 Q n , (4)

где h – интерполяционная матрица. Подставляя (4) в (3) и применяя правило транспонирования произведения матриц, получим:

(SQn )TQn = (SQn )THTQa, откуда следует уравнение связи векторов узловых и аэродинамических сил:

Q n = H^TQ_a . (5)

Очевидно, что увеличение размерностей КЭ и аэродинамической моделей ЛА приводит к уменьшению погрешностей, обусловленных сделанными допущениями.

Полные углы атаки а и скольжения р аэродинамической панели в контрольной точке определяются пространственной ориентацией ближайше- го к панели конечного элемента из числа «прошитых» аэродинамической нормалью и проекциями скорости новой контрольной точки на оси OY и OZ системы координат:

д v 1 dv     o     дw   1 dw a =-----, P= —~--777^, дx V дt          дx  V д t где v и w – перемещения новой контрольной точки по осям OY и OZ соответственно, V – скорость потока (параллельна оси OX). Вектор аэродинамических сил в контрольных точках определяется матрицами аэродинамического влияния C и пло- щадей панелей s :

nA

Q a = ¹ P V 2 SC              (7)

²       \PJ

Матрица аэродинамического влияния C содержит подматрицы порядка 2х2 перекрестных производных по углам а и в коэффициентов аэ- родинамических сил, действующих по осям OY и OZ в контрольной точке каждой аэродинамической панели:

[ С ] =

α C_y

C^α z

_Cβ _y C^β

Матрица площадей панелей S – диагональная, содержит подматрицы порядка 2х2 с дважды повторяющейся площадью каждой панели:

[ S ] =

S0

0S

Вектор обобщенных перемещений новых контрольных точек определяется через их осевые пе- ремещения как

Г и )

qa

v

( w J

Учитывая (10) в (6), а также (5) и (7), получим вектор узловых аэродинамических сил:

Qn = -1 pV2HTSCHXqn -1 pVHTSCHqn.

После введения в (11) обозначений:

B = 1 pHTSCH‘ , D = 1 pHTSCH ,(12)

перепишем (1) с учетом (11) и (12):

M qn + VDqn + (K + V2B)qn = 0.(13)

Входящие в (13) матрицы B и D именуемые как «матрица аэродинамической жесткости» и «матрица аэродинамического демпфирования», соответственно, являются заполненными и несимметричными, что вместе с высоким порядком системы (13) делает ее решение весьма затруднительным.

Принимая во внимание соображения, сопутствующие представлению (2), выполним редуцирование системы (13) по k собственным формам.

Для этого подставим (2) в (13) и умножим (13) слева на Ф ^T . В результате получим систему уравнений порядка k«n относительно новых переменных ф :

M ф + VD ф + (K + V 2 B) ф = 0 ,      (14)

где

M =ф ^ТМ Ф ; K = Ф ^ТК Ф ; B =Ф ^TB Ф ; D =Ф ^TD Ф .

Определение границы флаттера по скорости производится на основании анализа корней системы (14) [4]. Для получения характеристического уравнения ищем решение (14) в виде:

ф = AeXt, и приравниваем нулю определитель:

I X ²M +X VD + (K + V²B)| = 0 .     (15)

В силу того, что коэффициенты (15) действительные, решения X могут быть действительными и/или комплексно-сопряженными. Для асимптотической устойчивости системы (14) необходимо и достаточно [5], чтобы вещественные части всех корней характеристического уравнения (15) были отрицательны: Re X m ( 0 , m = 1,k . Если существует s e( 1,k ) такое, что Re X _s ) 0 — система является неустойчивой. Таким образом, граница флаттера по скорости задается условиями:

f Re X (V) = 0

,                       (16)

[ Im X (V) * 0

а дивергенции:

f Re X (V) = 0

.                     (17)

[ Im X (V) = 0

Следует отметить, что скорость V входит в (15) явно, как полином, и неявно, через матрицы B и D , которые, согласно (12), получены для определенной матрицы влияния C , также зависящей от скорости (точнее от числа Маха). Поэтому для определения критической скорости флаттера/дивер-генции необходим двухуровневый итерационный алгоритм: внутренний цикл – решает систему (16,17) при фиксированных B и D , внешний – сравнивает полученную скорость с той, при которой вычислялась C , и при необходимости, вычисляет C повторно для новой скорости.

Изложенная методика определения критической скорости флаттера/дивергенции реализована в виде программного модуля для ПК. Численные эксперименты показали ее эффективность и универсальность.

В качестве примера выбрано цельноповоротное горизонтальное оперение (ГО) сверхзвукового ЛА, для которого проведено экспериментальное определение частот собственных колебаний ГО на фюзеляже, а также взвешивание консоли ГО.

Для ГО были созданы КЭ, массовая и аэродинамическая модели.

КЭ модель ГО (рис. 1) создана в программном комплексе ОТСЕК [6]. В КЭ модели ГО использованы три типа конечных элементов: трех- и четы-

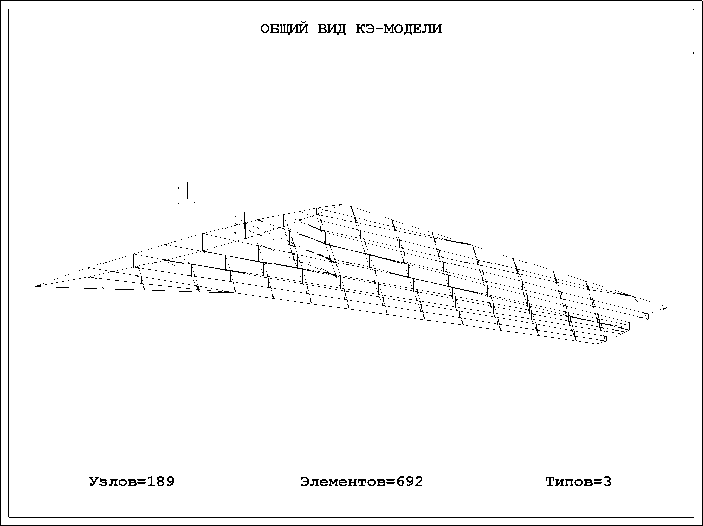
Рис. 1. Общий вид КЭ модели ГО.

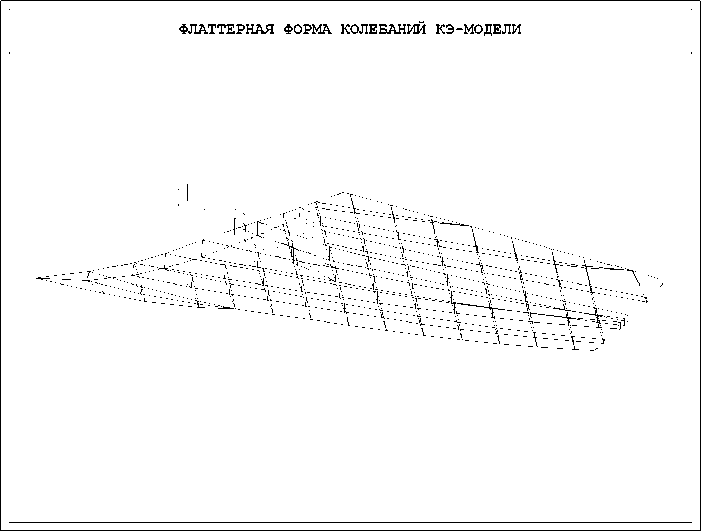
Рис. 3. Фаза A флаттерной формы КЭ модели.

рехугольные мембраны – для панелей нижней и верхней обшивок, стенок лонжеронов и нервюр; стержни – для верхних и нижних поясов лонжеронов и нервюр. Ось ГО моделировалась кессоном квадратного сечения со стороной, равной диаметру оси, который включал две группы панелей: верх-ние/нижние и передние/задние, а также группу из четырех стержней, идущих вдоль ребер кессона. Путем управления параметрами элементов этих трех групп было обеспечено равенство частот первых трех тонов колебаний КЭ модели ГО экспериментально измеренным значениям. Параметры остальных элементов ГО устанавливались в соответствии с технической документацией (чертежами). КЭ модель ГО имела 567 степеней свободы.

Фиксация КЭ модели ГО была осуществлена в двух поперечных сечениях кессона-оси, соответствующих двум бортовым узлам (подшипникам) вращения оси ГО. Упругость сервопривода учитывалась путем воспроизведения частоты крутильных колебаний ГО.

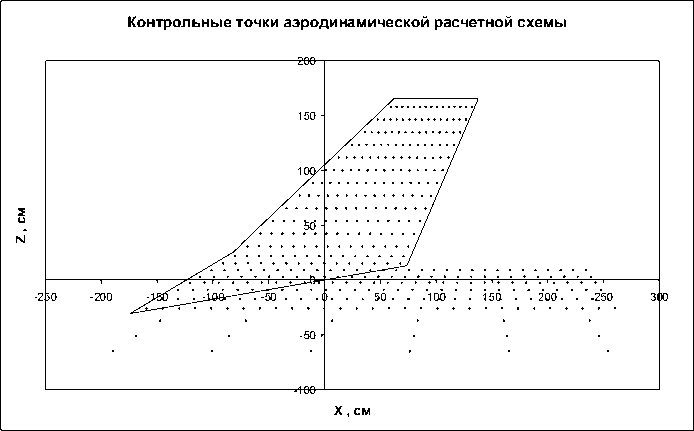
Рис. 2. Распределение контрольных точек по поверхности ГО и прилегающей части фюзеляжа.

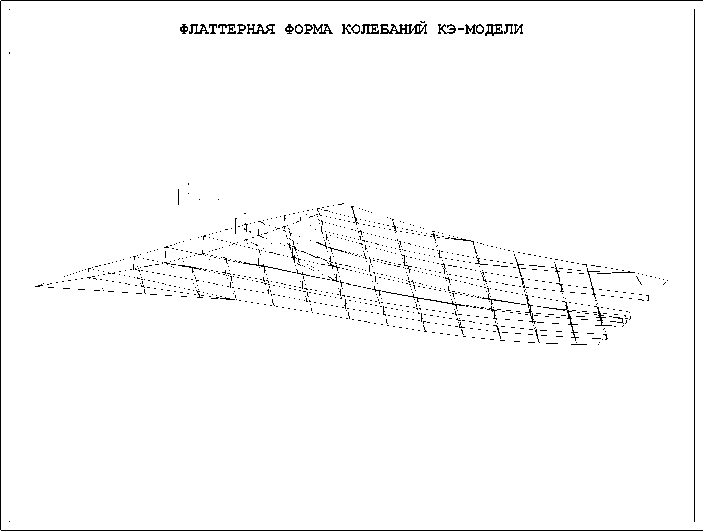
Рис. 4. Фаза B флаттерной формы КЭ модели.

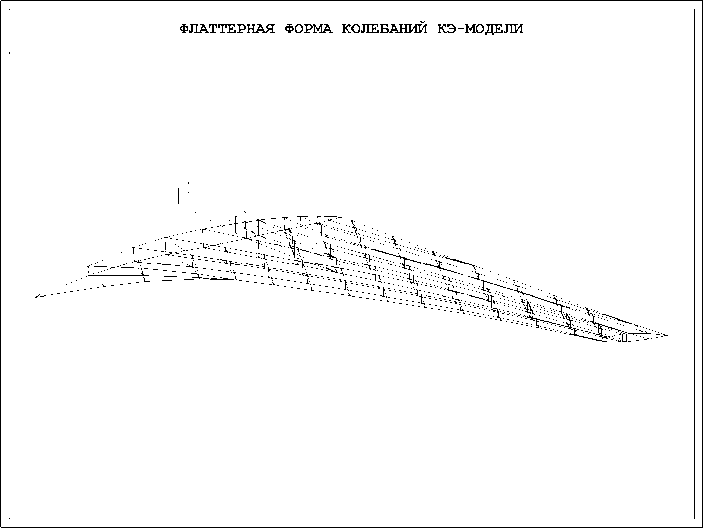
Рис. 5. Фаза C флаттерной формы КЭ модели.

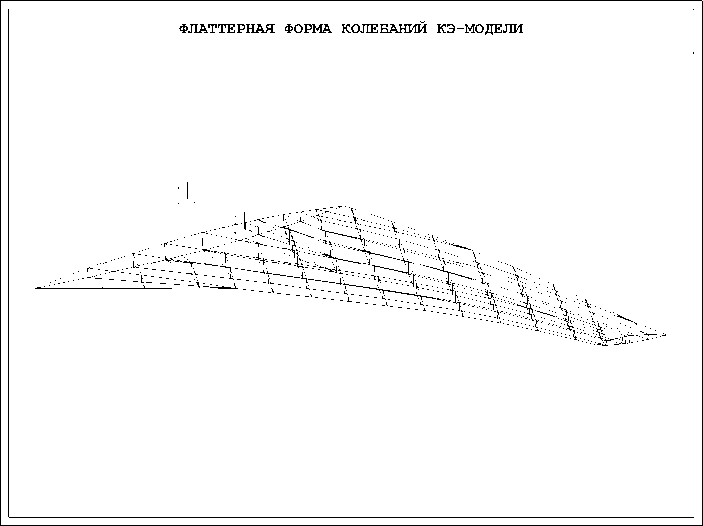
Рис. 6. Фаза D флаттерной формы КЭ модели.

Материал КЭ модели ГО (за исключением оси) соответствовал натуре.

Массовая модель ГО учитывала как силовую, так и несиловую части его массы. В силовую часть массы входила масса элементов КЭ модели ГО, в несиловую – технологическая масса конструкции ГО. Несиловая часть массы была включена в КЭ модель ГО в виде узловых масс. Массовая модель ГО соответствовала результату взвешивания ГО.

Аэродинамическая модель ГО построена на базе панельного метода [2,3]. Омываемая поверхность ГО и прилегающей части фюзеляжа были разбиты на поточные полосы, а полосы – на панели. В центре каждой панели выбрана контрольная точка. На рис. 2 изображены контрольные точки на поверхности ГО и на прилегающей части фюзеляжа (всего 408 точек). Матрица аэродинамического влияния вычислена для ряда заданных чисел Маха (0.85, 1.2, 1.5, 2.0, 2.5, 3.0). На рисунках 3–6 изображена флаттерная форма ГО в четырех после- довательных фазах с шагом π

Работы по исследованию частотных и флат-терных характеристик проектируемых конструкций ЛА на основе МКЭ [7,8] позволяют комплексно учесть аэроупругие характеристики ЛА на ранних этапах проектирования в процессе оптимизации конструктивно-силовой схемы и распределения силового материала и сосредоточенных масс и, тем самым, избежать ошибок, приводящих к последующим дорогостоящим работам по модификации и доводке конструкций.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009–2013 гг.