Решение задачи анализа звена мультисервисной сети связи

Современные мультисервисные сети связи (МСС) способны обрабатывать широкий спектр сообщений от традиционной телефонии до услуг с комплексным предоставлением информации (мультимедиа). При этом предо- ставляемые услуги требуют обеспечения различных требований к битовой скорости и, как следствие, организации каналов с различной пропускной способностью (табл. 1). Кроме того, данные услуги существенно отличаются по длительности обслуживания вызов пользователей. Так, телефонный разговор в среднем длится от 2 до 25 мин, тогда как продолжительность просмотра контента телевизионного вещания лежит в диапазоне от 10 мин до 3 часов.

Таблица 1. Требования различных услуг МСС к скорости передачи

Услуги		Технология кодирования	Скорость передачи
Речь	Телефония (очень высокого качества	МСЭ-Т, G.711	64 Кбит/с
	Телефония (высокое качество)	МСЭ-Т, G.729	8 Кбит/с
	Телефония (качество от высокого до удовлетворительного)	МСЭ-Т,G.723.1	5,3/6,4 кбит/с
Аудиоданные	Потоковое аудио	МР3	32 - 320 Кбит/с
	Музыкальный компакт диск	CD-DA	1441 Кбит/с
	Музыкальный компакт диск	MPEG с БПФ	192 – 256 Кбит/с
	Аудиозапись высокого качества	MPEG с БПФ	384 Кбит/с
Видеоданные	Видеоконференции	МСЭ-Т, Н.261	100 Кбит/с
	Потоковое видео	MPEG-4	до 10 Мбит/с
	Традиционное телевидение	MPEG-2	2 – 4 Мбит/с
	ЦТВ профессионального качества	МСЭ-Р ВТ.601	166 Мбит/с
	DVD-формат для DVD-дисков	MPEG-2	3 – 6 Мбит/с
	HDTV – телевидение высокой чёткости	MPEG-2	25 – 34 Мбит/с

Несмотря на большую размерность исходных данных для мультисер-висной модели системы распределения информации все основные результаты были получены по аналогии с ранее сформулированными для классической Эрланговской модели, которая нашла широкое применение в деятельности специалистов, занимающихся разработкой традиционных сетей связи с коммутацией каналов [1–3]. С учетом указанных факторов в мультисервис-ной модели исследуется процесс совместного использования общего канального ресурса звена МСС n пуассоновскими потоками вызовов (заявок), име- ющих различие в интенсивности поступления, объеме ресурса, который выделяется для обслуживания одной заявки, и времени его занятия. Данная мультисервисная система в теории телетрафика относится к новому классу многопотоковых моделей, в которых схема занятия канального ресурса зависит от типа поступившей заявки [2, 3]. При этом процессы обслуживания неординарных потоков заявок должны рассматриваются раздельно.

Рассмотрим мультисервисную систему обслуживания (рис. 1) на которую поступает n потоков заявок сервисов (услуг) реального времени (видеоконференцсвязь, речевые сообщения, аудиоконференцсвязь и др.). Заявки отличаются по ряду признаков и являются неординарными (маркированными).

Потоки заявок      Параметры       Передаточный репотоков            сурс линии в ЕКР

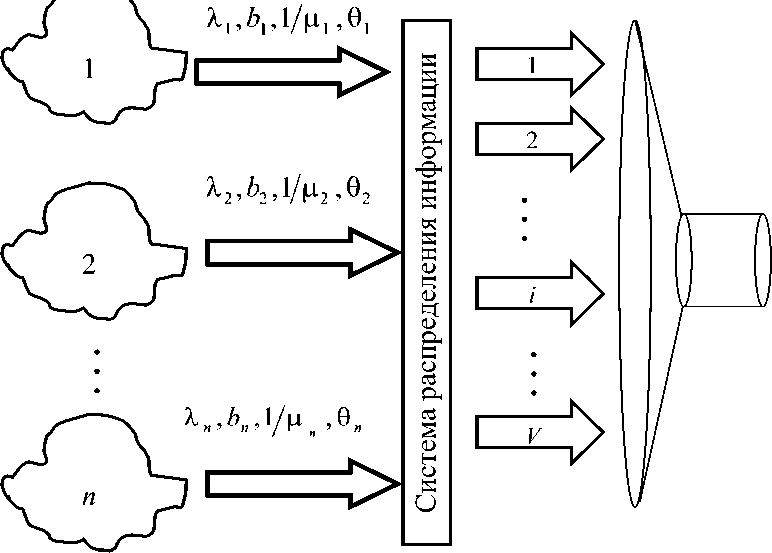
Рис. 1. Модель мультисервисной системы обслуживания с потерями.

Система полнодоступная однозвенная, способ обслуживания – с явными потерями. Скорость передачи информации в мультисервисной модели обозначается как V, является целым числом и выражается в единицах канального ресурса (ЕКР).

Количество источников нагрузки ( N k ), формирующих потоки нагрузки, не ограничено N k > 100. Поток заявок k -го потока ( k = 1, 2, .., n ) является Пуассоновским с интенсивностью поступления заявок 2 k .

Для того чтобы предоставить каждый из требуемых сервисов реального времени необходимо иметь b свободных единиц канального ресурса (ЕКР) звена МСС. Длительность занятия канального ресурса на обслуживание одной заявки к -го потока определяется как 1/ р^. Поток освобождений описывается экспоненциальным распределением с параметром р_к . Поступающая нагрузка от к -го потока в данном случае может быть вычислена по следующей формуле: ^Z _k =Х к /р к .

Стратегия доступа с резервированием каналов ( Trunk Reservation ) используется для доступа к передаточному ресурсу линии. Данная стратегия предусматривает введение индивидуального порога резервирования канального ресурса (РКР) для каждого к -го потока - 0_Л (0_t <  V ).

Пусть общее число занятых канальных единиц в момент поступления заявки равно i . При i >0 вновь поступившая заявка к -го потока теряется (получают отказ), повторно для обслуживания не поступает и в дальнейшем не оказывает влияние на систему. Во всех остальных случаях заявка принимается к обслуживанию.

Решение задачи анализа звена МСС сводится к определению вероятности потерь заявок ( п_к ) и доли обслуженной нагрузки ( Y k ) для каждого к -го сервиса ( к = 1,2,3,..., n. ) при заданных параметрах структуры ( V), входных потоках ( n , к_к , Ь_к , р^) и дисциплине обслуживания (0_t).

Анализ сети связи - это метод исследования существующей сети, характеризующийся выделением и изучением отдельных ее частей, а также характеристик и качества функционирования. Задачи анализа актуальны для существующих сетей связи. В классе задач анализа рассматриваются также вопросы расчета характеристик и параметров как сети в целом, так и отдельных ее элементов. К ним относятся задачи нахождения оптимальных путей передачи информационных сообщений, определения совокупности путей заданного транзитного пути, оценки пропускной способности канала, вероятности установления соединения между пунктами и т. д. Основная задача анализа сети состоит в расчете параметров сети в целом, параметров отдельных ее фрагментов и параметров ее элементов; аналогичные задачи возникают при учете возможности аварийного исключения узлов и линий для оценки живучести сети или без учета аварийных ситуаций для оценки надежности сети. Решение задачи синтеза звена МСС является обратной анализу и сводится к нахождению необходимого объема канального ресурса (V) при заданных значениях параметров потоков (n, kk, bk, р^), дисциплине обслуживания (3k) и нормах на потери заявок (пк < п*).

Для решения поставленной задачи анализа разработан алгоритм. В разработанном алгоритме метод Кауфмана–Робертса применяется для снижения вычислительной сложности [2]. Данный метод основан на разбиении пространства различных состояний модели по числу занятых ЕКР, позволяет эффективно вычислять нормированные вероятности величины обслуживания сервисов. Алгоритмы, построенные на основе данного метода, относят к классу "рекурсивных" с полиномиальной вычислительной сложностью [3].

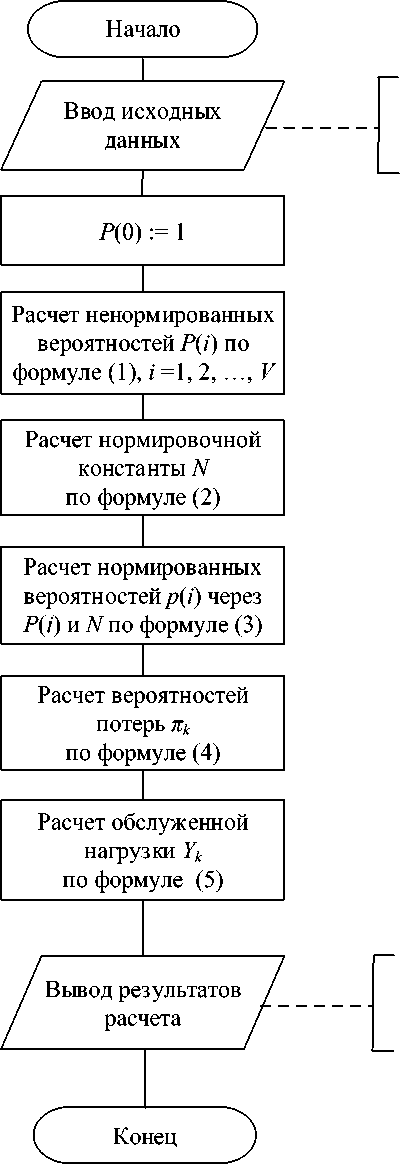
n, b k , X k , Ц k , V , © k , n *

π k , Y k

Рис. 2. Схема алгоритма анализа звена МСС

Под рекурсией здесь понимается процедура определения вероятностей потерь через предыдущие состояния системы. При решении задачи анализа МСС она сводится к выполнению последовательности следующих основных шагов (рис. 2):

Шаг 1. Ввести исходные данные:

• –    n – число услуг различных категорий (речь, данные, ВКС и др.);

• –    Z k – интенсивность нагрузки, поступающей от k- категории пользователей ( k = 1,2,..., n );

• –    b_k – ресурс канала, необходимый для обслуживания одной заявки k -го потока (категории);

• –    V – скорость выраженная в ЕКР, необходимая для передачи информации по мультисервисной линии.

• -    0 - индивидуальный порог резервирования канального ресурса

( 0 к <  V ).

Шаг 2. Приравнять значение нормированного параметра P (0) системы в нулевом состоянии к "1":

P (0) = 1.

Шаг 3. Последовательно увеличивая i в заданных пределах от 1 до V

( i = 1, 2,..., V ) вычислить из P (0) значения ненормированных вероятностей P ( i) по следующему соотношению:

n

P ( i ) = : - Z Z k ■ b k ■ P ( i - b k ) ■ ( 1 - 9 k ( i — b k ) ) ■ I ( i — b k ^ 0 ),       (1)

I   k = 1

где: I ( ■ ) - индикаторная функция, определяемая соотношением

I ( ■ ) =

[ 1,

I ^0,

если выполнено условие, сформулированное в скобках; если это условие не выполнено;

9 ( i ) - функция внутренней блокировки можно вычислить по формуле:

9 k ⁽ i ) = 9 k ^{( i}1 ^, i 2 ^,■■■^,i n )

0, если i = i 1 - b 1 + ... + i_n • b_n < 0 _k ;

1, в остальных случаях.

Шаг 4. Далее рассчитать значение нормировочной константы

V

N = Z P ( i ).

i = 0

Шаг 5. Определить нормированные значения вероятностей p ( i ) через ненормированные P ( i ) (шаг 5)

p ⁽ i ) =

P ( i )

• N

Шаг 6. Вычислить вероятность потерь вызовов потоков нагрузки реального времени для каждого k -го потока

V n k =S p(i) -ф k(i) .                               (4)

i = 0

Шаг 7. Рассчитать интенсивность обслуженной нагрузки реального времени для каждого k -го потока

Y _k = Z k • b_k - (1 -n _k )•                             (5)

Шаг 8. Вывести результаты расчета: π , Y .

Если полученные значения показателей качества обслуживания не удовлетворяют требуемым значениям ( π > π^∗ ), задача анализа может быть решена повторно при допустимом увеличении объема канального ресурса ( V ) звена МСС.

Таким образом, доведенные до программной реализации конструкции алгоритма являются универсальными и тем самым позволяют решать широкий перечень задач при исследовании МСС. При определенных исходных данных, правильном выборе нагрузочных и структурных параметров может быть исследован процесс обслуживания заявок, использующих различные стратегии доступа к канальному ресурсу звена МСС. Так, например при Vk = const - с кластеризацией (V1 + V2 +... + Vn = V). Кроме того, используя вместо формул (1) и (4), (5) выражения, полученные в [4], получаем возможность учесть приоритетную дисциплину обслуживания. Приняв bk = 1, расчет сводится к первой формуле Эрланга, которая традиционно используется для моносервисных сетей. А многократная реализация шагов предложенного алгоритма анализа при заданном качестве обслуживания и варьировании величины V в допустимой области значений обеспечивает решение задачи синтеза звена МСС.

При моделировании с различными исходными данными и сопоставлении полученных результатов с реальными значениями функционирования звена МСС, установлено, что данный подход позволяет получить приемлемые для практики результаты. Пример анализа звена МСС с использованием алгоритма и его программной реализации представлен в таблице 2. При заданных величине объема канального ресурса V и числе услуг n произвели расчет вероятности потерь π и объем обслуженной нагрузки Y .

В отличии от традиционных сетей связи, в который как правило заявки однородные, в звене МСС с неординарными заявками интуитивно предсказать поведение зависимостей показателей качества обслуживания от канального ресурса не представляется возможным. Как видно, даже при малой размерности исходных данных процедура расчета звена МСС является достаточно трудоемкой. При данных условиях прослеживается нелинейная зависимость зависимостей вероятностей потерь заявок для каждого типа трафика от канального ресурса звена МСС. В условиях гетерогенного трафика введение индивидуальных порогов резервирования является эффективным механизмом выравнивания потерь и реализации приоритетного доступа к общему канальному ресурсу мультисервисного звена для обеспечения требуемого качества обслуживания разнородных разноскоростных потоков заявок пользователей на уровне управления МСС.

Проведенные результаты исследований показал нелинейный характер зависимости вероятности потерь заявок от доступного объема канального ресурса в звене МСС. При увеличении количества потока заявок данный эффект усиливается. Без наличия соответствующих программного и технического обеспечения проблематично найти правильное решение по обеспечению заданного качества обслуживания мультисервисного трафика и выбору оптимальной стратегии (схему) доступа. Это подтверждает актуальность задач анализа мультисервисных сетей связи. Разработанное программное обеспечение позволяет с требуемой точностью быстро провести расчет звена МСС в широком диапазоне исходных данных, что свидетельствует о ценно- 10

сти разработанных модельно-алгоритмических конструкций для решения широкого перечня научно-практических задач. Следовательно, предложенное программное обеспечение может применяться в системе поддержки принятия решений должностных лиц и специалистов, занимающихся вопросами проектирования и эксплуатации МСС.

"Экономика и социум" №5(84) 2021