Научные статьи \ Математика. Естественные науки \ Математика \ Математическая кибернетика

Решение задачи бинарной классификации с помощью методов машинного обучения

Автор: Даньшина А.А., Бабенко А.А.

Журнал: НБИ технологии @nbi-technologies

Рубрика: Информационные технологии в безопасности и телекоммуникациях

Статья в выпуске: 3 т.18, 2024 года.

Бесплатный доступ

В данном исследовании рассмотрены модели машинного обучения для решения задачи бинарной классификации. Представлен алгоритм обработки набора данных для обучения и тестирования, а также проведен сравнительный анализ предлагаемых моделей, по итогу которого была определена наиболее рациональная модель машинного обучения для выполнения поставленной цели.

Бинарная классификация, модели машинного обучения, набор данных, распределение данных, корреляци

Короткий адрес: https://sciup.org/149147330

IDR: 149147330 | УДК: 519.7 | DOI: 10.15688/NBIT.jvolsu.2024.3.4

Текст научной статьи Решение задачи бинарной классификации с помощью методов машинного обучения

DOI:

В нынешнее время количество различных алгоритмов машинного обучения позволяет сделать выбор в пользу данного средства для решения разноплановых задач. Преимущество этих технологий обуславливается тремя важными факторами для большинства

компаний, разрабатывающих системы информационной защиты: низкая стоимость, простота реализации, скорость обучения и предоставления результата.

Для обучения любой системы необходимо сформировать структурированный и обрабо- танный массив данных – датасет. Классической задачей фильтрации и классификации набора информации является дихотомическая или же бинарная классификация. Определение принадлежности объекта к одному из двух возможных классов – основная цель рассматриваемой задачи [3]. Ее решение находят с помощью различных моделей машинного обучения. Для определения наиболее рациональной из них, сформируем датасет, на основе которого, в последствии, будет происходить обучение (рис. 1) [1].

Необходимо убедиться, что в сформированных столбцах нет пропущенных значений. Данный пул имеет 86 непустых записей по 7 критериям, описания которых представлены в таблице.

Так как в датасете присутствуют три категориальных поля, таких как location, merchant и gender, необходимо перевести их уникальные значения в числовые, используя метод One-hot encoding.

Таким образом получим перечень из следующих преобразований:

a) gender: M -1, F- 0;
b) location: New York – 1, Chicago – 2, Los Angeles – 3, San Francisco – 4;

c)merchant: ABC Corp – 0, XYZ Inc – 1.

Основываясь на преобразованных данных (рис. 2), произведем оценку корреляции между столбцами числовых признаков. Полученная матрица корреляция отображается в

	transaction_id	transaction_amount	location	merchant	age	gender	fraud_label
0	1	1000.0	New York	ABC Corp	35	M	0
1	2	500.0	Chicago	XYZ Inc	45	F	0
2	3	2000.0	Los Angeles	ABC Corp	28	M	1
3	4	1500.0	San Francisco	XYZ Inc	30	F	0
4	5	800.0	Chicago	ABC Corp	50	F	0
81	82	1500.0	Los Angeles	XYZ Inc	31	M	0
82	83	2800.0	San Francisco	ABC Corp	50	F	1
83	84	1350.0	Chicago	XYZ Inc	28	M	0
84	85	920.0	New York	ABC Corp	47	F	0
85	86	2000.0	Los Angeles	XYZ Inc	36	M	0

86 rows * 7 columns

Рис. 1. Сформированный массив данных

Описание критериев данных

Название критерия	Описание	Тип данных	Описание типа данных
transaction_id	Номер транзакции	Int64	Целочисленный 64х-битный
transaction_amount	Сумма транзакции	Float64	Нецелочисленный 64х-битный
location	Место выполнения транзакции	object	Набор свойств
merchant	Платёжная система	object	Набор свойств
age	Возраст	Int64	Целочисленный 64х-битный
gender	Половая принадлежность	object	Набор свойств
fraud_label	Метка мошенничества	Int64	Целочисленный 64х-битный

transaction_id	transaction_amount	location	merchant	age	gender	fraud_label
0 1	1000.0	1	0	35	1	0
1 2	500.0	2	1	45	0	0
2 3	2000.0	3	0	28	1	1
3 4	1500.0	4	1	30	0	0
4 5	800.0	2	0	50	0	0
81 82	1500.0	3	1	31	1	0
82 83	2800.0	4	0	50	0	1
83 84	1350.0	2	1	28	1	0
84 85	920.0	1	0	47	0	0
85 86 86 rows ^x 7 columns	2000.0	3	1	36	1	0

Рис. 2. Данные в числовом формате том случае, если значение ее модуля превышает отметку 0,3 (рис. 3).

После предобработки данных датасета и определения корреляционной матрицы, можем отобразить графики распределения данных (рис. 4).

Для дальнейшего определения наилучшей модели машинного обучения, необходимо разбить данные на две группы: тестовые и обучающие. Так как в нашем датасете число записей меньше 1000, то соотношение будет 70:30, где 70 – процентное количество данных для обучения, а 30 – для тестирования [4].

Для сравнительного анализа выберем следующие модели машинного обучения: логическая регрессия, метод опорных векторов, дерево решений, наивный байесовский классификатор, метод k -ближайших соседей, XGBoost, градиентный бустинг, метод случайного леса, AdaBoost. Метрикой оценки качества моделей будет выступать F1-Score – гармоническое среднее между точностью и пол-

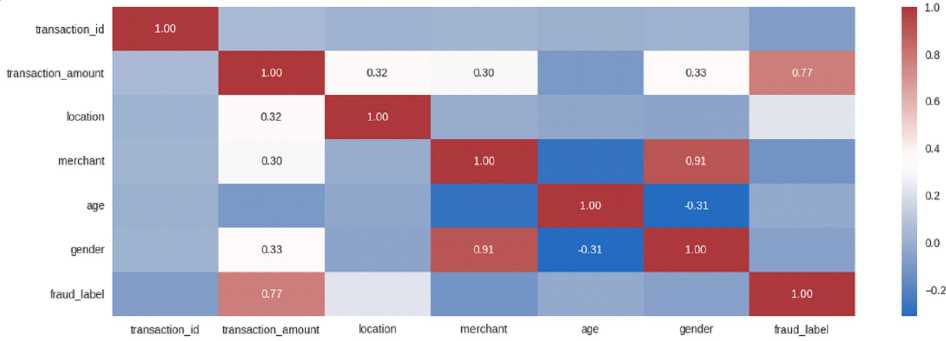
Рис. 3. Матрица корреляции столбцов числового признака

Рис. 4. Графики распределение данных

нотой [4]. Для каждой модели гиперпараметры были определены по умолчанию (рис. 5).

Сравнительный анализ показал, что наилучшей моделью машинного обучения для решения задачи бинарной классификации по метрике F1-Score и настроенных гиперпараметрах по умолчанию является AdaBoost.

Ключевой проблемой данной модели является склонность к переобучению при наличии значительного уровня шума данных [2]. Одним из методов решения является определение наиболее влиятельных гиперпараметров для предсказания алгоритма. Такими являются: максимальная глубина дерева решений {1,2,3,4,5,6} и количество деревьев в ансамбле {1,2,3…2500} [5].

Все рассмотренные модели машинного обучения справляются с поставленной целью – решение задачи бинарной классификации. Однако наиболее рациональной в использовании оказалась модель AdaBoost, применяющаяся в связке со слабым алгоритмом одноуровневых деревьев решений. Высокая эффективность достигается за счет бустинга слабых классификаторов, что также компенсирует такую проблему модели, как переобучение.

Дальнейшим вектором научных исследований является рассмотрение эффективности алгоритма AdaBoost при решении других задач классификации.

Список литературы Решение задачи бинарной классификации с помощью методов машинного обучения

%94 Accuracy All Classifiers Fraud Detection // Kaggle. - Electronic text data. - Mode of access: https://www.kaggle.com/code/tayfundogruer/94-accuracy-all-classifiers-fraud-detection.
Алгоритм AdaBoost // Хабр. - Электрон. текстовые дан. - Режим доступа: https://habr.com/ru/companies/otus/articles/503888.
Как заставить работать бинарный классификатор чуточку лучше // Хабр. - Электрон. текстовые дан. - Режим доступа: https://habr.com/ru/articles/228963.
Метрики оценки качества моделей и анализ ошибок в машинном обучении. Подробное руководство // Хабр. - Электрон. текстовые дан. - Режим доступа: https://habr.com/ru/articles/821547.
Повороты признаков в алгоритме AdaBoost // OSP. - Электрон. текстовые дан. - Режим доступа: https://www.osp.ru/netcat_files/userfiles/Hadoop_TBD_2_2016/Goy_tbd_2.pdf.