Решение задачи Дородницына
Автор: Сизых Г.Б.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Механика
Статья в выпуске: 4 (56) т.14, 2022 года.
Бесплатный доступ
Решается задача строгого обоснования факта максимальности энтропии на гладкой выпуклой носовой части поверхности тела, обтекаемого однородным сверхзвуковым потоком идеального газа в несимметричном случае. М. Д. Ладыженским еще до 1968 года было предложено доказательство этого факта, но только для тел вращения при некоторых малых углах атаки. Какая-либо оценка диапазона таких углов отсутствовала. В связи с этим академик А. А. Дородницын в 1968 году констатировал отсутствие строгого обоснования максимальности энтропии на гладкой выпуклой носовой части поверхности тела даже для тел вращения (тем самым поставив задачу найти такое обоснование). Для несимметричных носовых частей и для осесимметричных тел под углом атаки строгое обоснование было получено Г. Б. Сизых в 2019 году. Соответствующее доказательство было опубликовано в кратком виде так, что обоснованность некоторых шагов доказательства оказалась сложна для понимания. Доказательство 2019 года приводится в развернутом виде, с подробным обоснованием всех шагов.
Уравнения эйлера, изоэнтальпийные течения, завихренность, линия торможения, лидирующая линия тока, отошедший скачок уплотнения
Короткий адрес: https://sciup.org/142236630
IDR: 142236630 | УДК: 533.6.011
Текст научной статьи Решение задачи Дородницына
В сборнике статей [1], посвященном гиперзвуковым течениям газа, помещено сообщение, в котором академик А. А. Дородницын пишет: «При нулевом угле атаки на. поверхности тела. вращения энтропия принимает максимальное значение. Многие расчеты и эксперименты показывают, что и при углах атаки, отличных от нуля, с точностью, которая получена, в этих расчетах или эксперименте, энтропия сохраняет свое максимальное значение. Однако
«Московский физико-технический институт (национальный исследовательский университет)», 2022
никакого строгого доказательства этого факта нет». Затем А. А. Дородницын приводит одно доказательство, которое в разговоре ему сообщил М. Д. Ладыженский. Выкладки М. Д. Ладыженского приводят к выводу о существовании некоторого ненулевого диапазона углов атаки, при которых энтропия на поверхности тела вращения будет оставаться максимальной. Отсутствие не только точного значения, но и каких-либо оценок упомянутого диапазона углов атаки, означало, что вопрос решен лишь частично и только для тел вращения.
В данной статье рассматриваются произвольные углы атаки и тела, которые могут быть не только телами вращения. Задачу строгого обоснования факта максимальности энтропии на гладкой выпуклой носовой части поверхности тела здесь предложено назвать задачей Дородницына.
При сверхзвуковом (число Маха М > 1) обтекании тел с гладкой выпуклой носовой частью возникает отошедший головной скачок. Если осесимметричное тело расположено так, что ось симметрии параллельна скорости набегающего потока (нулевой угол атаки), то линия торможения АВ, лежащая на этой оси, заканчивается на теле в точке торможения В (которую также называют передней критической точкой). При этом точка А расположена на скачке там, где касательная к скачку плоскость перпендикулярна скорости набегающего потока (такая точка называется лидирующей точкой скачка, а проходящая через нее линия тока - лидирующей линией тока, или, для краткости, лидирующей линией). Поэтому параметры течения в точке В можно рассчитывать по параметрам набегающего потока. Для этого достаточно использовать условия Ренкина - Гюгонио на прямом скачке [2] в точке А и условие сохранения энтропии на линии торможения. Очевидно, что в этом случае энтропия принимает максимальное значение на линии торможения и на поверхности тела.
Если же есть угол атаки или тело не осесимметрично, то максимальное значение энтропии будет на лидирующей линии тока (на линии тока, пересекающей скачок по нормали). Поэтому обоснование максимальности энтропии сводится к доказательству совпадения линии торможения с лидирующей линией.
2. Обозначения и уравнения движения
Рассмотрим стационарное обтекание тела с гладкой выпуклой носовой частью однородным сверхзвуковым потоком идеального совершенного газа без предположения о какой-либо симметрии. Поскольку носовая часть гладкая и выпуклая, отошедший головной скачок уплотнения также будет иметь гладкую выпуклую форму. При этом ниже по течению могут находиться другие скачки уплотнения и тангенциальные разрывы.
Будем считать, что в течении существует ограниченная область G, замыкание G которой расположено между головным скачком и носовой частью, обладающая следующими свойствами. Линия торможения АВ, за исключением точки А ее начала на скачке и точки торможения В на теле, лежит внутри замкнутой области G (рис. 1). При этом часть границы G, лежащая на поверхности тела, представляет собой замыкание двухмерной окрестности точки В, а часть границы, лежащая на скачке, представляет собой замыкание двухмерной окрестности точки А. Оставшаяся же часть границы вместе с внутренними точками G находится внутри зоны течения, в которой отсутствуют скачки и разрывы, и отсутствуют другие точки торможения (кроме точки В).
Пусть прямоугольная декартова система координат Вжуz с началом в точке В сориентирована так, что ось z нормальна к поверхности тела в точке В и направлена внутрь тела. Будем считать, что поверхность тела в некоторой окрестности точки В представляется в виде Н2 = {ж, y,z : z = у(ж,у), (ж, у) G S }, г де у(ж,у) - функция, дважды непрерывно дифференцируемая на замыкании S некоторой ограниченной области S перемсшіых (ж, у). II при этом существует такое число Az > 0. что область (слой) Нз = {ж,у,z : у(ж,у) < z < у(ж,у) + Az, (ж, у) G S } лежит внутри тела. (Нижние индексы 2 и 3 подчеркивают, что Н - поверхность, а Н3 - трехмерная область.)
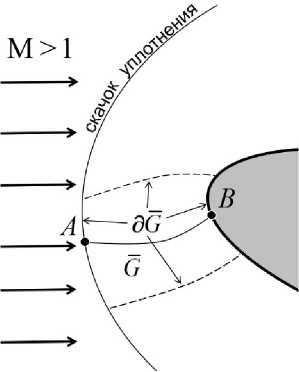
Рис. 1. Замкнутая область G и ее граница dG. Линия торможения, за исключением точек Ам В, лежит внутри G
Точка торможения В является точкой растекания, и в ней начинаются линии тока, растекающиеся во всех направлениях по поверхности тела. При этом, по крайней мере, в некоторой окрестности точки В только линия торможения имеет точки внутри течения и одну точку на поверхности тела (точку В). Остальные линии тока в этой окрестности, как схематично показано на рис. 2, либо не контактируют с поверхностью тела (линии тока, проходящие над поверхностью), либо целиком лежат на поверхности тела (линии тока, начинающиеся в точке В).
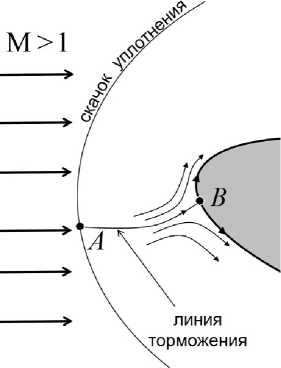
Рис. 2
Дальнейшее исследование будет существенным образом опираться на сформулированное выше предположение о единственности линии торможения (которая имеет точки внутри течения и только одну точку на поверхности тела). Это предположение общепринято. Для различных типов жидкости оно подтверждается расчетами (например, [3-6]) и известными точными решениями (например, безвихревое обтекание сферы несжимаемой жидкостью), а в учебниках и в теоретических исследованиях [1, 7-11] это предположение даже не обсуждается, и при описании картины обтекания используется как нечто само собой разумеющееся (при гладком стационарном обтекании гладкого выпуклого тела). Также предположение о единственности линии торможения для выпуклых носовых частей подтверждается и экспериментальными данными [12]. Однако это предположение исключает из рассмотрения плоские (точнее сказать, плоскопараллельные) течения, поскольку в таких течениях поверхность торможения состоит из бесконечного числа линий торможения.
В рамках настоящей работы не удалось решить вопрос о начале линии торможения в плоском случае, и дальнейшее исследование проводится только для трехмерного течения, не вырожденного в плоскопараллельное.
Обозначим: V - вектор скорости, р - плотность, р - дав.теине. Q = rotV - вектор завихренности. Давление р и плотность р в замкнутой области G связаны соотношением рр-к = а, где к - показатель адиабаты, а - энтропийная функция, которая может быть различной на различных линиях тока.
Поскольку точки замкнутой области G, за исключением граничных точек на скачке и на теле, являются внутренними точками зоны течения, в которой отсутствуют скачки и разрывы, то будем считать, что в этих точках параметры течения (компоненты скорости, р и р) являются дважды непрерывно дифференцируемыми функциями пространственных координат. Кроме того, поскольку поверхности скачка и тела являются гладкими, будем считать, что параметры течения и их первые и вторые производные допускают непрерывное продолжение из внутренних точек замкнутой области G как на поверхность скачка, так и на поверхность тела. Под значениями производных на упомянутых поверхностях будем понимать их непрерывные продолжения из внутренних точек G. (Таким образом, предполагается непрерывность первых и вторых производных во всех точках замкнутой области G.)
Замечание. Предположение о непрерывности первых и вторых производных во всех точках G не противоречит тому, что кривизна линий тока не ограничена в окрестности точки торможения, и поле единичного вектора, касательного к линиям тока, имеет разрыв в точке торможения. Подобная картина имеет место, например, в точных решениях уравнений для задач обтекания сферы и цилиндра идеальной несжимаемой жидкостью [7] или в точном решении, приведенном Бэтчелором в [13, параграф 2.7]. В этих точных решениях компоненты скорости и их первые и вторые производные ограничены и допускают непрерывное продолжение на поверхность тела в окрестности точки торможения, но при этом максимальная кривизна линий тока неограниченно возрастает по мере их приближения к точке торможения, и поле единичного вектора, касательного к линиям тока, имеет разрыв в точке торможения. Также следует учесть, что точные решения с разрывами вторых производных параметров течения в окрестности точки торможения неизвестны.
Течение газа в замкнутой области G подчиняется уравнению неразрывности div(p V ) = 0. Набегающий поток однороден. Поскольку полная энтальпия io = (к/(к — 1))(р/р) + V 2/2 не меняется при пороходе через скачок, поле io однородно во всех точках течения ( Vio = 0). В этом случае стационарные уравнения Эйлера в форме Крокко [13, 14] записываются следующим образом:
Q х V = (к — 1)-1рp-1Vlna. (1)
3. Следствие из критерия Зоравского
Критерий Зоравского [15, 16], который также называется теоремой Фридмана [17, 18], обобщает теоремы Гельмгольца о вихрях и в некоторых случаях позволяет исследовать векторные линии других векторов (а не только вектора завихренности). В этом случае частицы, составляющие векторные линии, движутся со скоростью, вообще говоря, не совпадающей со скоростью жидкости. Поэтому обычно [19-21] при использовании критерия Зоравского вводится понятие воображаемой жидкости, состоящей из таких частиц.
Сформулируем следствие из критерия Зоравского [15, 16] для частного случая стационарного и соленоидального векторного поля с (в области G).
Следствие из критерия Зоравского. Если в области G стационарное векторное поле q непрерывно дифференцируемо, а стационарное и соленоидальное поле с (div c = 0) дваэюды непрерывно дифференцируемо и выполняется равенство
то воображаемые частицы, составляющие в некоторый момент времени открытый сегмент (то есть не включающий свои крайние точки) векторной линии с, лежащий в области G, двигаясь со скоростью q, будут составлять открытый сегмент одной из векторных линий с в каждый последующий момент времени (до тех пор, пока эти частицы находятся в области G). Такие воображаемые частицы будем называть (/-частицами. В данном разделе в качестве вектора с будет рассмотрен соленоидальный вектор pV.
Используем следствие из критерия Зоравского и понятие воображаемой жидкости для исследования векторных линий вектора pV, совпадающих с линиями тока газа. Для этого в замкнутой области G наряду с течением (реального) газа рассмотрим течение воображаемой жидкости, частицы которой ((/-частицы) движутся со скоростью q = а^/р, где коэффициент а = 1кг/с2 обеспечивает для q размерность скорости ([ q ] = м/с). Эти (/-частицы не взаимодействуют с газом и не влияют на течение газа.
Уравнение (1) может быть записано в виде (p V ) х q = — а(к — 1)-1 V ln а. Поэтому rot ((p V ) х q ) = 0, из чего следует равенство (2) для с = pV . Согласно следствию из критерия Зоравского, равенство (2) есть достаточное условие для того, чтобы /-частицы, составляющие открытый сегмент линии тока газа (то есть открытый сегмент векторной линии pVV лежащий в области G в некоторый момент времешв двигаясь со скоростью q. составляли открытый сегмент одной из линий тока газа в каждый последующий момент времени (до тех пор, пока эти /-частицы находятся в области G).
4. Теоремы об автономных системах обыкновенных дифференциальных уравнений
Движение /-частиц рассматривается не только в области G, где выполняется следствие из критерия Зоравского, но и на границе этой области, то есть во всей замкнутой области G. Поэтому с использованием этого следствия будем рассматривать движение /-частиц только в области G, а движение во всей замкнутой области G будем рассматривать с использованием известных теорем об автономных системах обыкновенных дифференциальных уравнений (в дальнейшем - ОДУ). Положение /-частицы в течение отрезка времени [to,t1] определяется как решение автономной еіістсмы ОДУ. правая часть которой равна q. а начальным условием является положение /-частицы в момент времени to (автономность системы следует из стационарности поля q). Широко известные теоремы об автономных системах ОДУ [22-26] доказаны для (открытых) областей. Ниже с использованием этих теорем будет рассмотрено движение /-частиц, лежащих в момент времени to на полуоткрытом сегменте линии торможения, включающем точку торможения В (лежащую на границе). При этом будут использованы два утверждения из теории автономных систем ОДУ. Первое - о непрерывной зависимости от начальных условий. Из этого последует непрерывность в течение некоторого отрезка времени [to, ti] линии, состоящей из частиц, лежащих в момент времени to на упомянутом выше полуоткрытом сегменте линии торможения. Второе - следствие теоремы существования и единственности о том, что в области, где q не обращается в нуль, траектории /-частиц не пересекаются (не имеют общих точек). Покажем, что эти утверждения верны для /-частиц, расположенных в пересечении некоторой окрестности точки В с замкнутой областью G.
Сначала заметим, что в условиях теорем [22-24], из которых следуют два упомянутых утверждения, к полю q предъявляется требование гладкости. Однако в доказательствах используется только следствие гладкости - условие Липшица. А, например, в [25, 26] условие Липшица вводится в условия соответствующих теорем сразу (без требования гладкости). Воспользуемся возможностью ограничиться условием Липшица (вместо гладкости).
Используем обозначения третьего абзаца второго раздела, где были введены в рассмотрение поверхность Н2 = {ж, у, г : г = р(ж,у), (ж,у) G S} и область (слой) Нз = {ж, у, г : р(ж,у) < г < р(ж,у) + Аг, (ж, у) G S}. Без ограничения общности можно считать, что область S настолько мала, что поверхность Н2 находится внутри части границы G, лежащей на поверхности тела. Поэтому на Н2 определен век- тор q(x, у, z) и на новерхности Н его можно представить зависящим от двух переменных: q(x,y, z) = q(x, у, р(х, у)), (х,у) Е S . Опре делим q в слое Н3 по формуле q(x,y,z) = q(x, у, ^(х, у)) (в этом слое q но завіісит от zV Тогда поле q окажется непрерывным и кусочно-гладким (возможен разрыв производных компонент q на поверхности тела) в области У, состоящей из внутренних точек объединения G UH3. Однако, поскольку функция ^(х,у) дважды непрерывно дифференцируема. на. замыкашш S. производные компонент q будут ограничены, и условие Липшица в области У будет выполнено. Таким образом, часть границы G, лежащей на теле (а именно Н2), окажется погруженной в область У, для которой справедливы теоремы [22-26] о существовании и единственности решения и о непрерывной зависимости решения от начальных условий. Из чего следует непрерывность линии (по крайней мере, в течение некоторого отрезка времени [to, ti]), состоящей из q-частиц, лежащих в момент времени to на полуоткрытом сегменте линии торможения, включающем точку торможения В.
Теперь, когда установлена возможность применять теоремы [22-26] к точкам, расположенным на поверхности Н2, уточним кар тину течения q-частиц вблизи этой поверхности (которая есть окрестность точки торможения В, лежащая на поверхности тела). Точка В есть точка растекания газа. Поэтому энтропийная функция на поверхности тела равна своему значению в точке В, и, следовательно, вектор Vһія ортогонален поверхности тела. Вместе с уравнением (1) это означает, что в тех точках поверхности тела, где V = 0, вектор q лежит в касательной к поверхности тела (к поверхности Н2) плоскости. По сделанному во втором абзаце подраздела «обозначения и уравнения движения» предположению V = 0 всюду, кроме точки В. То есть q лежит в касательной к поверхности Н плоскости всюду, кроме точки В. Из непрерывности q следует, что и в точке В век тор q также лежит в касательной к поверхности Н плоскости (нормальная к поверхности Н компонента q равна нулю).
Допустим, что в некоторой точке Е Е Н скор ость q равна нулю. Воображаемая q-частица, находящаяся в этой точке неподвижна. Теория автономных систем ОДУ допускает существование других q-частиц, приближающихся к точке Е, но такое приближение (если оно имеет место для точки Е) будет асимптотическим, и эти (другие) q-частицы не могут попасть в точку Е за конечное время. Действительно, если одна из таких частиц, бывшая в точке Е ‘ = Е в момент времени to, окажется в точке Е в (конечный) момент времени ti > to, то задача с начальным (в момент ti) значением координат, равным коор-дппатам точки Е. для автономной системы OД^'. правая часть которой равна, — q. будет иметь два. различных решения. Это противоречит теореме существования и единственности. Поэтому щнастнпы не могут выйти из G через точку Е Е Н2. ckoj: юсть q в которой равна, нулю.
Теперь допустим, что в некоторой точке Е Е Н скор ость q отлична от нуля. Тогда, в силу непрерывности, скорость q будет отлична от нуля в некоторой окрестности точки Е. Поскольку нормальная составляющая q к поверхности Н равна нулю, на поверхности Н будет лежать сегмент векторной линии q, для которого точка Е будет внутренней точкой. Такой сегмент есть часть фазовой траектории (для автономной системы ОДУ с правой частью, равной q). В силу теоремы существования и единственности внутренняя точка (точка Е) этой траектории не может принадлежать какой-либо другой фазовой траектории. Поскольку фазовые траектории рассматриваемой автономной системы ОДУ есть траектории д-чаетиц. приходим к выводу, что q-частипы также не могут выйти из G и через точку Е Е Н2, скор ость q в которой отлична от нуля.
Таким образом, q-частицы не могут покидать замкнутую область G через поверхность Н2. С учетом такого уточнения картины течения можно утверждать, во-первых, что в течение некоторого отрезка времени [to, ti] линия, состоягуая из q-частиу, лежащих в момент времени to на полуоткрытом сегменте линии торможения, содержащим точку В. будет оставаться непрерывной линией и находиться в замкнутой области G. Во-вторых, что если в некоторой окрестности точки В скоростъ q = 0, то в этой окрестности траектории q-частиц не пересекаются (не имеют общих точек). Кроме того, в случае q = 0, поскольку на поверх пости тела вектор q лежит в касательной к поверхности тела плоскости, траектории q-частиц, имеющие хотя бы одну точку на поверхности тела, целиком лежат на этой поверхности (в упомянутой окрестности). Ниже будем ссылаться на эти утверждения как на следствия теорем [22-26].
5. Завихренность в точке торможения
Докажем, что завихренность Q в точке торможения В равна нулю, то есть, что ^(B) = 0. Доказательство проведем методовi «от противного». Допустим, что ^(B) = 0. Тогда q(B) = 0.
Величина проекции скорости q в произвольной точке замкнутой области G на вектор q(B) = 0 равна, (q • q(B))/|q(B)|. г,те (q • q(B)) - скалярное проігзвелешіе векторов q ii q(B). В точке B эта величина равна |q(B)|. В силу нейрерывности q, существует такая (достаточно малая) шаровая окрестность G b точки B, что часть этой окрестности GB, занятая течением газа, лежит в G (GB = G b П G, рис. 3.), часть границы Gb, лежащая на теле, принадлежит Н2 и во всех точках G b проекция скорости q па вектор q(B) = 0 не меньше 0.5|q(B)| > 0. (Множество G b не является областью, т.к. ему принадлежит часть его границы, лежащая на теле.)
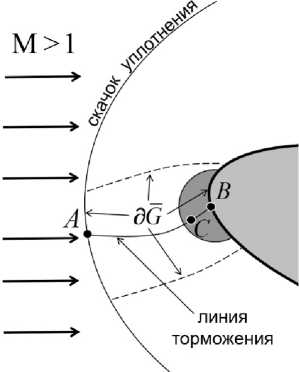
Рис. 3. Множество G b обозначено темно-серым цветом
Пусть С - точка на линии торможения AB' обозначим: (CB) - открытый сегмент линии торможения между точками C и B. Выберем точку С так, чтобы сегмент (CB ) целиком лежал в G b (рис. 3). Обозначим: Q(CB) - совокушюсть g-частиц. которые составляют открытый сегмент (CB) в момент времени to; Q(CB] - совокупность g-частиц, которые составляют полуоткрытый (включающий точку B) сегмент (CB] в момент времени to (в этот момент щнаетипы Q(CB ] составляют непрерывную кривую); Q(B) Е Q(CB\ - щнастипа. которая находится в точке B в момент времени to. Частицы Q(CB] движутся со скоростью q. Согласно первому следствию теорем [22-26] (см. выделенное курсивом в конце предыдущего раздела), эти g-частицы в течение некоторого времени будут составлять непрерывные кривые и находиться в Gb-
Все g-частицы, находящиеся в Gb, движутся с ненулевой скоростью, и их координата в направлении q(B) меняется со скоростью не менее 0.5|q(B)|. Согласно второму следствию теорем [22-26] (см. выделенное курсивом в конце предыдущего раздела), поскольку скорость q нс равна иу.тто. траектории щнастип. лежащие в Gb- ио пересекаются (не имеют общих точек). Кроме того, поскольку на поверхности тела вектор q = 0 лежит в касательной к поверхности тела плоскости, траектории g-частиц, имеющие хотя бы одну точку на поверхности тела, целиком лежат на этой поверхности (в Gb)- Поэтому из предположения
Q(B) = 0 вытекает, что в течение некоторого отрезка времени [to,ti] частица Q(B) будет двигаться по поверхности Н2, лежащей на теле, а остальные частицы Q(CB ) будут при движении оставаться во внутренних точках течения. Кроме того, поскольку проекция скорости q в G b на вектор q(B) = 0 не меньше 0.5|q(B)| > 0, для любого момента времени t Е (^о, ti] частица. Q(B ) будет находиться на поверхности тела в точке D = D(t) = В на поверхности Н2. Но, согласно критерию Зоравского, частицы Q(CB) в момент времени t Е (to , ti] должны составлять открытый сегмент одной из линий тока газа. Поскольку Q(CB) Е Q(CB ]. в силу непрерывности липни, составленной и:з частиц Q(CB] ото означает, что в сколь угодно малой окрестности точки B должна существовать линия тока газа, лежащая во внутренних точках течения, не совпадающая с линией торможения и примыкающая к поверхности тела в точке D = B на поверхности тела (рис. 4).
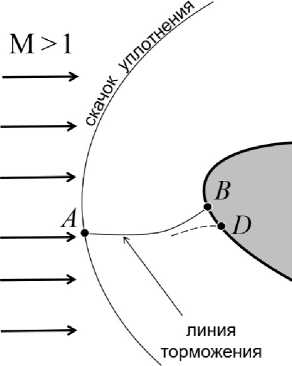
Рис. 4. Гипотетическая линия тока, (изображена, штрихами), существование которой вытекает из предположения о том, что завихренность в точке торможения отлична, от нуля
Но это противоречит картине течения, описанной выше в четвертом абзаце второго раздела. Поэтому предположение о том, что Q(B) = 0, неверно, то есть Q(B ) = 0. Этот факт есть один из основных результатов раздела и будет использован ниже.
6. Завихренность на линии торможения
Выше рассматривался сегмент (CB ] линии торможения, лежащий в Gb- Из-за ограни-чешюсти G b возможна ситуация, при которой начало этого сегмента (тонка C) не может быть выбрано как угодно близко к точке А на скачке. Теперь рассмотрим сегмент (CB], в котором точка C может находиться сколь угодно близко к точке А, но лежит внутри замкнутой области G, то есть C Е (AB ). Используем введенные выше обозначения для B и Q(B), (CB) и Q(CB ), (CB] и Q(CB], Согласно критерию Зоравского, щчастицы, составляющие (CB) в момент времени to (то есть частицы Q(CB )). двигаясь с о скоростью q. в каждый последующий момент (пока находятся в G) составляют открытый сегмент одной из линий тока. газа. Согласно первому следствию теорем [22-26] (см. выделенное курсивом в конце четвертого раздела), частицы Q(CB] в течение некоторого времени будут составлять непрерывные кривые и находиться в G. При этом частица Q(B) покоится (т.к. уже доказано, что Q(B ) = 0 11. следовате.тыю. q(B) = 0).
Предположим, что в точке C выполнено неравенство Q х V = 0. Тогда в точке C скорость q = aQ/p не равна нулю и имеет ненулевую нормальную к линии торможения компоненту. Поэтому если щчастица находится в точке C в момент времени to, то существует такое At > 0, что, двигаясь со скоростью q, эта щчастица покинет линию торможения и в момент времени to + At будет находиться в некоторой точке C‘ внутри замкнутой области G вне линии торможения. Через точку C‘ проходит линия тока, не совпадающая с линией торможения. Расстояние от точки торможения B до линии тока, проходящей через точку С', конечно и положительно (рис. 5). Но это противоречит непрерывности линии, состоящей из частиц Q(CB\ в момент времени to + At, поскольку частица Q(B) покоится и находится в точке B. К этому противоречию привело предположение о том, что в точке С выполнено неравенство Q х V = 0. Поэтому (в силу произ вольности выбора точки С на линии торможения и в силу непрерывности полей завихренности и скорости) на всей линии торможения, включая точки A и B, выполнено равенство Q х V = 0.
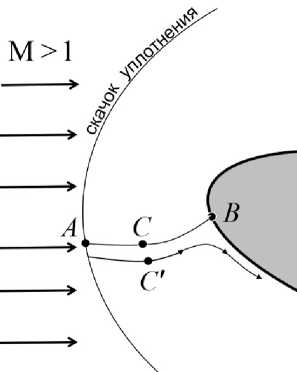
Рис. 5. Расстояние от точки торможения B до линии тока, проходящей через точку С‘, конечно и положительно
Вместе с уравнением (1) равенство Q х V = 0 означает, что во всех точках линии торможения AB градиент энтропийной функции равен нулю (V)cr = 0, в частности, Vcr(A) = 0.
7. Точка начала линии торможения на скачке (основной результат)
Обозначим: A - точка на скачке, в которой касательная к скачку плоскость перпендикулярна направлению набегающего потока (начало лидирующей линии тока за скачком, лидирующая точка скачка). Параметры течения на разных сторонах скачка связаны условиями на косом скачке уплотнения [14, 27]. Из этих условий и из того, что скачок имеет искривленную выпуклую форму, следует, что проекция ^а на поверхность скачка равна нулю только в точке A . В точке A скачок перпендикулярен скорости V(A’). Поэтому, используя уравнение (1), получаем, что проекция Va(A') на нормаль к скачку также равна нулю.
Итак, А - единственная точка на скачке, где Va = 0, а энтропия максимальна на линии тока, начинающейся в этой точке. Выше было показано, что Va(A) = 0. Поэтому точка А совпадает с точкой A. Таким образом, приходим к основному результату.
В течениях с отошедшим головным скачком при обтекании тел с гладкой выпуклой носовой частью линия тормоэюения совпадает с лидирующей линией (то есть начинается там, где касательная к скачку плоскость перпендикулярна скорости набегающего потока), а энтропия принимает максимальное значение на линии тормоэюения и на поверхности тела. При этом завихренность в точке тормоэюения равна нулю.
Полученный результат, в частности, означает, что давление и плотность в передней точке торможения можно вычислять по параметрам набегающего потока с использованием условий Ренкина - Гюгонио на прямом скачке в точке начала линии торможения. Следовательно, при заданных параметрах набегающего потока давление и плотность в точке торможения и энтропийная функция на поверхности тела будут одинаковыми для различных тел, распложенных под различными углами атаки.
8. Заключение
Полученный результат был уже ранее опубликован в [28], где были приведены только основные шаги доказательства. В данной статье приведено развернутое доказательство с обоснованием основных и промежуточных шагов. Важную роль в таких обоснованиях играет раздел 4 «Теоремы об автономных системах обыкновенных дифференциальных уравнений», выводы которого могут использоваться для изучения закономерностей течений в окрестности линии торможения других небаротропных течений (не только для течений с отошедшим скачком уплотнения).
Список литературы Решение задачи Дородницына
- Ладыженский М.Д. Пространственные гиперзвуковые течения газа. Москва: Машиностроение, 1968.
- Крайко А.Н. Краткий курс теоретической газовой динамики. Москва: МФТИ, 2007.
- Матяш E.G., Савельев A.A., Трошин А.И., Устинов М.В. Учет влияния сжимаемости газа в 7-модели ламинарно-турбулентного перехода // Журнал вычислительной математики и математической физики. 2019. Т. 59, № 10. С. 1779-1791.
- Королев Г.Л. Стационарное вязкое обтекание эллиптического цилиндра до чисел Рейнольдса 900 // Ученые записки ЦАГИ. 2012. Т. 43, № 5. С. 46-59.
- Egorov I.V., Fedorov A.V., Palchekovskaya N., Obraz А.О. Effects of Injection on Heat Transfer and the Boundary-layer Instability for a Hypersonic Blunt Body Configuration // International Journal of Heat and Mass Transfer. 2020. V. 149. P. 1-6.
- Чувахов П.В., Егоров И.В. Численное моделирование эволюции возмущений в сверхзвуковом пограничном слое над углом разряжения // Известия Российской академии наук. Механика жидкости и газа. 2021. № 5. С. 49-60.
- Лойцянский Л.Г. Механика жидкости и газа. Москва: Дрофа, 2003.
- Овсянников Л.В. Лекции по основам газовой динамики. Москва-Ижевск: Институт компьютерных исследований, 2003.
- Никольский A.A. Теоретические исследования по механике жидкости и газа // Труды ЦАГИ. 1981. Вып. 2122. С. 1-286.
- Миронюк И.Ю., Усов Л.А. Инвариант линии торможения при стационарном обтекании тела завихренным потоком идеальной несжимаемой жидкости // Вести. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Т. 24, № 4. С. 780-789.
- Анкудинов А.Л. Кинетический ударный слой в плоскости растекания аппарата типа несущий корпус // ПММ. 2021. Т. 85, вып. 5. С. 615-625.
- Ван-Дайк М. Альбом течений жидкости и газа. Москва: Мир, 1986.
- Бэтчелор Дж. Введение в динамику жидкости. Москва: Мир, 1973.
- Мизес Р. Математическая теория течений сжимаемой жидкости. Москва: ИЛ, 1961.
- Prim R., Truesdell С. A Derivation of Zorawski's Criterion for Permanent Vector-lines // Proc. Amer. Math. Soc. 1950. V. 1. P. 32-34.
- Truesdell C. The Kinematics of Vorticitv. Bloomington: IU Press, 1954.
- Фридман A.A. Опыт гидромеханики сжимаемой жидкости. Ленинград-Москва: ОНТИ, 1934.
- Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч. 1. Москва: Физматгиз, 1963.
- Голубкин В.Н., Сизых Г.Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Изв. РАН. МЖГ. 1987. № 3. С. 176-178.
- Марков В.В., Сизых Г.Б. Эволюция завихренности в жидкости и газе // Изв. РАН. МЖГ. 2015. № 2. С. 8-15.
- Сизых Г.Б. Эволюция завихренности в закрученных осесимметричных течениях вязкой несжимаемой жидкости // Уч. записки ЦАГИ. 2015. Т. 46, № 3. С. 14-20.
- Бибиков Ю.Н. Курс обыкновенных дифференциальных уравнений. Москва: Высшая школа, 1991.
- Петровский П.Г. Лекции по теории обыкновенных дифференциальных уравнений. Москва: Издательство Московского университета, 1984.
- Понтрягин Л. С. Обыкновенные дифференциальные уравнения. Ижевск: Регулярная и хаотическая динамика, 2001.
- Денисов A.M., Разгулин А.В. Обыкновенные дифференциальные уравнения. Ч. 1. Москва: Издательство Московского университета, 2009.
- Денисов A.M., Разгулин А.В. Обыкновенные дифференциальные уравнения. Ч. 2. Москва: Издательство Московского университета, 2009.
- Седов Л.П. Механика сплошной среды. Т. 1. Москва: Наука, 1983.
- Sizykh G.B. Entropy Value on the Surface of a Non-Symmetric Convex Bow Part of a Body in the Supersonic Flow // Fluid Dynamics. 2019. V. 54, I. 7. P. 907-911.


