Решение задачи фильтрации при оптимальной настройке радиоотражающего сетеполотна трансформируемого рефлектора

В настоящее время спутники связи активно используются для решения широкого круга задач [1; 2]. Одним из конструктивных способов реализации таких спутников является создание крупногабаритных космических рефлекторов [3–5]. Ведутся активные разработки в этой области. Данные конструкции позволяют работать одновременно в нескольких частотах, обладают большой областью засвечивания [6–9].

Рассмотрим реализацию крупногабаритной космической конструкции с применением вантовой системы для создания необходимой формы радиоотражающей поверхности рефлектора (рис. 1) [10–14]. Крупногабаритный трансформируемый рефлектор (КТР) состоит из космического аппарата (КА) 1 . К нему прикреплены разворачиваемые элементы, такие как солнечные батареи 2 , облучающая система 3 . Для обеспечения заданной диаграммы направленности штанга 4 выдвигает рефлектор 5 на необходимое фокусное расстояние. Отражающей поверхностью является сетеполотно 6 .

Для эффективного использования спутников связи необходимо поддержание точной формы радиоотражающего сетеполотна 6 . Это позволяет обеспечивать качественную диаграмму направленности и высокий уровень сигнала при приёме-передаче данных [15; 16].

Ввиду эксплуатации оборудования в космическом пространстве возникают периодические возмущающие воздействия на конструкцию рефлектора. Такие возмущения вызваны изменением температурного режима, наличием радиации, солнечного ветра [17; 18]. В процессе получения сведения о состоянии формы радиоотражающей поверхности необходимо учитывать влия- ние шумов измерений. Ввиду ограниченности запасов энергии на рефлекторе важным является минимизация энергетических затрат.

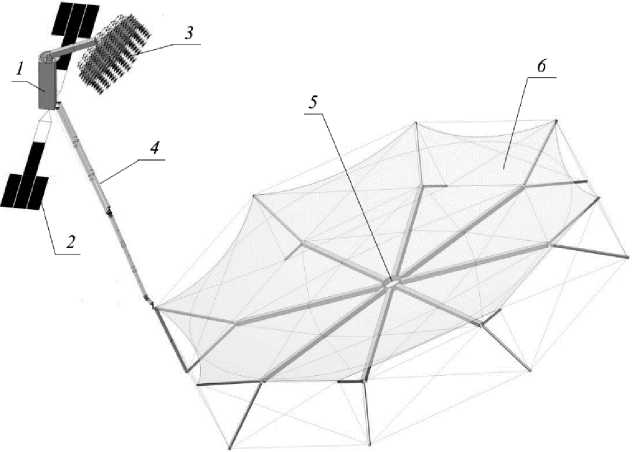
Рис. 1. Конструкция крупногабаритного трансформируемого рефлектора

• Fig. 1.    The design of the LTR (Large-sized transformable reflector)

Таким образом, необходимо осуществить точечную поднастройку сетеполотна при минимизации энергетических затрат, учитывая влияние шумов измерения и внешних возмущающих воздействий.

Математическое описание задачи

На рис. 2 представлена одна спица КТР в сечении, где 1 – спица, 2 и 3 – внешняя и задняя сетка, 4 – ванты, в которых установлены актюаторы. Необходимо, изменяя длину вант 4 с помощью актуаторов 5 , задать желаемую форму радиоотражающего сетеполотна 2 , обеспечив тем самым требуемую диаграмму направленности. В качестве актюаторов рассматривался пьезопривод. Желаемая форма задаётся в наземных условиях. В процессе доставки КТР на заданную орбиту и при раскрытии конструкции может происходить незначительное смещение реальной формы от желаемой. После развёртывания происходит сверка контрольных точек и на актюаторы 5 передаётся управляющее воздействие для изменения длины ванты 4 .

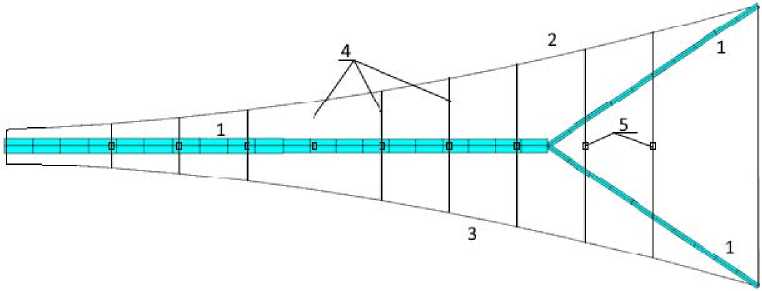
Рис. 2. Спица в сечении

• Fig. 2.    The spoke in cross section

В качестве актюатора для управления настройкой радиоотражающего сетеполотна выбран пьезоактюатор типа АПМ [19] с перемещением l max = 10 мм при допуске перемещения ±15 %. Для измерения напряжения на входе пьезоактюатора взят преобразователь напряжения измерительный ПИН-50-У-4/20-ДХ [19] с основной приведенной погрешностью не более 1,5 %. Для измерения изменения длины ванты используется лазерный сканер RangeVision Standard Plus [21] с точностью ±0,03 мм.

Система дифференциальных уравнений, описывающих пьезоэлемент с исполнительным органом на основании выводов А. А. Никольского [22], имеет вид X = f(X, u, t) + ξx, где X = (l V Uэ)T – вектор состояния, ξx = [ξx1 ξx2 ξx3]T – шум с интенсивностью Bx = diag(Bx1, Bx2, Bx3). Или в поэлементном виде l = V + ^ x 1,

. NKU + F - KJ - KV

V =        ----c----у----- _{Д +} ^ x 2 ,                                   (1)

mE eэ        Uэ     KпV

U, —+ ^,. , ^э C 0 R вт K д C 0 R вт K д C 0 K д    ^{x 3}

где l – изменение длины (ход) актюатора; V – скорость выдвижения актюатора; N – количество элементов; K 0 – коэффициент обратного пьезоэффекта; U э – электрическое напряжение, приложенное к электродам актюатора; F c – статическое усилие; K у – коэффициент упругости; K д – коэффициент внутреннего демпфирования; e э – напряжение от источника электродвижущей силы; C 0 – ёмкость; R вт – внутреннее сопротивление; K п – коэффициент прямого пьезоэффекта; m Σ – суммарная масса, состоящая из массы самого пьезоактюатора и перемещаемой массы.

Общепринятая на практике постановка задачи совмещенного синтеза оптимального управления линейными системами опирается на теорему разделения. Согласно этой теореме, оптимальная система управления состоит из оптимального фильтра, формирующего оценки вектора состояния системы, и оптимального регулятора, определяющего управление уже в детерминированной постановке при предположении, что вектор состояния известен точно [23–25]. В данной статье для построения управления применяется фильтр Калмана и алгоритм последовательной оптимизации [26].

Измерению доступны длина выдвижения и напряжение на пьезоактюаторе. Уравнение наблюдения рассмотрим в виде

Z — H x + § _z ,                                         (2)

где z = [ z 1 z 2 ]^T, H = [1 0 1]^T, ξ z = [ ξ z 1 ξ z 2 ]^T – случайные процессы типа белого шума с интенсивностью B z = diag ( B z 1 , B z 2 ).

Оптимальную оценку можно получить с помощью фильтра Калмана

— V + R_n в ;, ( z , dt

^\

- l ) + R,3Bz 2 ( z2 - Uэ ), dV dt

NK ₀ U _э + F _c - K у l - K _д V

m E

+ R 21 B_Z1

Z,

l ) ^{+ R} 23 ^Bz 2 ( z 2

U ^ˆ э

,

dU ^ˆ _э dt

e _э

C 0 R вт K д

U ˆ э      K п V

C 0 R вт K д   C 0 K д

+ R 31 в ;,

z ₁

^\               1

l ) ^{+ R} 33 ^Bz 2 ( ^z 2

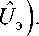
R — AR + RAT - RHTB- 1HR + Bx, R (10) — R0, где

А =

0	i	0
K у	K д	NK 0
m Е	m Е	m Е
0	K п	i
	C 0 K д	C 0 R вт K д

, Rnn ( t0 )   9^хп, остальные элементы матрицы начальных ковариаций ошибок оценивания принимались равны ми нулю.

Постановка задачи управления

Для решения задачи управления применяется алгоритм оптимального управления по иерархии целевых критериев [26]. Помимо выполнения терминальных условий необходимо уменьшить энергетические затраты. Для случая управления пьезоактюатором - это мощность, выделяемая на пьезоактюаторе в процессе управления.

Управление вычисляется в виде и = и _i + и ₂, где и _i и и ₂ минимизируют критерии качества J _i и J 2 соответственно

Ji = Vf i(X, tf ), tf

J2 = Vf2(X,tf ) + j[f,(X,t) + 0,5(и2 + и2)2к22]dt , t 0

где V fi = 0,5p i [ V ( t f ) - V f ]², Уд = 0,5A X f T p к A X f ; f , = 0,5в 2 [ l ( t ) — l f ]² + 0,5в з P э ( t ); P к = diag (p i , p₂, р з , Р д ), Рь в 2 , в 3 , к 2 — заданные коэффициенты; A X f = X ( t f ) - X f , X f = ( l f V f U э f )^T - заданное конечное значение вектора X в (i), Р э = U п • I = ( e э - U э ) ² / R вт - электрическая мощность; U _п - полное приложенное напряжение; I - ток. Подробно решение задачи управления в детерминированной постановке рассмотрено в работе [22].

Для оценки влияния возмущений на систему необходимо определить величины внешних возмущений и шумов измерений. Помимо внешних возмущений может наблюдаться изменение начального и конечного состояния, вызванное воздействиями на конструкцию при доставке рефлектора на орбиту.

Примем, что отфильтрованный шум измерений не превосходит ошибок измерительных датчиков. Внешние возмущения (влияние нагрузки, температуры окружающей среды, солнечное давление, радиация и т. п.) оказывают воздействие на весь вектор переменных состояния. Как правило, внешние возмущения случайны, некоррелированы и распределены равномерно в заданном диапазоне. В космическом пространстве внешнее влияние, оказываемое на рефлектор, является достаточно длительным и медленно нарастающим, поэтому на рассматриваемом интервале времени (не более i0 с) его можно считать квазистационарным. Возмущения примем равными ±i % от максимальных значений соответствующих переменных. В общем случае величины возмущений от нештатных ситуаций предугадать затруднительно.

Пьезоактюатор выдвигается из начального положения при значении l 0 = 0 мм и фиксируется при достижении заданной длины l f = 5 мм. Актюатор в начальном положении находится в состоянии покоя, соответсвенно линейная скорость V 0 = 0 м/с, напряжение U э ₀ = 0 В. Конечное значение линейной скорости V f = 0 м/с. Пьезоактюатор преобразует электрическое напряжение в механическое перемещение [i9]. Когда к нему приложено электрическое напряжение, он деформируется, при снятии напряжения он приходит в исходное состояние. Примем конечное значение напряжения, исходя из ограничений, принятых на орбите U э f = i2 В. Время выдвижения t f = 4 с.

Моделирование

Для моделирования был выбран тонкопленочный пьезоэлектрический микроактюатор типа АПМ со следущими техническими характеристиками [19]: K 0 = 3,425∙10^–8 Кл/м, m Σ = 0,125 кг, F c = 0 Н, K у = 7,611 Н/м, К д = 1,9, С 0 = 11,7∙10^–5 Ф, R вт = 1,025∙10² Ом. Для осуществления выдвижения на заданную длину l f = 5 мм при ограничении на управление e э max = 12 В необходимо N = 305 слоёв.

Численное моделирование перевода системы из начального состояния x (0) = (0 0 0)^T в конечное x ( t f ) = ( l f 0 U э f )^T при минимизации энергии P э с отсутсвием перерегулирования по длине выдвижения l за время t f = 4 с проводилось методом Эйлера с шагом Δ t = 0,00001 с. Расчеты показали, что при значениях параметров критерия J 2 : ρ 1 = 10⁴, ρ 2 = 10⁸, ρ 3 = 0, ρ 4 = 0, β 1 = 0, β 2 = 0, β 3 = 0, k 2 = 1 алгоритм успешно решает поставленную задачу. Затраченная мощность на перевод системы из начального в конечное положение P _э = 0,0075 Вт, при максимальном токе I = 0,0069 А.

На рис. 3 представлены результаты моделирования, графики зависимостей l ( t ) и V ( t ) соответственно. Видно, что удалось решить поставленную задачу, т. е. перевести пьезоактюатор из начального состояние в конечное, переместив его активную часть на 5 мм при B x = diag (0,00075, 0, 0,12, 0).

На рис. 4 представлены ток и мощность при работе пьезоактюатора. Видно, что за время моделирования было затрачено около 8 мВт.

Принятые возмущения и шумы измерений не оказывают существенного влияния на переходные характеристики системы. Алгоритм успешно справляется с возмущениями и отклонениями начальных значений в диапазоне ± 10 %.

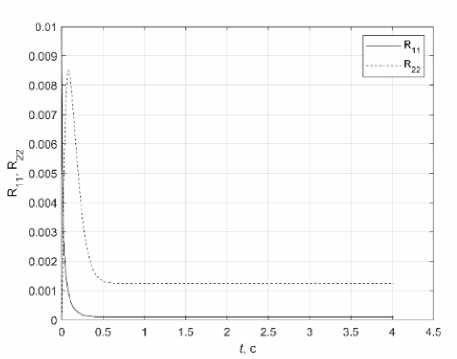
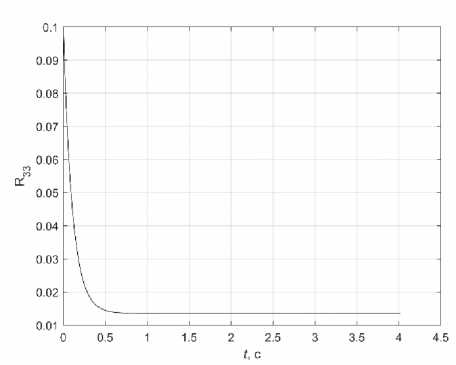
На рис. 5 представлены диагональные элементы матрицы ковариации при R 11 (0) = 0,01; R 22 (0) = 0,001; R 33 (0) = 0,1; B z = diag (0,0001, 0,18). Видно, что с течением времени они приходят к установившимся значениям. Также было проведено моделирование при разных уровнях шума. Фильтр Калмана отрабатывает их успешно.

Поскольку шумы измерений не оказывают сильного воздействия на управление, то для экономии энергии было предложено периодически отключать работу датчиков и текущее положение определять путем математического моделирования. Это позволило успешно решать задачу управления при меньших энергетических затратах. В моменты отключения датчиков не затрачивается энергия на их функционирование и передачу данных.

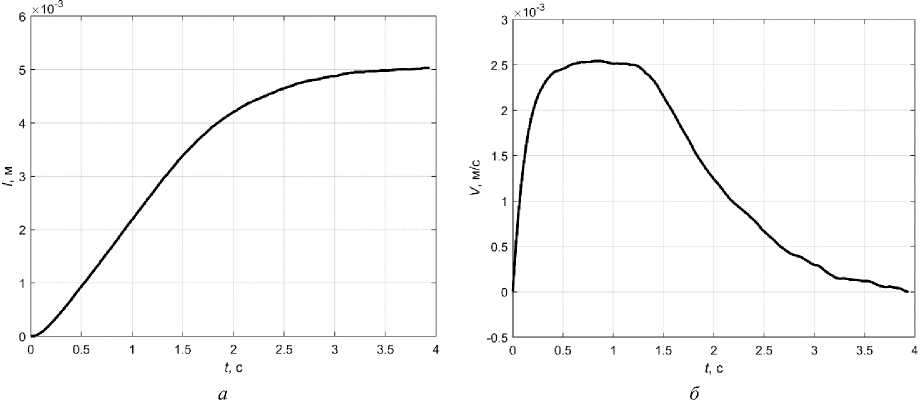
Рис. 3. Графики: a – l ( t ); б – V ( t )

Fig. 3. Graphics: a – l ( t ); b – V ( t )

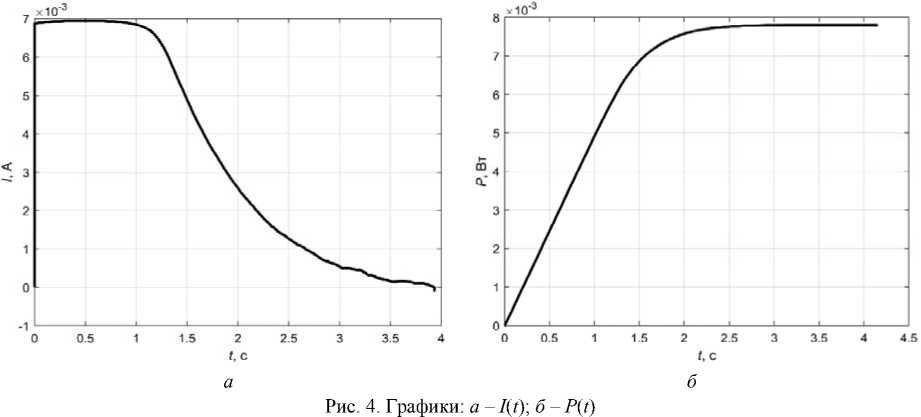
Fig. 4. Graphics: a – I ( t ); b – P ( t )

а

б

Рис. 5. Графики: а – R ₁₁( t ), R ₂₂( t ); б – R ₃₃( t )

Fig. 5. Graphics: a – R 11 ( t ), R 22 ( t ); b – R 33 ( t )

а

б

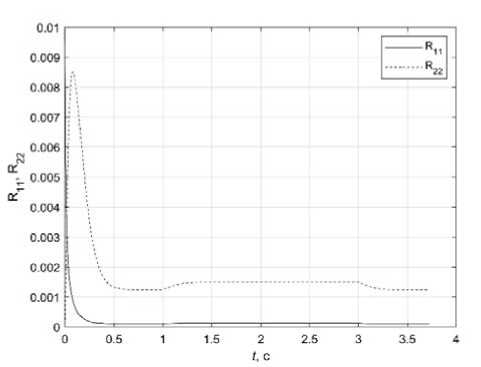
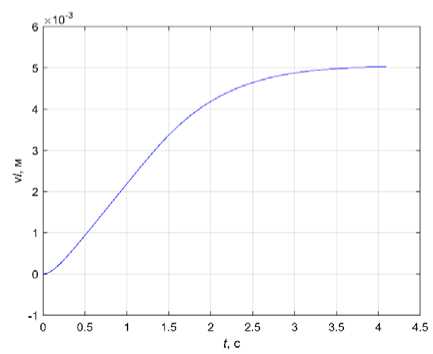
Рис. 6. Графики: а – R ₁₁( t ), R ₂₂( t ); б – l ( t )

Fig. 6. Graphics: a – R 11 ( t ), R 22 ( t ); b – l ( t )

На рис. 6, а представлены графики R 11 ( t ) и R 22 ( t ) при отключении измерений с 1 до 3 секунды. Рис. 6, б показывает оцененную величину l ( t ). Элементы ковариационной матрицы приходят к установившемуся значению при наличии наблюдений. На интервале отключения измерений при B Z1 = 0 и B z2 = 0 величины оценок и R ц( t ), R 22 ( t ) вычисляются с помощью фильтра в режиме прогноза.

При включении измерений на 3 с фильтр Калмана приводит оценку к оптимальному значению к 3,2 с. Математическое ожидание шума равняется нулю, поэтому при отключении измерений каких-либо существенных отличий в оценке измеряемых величин не наблюдается. Критическим является наличие внешних возмущений, так как за время отключения датчиков возможен уход математической модели от состояния реальной системы. Ввиду того, что процесс управления для рассматриваемой задачи занимает t f = 4 с, важно включать измерения при приближении к конечным значениям, что позволит оценить состояние системы и при необходимости скорректировать управление. При этом достаточно проводить измерение длины выдвижения пьезоактюатора l , включение датчика измерения напряжения U э0 = 0 незначительно повышает точность решения задачи.

Ошибки оценивания Δ l и Δ U э при работе фильтра Калмана с течением времени стремятся к нулю. При наличии внешних возмущений данные ошибки имеют математическое ожидание равное нулю и дисперсию, не превышающую дисперсию возмущений.

Заключение

Для решения задачи управления также применялись алгоритмы на основе принципа максимума Понтрягина с использованием численных методов Ньютона, Крылова – Черноусько, алгоритма коррекции параметров структуры управления [12; 23; 27]. Алгоритм последовательной оптимизации позволил на 12 % снизить энергетические затраты на управление. Применение ПИД-структуры управления увеличивало затраты электроэнергии на 27 % по сравнению с предлагаемым алгоритмом [28] при наличии перерегулирования.

Как видно, численное моделирование подтвердило возможность решения задачи оптимального управления стохастической моделью пьезоактюатора для настройки радиоотражающего сетеполотна КТР по неполным данным с использованием принципа разделения. Интервальное выключение измерений позволяет снизить энергозатраты на питание датчиков и обработку измерений. При этом более длительное включение датчиков в конечный момент времени приводит к более точному выполнению терминальных условий. Поэтому дополнительно возникает задача оптимизации интервалов наблюдения с целью минимизации энергетических затрат при высокоточном выполнении терминальных условий [29].

Представленные исследования доложены на XXII международной научной конференции «Системный анализ, управление и навигация» [30].