Решение задачи идентификации на основе дифференциального преобразования

Проблема идентификации в последнее время становится исключительно важной в связи с необходимостью повышения качества процессов управления. Известно множество подходов к этой проблеме, например, идентификация на основе сплайн-аппроксимации [1]. Одним из этапов идентификации линейных систем во временной области является аппроксимация временных функций и конструирование на их основе передаточных функций. Аппроксимация временных характеристик проводится в такой последовательности: составление характеристических уравнений, определение корней и решение вспомогательных уравнений, где неизвестными считаются коэффициенты экспоненциальных многочленов, аппроксимирующих временные функции [2-4]. Эти этапы аппроксимации различны для разных классов систем и поэтому трудно алгоритмизируемы.

Цель работы - решение задачи идентификации дробно-рациональных передаточных функций систем на основе аппроксимации временных характеристик с использованием дифференциального преобразования [5].

Дифференциально-тейлоровское преобразование, предложенное и изученное Г.Е. Пуховым нашло применение в задачах математического моделирования, где решение уравнений на заданном интервале изменения независимого переменного эффективно может быть представлено степенными рядами Тейлора:

»к L

к=0

к

где слева от символа <—> стоит прямое преобразование оригинала x(t) в изображение Х(к) - дискреты дифференциального спектра, а справа - обратное преобразование Х(к) в x(t), к - дискретный аргумент, t - время, Н- некоторая постоянная.

Например, изображающая функция для оригинала х(0 = е"' равна kl[ dtk J(_o к'.                     '

Дискреты функции XQt\ изображающей экспоненту e', равны X(0) = l, XQ} = -H,

X(2) = H212\, А(3) = -Я3/3! и т.д. Совокупность этих дискрет образует дифференциальный спектр экспоненты е' (рис. 1). По дифференциальному спектру экспоненту можно легко восстановить:

V t у (-н)^к . г² t

-— ------— 1 — ? нн к'.2! 3!

Согласно свойству связи с преобразованием Лапласа:

0                       к=0 Р "

Для переходной характеристики x(f) можно записать:

К(р) = pIW)A = X =< где %№ = к\Х{к)! Нк, р = jm, оз- угловая частота. Из выражения (2) следует, что К(р) представима бесконечным рядом. Для получения К(р) в виде дробно-рациональной функции

K()=jwyl^ii^^ f3)

Р +<ЧР + а_гр + ... + а„ ряд следует ограничить. Так как вся информация о свойствах линейных систем и-го порядка вида (3) содержится в первых 2и коэффициентах ряда (2), то для получения Др) в виде (3) достаточно найти только 2и дискрет спектра временной функции [4]. Для этого, в случае таблично или графически заданной временной функции (рис. 2, а) составляем систему линейных уравнений:

§АО) = х(/„)-х(0);

7=1

< ™ ( t У                                     (4)

i = 1, т -1, t, = iM, Xt = HI m,t_m = mX, где m > 2n , и, решая её, находим дискреты степенного многочлена, аппроксимирующего данную временную функцию. Согласно формуле (2) по найденным дискретам из (4) получаем К(р) в виде ряда. Для получения К(р) в виде (3) используем способ нахождения дробей, соответствующих рядам [3]. Как и в работе [1] будем считать, что система имеет передаточную функцию, вид которой известен, т.е. известен порядок числителя и знаменателя передаточной функции, но неизвестны коэффициенты.

С помощью системы линейных уравнений и-1                                  _______

£ Х(г’ + JX-, =-Х(п + A j = 0, п -1(5)

(=0

определяем коэффициенты а„, а из уравнений р>о =х(0);

• -                                     (6)

bj = Х(У) + X ^aiXU-*Х j = Vn-1

.1=1

находим коэффициенты b„ дроби (3).

Количество рассчитанных дискрет, которое используется при восстановлении решения в виде ряда Тейлора, является одним из наиболее существенных "              Вестник ЮУрГУ, № 23, 2007

факторов, влияющих на точность. Чем больше дискрет будет вычислено, тем более точным будет полученное решение, так как оно будет представлять более полный ряд Тейлора. Реальные условия всегда ограничивают максимальное количество вычисляемых дискрет объемом памяти, предназначенным для хранения значений, либо временем вычислений. Таким образом, из-за ограничения количества рассчитываемых дискрет возрастает ошибка самого метода. Таким образом, для реальных расчетов принципиально необходима оценка точности.

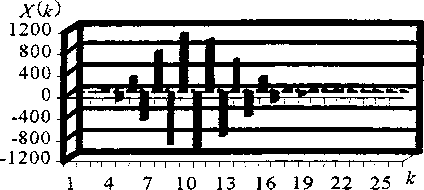
Рис. 1. Дифференциальный спектр Экспоненты при Н = 9

Численное моделирование показывает, что увеличение числа дискрет приводит к уменьшению отклонения решения на всем интервале, причем максимальное отклонение всегда приходится на конец интервала. Из этого вытекает, что среднеквадратическое значение погрешности всего решения будет не выше данного значения. Согласно свойству дифференциального преобразования, изображение конечного значения оригинала при t = H равно сумме дискрет изображения оригинала. Отсюда следует очевидное равенство:

х(Н) = ^ ад = ^ВД + г(л + 1),

А=0         к=0

где г (и) = ^Х(к).

к-п

Учитывая знакопеременность дифференциального спектра, можно предположить, что отклонение решения при t = Н по абсолютной величине будет не больше самой старшей рассчитанной дискреты:

|г(и + 1)|<|йГ(и)[.

Тогда верхнюю границу погрешности можно определить исходя из величины последней дискреты следующим образом:

RW = \X^\ ^Х^.

7 к=0

Полученный критерий является довольно грубым, но позволяет быстро оценить погрешность полученного решения при заданном количестве дискрет на текущем интервале времени. Более точную оценку погрешности можно получить, если сравнивать между собой решения, полученные для и и п+т дискрет:

• —£¹ —z-----; >  *1^е [°-•

х(/,,и + т)

Математическая строгость требует сравнения значений этой погрешности для m = 1, 2, 3,... до тех пор, пока соответствующие значения R(n,m) не будут совпадать с требуемой точностью. При таком использовании данный критерий довольно трудоемок, так как кроме двойного расчета решения он требует еще и дополнительного расчёта т дискрет Ди+1), Ди+2),.„, Ди+м).

Погрешность восстановленного решения существенно зависит от временного интервала, на котором оно восстанавливается. Поскольку дискреты фактически представляют собой слагаемые степенного ряда (1) в точке t = H, по дифференциальному спектру можно судить о сходимости ряда (1) на интервале Г = [0...Я]. Известно, что, если ряд сходится в точке t = Н, то он сходится на всем интервале Т. Если последние дискреты спектра являются убывающими и их величина достаточно мала по сравнению с суммой, то можно говорить о сходимости ряда. Если спектр не является убывающим с некоторой дискреты, то решение расходится на данном интервале. В таком случае требуется увеличение количества дискрет, либо уменьшение интервала.

По дифференциальному спектру можно не только судить о сходимости, но также и оценить точность решения при заданном количестве дискрет, либо наоборот, оценить количество дискрет, требуемое для достижения заданной точности решения на интервале Т = [0...Я]. Наибольшее отклонение решения оказывается в конце интервала при t = Н . Тогда для достижения абсолютного отклонения решения в конце интервала менее R_H необходимо, чтобы величина последней дискреты была меньше заданной величины R_H.

Для линейных устройств при любом значении Н всегда найдется такой номер дискреты п, для которого выполняется условие |У(и + Л)| <  R_H, к = О, 1,2... Это означает, что при достаточном количестве дискрет решение может быть построено на любом интервале. Данное утверждение можно доказать следующим образом. Решение линейного дифференциального уравнения есть сумма экспонент. В дифференциальной форме выражение для расчёта дискрет спектра экспоненты выглядит как ХЦс^сНУ/к'., или в рекуррентной форме: Х(к) = Х{к~\)сН/к . Для того, чтобы значение дискреты Ди) достигло требуемого малого значения R_H, необходимо и достаточно, чтобы дифференциальный спектр стал убывающим с некоторой дискреты т, то есть \Х(к + т )|<|Х(^ + ш-1)|. Для этого необходимо и достаточно, чтобы множитель сН/к был меньше единицы. Иначе говоря, дискреты начнут убывать при к > |сЯ|. Следовательно, всегда найдется такое и, что |(сЯ)”/и!|< R_H . Оче-

Серия «Компьютерные технологии, управление, радиоэлектроника», выпуск 6          g^

видно, что с увеличением значения Н при расчете дискрет увеличивается и номер п.

Таким образом, широкое использование дифференциальных преобразований напрямую зависит от уровня развития вычислительной техники. Существенный прогресс в этой области, появление мощных компьютеров и программного обеспечения уже в настоящее время вновь позволяет вернуться к вопросу о применении дифференциальных преобразований для исследования систем.

В качестве примера рассмотрим экспоненциальный полином [3]:

КА = 1,992е'^0>779' - е'°¹⁵⁸⁴' х

х(0,992 cos(l, 340 - 0,39sin(l,34r)),          (7)

построенный по значениям функции КО ^е (С 0,95; 1; 0,942; 0,75; 0,491; 0,25; 0,083; 0}, t = М с, с шагом 0,5 с. Используя преобразование Лапласа, найдем передаточную функцию этого полинома:

ад- /^/-^ . (8)

/+1,947/+3,047^ + 1,665

Найдем передаточную функцию, используя дифференциальное преобразование. Для этого решим систему (4), зная значения функции в узлах интерполяции, и при Н= 4 найдем дискреты спектра X(k) е {1; -1,85; 17,35; -52,27; 51,6; 1,18; -35,31; 23,3; -5}, к = 0,8. Используя только 2л = 6 первых дискрет с целью получения передаточной функции третьего порядка, находим:

^НЩМ«^ (9)

р³ + 2,082/ +2,835^ + 1,698

Если взять в два раза меньшее число значений функции КО (^с шагом 1), то по дискретам спектра Х(к) е {1; -1; 13,02; -52,08; 65,1; 1; -26,04}, получим передаточную функцию:

ад- г^ададР

/+1,615/+1,697^ + 1,157

Амплитудно-частотные характеристики К^вО =|K(p)| для формул (8)—<10) изображены на рис. 2, б. Малая ошибка аппроксимации ^(со) функцией К_г (ю) (максимальное отклонение 5 %) по сравнению с ^(ш) - 35 % объясняется большим числом взятых значений временной функции при одинаковом числе дискрет. В случае увеличения числа отсчетов временной функции и, следовательно, возможного в связи с этим повышения порядка передаточной функции, можно повысить точность аппроксимации.

Существенное повышение точности достигается в случае, если (2) представить суммой бесконечно убывающей геометрической прогрессии с первым членом с₀ = %(0) и знаменателем q. Передаточная характеристика системы может быть найдена по формуле:

ад=с0/а-?)               ап без аппроксимации (4)-(6). Например, если

A(0 = cos(VVa),                       (12)

то для нахождения Цр) (12) представим в виде

КО = l/2^exp(yr/Va) + exp(-j/Va)^, и найдем дискреты спектра

X(k) = Нк/2к\ (j/^ +(-}/^к .

По формуле (2) найдем выражение к=0 2рк№ ра ра которое представляет собой бесконечно убывающую геометрическую прогрессию для с0 = 1 и q = -\l(p2a) ■ Используя (И), получаем: К(р) = р2а1(\ + рМ ■

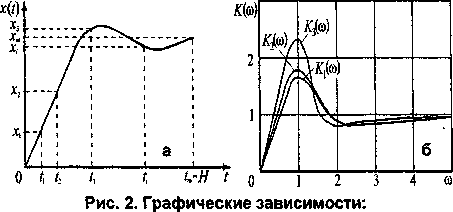
а - аппроксимация временных характеристик; б - передаточные функции (8)—(10) экспоненциального полинома (7)

Следовательно, имея все дискреты временной функции, по соотношению (11) можно получить точную передаточную характеристику.

Рассмотренная методика идентификации передаточной функции легко алгоритмизируется, и её можно использовать в программах синтеза линейных систем.