Решение задачи моделирования систем технического обслуживания летательных аппаратов

The basic parameters and characteristics of the uniform information system of support maintenance and technical operation offying devices under operating conditions both on the appointed resource and on a condition are offered.

Н. В. Никушкин, А. В. Кацура

РЕШЕНИЕ ЗАДАЧИ МОДЕЛИРОВАНИЯСИСТЕМ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ

Представлено краткое описание марковской модели нерезервированных агрегатов и систем! летательных аппаратов срегламентным техническим обслуживанием.рассмотрены особенности ее численногорешения.

В работе [1] рассмотрены марковские модели технического обслуживания (ТО) агрегатов и системы летательных аппаратов (ЛА), на которых в процессе эксплуатации проводится ТО с определенной периодичностью и объемом. Модель нерезервированных агрегатов и систем летательных аппаратов с регламентным техническим обслуживанием (РТО) представлена ниже (рис. 1).

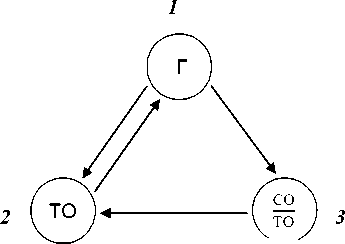
Рис. 1. Граф состояний нерезервированных агрегатов с регламентированным ТО [1]: 1 - готовность к работе (Г); 2 -регламентированное техническое обслуживание (ТО);

CO

3 - скрытый отказ ( то )

Состояние 2 может соответствовать проведению на агрегате и других видов ТО: еженедельного, ежемесячного, ежеквартального, однако ориентированный граф от этого не изменится.

Вектор X совокупности эксплуатационных характеристик (ЭХ) ЛА для рассматриваемой модели включает три характеристики: ш - параметр потока отказов нерезервированного агрегата с РТО; Т_мто - периодичность РТО; Т - продолжительность при очередном РТО.

В процессе эксплуатации агрегат может перейти из состояния готовности к работе 1 в состояние скрытого отказа 3 (переход 1-3). Эти отказы будут выявлены при очередном РТО (переход 3-2). В состояние 2 агрегат переходит с определенной периодичностью Тмто (переход 1-2). После окончания РТО продолжительностью Т , в ходе которого устраняются все обнаруженные отказы и проводится ряд профилактических мероприятий и про верок, агрегат возвращается в состояние готовности к работе (переход 2-1).

Анализ возможных переходов (см. рис. 1) показывает, что если интенсивности переходов а12, а21 и а13 могут быть получены с использованием оценок параметров Т*мто, Т*то и to' по результатам испытаний в виде а12 — Т м.т.о, а21 ~ Т т.о, а13 ~ ®т.о, то интенсивность перехода а32 таким образом получить невозможно.

Для нахождения интенсивность перехода а32 используются свойства марковского процесса с непрерывным временем интенсивности перехода ауи вероятности перехода Р. из ei-го состояния в е.-е состояние и условной функцией распределения времени пребывания F.(t) в е.-м состоянии, тогда

-Г . (^Т. , (V. .' О). ) ") '.

Система дифференциальных уравнений для ориентированного графа состояний (см. рис. 1) имеет вид dP. (t)

d   = "^(а12 ^{+ а}13^{) P}1^{(t) + а}12^Р2^(t) ,

dP (t)

-а 12^p1 (t)-а 21^p2 (t) + а з2^pз (t) ^,        (1)

dP (t)

-«1з^p1 (t)-а з2^pз (t).

Используя преобразования Лапласа, переходят от системы дифференциальных уравнений к системе алгебра- ических уравнений, что позволяет получить выражение для вероятностей Р/t) (при начальном условии Р1(0) = 1), однако окончательные выражения для вероятностей P(t) достаточно громоздки, что вызывает определенные трудности при их анализе.

В стационарном режиме эксплуатации (t ^ ^) система уравнений (1) вырождается в систему алгебраических уравнений

(а1/'а1,)Р|'а.Р/0- а12р1-а21р2 + а32р3-0, (2)

а 1з^Р1 -а з2^Рз ^ ⁰ .

Исследование стационарных режимов эксплуатации нерезервированных агрегатов с РТО осуществляется решением системы (2) при условии нормирования 3

У Pi = 1и исключения избыточного уравнения. Полу- i =1

ченные выражения для вероятности Р1 нахождения агрегата ЛА в готовности к работе и вероятностей переходов Р2 и Р3 имеют вид [1]

(х-1 т1

— + щт.о(т о + т. о) + e""^"

Тц.т.о

Р 2 =

( 1 = Ч.оУт.о

т , ц.т.о

° + ® т.о ( ^т т.о ■ ^т .. ) ⁺ е _v ¹ ц.^т.о

, -“ т.о^.т.о

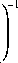
Р 3 =

е “^v™ + щ т ^-1 ______________ т.о ц.т.о

+ щт.о (т о +ти^о) + е"то ц.т.о

.

В выражениях (3)^(5) для более компактного вида применена свертка выражений, учитывающая время ожидания перехода, в экспоненциальной форме. Согласно свойству марковского процесса [2; 3] с непрерывным временем, полная вероятность перехода Руиз е.-го состояния в е-е состояние за время t равна

t

Р / = /Ш 1 - Q k ( * ) ] dQ u ( * ) .         (6)

Подставив в (6) независимые функции распределения Qi/ (t) = 1 - е aij времени ожидания перехода, имеющие для марковских процессов экспоненциальное распреде ление, получают выражение для вероятности перехода:

a

^P/ ( t ) = ~ ( 1 - е~ a i t ) .                 (7)

ai

Используя в решении системы (2) выражение (7), получают окончательные уравнения (3)...(5) вероятностей Р . .

Нетрудно видеть, что эти аналитические выражения не позволяют провести анализ влияния параметров системы ТО на ее показатели, поэтому решение уравнений (3)^(5) заменяется их численным решением, тем более что для более сложных систем уравнений получение аналитических выражений представляет определенные сложности.

Однако при всей компактности и элегантности представленных выше выражений расчет по ним дает завышенные результаты Р₁ вероятности нахождения агрегатов и систем ЛА в готовности к работе, так как выражения для времени ожидания Q в экспоненциальной форме представляют собой теоретический предел и задают закон изменения Р . вероятностей переходов.

Для оценки стационарных режимов эксплуатации (t ^ ^) величины вероятности Р1 нахождения агрегата в состоянии готовности к применению по экспериментальным данным удобнее оценивать непосредственной подстановкой экспериментальных значений в систему алгебраических уравнений.

Разница между результатами расчетов по выражениям (3)^(5) и непосредственной подстановкой экспериментальных данных рассчитываемых параметров по величине вероятности Р1 нахождения агрегата в готовности к работе, например для короткого периодичного регламентированного ТО, составляет

4 % длятто = 2- 10 ч,

Щ ^10⁴, аАт -от25% до 37% (т. е. от380 до 830 ч), т.о м.т.о

• 8,7 % для т_то = 2 -10 ч, ю_то= 10^-5,

а Ат - от 3% до 50 % (т. е. от 70до 2 200 ч), м.т.о что для отдельных видов и форм ТО является временем очередного или межрегламентного времени обслуживания агрегатов и систем. Таким образом, анализ модели системы ТО целесообразно проводить по результатам совместного решения выражений (3)...(5) и системы алгебраических уравнений (2).

Результаты решений вероятности Р1 нахождения агрегата в готовности к работе по (3) для РТО с частым проведением и короткой продолжительностью (для ежедневных, еженедельных, ежемесячных, ежеквартальных, полугодовых ТО) по уравнениям (3)...(5) и прямым численным решением представлены на рис. 2...7, дляРТОс длительной продолжительностью (годовые и более ТО агрегатов и систем ЛА) на рис. 8, 9.

Начала переходных процессов при численном решении алгебраических уравнений (2) смещаются влево и протекают более круто (интенсивно).

Различие в результатах расчета дает возможность провести оценку величины времени на ТО и резервов для качественного совершенствования процесса ТО.

Дополнительно в табл. 3.15 [1. С. 57] допущена техническая неточность. Для модели резервированных агрегатов и систем ЛА с периодическим контролем их ТО в формуле условной интенсивности перехода а56 - перевода агрегата с двумя отказавшими каналами на контроль -выражение интенсивности должно иметь вид а56^(0,5 Тм.п.к-(2Щп.к+Тм.п.к)’1)’1-