Решение задачи о коммивояжере методом целочисленного программирования. Метод ветвей и границ

student

4th course, faculty of information systems and technologies

Volga region state university of telecommunications and informatics

Russia, Samara

student magistracy, department of a postgraduate study and magistracy

Volga region state university of telecommunications and informatics

Russia, Samara

DECISION OF THE TRAVELLING SALESMAN PROBLEM BY METHOD OF INTEGER PROGRAMMING. BRANCH AND BOUND METHOD.

Annotation: In article, the method of integer programming for the solution of a travelling salesman problem is considered. The program is based on a method of branches and boundaries is realized. Assessment of program applicability of a method, speed of its operation and complexity of implementation is made. The example of result of a program runtime is given.

Целочисленные задачи – это задачи, в которых переменные могут принимать только целые значения (или некоторые целые значения).

Задача коммивояжера – важная задача транспортной логистики (отрасль, занимающаяся планированием транспортных перевозок), заключающаяся в поиске наиболее выгодного маршрута (по стоимости переезда, по длине пути и т.п. или совокупности критериев), проходящего через каждый город ровно один раз с последующим возвратом в исходный пункт. Входными данными для такой задачи являются меры выгодности маршрута и соответствующие матрицы расстояний (или стоимости, времени в пути и т.п.). Существует несколько частных случаев постановки задачи коммивояжера, в нашем случае это геометрическая задача, когда матрица на входе является матрицей расстояний, сформированной из координат расположения городов на плоскости.

Выделяют следующие методы решения задачи коммивояжера:

• •    Простейшие методы (методы, включающие полный перебор, а также упрощающие его)

• •    Метод ветвей и границ

• •    Метод эластичной сети

Первая группа простейших методов – это группа эвристических методов, которые, хотя и достаточны для решения поставленной задачи, однако не могут обеспечить высокую точность и оптимальность решения. В таких методах, как правило, находится лишь приближенное решение.

Метод эластичной сети известен тем, что приходит к точному решению, однако для этого ему требуется осуществить большое количество итераций, что для больших задач может негативно сказаться на времени их программного решения.

Рассмотрим решение задачи коммивояжера методом ветвей и границ, который позволяет находить оптимальные или приблизительные решения для достаточно больших задач. В основе этого метода лежит идея последовательного разбиения множества допустимых решений.

В начале определяется некоторое допустимое решение (допустимый маршрут), после чего множество всех оставшихся маршрутов разбивают на подмножества и при каждом разбиении производится анализ подмножеств на содержание ими оптимального решения. Если, как в нашем случае, рассматривается задача на минимум, то сравнение производится путём вычисления так называемой нижней границы целевой функции текущего наилучшего маршрута. Используя найденные границы, проводится дальнейшее разбиение подмножеств допустимых маршрутов, и в результате определяют оптимальный маршрут. Это разбиение подмножеств маршрутов можно рассматривать как узлы дерева, как раз поэтому рассматриваемый метод и называют методом ветвей и границ (или он также известен как метод поиска по дереву решений).

По показанному алгоритму была разработана программа, осуществляющая решение задачи коммивояжера с помощью метода ветвей и границ, также визуализирующая конечный маршрут и осуществляющая вывод промежуточных результатов в файл. Её работа была проверена, как для небольших задач, так и для большого количества точек, а также была произведена оценка скорости, программной применимости рассматриваемого метода и сложности его реализации. Рассмотрим один из примеров.

Пусть имеется девятнадцать городов, то есть девятнадцать пар координат их местоположения на плоскости:

(55;140), (50;130), (70;120), (65;135), (70;130), (10;90), (20;90), (15;80), (30;80), (40;80), (20;70), (40;70), (100;80), (130;90), (120;90), (140;95), (80;10), (90;20), (60;20).

После внесения этих данных в нашу программу мы получили следующий рисунок:

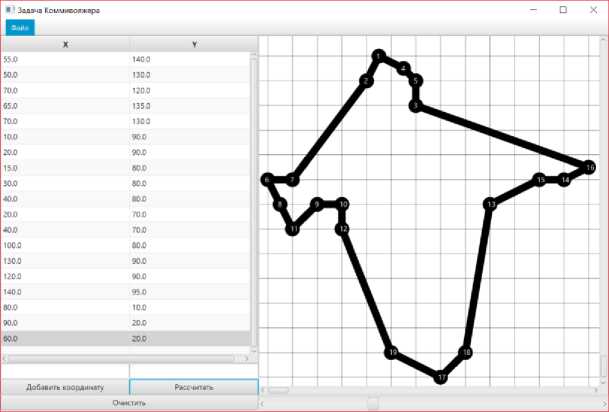
Рис. 1

Точки - это города на плоскости, числа на них - это порядковые номера городов при внесении данных в программу. В данном примере сам маршрут начинается и заканчивается в городе 18, а отсутствие пересечений путей говорит о правильности работы программы, что было проверено еще на начальных этапах её разработки с использованием генератора случайных чисел для задания координат (см. рис. 2)

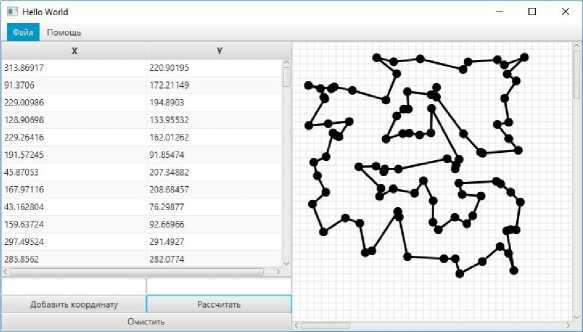
Рис. 2

Таким образом, была разработана программа, осуществляющая решение задачи коммивояжера наиболее точным, оптимальным по всем параметрам, методом, методом ветвей и границ, а также на примерах показана правильность работы изготовленного ПО, что подтверждает эффективность программы при решении поставленных задач любой сложности.