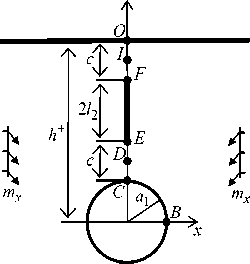
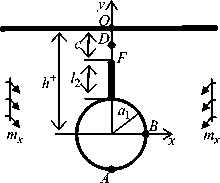
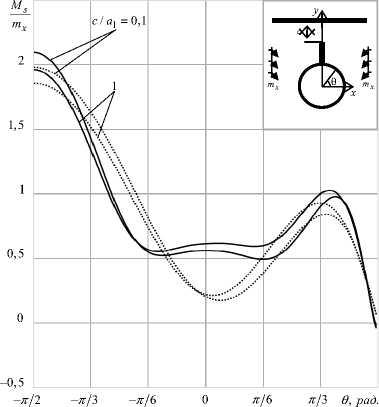
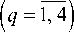Решение задачи о поперечном изгибе электромагнитоупругой полуплоскости с отверстиями и трещинами

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

Тонкие пластинки с отверстиями и трещинами из пьезоматериалов получили широкое применение в качестве элементов различных конструкций современной науки и техники [1–7]. Такие элементы часто находятся в условиях поперечного изгиба тонких плит и под действием различных механических и электромагнитных воздействий около отверстий и трещин возникают высокие концентрации изгибающих моментов (напряжений), что необходимо учитывать при проектировании и эксплуатации конструкций. Различные подходы определения электромагнитоупругого состояния (ЭМУС) пьезоплит простой геометрической формы из материалов простейшей микроструктуры были предложены в работах [8–15]. Но эти методы для определения ЭМУС пьезоплит с отверстиями и трещинами при произвольных их расположениях непригодны или неэффективны. Наиболее достоверные же результаты при определении ЭМУС многосвязных плит получаются при использовании для решения задач комплексных потенциалов теории изгиба электромагнитоупругих тонких плит [16; 17]. К настоящему времени с использованием этих функций авторами данной статьи решены различные задачи для конечных и бесконечных плит с отверстиями и трещинами.

Для случая же изгиба полуплоскости, вблизи прямолинейной границы которой располагаются кон- центраторы моментов, такая задача вообще не рассматривалась, хотя из исследований для плоской задачи теории упругости анизотропного тела известно, что именно в этом случае около отверстий и трещин возникает особенно высокая концентрация напряжений. При этом известно, что в случае многосвязной полуплоскости наиболее достоверные результаты получаются при удовлетворении граничным условиям на прямолинейной границе методом интегралов типа Коши. Этот подход для решения задач теории упругости в случае анизотропной полуплоскости был предложен в работе [18], а затем с его использованием были решены разнообразные задачи, включая сложные задачи о действии в многосвязной полуплоскости сосредоточенных сил. В работе [19] сфера действия метода интегралов типа Коши была расширена за счет его использования при определении общего вида комплексных потенциалов в задаче для многосвязной анизотропной полосы с отверстиями и трещинами, когда для определения неизвестных коэффициентов рядов Лорана использовалcя обобщенный метод наименьших квадратов (ОМНК) [20].

В данной работе с использованием комплексных потенциалов теории изгиба тонких электромагнитоупругих плит впервые построены решения задач об изгибе полуплоскости с внутренними отверстиями и трещинами. При удовлетворении граничным условиям на прямолинейной границе использован метод интегралов типа Коши, позволивший построить общий вид комплексных потенциалов, точно удовлетворяющих граничным условиям на прямолинейной границе. Для удовлетворения граничным условиям на контурах отверстий и трещин используется ОМНК. Описаны результаты численных исследований ЭМУС по изгибу полуплоскости с круговым отверстием или трещиной, с круговым отверстием и трещиной в перемычке, в том числе выходящей из контура отверстия. Исследованиями изучены закономерности изменения ЭМУС рассматриваемых плит в зависимости от их материалов и геометрических характеристик отверстий и трещин.

Постановка и решение задачи

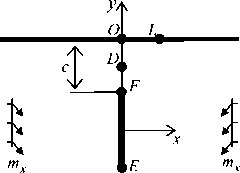
Пусть пьезоплита занимает многосвязную нижнюю полуплоскость S - с прямолинейной границей L и эллиптическими отверстиями с контурами L l ( l = 1, ^ ) (рис. 1). Выберем систему координат Oxy с началом в произвольной точке полуплоскости на расстоянии h⁺ от прямолинейной границы L⁺ и осью Ox, параллельной этой границе.

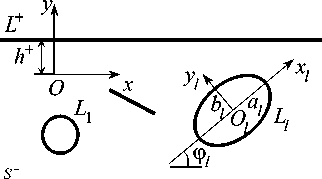
Рис. 1. Схема расчетной области

Fig. 1. Scheme of the computational domain

Обозначим полуоси эллипса Ll через al , bl , угол между полуосью al и осью Ox , отсчитываемый от положительного направления оси Ox против часовой стрелки, – через φl . При этом некоторые из эллипсов могут быть прямолинейными разрезами; при наличии отверстий с криволинейными контурами последние можно аппроксимировать совокупностями дуг эллипсов и берегов разрезов. Выберем локальные системы координат Olxlyl с началами в центрах эллипсов Ll и осями Olxl вдоль полуосей al , отсчитываемых от положительного направления Ox против часовой стрелки. Тогда в системе Oxy уравнения Ll записываются в виде x = xоi + xi cos фi - У1 sin фi, y = yоi + Xi sin фi + yi cos фi,              (1)

где xi = ai cos 0, yi = bi sin 0 ;

x _{0 l} , y _{0 l} – координаты начала локальной системы O_lx_ly_l в основной системе Oxy ; 0 - параметр параметрического задания эллипса, изменяющийся от 0 до 2 п . Прямолинейная граница L не загружена и не подкреплена. На контурах отверстий L, ( I = 1, ^ ) действуют механические изгибающие моменты m_l ( t ), поперечные силы p_l ( t ), моменты электрической индукции m_dl ( t ) и магнитной индукции m_bl ( t ) или они жестко подкреплены. На бесконечности полуплоскость не загружена или действуют механические моменты M x и моменты индукций M dx , M bx , остальные моменты равны нулю, т. е.

M y = H y = M = M = 0.

Если задачу по определению ЭМУС рассматриваемой полуплоскости решать с использованием комплексных потенциалов электромагнитоупругости [16; 17], то она сводится к нахождению из соответствующих граничных условий функций Wk(zk) (k = 1,4) обобщенных комплексных переменных zk = x + ИкУ , (2)

где μ _k – корни известного характеристического уравнения 8-го порядка, из граничных условий на контурах L_l

2Re E g ik W k ( t k ) = f_a ( t ) ,             (3)

к = 1

в котором

^{( g} 1 ki ’ ^g 2 ki ’ ^g 3 ki ’ ^g 4 ki ) = ( p k / ^R к ’ q k ’ d yk ’ ^byk ) ,

s

( fii ⁽ t )> ^f 2 i ⁽ t )> ^f 3 1 ⁽ t )> ^f 4 1 ⁽ t ) ) = I f ( m i dy ⁺ fldx ) ^- c i x ⁺ c 1 i ’

\ о sss f (mdx- f dy) + ciy + c2i, - f mdds + c3i,-f mud + c4i I;

0                                      0                  0                J

s fl(s) = f Pl(s)ds’ если на контуре Ll заданы механические изгибающие моменты Mn = m, (s) и поперечные усилия Nn = pi (s), изгибающие индукционные моменты Mdn = mdi (s), Mbn = mbl (s)’ и

⁽ g 1 ki ’ g 2 ki ’ g 3 ki ’ g 4 ki ) ( 1’ R k ’ ^d yk ’ ^byk ) ’

( fli (t)’ f 2i (t)’ f,i (t)’ f 4i (t) ) = c3l,c4l,

s

^- f m di ds + c 5 i ’

s

^- f m bi ds ⁺ c 6 i

когда контур L_l плиты жестко подкреплен; p_k , q_k , d_yk , b_yk – известные постоянные [16, 17], c_l – вещественные, c_il – комплексные постоянные.

В рассматриваемом случае комплексные потенциалы имеют вид

с

W k ( z_k ) = Г _kz_k + W ko ( z_k ) + £ W ‘ ( z_k ) ,       (4)

i = 1

g 1 kl    g 1 k        - ^g 2 kl    ^g 2 k    q k - ^g 3 kl   ^g 3 k   ^dyk -

μk g 4 kl = g4 k = byk -

( f ⁺ ( t )- f 2 ⁺ ( t )- f 3 ⁺ ( t )- f 4 ⁺ ( t ) ) = ( 0- 0- 0- 0 ) .

где Г _k - постоянные, определяемые из решения системы линейных алгебраических уравнений 8-го порядка

Г                                1 1

2Re E l P k ^- q k ^- r k - d xk ^- d yk ^- b xk ^- b yk — | Г k = k = 1 1                               H k J             (5)

( - M -0-0- - M dx -0, - M ^ -0,0 ) ;

Тогда граничные условия на прямолинейной границе запишем в виде системы gk Wk(tk ) + gIk +Wk+1 (tk +1) + gIk+2 Wk+2 (tk+2 ) +

+gu .w. (tk+3)=-E g + Wk+q-1( tk+q-1) - q=1

rk - dxk - bxk - известные постоянные [16- 17]; W'k0 (zk) -функции- голоморфные в нижних полуплоскостях Sk- -получаемых из заданной области S- аффинными преобразованиями (2); W‘ (zk) - функции- голоморфные вне контуров Lu областей Sk - соответствующих эллипсам Ll области S- при аффинных преобразованиях (2) и после конформных отображений zk = zkl + Rkl l Zkl + V I -                  (6)

k       ^Z kl J

g 20 k W k (t k ) + g 20 k + W k + 1 ( t k + 1 ) + g 20 k + 2 W- ( t k + 2 ) +

+ g0k W (tk+3 ) = -E g +   Wk+ q-1(tk+q-1) - q =1

g 0 k W k ( t k ) + g 0 к + W + 1 ( t k + 1 ) + g 30 k + 2 W k + 2 ( t k + 2 ) +

+ g0k+3Wk+3(tk+3) = -E g      Wk+ q-1(tk+q-1) - q=1

g 4 k W k ( t k ) + g 4 k + W k + 1 ( t k + 1 ) + g 4 k + 2 W k + 2 ( t k + 2 ) +

+ g 0 k + 3 W k + 3 ( t k + 3 ) = - E g 4 k + q - 1 W k + q - 1 ( t k + q - 1 )      (8)

q = 1

с определителем

в которых

Д

zkl = ^X 0 1 ^{+ H} k У 0 1 -

g ₁ ⁰ _k g ₂ ⁰ _k g ₃ ⁰ _k g ₄ ⁰ _k

^g 1 k + 1 ^{0 g} 2 k + 1

^g 3 k + 1

^g 4 k + 1

^g 1 k + 2 ^{0 g} 2 k + 2

^g 3 k + 2

^g 4 k + 2

^g 1 k + 3 ^{0 g} 2 k + 3

^g 3 k + 3

^g 4 k + 3

E g M i =1

a l ( cos ф I ⁺ p k sin Ф I )^{+ ib}i ( sin Ф I - H k cos Ф I ) Rkl =----------------------~----------------------

mkl

a l ( cos ф l + p _k sin ф l ) - ib l ( sin ф l - p _k cos ф l ) 2 R kl

x _{0 l} , y _{0 l} – координаты центра эллипса L_l в основной системе координат Oxy , эти функции можно разложить в ряды Лорана вида

в котором M_i – алгебраические дополнения элементов первого столбца g_i ⁰ . При этом – индекс, принимающий значения 1 - 4 - причем значения индекса k + q - 1 -большие 4- формально полагаются равными k + q - 5 .

Решая систему (8), найдем

W k ( t k ) ~

^Д k

W k ( z k ) = E ^akln ф kln ⁽ z k );                 ⁽⁷⁾

n = 1

^ф kln ⁽ z k ) =

Z kl ( Z k )

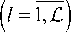
a_kln – неизвестные коэффициенты.

Для прямолинейной границы L ⁺ в граничных условиях имеем (для этого случая коэффициенты перед комплексными потенциалами обозначим индексом нуль вверху)

где	4
	0 ^E g 1 k + q - 1 q = 1 4	w' W k + q - 1	( tk + q - 1 )	g 1 k + 1	g 1 k + 2	g 1 k + 3
Д 1 k =	0 ^E g 2 k + q - q = 1 4	W k + q - 1	( t k + q - 1 )	g 2 k + 1	g 2 k + 2	g 2 k + 3
	0 ^E g 3 k + q - q = 1 4	W k + q - 1	( t k + q - 1 )	g 3 k + 1	g 3 k + 2	g 3 k + 3
	0 / >  g 4 k + q - q = 1	w' W k + q - 1	( t k + q - 1 )	g 4 k + 1	g 4 k + 2	g 4 k + 3

или

M ⁴⁴

W k⁽. tk ) =- -Ti- EE g ik + q - 1 W k + q - 1⁽ t k + q —0 .

A k i = 1 q = 1

Заменяя в этих соотношениях граничные значения t_k переменными z_k областей S_k , приходим к конформным отображениям

Окончательно граничные условия на прямолинейной границе запишем в виде

W k ( t k ) = — E r + q - 1 Wi q - 1 ( t k + q - 1 ) ( ^{k =} 1,4 ) ,     (9)

q = 1

^Zk =- (R k + q - 1 ^- ц k ) ^{h ++ Z}k + q - 1 1 ⁺

где

E ^{4 g}ik + q -1 , ,

M_i i = 1 ^A k

Для точек прямолинейной границы L+ имеем x = t, y = h+, z = x + iy = t + ih +, = tk + (цk+q-1 -pk)h+

z k = tk = ^{x +} ц k y = t ⁺ ц k h ⁺ ,

tk = t+ цkh + = t+ цkh+ + (цk -цk)h + = tk + (цk -цk)h +,

( k + q - 1 = ( ⁺ ц k + q - 1 ^h = ( ⁺ ц k^{h +} (ц k + q - 1 - И k ) ^h =

= t k ^{+ (} ц k + q - 1 - ц k ) ^{h +} , ( q = 1, ⁴ ) .

где переменная Z для лучшего восприятия заменена на Z⁺ , что подчеркивает ее происхождение от условий на границе L ⁺ .

Равенства (12) представляют собой конформные отображения внешностей единичных кругов |Z +_{+ q} - 1 l | >  1 на внешности контуров L +_{+ q} - 1 l верхней (относительно границы L ) полуплоскости S k переменной z_k . Следовательно, функции W k + q - 1 l ( z_k ) являются функциями, голоморфными вне контуров L +_{+ q} - 1 l верхних полуплоскостей S k (а следовательно, они голоморфны в нижних по-

Подставив функции (4) в граничные условия (9) на прямолинейной границе L⁺ , получим

луплоскостях S_k ^- ), и для них имеют место разложения в ряды Лорана вида

E r k + q - 1 q = 1

r

W‘0 (tk) + E Wki (Zk ) = l=1

r _______

WL q - 1,0 ( 4 + q - 1 ) + E ^Wi q - 1 1

l = 1

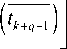
где

к

^Wk + q - 1 1 ^{( Z}k ) = E a k + q - 1 ln ^ф k + q - 1 In ^{( Z}k ) ’         ⁽¹³⁾

n = 1

^ф k + q - 1 In ^{( Z}k ) =

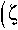
+ ⁿ k + q - 1 1 )

Здесь учтено, что на основе системы уравнений (5)

Гkt - E rk+q-1 Гk+q-1 tk+q-1 = 0 ■ q=1

На прямолинейной границе для граничных значений сопряженных величин имеем

W k + q - 1,o ( t k + q - 1 ) = W k + q - 1,o ( t k + q - 1 ) = W k + q - 1,0 ( t k + (ц k + q - 1 - ц k ) h⁺

^Wk + q - 1 1 ⁽ t k + q - 1 )    ^Wk + q - 1 1 ( t k ^{+ (ц} k + q - 1    И k ) ^h )

к

=    +               _______________ a^{k +} q ^{- 1} ln _______________

Wk+q-11 ( tk ) Er                _______ .-in n=1 [Zk+q-11 ( tk + (цk+q-1 - цk )h )J

Кроме того, при переходе в конформных отображениях (6) к сопряженным величинам и замене граничных значений по формулам (10) для граничных значений переменных находим

Z ++q-1 l - переменные, определяемые из конформных отображений (12).

Исходя из указанных свойств, входящих в условия (11) функций, умножив обе части этих условий на ядро

Коши          и вычислив интегралы типа Коши от

2пi t - zk них по бесконечной прямой L+ , получим

^W k0 ^{( Z}k ) = - EE r k + q - 1 ^W k + q - 1 1 ( t k ^{+ (ц} k + q - 1 - ^ц k ) ^h ) ■ l = 1 q = 1

Подставив эти функции Wk'0 (zk) в (4), для комплекс- ных потенциалов получим

Wk ( z+ ) = Г +z+ +

⁺ E ^Wki ^{( z}+ ) E r kk + q - ^Wk+ q - 1 1 ( t k ^{+ (} ц k + q - 1 - ц k ) ^{h +})

i = 1 L                  q = 1

а затем на основе разложений (7) и (13) будем иметь выражение

• k + q - 1 = t k ⁺ ( Ц k + q - 1 ^ц k ) h

W k ( Z k ) = Г +z+ +

• k + q - 1 1 ^{+ 1} k+ ₊ q - 1 1

r +         mk + q - 1 1

Z k+q-11 +

^Zk+q-11

Г к

+EE

akin^фkin^(zk ) Xrkk+q-1 ak+q-1 in Фk+q-1 in^(zk ) ,

в котором

^φkln^(zk⁾

n^{, z}kl

^{+                     1}

^фk+q-1 In⁽zk )    .          ,_n

(^Zk + q-11 )

.

Функции (14) точно удовлетворяют граничным условиям на прямолинейной границе L⁺. Но они содержат неизвестные коэффициенты рядов a_kln (k = 1,4; l = 1, C, n = 1, 2,...). Для определения этих коэффициентов используем граничные условия (3) на контурах отверстий, предварительно продифференцировав их, чтобы исключить входящие в их правые части постоянные. Имеем

2Re£giki§k,Wk(tk ) = fr-, (15) k=1 ds где 8k = ^k- = x ^ky= ; x', y' - производные пере’ ds x 2 '2 + y '2

менных (1) по параметру 0 параметрического задания эллипсов; s – длина дуги контура, обходимого против часовой стрелки;

^2Re£ ^iak„ 1 = 0 (p = 1 ^c), k=1

следующие из условия однозначности прогиба при полном обходе контуров отверстий L_p .

Систему (17), дополненную уравнениями (18), будем решать с использованием сингулярных разложений [23; 24]. После нахождения псевдорешений этой системы постоянные a_kln, а следовательно, и функции Wk(z_k), будут известными. После определения этих функций из граничных условий на контурах пластинки комплексные потенциалы будут известными, и по ним можно вычислять основные характеристики ЭМУС (моменты механические изгибающие, крутящий, индукций и перерезывающие силы на основных площадках). В частности, для механических моментов и моментов индукций (векторов индукций) имеют место формулы

(Mx, My,Hxy ) = -2Re£(pk, qk, Г) W‘(Zk);

k=1

( Mdx, Mdy, Mbx, Mby ) = 2Re£ ( dx_k, dyk,bxk,byk) Wk'(Zk) .

k=1

c »

W‘( Zk ) = Г k +

⁺£ £ ^фkln⁽zk ) akln   £ rkk + q-1 ^фk+q-1 In⁽zk ) ak+q-1 In

‘ (, ) =n kln k

^Zkl¹Rk, (y_u^-m_u)

'+

Ф k+q-1 In

(zk ) =

(^Zk+q-11

^Lk+q-11

n

mk+q-11

)■

Граничным условиям (15) на контурах отверстий будем удовлетворять обобщенным методом наименьших квадратов [20–22]. Для этого выберем на каждом из контуров Lp области S^-систему точек M_pm (x_pm, y_pm)

(p = 1, C, m = 1, M_p), в которых удовлетворим соответствующим граничным условиям, подставив в них функции (16). Тогда для определения неизвестных постоянных a_kln получим следующую систему линейных алгебраических уравнений:

4 C -

2Re £££ gkp 8 k, k =1 l = 1 n =1

^фН_П⁽tkpm ) akln   £ rkk + q-1 9k + q-1 ln⁽tkpm ) ak + q-1 ln

= -2Re£gikp8k,sГk (i = 1,4; p = 1, C; m = 1, Mp). (17) k=1

Кроме уравнений (17), для каждого контура отверстия должны выполняться уравнения

Зная основные характеристики, можно найти также моменты на произвольных площадках с нормалью n и касательной s, используя формулы

M„ = M, cos²nx + M,, cos²ny + 2H , cos nx cos ny , nx      y       xy

M„ = M. cos²ny + M, cos²nx - 2H , cos nx cos ny , sx       y       xy

H_ns = (M_y - Mx) cos nx cos ny + H_xy (cos²nx - cos²ny).

^Mdn = ^Mdx^{cos nx + M}dy^cosny ,

^Mbn = ^Mbx cos nx^{+ M}by cos W .

При этом если некоторый эллипс Ll переходит в прямолинейный разрез-трещину, то для его концов можно вычислить также коэффициенты интенсивности моментов (КИМ), в частности, на основе известных формул k1M =2Re £ [pk sin2 фl+ qk cos2 фl- 2rk sin фlcos фl ] Mk, k=1

±                                                           2           2

^k2M =^2Re£[(qk^-p_t)^cosфi sinфi+rk (^cosфi^-sin фi)JMk, k=1

в которых a,

Mk = + — £(± 1)nna^ .

kkln

2R_{kl n=1}

Как частные случаи, из приведенного решения задачи электромагнитоупругости (ЭМУ) следуют решения задач электроупругости (ЭУ), магнитоупругости (МУ) и теории упругости (ТУ). Эти решения получаются из

приведенного решения, если в нем принять равными нулю соответственно p^ , V jj (в задаче ЭУ), g ij, Vj (в задаче МУ) или и те и другие (в задаче ТУ). Но для проведения численных исследований во всех этих случаях можно пользоваться программой решения общей задачи электромагнитоупругости, проводя вычисления для модельного материала с постоянными

.. р g j gg j , p j pp j , j gp j , где Xg , Xp, Xgp - пьезопараметры модельного материала, gij, p jj, V j - соответствующие постоянные в уравнениях электромагнитоупругого состояния материала плиты. При этом для задач ЭМУ нужно принять X g = X p = X gp = 1, а для других задач, как следует из вычислительных экспериментов, эти параметры нужно принять такими: Xg = 1, Xp = Xgp < 10 3 для задач ЭУ; Xp = 1, Xg =Xgp < 10^3 для задач МУ; Xp = Xg = Xgp < 10-3 для задач ТУ.

Описание результатов численных исследований

Были проведены исследования для плит из материалов: 1) композит на основе BaTiO3-CoFe2O4 (материал М1) [25; 26]; 2) композит, упругие, пьезоэлектрические и электрические постоянные которого соответствуют селениду кадмия CdSe , а пьезомагнитные и магнитные – BaTiO3 (материал М2) [27]; 3) композит, упругие, пьезоэлектрические и электрические постоянные которого соответствуют PZT-4 , а пьезомагнитные и магнитные – CoFe2O4 (материал М3) [27].

При проведении исследований количество членов в бесконечных рядах (16) для каждого отверстия L_p и «коллокационных точек» M_p на этом контуре, для которых составлялись уравнения (17), увеличивалось до тех пор, пока граничные условия на контурах не удовлетворялись с достаточно высокой степенью точности (модуль абсолютной погрешности не превышал 10-3). В описываемых ниже случаях для такого удовлетворения граничным условиям необходимо было в указанных рядах оставлять от 10 до 150 членов, и на каждом из контуров брать от 100 до 500 «коллокационных точек».

В табл. 1 для задач ЭМУ и ТУ изгиба моментами MX = mx полуплоскости из различных материалов с круговым отверстием радиуса a₁ (рис. 2) с точностью до множителя m_x приведены значения изгибающих моментов в некоторых характерных точках полуплоскости в зависимости от отношения c/ a₁ , где c – длина перемычки между контуром отверстия и границей полуплоскости. При этом характерными были точки A (0, -a₁),

B (a₁,0), C (0, a₁) D (0, a₁+ с/2), O (0, a₁+ c), L (a₁, a₁+ с). Здесь и далее для полуплоскости из М1, близкого по упругим свойствам к изотропному материалу, значения величин в задачах ЭМУ и ТУ в указанных точках совпадают, отличаясь друг от друга лишь в точке В менее чем на 2 %, данные приведены лишь для задачи ЭМУ. На рис. 3 для полуплоскости из наиболее пьезоактивного материала М2 для некоторых значений с /a₁ изображены графики распределения M_s /m_x по контуру отверстия в зависимости от центрального угла 0, отсчитываемого от оси Ox против часовой стрелки, причем сплошные линии относятся к задаче ЭМУ, пунктирные – к задаче ТУ. На рис. 4 представлены графики распределения M_x / m_x вдоль границы полуплоскости из материалов М2 и М3.

Рис. 2. Схема полуплоскости с круговым отверстием

• Fig. 2.    Scheme of a half-plane with a circular hole

Как следует из табл. 1, рис. 3 и рис. 4, с приближением отверстия к прямолинейной границе значения моментов в точках перемычки резко возрастают, незначительно изменяясь в остальных точках. Концентрация моментов наблюдается и вблизи точки перемычки на прямолинейной границе, причем при удалении от этой точки значения моментов резко уменьшаются, а затем растут до значения, соответствующего случаю полуплоскости без отверстия (M_x / m_x = 1). Эта закономерность отличает изгиб полуплоскости от растяжения (плоская задача) [18; 19], когда при уменьшении длины перемычки значения напряжений в точке перемычки на прямолинейной границе уменьшаются, затем при удалении от этой точки наблюдается их увеличение, и лишь затем их снижение до значений в сплошной полуплоскости. На значения изгибающих моментов интенсивно влияет учет пьезосвойств материала (ср. значения моментов в задачах ЭМУ и ТУ), особенно в зоне перемычки между отверстием и прямолинейной границей. В точках высокой концентрации напряжений значения моментов в задачах ЭМУ и ТУ отличаются друг от друга около 15 %. Поэтому при исследованиях концентрации напряжений (следовательно, и моментов) в элементах конструкций из пьезоматериалов нельзя ограничиваться решением задачи ТУ, а нужно решать задачу ЭМУ.

Таблица 1

Значения изгибающих моментов в некоторых точках полуплоскости с круговым отверстием в зависимости от с/а1

Table 1

The values of bending moments at some points of the half-plane with a circular hole, depending on с/а1

Материал	Точка	Момент	Задача	с/а1
				∞	2	1	0,5	0,1	0,01
М1	A	Mx	ЭМУ	1,813	1,854	1,894	1,946	2,061	2,152
	B	My	ЭМУ	0,231	0,228	0,224	0,216	0,193	0,175
			ТУ	0,227	0,224	0,219	0,211	0,189	0,172
	C	Mx	ЭМУ	1,813	1,898	2,059	2,408	4,388	12,83
	D	Mx	ЭМУ	1,000	1,335	1,662	2,150	4,287	12,80
	O	Mx	ЭМУ	1,000	1,230	1,536	2,044	4,240	12,79
	L	Mx	ЭМУ	1,000	1,154	1,218	1,180	0,777	0,326
М2	A	Mx	ЭМУ	1,811	1,847	1,886	1,938	2,054	2,144
			ТУ	1,713	1,753	1,791	1,838	1,939	2,016
	B	My	ЭМУ	0,609	0,600	0,589	0,567	0,506	0,458
			ТУ	0,220	0,217	0,212	0,205	0,184	0,169
	C	Mx	ЭМУ	1,811	1,876	2,023	2,378	4,356	12,66
			ТУ	1,713	1,800	1,964	2,310	4,180	12,01
	D	Mx	ЭМУ	1,000	1,328	1,657	2,151	4,266	12,63
			ТУ	1,000	1,341	1,654	2,113	4,105	11,99
	O	Mx	ЭМУ	1,000	1,322	1,625	2,105	4,244	12,62
			ТУ	1,000	1,246	1,553	2,036	4,073	11,98
	L	Mx	ЭМУ	1,000	1,133	1,160	1,097	0,682	0,249
			ТУ	1,000	1,147	1,184	1,122	0,714	0,299
М3	A	Mx	ЭМУ	1,464	1,503	1,533	1,566	1,628	1,672
			ТУ	1,421	1,458	1,487	1,518	1,575	1,614
	B	My	ЭМУ	0,125	0,122	0,121	0,121	0,120	0,119
			ТУ	-0,070	-0,069	-0,068	-0,067	-0,064	-0,062
	C	Mx	ЭМУ	1,464	1,576	1,749	2,062	3,587	9,809
			ТУ	1,421	1,526	1,699	2,012	3,490	9,473
	D	Mx	ЭМУ	1,000	1,331	1,585	1,961	3,552	9,800
			ТУ	1,000	1,343	1,592	1,948	3,468	9,467
	O	Mx	ЭМУ	1,000	1,344	1,612	1,977	3,555	9,800
			ТУ	1,000	1,290	1,556	1,925	3,459	9,465
	L	Mx	ЭМУ	1,000	1,088	1,035	0,907	0,498	0,173
			ТУ	1,000	1,094	1,053	0,932	0,541	0,234

Рис. 3. Графики распределения моментов M_s /m_x около контура кругового отверстия в полуплоскости из М2. Сплошные линии относятся к задаче ЭМУ, пунктирные – к задаче ТУ

• Fig. 3.    Graphs of the distribution of moments M_s /m_x near the contour of a circular hole in a half-plane of material M2.

Рис. 4. Графики распределения M_x /m_x по отрезку прямолинейной границы в полуплоскости с круговым отверстием для некоторых значений с / a₁. Сплошные линии относятся к полуплоскости из материала М2, штриховые – к полуплоскости из материала М3

• Fig. 4.    Graphs of the distribution of M_x /m_x along a straight-line boundary segment in a half-plane with a circular hole for some values of с /a₁. Solid lines refer to a half-plane made of M2 material, the dashed lines refer to a half-plane made of M3 material

В табл. 2 для изгиба моментами MX = mx полуплоскости с вертикальной трещиной полудлины l1 (рис. 5) с точностью до множителя mx приведены значения КИМ k1 (КИМ k2 = 0) для концов E (0, -11), F (0,11) трещины и изгибающих моментов Mx в некоторых характерных точках полуплоскости в зависимости от отношения c/ l1 , где c – длина перемычки между трещиной и границей полуплоскости. При этом характерными точками были D (0, 11 + с/2), O (0, 11 + c), L (11, 11 + c) . Как следует из данных этой таблицы, при приближении трещины к границе полуплоскости значения изгибающих моментов в точках перемычки резко растут; вдоль прямолинейной границы уже при небольшом удалении от перемычки влияние трещины на значения моментов мало, и при x /11 > 1 этого влияния почти нет; значение КИМ для ближайшей к границе полуплоскости вершины F резко растет, тогда как для дальней вершины E оно изменяется незначительно. Как и в предыдущем случае, на значения моментов существенно влияет учет пьезосвойств материала, особенно в точке перемычки вблизи прямолинейной границы, где для близких расстояний между трещиной и границей полуплоскости значения изгибающих моментов в задаче ЭМУ на 20 % больше, чем в соответствующей задаче ТУ; в отличие от изгибающих моментов, на значения КИМ учет пьезосвойств влияет незначительно.

Рис. 5. Схема полуплоскости с трещиной

Fig. 5. Scheme of a half-plane with a crack

Таблица 2

Значения КИМ k₁ и моментов M_x /m_x в некоторых точках полуплоскости с вертикальной трещиной в зависимости от c/ l₁

The values of stress intensity factor k₁ and moments M_x / m_x at some points of the half-plane with a vertical crack, depending on c/ l₁

Table 2

Материал	Точка	Величина	Задача	c/ l1
				X	2	1	0,5	0,1	0,01
М1	E	к-	ЭМУ	1,000	1,013	1,029	1,054	1,126	1,211
	F	К	ЭМУ	1,000	1,018	1,050	1,117	1,502	3,027
	D	Mx	ЭМУ	1,000	1,191	1,451	1,964	5,476	34,60
	O	Mx	ЭМУ	1,000	1,117	1,306	1,708	4,607	28,97
	L	Mx	ЭМУ	1,000	1,071	1,076	1,006	0,837	0,726
М2	E	к:	ЭМУ	1,000	1,010	1,023	1,043	1,106	1,185
			ТУ	1,000	1,013	1,029	1,053	1,124	1,209
	F	к+	ЭМУ	1,000	1,014	1,040	1,095	1,444	2,906
			ТУ	1,000	1,018	1,049	1,115	1,498	3,020
	D	Mx	ЭМУ	1,000	1,187	1,443	1,953	5,497	35,11
			ТУ	1,000	1,191	1,451	1,964	5,479	34,64
	O	Mx	ЭМУ	1,000	1,154	1,400	1,916	5,550	35,66
			ТУ	1,000	1,119	1,311	1,719	4,657	29,33
	L	Mx	ЭМУ	1,000	1,045	1,053	1,009	0,869	0,775
			ТУ	1,000	1,060	1,046	0,975	0,834	0,744
М3	E	К	ЭМУ	1,000	1,010	1,024	1,044	1,108	1,188
			ТУ	1,000	1,012	1,028	1,052	1,122	1,206
	F	к+	ЭМУ	1,000	1,015	1,041	1,098	1,451	2,921
			ТУ	1,000	1,017	1,048	1,112	1,492	3,006
	D	Mx	ЭМУ	1,000	1,188	1,444	1,955	5,497	35,07
			ТУ	1,000	1,190	1,450	1,963	5,484	34,72
	O	Mx	ЭМУ	1,000	1,149	1,387	1,889	5,428	34,81
			ТУ	1,000	1,123	1,320	1,740	4,749	29,99
	L	Mx	ЭМУ	1,000	1,004	0,972	0,940	0,889	0,853
			ТУ	1,000	1,013	0,974	0,934	0,881	0,845

Таблица 3

Значения КИМ k₁ и моментов M_x / m_x в некоторых точках полуплоскости из М2 с круговым отверстием и центральной трещиной длины 2l₂ в перемычке в зависимости от 2l₂/a₁

Table 3

The values of stress intensity factor k₁ and moments M_x /m_x at some points of the half-plane made of M2 material with a circular hole and a central crack of length 2l₂ in the jumper, depending on 2l₂/a₁

Точка	Величина	Задача	2l2/a1
			0,1	0,3	0,5	0,7	0,9
E	К	ЭМУ	0,372	0,668	0,919	1,231	1,963
		ТУ	0,372	0,670	0,927	1,255	2,036
F	k	ЭМУ	0,369	0,648	0,877	1,160	1,863
		ТУ	0,368	0,648	0,881	1,178	1,916
B	My	ЭМУ	0,588	0,587	0,585	0,580	0,569
		ТУ	0,212	0,212	0,211	0,210	0,206
C	Mx	ЭМУ	2,047	2,251	2,784	4,172	10,93
		ТУ	1,982	2,142	2,562	3,666	9,129
D	Mx	ЭМУ	1,837	2,115	2,703	4,100	10,69
		ТУ	1,825	2,101	2,688	4,082	10,63
I	Mx	ЭМУ	1,644	1,879	2,415	3,721	10,05
		ТУ	1,613	1,847	2,382	3,684	9,893
O	Mx	ЭМУ	1,648	1,845	2,358	3,683	10,15
		ТУ	1,571	1,726	2,132	3,188	8,401

В табл. 3 для изгиба моментами MX = m_x полуплоскости из материала М2 с круговым отверстием радиуса a₁ с центром на расстоянии диаметра от границы (h⁺ = 2 a1) и вертикальной центральной трещиной переменной длины 21₂ (с центром в точке (0, a1 + a1/2)) (рис. 6) с точностью до множителя m_x приведены значения КИМ для вершин трещины (в точках E (0, a1 + c), F (0, a1 + c + 21₂)) и изгибающих моментов M_x I m_x в некоторых характерных точках полуплоскости в зависимости от отношения 2l₂/a₁. При этом длины перемычек между трещиной и другими границами с = (a1 — 21₂) 12 , а характерными точками были B(a₁,0), C(0, a₁) D (0, a1 + с/2), I (0, 2a1 — с/2), O (0, 2a1). Как следует из данных табл. 3, в случае трещины в перемычке полуплоскости с круговым отверстием с увеличением длины трещины значения изгибающих моментов около контура отверстия, в точках перемычки и прямолинейной границы вблизи перемычки резко возрастают. Как и в предыдущем случае, сильное влияние на значения изгибающих моментов оказывает учет пьезосвойств материала плиты, особенно в точке перемычки на прямолинейной границе. С увеличением длины трещины также растут значения КИМ для обоих её концов.

В табл. 4 для изгиба моментами MX = mx полуплоскости из материала М2 с круговым отверстием радиуса a1 и вертикальной краевой трещиной из контура отверстия длины 12 = a1 (рис. 7) с точностью до множителя mx в зависимости от c/ a1 , где c – длина перемычки между вершиной трещины и границей полуплоскости, приведены значения КИМ для вершины F(0, 2a1) трещины и изгибающих моментов Mx / mx в некоторых характерных точках полуплоскости. При этом характерными точками были A (0, — a1), B (a1, 0), D (0, 2a1 + с/2), O (0, 2a1 + c).

Рис. 6. Схема полуплоскости с круговым отверстием и внутренней трещиной в перемычке

Fig. 6. Scheme of a half-plane with a circular hole and an internal crack in the jumper

На рис. 8 для некоторых значений с /a₁ изображены графики распределения моментов M_s / m_x по контуру отверстия для полуплоскости из материала М2. Как следует из данных табл. 4 и рис. 8, приближение кругового отверстия с краевой трещиной к границе полуплоскости ведет к весьма существенному росту концентрации изгибающих моментов в точках перемычки, около контура отверстия и около прямолинейной границы вблизи перемычки.

Таблица 4

Значения КИМ k₁ для конца трещины и моментов M_x / m_x в некоторых точках полуплоскости из М2 с круговым отверстием и краевой трещиной в зависимости от c/ a₁

Table 4

The values of the stress intensity factor k₁ for the end of the crack and the moments M_x / m_x at some points of the half-plane made of M2 material with a circular hole and an edge crack, depending on c/ a₁

Точка	Величина	Задача	c/ a1
			0,9	0,7	0,5	0,3	0,1
F	k1+	ЭМУ	1,422	1,474	1,562	1,742	2,354
		ТУ	1,469	1,523	1,614	1,798	2,429
A	Mx	ЭМУ	1,969	1,984	2,005	2,036	2,097
		ТУ	1,864	1,877	1,896	1,924	1,979
B	My	ЭМУ	0,611	0,605	0,596	0,583	0,562
		ТУ	0,220	0,218	0,215	0,211	0,204
D	Mx	ЭМУ	1,993	2,283	2,789	3,915	9,004
		ТУ	1,975	2,259	2,754	3,859	8,844
O	Mx	ЭМУ	2,007	2,299	2,809	3,948	9,122
		ТУ	1,736	1,969	2,379	3,301	7,502

Рис. 7. Схема полуплоскости с круговым отверстием и краевой трещиной из него в перемычке

Fig. 7. Scheme of a half-plane with a circular hole and an edge crack from it in the jumper

Рис. 8. Графики распределения моментов M_s / m_x около контура кругового отверстия c краевой трещиной в полуплоскости из материала М2 для некоторых значений отношения с / a₁. Сплошные линии относятся к задаче ЭМУ, штриховые – к задаче ТУ

Fig. 8. Graphs of the distribution of moments M_s /m_x near the contour of a circular hole with an edge crack in a half-plane made of M2 material for some values of the ratio с / a₁. Solid lines refer to the electro-magneto-elasticity problem, dashed lines to the theory of elasticity problem

Заключение

Таким образом, дано решение задачи об изгибе тонкой многосвязной полуплоскости из пьезоматериала с отверстиями и трещинами. Для решения задачи использованы комплексные потенциалы электромагнитоупругости теории изгиба тонких плит [16], их разложение в ряды Лорана, удовлетворение граничным условиям на прямолинейной границе методом интегралов типа Коши [18], на контурах отверстий и трещин обобщенным методом наименьших квадратов [20–22]. При