Решение задачи о прогреве трещиноватого пласта

Как показала практика, добыча высоковязких нефтей и природных битумов неэффективна без теплового воздействия на пласт. Многочисленными теоретическими, лабораторными и промысловыми исследованиями установлено, что искусственным созданием заданных термодинамических условий в пласте можно существенно повлиять на подвижность нефти. Поэтому основной целью термических методов воздействия является нагрев пласта и содержащихся в нем флюидов.

Рассмотрим трещиноватый пласт, рассеченный системой параллельных трещин, насыщенного нефтью аномально высокой вязкости или битумом (рисунок).

Рассматривается задача о прогреве блоков пласта, рассеченного системой параллельных трещин (рисунок). Расстояния между трещинами L метров. Прогрев осуществляется теплопроводностью (коэффициент температуропроводности a ² ), конвекцией (скорость фильтрации V ). Между пластом и окружающими породами происходит теплообмен (коэффициент теплоотдачи а ). В трещинах поддерживается

температура T_П . Начальная температура пласта T ₀ .

Уравнение теплового баланса при предположениях имеет вид

таких

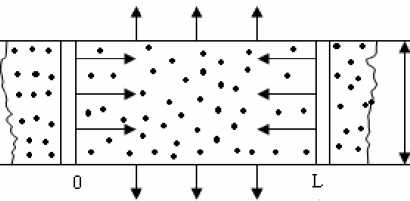
Рис. Схема трещиноватого пласта.

2 52 T     5 T а1 •—- + V--

5 x ²       5 x

—

при краевых условиях т = т ■ t=0       0 ;

^(T — T) =д т сph             о t

Т = т = т x=0     x=L     П .

В уравнении (1) с, р - соответственно теп-

лоемкость и плотность пород пласта, h – отношение площади трещины к периметру боковой поверхности.

Опыт разработки таких месторождений показывает, что при больших фильтрационных сопротивлениях пористых блоков, закачиваемый в пласт теплоноситель на начальном этапе прогрева распространяется по трещинам. После повышения температуры до определенного уровня фильтрационные сопротивления блоков уменьшаются и теплоноситель будет проникать в блоки пласта. При этом пласт начнет прогреваться не только за счет теплопроводной составляющей, но и конвекцией.

Обозначим T — T_o = AT . Откуда T = AT + T_o .

При такой замене уравнение (1) запишется в виде a2

5 ² AT     8 AT    а       8 AT

---— + V ----^^ AT =----, (3)

8x ²        8x   cph 81

при граничных условиях

ATx = o = (T — T _o )x = o = T_n — T o = AT_n

ATx=l = (T — To )x=l = Tn — To = ATn и начальном условии

AT=o = (T - To )t=0 = To - To = 0 .(5)

Будем искать решение уравнения (3) в виде

AT(x,t) = e^x+Xt • u(x,t).(6)

После подстановки (6) в уравнение (3) получим

2 52u         „ 2 . 5u a —— + (V + 2цa )+

5x                 5x(7)

+ (a ² ц ² + V ц-р-Х ) • u = —,

5 t

Уравнение (9) относительно ν(x,t) прини-

мает вид

dv    2

— = a

5 t

d2v

•^ T + X ^ AT_n

5 x ²         П

e ^-X t

(

• 1 +

A

1 - e

L

A • x

n “ где в =---~ c p h

.

Подберем ц и ражения в скобках в нуль. Это будет при

Х таким образом, чтобы вы-уравнении (7) обратились в

(15) при условиях (13) и (14).

Полученное уравнение (15) является неоднородным, но при однородных граничных условиях.

Методика решения неоднородного уравнения (15) такая же, как и для обыкновенных дифференциальных уравнений. Решение (15) будем искать в виде двух слагаемых

v(x,t) = P(x,t) + to(x,t) ,     (16)

где P(x,t) является решением задачи

ц = -

V	( V 2
—;    Х = —
2 a 2	A 4 a 2

A

+ P .

d P   ₂ d ² P

— = a-- d t         dx12

При полученных мает вид

ц

и Х уравнение (7) прини-

P( 0 ,t) = P(L,t) = 0 ,

2 d2 u a--2

d x ²

d u

d t

.

Преобразуем краевые условия (4) и (5) с помощью подстановки (6)

ux = 0 = e

'^Х t • AT_n, u_x__L x

= e ¹

ut = 0

= 0 .

■^{( ц L +X} t) • AT_n . (10)

Поставленная задача (3) трансформировалась в однородное уравнение (9) при неоднородных граничных условиях (10) и начальном условии (11).

Рассмотрим функцию u(x,t) = v(x,t) +

■ ATn • e

AT_n • e ^{- ( ц L +x} t) - AT_n • e ^-X t t । П                           Ц

L

A

• ^x ,

где u(x,t) – решение уравнения (9) при условиях (10) и (11).

Найдем значения функции ν(x,t)

x = 0 , x = Lut = 0 .

при

Pt = 0

■ ATn • 1

1 - e ^{— mL}

\

A

L

• x

e

^v t = 0

ω(x,t) – решение задачи

dm   2

— = a

5 ²ю

•

5 x²

+ X ^ AT_n

• e

^X t • 1

+

- e ^{—ц L}

A

L

^{+ 1}

-----• x ,

^m x = 0 = ^m x = L

= 0 , m_t = _o = 0 .

Решение задачи (17) хорошо известно, как решение однородного уравнения при нулевых граничных условиях [1].

Ю

^P(x,t) = j A n • exp

n = 1

L

A = - f P nt

L

( an n

^“

A

L

n п

„ • sin—xdx = -

= ⁰       L

. n n ,

• sin — xdx =

L

2 ΔT П

n П

2 ΔT П

l n • e -

L

. n к t • sin — x, где

L

^v x = 0 = ⁰ , ^v x = L

= 0 .

—

ATn • 1

1 - e ^{- M} L   A

—

A

L

• x

.

Преобразуем уравнение (9) новке (12)

согласно

подста-

L

J1

A

M L - 1 ) .

—

1 - e "^M L   A

------x

L

5 u _ d v

5 1    5 1

—

X - AT_n • e ^-X t

(

• 1 +

A

1 - e ^{- M} L

L

A • x

;

d ² u

5 x²

d ²v d x ²

P(x,t) = 2 ^ 5 ^ j r;

П n = 1

I n • e ^- ^^L

—

n

— exp

—

A

A² A an K^A t

L

n п

• sin—x - решение задачи (17).

Решение задачи (18) будем искать в виде ряда [1].

^

m(x,t)=Z Tn(t) • n =1

. ^{n п} sin x.

L

Решение (21) удовлетворяет граничным условиям to_x = ₀ = to_x = _L = 0 .

Для того, чтобы выполнялось начальное условие, необходимо

Подчиним решение (25) начальному условию (22). Получим

Т„( 0 ) = 0 .

T n (t) =

2 X • ДТ П •

I ⁿ • e "P L )

Последнее слагаемое в правой части уравнения (18) удовлетворяет условиям Дирихле и ее можно разложить в ряд Фурье по синусам

n п

f(x,t) = X ^ ДТП • e ^—X t

• 1 + 1 - e

-I

к

L

P L   J

---• x 7

exp( —X t) — exp

-

к y

( an nJ ² 1

.

L

кк

Решение задачи (18)

7 7

,

E”     \ ■ n п фn(t) • Sin —x, где n=1               L

— 1

_{z x} 2X^ Д Т_П • e

^V n (t) =---- L”

- X t L(     ,

- J 1 + ¹

— e

,^—p L

2 X • Д Т П • e

—X t

к

L

• x

. ^{n п} ,

• sin—x dx =

L

z x 2X^ ДТП m(x,t) =-----П Z п     n=1

( 1 — 2 ( — 1 ) n + ( — 1 ) n • e

,-PL )

n

( an п J

I I —X

•

n π

( 1 — 2 ( — 1 ) n + ( — 1 ) n • e

,^-p L ) .

exp( —X t) — exp

-

Последнее слагаемое уравнения (18) ставляется в виде

пред-

к

к

an n i t

L 7

кк ^L

. n л

• Sin— x.

L

2Х-ДТ -e^—X t f(x,t) = 2 ^{X Д Тп} e

Выполнив обратные подстановки, получим

•

x z n = 1

п

1 — 2 ( — 1 ) n + ( — 1 ) n • e ^

u(x,t) = ДТ П • e

ДТ_П • e - ^{( V L + X t)} — ДТ_П • e - ^{X t}

"^Xt + — ^п------------^п-- x +

L

n

. n п

• Sin — x.

L

Подставим ряд (21) в уравнение (18) и (23), получим

учтем

+ 2ДТ п Z

П n = 1

( — 1 ) n • e ^{— V L}

—

n

1 exp

( ann

—

к к L

nπ t • Sin — x +

£

x z n = 1

T „ (t) + ⁽--1 • T „ (t) к ^L 7

-

к

2 λΔT

+--- П

—

к

2 X^ ДТ П • e

n п

-^X t

- ( 1 — 2 ( — 1 ) n + ( — 1 ) n

• e

.-P L )

’ 7

x z n = 1

π

( 1 — 2 ( — 1 ) n + ( — 1 ) n e ^— " L )

• n ^П     A

• sin — x = 0 .

L

Для определения T_n(t) получим линейное дифференциальное уравнение первого порядка

n

( ann i

Г17 J к

nπ sin x.

L

— X

r exp(—Xt) — exp к

—

к

2 anπ

t

L )

dT

— + dt

an п

L

I • T n (t) =

2 X • ДТ П • e

n п

X t ,

— ( 1 — 2 ( — 1 ) n + ( — 1 ) n • e

■^{-P L} ) ,

общее решение которого

T_n(t) = C • exp

( an п J .

—

к к ^L

t +

Выполняя подстановку (6) и учитывая, что ДТ = Т — Т ₀ , получим Т = Т ₀ + e ^ x ^+X t • u(x,t) . В подробной записи решение поставленной задачи принимает вид

9 = Т - Тд

^ТП ^{— Т} 0

r

= e^ x 1

—

1 — e ^— ^L --x +

L

2 e

+ —

.Xt ” / A n

π

2 X • ДТП • +

( 1 — 2 ( — 1 ) n + ( — 1 ) n

• e ^—

PL )

n п

( an пJ    „

I I —X

• e

—X t

— I

.

x e

- z1- n=1

2 an n i ---------I t

L 7

к

• e ^— V L — 1

---------x

n

nπ sin — x + L

кк L

2 λe

+---

π

, At ^

- z n=1

(1 - 2 ( - 1 ) n + ( - We ^— " ) _x

„ ,_'2

X

n

V

— A t

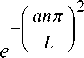
nπ sin x

L

Рассмотрим частные случаи:

1. V = 0 ^

" = 0

A = — в

прогрев теплопровод-

ностью, но учитываются потери тепла в окружаю-

щие породы. Из (28) получаем

9 to o=1+2z n n=1

n

V

—

( — 1 ) ⁿ — 1

exp

^ )

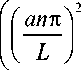
^— P t

7 7

• n П .

Sin— x +

L

+2'Z

П n = 1

n

1 — ( — 1 ) n

^

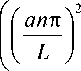
^{+ в}

1 — exp

I an n )

— I ~ 7

X ^      ^

^))

^—p t

7 77

Выводы

• 1.    Для одномерного случая (температура по толщине пласта считается постоянной) при граничных условиях 1-го рода получено решение уравнения, описывающего температурное поле нефтяного пласта при термовоздействии через трещины с учетом факторов теплопроводности, конвекции и потерь тепла в окружающие пласт породы.

• 2.    В качестве частных случаев получены зависимости для вычисления температуры только при прогреве теплопроводностью с учетом и без учета потерь тепла в окружающие пласт породы.

• 3.    Полученные в работе результаты могут быть использованы при проектировании разработки месторождений высоковязкой нефти или природных битумов, пласты которых имеют вертикальные и крутопадающие параллельные трещины.