Решение задачи о растяжении упругопластической полосы, ослабленной разрезами и отверстиями

Упругопластические задачи, в силу их практической важности, уже давно изучаются механиками. Основной проблемой, которая возникает при решении таких задач, является упругопластическая граница. Условие пластичности накладывает дополнительную связь, и это, по словам Г. П. Черепанова [1], упрощает задачу, с другой стороны, возникает новый неизвестный элемент – упругопластическая граница, затрудняющая решение. В настоящее время решения упругопластических задач продолжает оставаться в центре внимания исследователей. Появляются новые аналитические подходы к их решению, совершенствуются численные методы. Проведем краткий обзор таких работ. В [2] с помощью законов сохранения решена задача о кручении упругопластического стержня, армированного упругими волокнами. Для решения задачи используются законы сохранения. В [3] рассмотрен упругопластический коробчатый брус, который изгибается поперечной силой. Предполагается, что деформации в стержне упругопластические и боковая поверхность его свободна от напряжений. Центр тяжести поперечного сечения не совпадает с точкой приложения силы. С помощью законов сохранения построено точное решение, описывающее напряженное состояние этой конструкции. Напряженное состояние вычисляется в каждой точке рассмотренной фигуры с помощью интегралов по внешним контурам поперечного сечения. В [4] исследуется упругопластическое кручение многослойного стержня. Стержень состоит из нескольких слоев. Упругие свойства слоев различны, но коэффициент пластичности у всех слоев одинаков. В статье построены законы сохранения, которые позволили вычислить компоненты тензора напряжений с помощью контурных интегралов по границе слоев. В [5] рассматривается упругопластическое кручение анизотропного трехслойного цилиндрического стержня некругового поперечного сечения. Внутренний слой стержня находится в упругопластическом состоянии, два внешних слоя полностью пластические. Предполагается пластическая анизотропия. Параметры анизотропии каждого слоя различны. В [6] определена глубина зарождения пластической области, позволяющая контролировать степень наклепа защитного покрытия детали, не допуская его переупрочнения. В [7] дано описание испытательного комплекса и методики проведения экспериментов для изучения сложного нагружения. Приведены некоторые вопросы исследования упругопластического деформирования материалов на автоматизированном комплексе СН-ЭВМ. В [8] рассмотрено решение задачи определения упругопластического состояния тяжелого пространства, ослабленного отверстием эллиптической формы. Материал среды обладает свойствами анизотропии. Решение задачи выполнялось методом малого параметра. Кручение двухслойного стержня коробчатого сечения рассмотрено в [9]. В [10] численными методами рассчитывается напряженно-деформированное состояние связующего композитных материалов. Расслоения стальных труб при сложном нагружении моделируются в [11]. Упругопластический анализ круговой трубы, вывернутой наизнанку, проведен в [12]. В [13] изучается влияние типа плоской задачи для упругопластического адгезионного слоя на значение J-интегралов. Горячая посадка упруговязкопластического диска с некруговым включением описана в [14]. В [15] описываются явления уменьшения пластичности с увеличением предела текучести поликристалла.

В предлагаемой работе используются законы сохранений дифференциальных уравнений. Это позволяет свести нахождение компонент тензора напряжений в каждой точке к контурному интегралу по границе рассматриваемой области и дает возможность построить упругопластическую границу. При этом предполагается, что граница является кусочно-гладкой.

Постановка задачи

Рассмотрим уравнения, описывающие плоскую упругую деформацию в стационарном случае. Они состоят из уравнений равновесия дох дт n дт до

—- + — = 0, — + — - = 0

д - д у д - д у

и уравнения Лапласа, которое есть следствие совместности деформаций

Д ( о - + о у ) = 0.                                       (2)

Здесь о _X , о _у , т - компоненты тензора напряжений.

Систему (1), (2), следует решить со следующими граничными условиями о - П 1 +т n 2 I L = X ( X , у ), т П 1 +о у П 2 I L = Y ( X , у ),

( о X -о у ) ² + 4 т ² = 4 k 2 .                                      (3)

Здесь n ₁, n ₂ – компоненты вектора внешней нормали к кусочногладкому внешнему контуру и контурам отверстий, ограничивающему конечную область S . Область S приведена на рис. 1. X , Y - компоненты вектора внешних сил.

Далее предполагаем, что на боковой поверхности и контурах круглых отверстий материал находится в пластическом состоянии, поэтому соотношение Мизеса включено в (3). Здес ь k – постоянная пластичности, равная пределу текучести при чистом сдвиге.

Предполагаем, что полоса растягивается усилиями оу I у=I = 2 k, о у1у=-1 = -2 k,                         (4)

а остальные границы внешнего контура и отверстий считаются свободными от напряжений.

Отсюда следует:

• -    на границах AB, DE из (3) получаем о _у = 2 k , о _X = 0, т = 0;

• -    на границах FG, IJ - о _у = - 2 k , о _X = 0, т = 0;

• -    на границах CB, GH и границах Г_i - о _у = 2 kn 2 , о _X = 2 kn 2 , т = - 2 kn 1 n ₂;

  

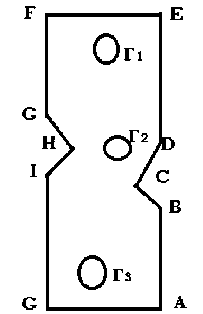
  Рис. 1. Область S

  
  

  Fig. 1. Region S

  
  
  
  

• -    на границах CD, HI о _у = - 2 kn 2 , о _X = - 2 kn 2 , т = 2 kn 1 n ₂.

Будем искать решение задач (1)–(3) в два этапа. На первом этапе решается задача Дирихле для уравнения Лапласа Дp = 0, где о - +о у = p ( x , у).

Из (3) получаем p = 2 k        на   DEFGH и Гi p = -2 k       на  HIJAB.

Для решения этой задачи используются стандартные методы. В результате в области S найдена функция p ( x , y ).

На втором этапе решаем задачу дог дт      дт дог д p „

—- + — = 0,---- + — = 0, дX   ду      дX ду   ду

со следующими граничными условиями, которые следуют из (3):

• - на границах DE, FG, IJ, AB      о x = 0, т = 0;

  - на границах CD, GH и r i         о x = 2 kn 2 , т = - 2 kn 1 n ₂;

- на границах BC, IH              о x = - 2 kn 2 , т = 2 kn 1 n ₂.

Для удобства запишем уравнения (8) в виде

F i = U x + V y = 0, F 2 =- U y + V x + f = 0,                         (10)

dp где о x = u, т = v,— = f, далее индекс внизу будет означать производную по соответствующему dУ аргументу.

Для удобства перепишем в новых терминах и граничные условия

На границах DE, FG, IJ, AB и = 0, v = 0.

На границах CD, GH и Г_i и = 2 kn 2 , v = - 2 kn 1 n ₂.                                         (11)

На границах BC, IH и = - 2 kn 2 , v = 2 kn 1 n 2 .

Решим краевую задачу (10), (11) с помощью законов сохранения.

Законы сохранения системы уравнений (10)

Определение. Законом сохранения для системы уравнений (10) назовем выражение вида

A x + B y = ^ F + И F 2 ,                            (12)

где и 1 , и ₂ - линейные дифференциальные операторы, одновременно не равные нулю тождественно,

A = а 1 и + в 1 v + Y 1 , B = а ² и + в ² v + Y ² ,                           (13)

а ¹ , в ¹ , Y ¹ , а ² , в ² , Y ² - некоторые гладкие функции, зависящие только от x , у .

Замечание. Более общее определение закона сохранения, подходящее для произвольных систем уравнений, можно найти в [16].

Из (12) c учетом (13) получаем а1 и + а1 их + в1 v + в1 vx + y\ + а2 и + а2 их + в2 v + в2 vx + Y2 = x    x x    x x y    yy    yy

= Ц( Ux + vy ) + Й2(-иу + vx + f ) = 0.(14)

Из (14) следует аX + а2 = 0, вX + в2 = 0,а1 = и ,в' = йз,а2 = -и2,в2 = ц,yx + Y2 = Иf.

Отсюда получаем а1 =в2, а2 =-Р1.(15)

Поэтому аX -РУ = 0, «y +Px = 0.(16)

Из приведённых формул следует, что система уравнений (10) допускает бесконечно много законов сохранения; далее будут приведены только те, которые позволяют решить поставленную задачу.

Поскольку сохраняющийся ток имеет вид

A = а 1 и + в ¹ v + y ¹, B = -в 1 и + а ¹ v + y ² ■

Из (16) по формуле Грина получаем

jj (Ax + By) dxdy = J - Ady + Bdx + ^ J - Ady + Bdx = 0,

S

L

i Г i

где S – область, ограниченная кривой L и контурами Г _i .

Решение задачи (10), (11)

Для нахождения значений u , v внутри области S , необходимо построить решения системы Коши – Римана (16), имеющие особенности в произвольной точке ( x ₀, y ₀) ∈ S .

Первое из таких решений имеет вид

α ¹

x - x ₀

( x - x ₀) ² + ( y - y ₀) ^{2 ,}

в ¹ =------- y-y ------2 , Y 1 = j-------y y ------2 fdx , Y 2 = 0. (18)

( x - x ₀) ² + ( y - y ₀) ²          ( x - x ₀) ² + ( y - y ₀) ²

В точке ( x ₀, y ₀) ∈ S функции α ¹ , β ¹ имеют особенности, поэтому окружим эту точку окружностью

ε :

( x - x ₀) ² + ( y - y ₀) ² =ε ² .

Тогда из формулы (17) получаем

^ J - Ady + Bdx + J - Ady + Bdx + J - Ady + Bdx = 0,

i    Г i

L

ε

Вычислим последний интеграл в формуле (19). Имеем

cf -Ady + Bdx = (J -(

u ( x - x ₀)

-

v ( y - y ₀)

ε

ε

( x - x ₀) ² + ( x - x ₀) ²    ( x - x ₀) ² + ( x - x ₀) ²

+ γ1)dy +

+

-

u ( y - y ₀)

-

v ( x - x o )

_v ( x - x ₀) 2 + ( y - y ₀) 2    ( x - x q )² + ( y - y ₀) 2 _;

dx .

Введем новые координаты x - x ₀ = ε cos ϕ , y - y ₀ = ε sin ϕ , получаем

2 π

J - Ady + Bdx = j [ - ( u cos ф + v sin p )cos ф- ( u sin ф + v cos ф ) s in ф ] d ф =

ε

2 π

- j ud ф = - 2 п u ( x ₀, y ₀).

Последнее равенство получено по теореме о среднем при ε → 0.

Для окончательного построения решения найдем значения u , v на границе L . Из (15) получаем

формул

2 no _x ( x ₀, y ₀) = j Y 1 dy + j - ( - 2 kn 2 a ¹ + 2 kn 1 n ₂ в 1 +Y 1 ) dy + (2 kn 2 в 1 + 2 kn 1 n 2 a ¹ ) dx + AB      BC

- j (2 kn 2 a ¹ - 2 kn 1 n ₂ в 1 + Y 1 ) dy + (2 kn 2 в 1 + 2 kn 1 n 2 a ¹ ) dx - j Y 1 dy - j Y dy + j Y dy + CD                                                 DE      EF      FG

+ j - (2 kn 2 a ¹ - 2 kn 1 n ₂ в 1 +Y 1 ) dy - (2 kn 2 в 1 + 2 kn 1 n 2 a ¹ ) dx +

GH

+ ∫ - ( - 2 kn ₂ ² α ¹ + 2 kn ₁ n ₂ β ¹ - γ ¹ ) dy + (2 kn ₂ ² β ¹ + 2 kn ₁ n ₂ α ¹ ) dx + ∫ γ ¹ dy - ∫ γ ¹ dy + HI                                                                     IJ        JA

+∑ ∫ (2kn22α1 - 2kn1n2β1 + γ1)dy + (2kn22β1 + 2kn1n2α1)dx.(21)

i Г i

Второе решение системы уравнений (16) возьмем в виде

α1 =      y-y0         β1 =-

( x - x ₀) ² + ( y - y ₀) ^{2 ,}          ( x - x ₀) ² + ( y - y ₀) ^{2 ,}

γ1=-∫       x2-x0      2 fdx, γ2=0.(22)

( x - x ₀) ² + ( y - y ₀) ²

Проделав выкладки, аналогичные выкладкам, проделанным с решением (18), получаем

2πτ(x0, y0) = ∫ γ1dy + ∫ -(-2kn22α1 + 2kn1n2β1 + γ1)dy + (2kn22β1 + 2kn1n2α1)dx + ABBC

- ∫ (2 kn ₂ ² α ¹ - 2 kn ₁ n ₂ β ¹ + γ ¹ ) dy + (2 kn ₂ ² β ¹ + 2 kn ₁ n ₂ α ¹ ) dx - ∫ γ ¹ dy - ∫ γ ¹ dy + ∫ γ ¹ dy CD                                                 DE      EF      FG

+ ∫ - (2 kn ₂ ² α ¹ - 2 kn ₁ n ₂ β ¹ + γ ¹ ) dy - (2 kn ₂ ² β ¹ + 2 kn ₁ n ₂ α ¹ ) dx +

GH

+ ∫ - ( - 2 kn ₂ ² α ¹ + 2 kn ₁ n ₂ β ¹ - γ ¹ ) dy + (2 kn ₂ ² β ¹ + 2 kn ₁ n ₂ α ¹ ) dx + ∫ γ ¹ dy - ∫ γ ¹ dy + HI                                                                     IJ        JA

+ ∑ ∫ (2 kn ₂ ² α ¹ - 2 kn ₁ n ₂ β ¹ + γ ¹ ) dy + (2 kn ₂ ² β ¹ + 2 kn ₁ n ₂ α ¹ ) dx .                  (23)

i Г i

Заключение

В работе предложен метод решения краевой задачи, описывающей упругопластическое напряженное состояние полосы с боковыми разрезами и отверстиями. При этом вычисления напряжения σ _x , τ сводятся только к вычислению контурных интегралов по границам области, а напряжение σ _y определяется из решения задачи (11), (12) численным решением задачи Дирихле для уравнения Лапласа. После определения всех компонент тензора напряжений необходимо найти точки области S, в которых достигается предел текучести. Это позволяет построить упругопластическую границу и тем самым оценить прочность рассматриваемой пластины. В настоящее время разрабатывается программа, позволяющая строить упругопластическую границу для растягиваемых пластин с разрезами и отверстиями.