Решение задачи о собственных колебаниях электроупругих тел с внешними электрическими цепями на основе их электрического аналога

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2018PNRPU MECHANICS BULLETIN

В работах [1, 2] была показана возможность демпфирования колебаний конструкции с присоединенным к ее поверхности пьезоэлементом с помощью внешних электрических цепей (шунтирующих цепей), присоединенных к электродированным поверхностям элементов конструкции, выполненных из пьезоэлектрических материалов. В настоящее время шунтирование внешними электрическими цепями элементов конструкций, выполненных из пьезоматериалов, для демпфирования колебаний широко применяется в технических приложениях, где малые размеры и вес объектов играют решающую роль, либо в таких условиях эксплуатации конструкции, при которых нет доступа к источникам электроэнергии. Для успешной реализации данного подхода необходимо понимание, как изменяются динамические характеристики конструкции с пьезоэлементом и внешней электрической цепью при изменении внутренних характеристик такой электромеханической системы.

При анализе динамических процессов в конструкции с пьезоэлементами и внешними электрическими цепями ее динамические характеристики могут быть определены из решения различных задач: о вынужденных колебаниях, о собственных колебаниях, о переход- ных процессах с начальными условиями. С точки зрения эффективности определения динамических характеристик и оптимизации диссипативных свойств задача о собственных колебаниях является наиболее удобной и информативной, что было продемонстрировано, например, в работах [3, 4]. В результате решения данной задачи найденные комплексные собственные значения будут определять частоты собственных колебаний и показатели демпфирования. Эффективность приложения рассматриваемой задачи для оптимизации динамических характеристик определяется их независимостью от нагрузок.

В силу особенностей математической постановки задачи о собственных колебаниях электроупругих тел с внешними электрическими цепями численная реализация алгоритма ее решения на основе метода конечных элементов является достаточно нетривиальной задачей [5], и получение решения требует существенных временных затрат из-за большой размерности разрешающей системы уравнений.

В то же время существует общность математических уравнений, которыми описываются колебания в механических системах и колебания тока и напряжения в электрических цепях. При этом индуктивность является аналогом массы, сопротивление – аналогом вязкости, а емкость – аналогом жесткости. Совпадение математических описаний позволяет рассматривать в ряде случаев вместо механической системы электрическую, применяя метод динамических аналогий, заменяя уравнения движения механической системы соответствующими уравнениями для эквивалентной электрической. Этот подход был использован, например, в работах [6–10].

Метод динамических аналогий был описан Гарри Ф. Ольсоном в [11], где приведены аналогии между элементами механических (линейных и вращающихся), акустических и электрических систем и предложено анализировать акустические и механические системы путем преобразования их к электрическим аналогам. Данный подход широко применяется для решения различных механических задач [12–20].

При этом рассматриваются два типа аналогий: при первой механические усилия заменяются электрическим напряжением, скорость – электрическим током, при второй усилия являются аналогом тока, а скорость – электрического напряжения. Второй подход имеет преимущество, состоящее в том, что структура эквивалентной электрической цепи, полученной таким образом, почти идентична структуре исходной плоской механической системы.

В настоящее время метод динамических аналогий успешно применяется при моделировании поведения конструкций с пьезоэлементами и внешними электрическими цепями (электромеханических систем).

Представление электромеханической системы в виде дискретного аналога, состоящего из элементов с сосредоточенными параметрами, позволяет существенно упростить процедуру получения ее динамических характеристик. В классической механике таким аналогом является одномассовая система типа «пружина–масса– демпфер». С помощью такого аналога можно описывать динамические характеристики исходной электромеханической системы с бесконечным числом степеней свободы в окрестности какой-либо одной резонансной частоты. С другой стороны, в электродинамике известен ряд подходов к моделированию поведения пьезоэлектриков с помощью их электрических аналогов в виде эквивалентных электрических схем [21–26]. Данные модели описывают поведение пьезоматериалов в диапазоне частот ниже ультразвука. Одна из первых моделей эквивалентной электрической цепи предложена Van Dyke [8]. Все эти модели описывают поведение пьезоэлектрика как отдельного элемента с сосредоточенными параметрами и довольно широко используются многими исследователями для понимания влияния внешней электрической цепи на исследуемую конструкцию. Однако данные модели имеют свои особенности. Модель Sherrit [22] использует комплексные элементы схемы для моделирования потерь в пьезоэлектрической керамике, поэтому компоненты цепи в модели Sherrit имеют комплексные значения, тогда как в модели Van Dyke они действительные. Модель, предложенная Guan [21], является попыткой повысить точность модели Van Dyke введением двух дополнительных сопротивлений для учета диссипации энергии на нерезонансных режимах. Mason в своей работе [27] объяснил физический смысл этих механических констант в схеме модели Van Dyke с точки зрения резонансных и антирезонансных частот.

Однако, с одной стороны, присоединение к конструкции пьезоэлемента изменяет ее механические граничные условия, с другой – на пьезоэлемент будет воздействовать конструкция, имеющая свое множество резонансов. Поэтому для моделирования поведения пьезоэлемента, прикрепленного к конструкции, необходима модель, описывающая множество резонансных частот в широком частотном диапазоне, что, соответственно, требует другой схемы электрической модели.

В настоящее время исследователями используются оба подхода моделирования исходной электромеханической системы электрическим аналогом в форме эквивалентной электрической схемы: моделирование пьезоэлемента с присоединенной к нему внешней электрической цепью без учета влияния конструкции и с учетом влияния конструкции, к которой он присоединен [8, 23, 28–30].

Влияние конструкции на поведение пьезоэлемента можно учесть, например, вводя дополнительные параллельные ветви в схему модели Van Dyke. Аналогично модифицируется и модель Guan, образуя так называемую полную модель. Каждая последовательная RLC-ветка в этой модели физически соответствует одной резонансной моде. Однако при применении полной модели Guan возникают сложности при определении численных значений ее параметров в том случае, когда резонансные частоты пьезокерамики и конструкции близки или совпадают.

При разработке электрических аналогов электро-вязкоупругих тел пьезоэлемент моделируется различным образом.

В ряде работ [29–32] предлагается в качестве электрического аналога пьезоэлемента использовать его простейшую модель, представляющую собой постоянную емкость С 0 . Но при этом необходимо понимать, что пьезоэлемент ведет себя как обычный конденсатор с емкостью С 0 i только на частотах, далеких от резонанса.

В настоящее время эквивалентные схемы замещения с учетом влияния основной конструкции нашли особенно широкое применение в задачах, связанных с расчетом эффективности устройств для сбора и накопления энергии (energy harvesting) на основе пьезоэлектрических материалов как малых альтернативных источников энергии [33], в которых крайне важно понимать рабочую производительность, обусловленную механическим и электрическим взаимодействием. Сами устройства моделируются, как правило, консольной балкой [34–35] и сложными электрическими схемами. В настоящее время подход, основанный на замещении конструкции ее электрическим аналогом в форме эквивалентной электрической схемы, нашел особенно широкое применение в таких приложениях, в которых крайне важно понимать рабочую производительность системы, обусловленную механическим и электрическим взаимодействием [28, 33–34].

Поскольку эквивалентная электрическая схема отражает реальную конструкцию и ее динамические характеристики при определенных граничных условиях, существует большое количество эквивалентных электрических схем, являющихся электрическим аналогом рассматриваемых систем, ориентированных на решение конкретных задач, и перенос ранее разработанных другими авторами схем на конструкции другой геометрии и другое внешнее воздействие зачастую просто невозможен.

Несмотря на то, что эквивалентные схемы замещения не только пьезоэлемента, но и всей конструкции с пьезоэлементом применяются все чаще, например [22, 36–37], не найдено работ, в которых электрические аналоги электроупругих тел с внешними электрическими цепями применяются для нахождения оптимальных параметров внешних электрических цепей, обеспечивающих максимальное демпфирование колебаний на заданных частотах, на основе использования задачи о собственных колебаниях конструкций.

В рамках данной работы предложено осуществлять анализ динамических характеристик электромеханической системы, представляющей собой конструкцию с пьезоэлементом, к электродированным поверхностям которого присоединена внешняя электрическая цепь, на основе электрического аналога в виде эквивалентной электрической схемы, представляющей собой дискретную электрическую систему с сосредоточенными параметрами. Полученная дискретная система является полным аналогом исходной электромеханической системы с точки зрения частотных характеристик и протекающих в ней электрических процессов. Предложенный подход позволил существенно сократить время численных исследований и на их основе получить математические зависимости связи предельных величин, определяющих динамические характеристики рассматриваемых систем (границы диапазона изменения собственных частот колебаний, максимально достижимый показатель демпфирования, значение резонансной частоты системы при подключении резистивной электрической цепи), со значениями собственных частот колебаний исходной конструкции с пьезоэлементом в режимах холостого хода и короткого замыкания.

1.    Дискретный электрический аналог электроупругого тела с внешними электрическими цепями

При определении динамических характеристик конструкций, представляющих собой континуальную среду с элементом, выполненных из пьезоэлектрического материала, к электродированным поверхностям которого подключена внешняя электрическая цепь (электромеханическая система), не всегда удобно и целесообразно решать задачу о собственных колебаниях в полной континуальной математической постановке [5].

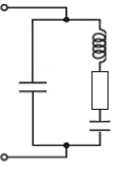
В расчетной схеме этой системы внешняя электрическая цепь представляет собой совокупность элементов с сосредоточенными параметрами и электрическими степенями свободы. Для уменьшения размерности решаемой задачи привлекательным является подход, позволяющий представить исходную конструкцию с присоединенным к ней пьезоэлементом в виде аналогичной дискретной системы с электрическими степенями свободы. Для этого предлагается воспользоваться моделью для описания кварцевого резонатора (рис. 1, а ), предложенной в 1925 году Van Dyke [8], распространив ее на все деформируемое тело с пьезоэлементом.

о

L i

R i

C i о

a                        б

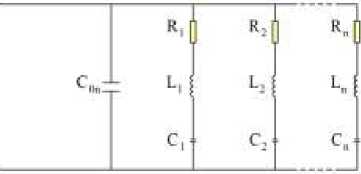
Рис. 1. Эквивалентная электрическая схема, предложенная Van Dyke [8] для кварцевого резонатора ( а ); электрический аналог электроупругого тела в форме эквивалентной схемы замещения ( б )

Fig. 1. Equivalent circuit proposed by Van Dyke [8] for a quartz resonator ( а ); equivalent circuits for electroelastic body in the form of equivalent substitution scheme ( b )

Данная модель (см. рис. 1, а ) представляет собой параллельное соединение последовательно соединенных емкости C , индуктивности L , сопротивления R и емкости пьезоэлектрика C . Индекс i указывает на то, что эта модель описывает поведение рассматриваемого объекта вблизи i -го резонанса. При исследовании динамического поведения конструкции не в окрестности какого-либо отдельного резонанса, а в некотором частотном диапазоне, в котором может находиться несколько резонансных частот колебаний, эквивалентная модель модифицируется путем добавления параллельно имеющимся элементам (ветвям) последовательных колебательных контуров (рис. 1, б ). В результате можно получить электрическую схему, описывающую динамику рассматриваемой системы в любом частотном диапазоне. Если рассматриваемое деформируемое тело с включением из пьезоматериала является упругим, то в эквивалентной схеме будут отсутствовать сопротивления R .

Рассмотрим математическую постановку задачи о собственных колебаниях электрического аналога упругого тела с присоединенным к его поверхности пьезоэлементом в форме эквивалентной электрической схемы.

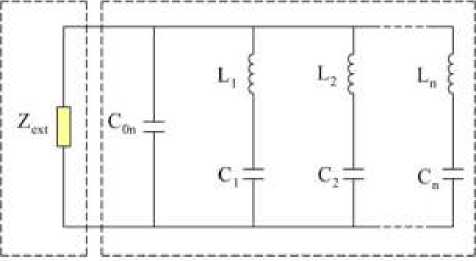
К электродированным поверхностям пьезоэлемента подключена внешняя цепь, состоящая из различным образом соединенных индуктивных ( L ) или резистивных ( R ) элементов, с общим электрическим импедансом Z^,. Предположим, что колебания тока во внешней цепи происходят с частотой колебаний всей электромеханической системы. Тогда схема электрического аналога, описывающая поведение дискретной системы (конструкция, пьезоэлемент и внешняя электрическая цепь) в диапазоне, включающем n резонансных частот колебаний, будет иметь вид, представленный на рис. 2. Здесь емкость C и параллельные ветви LC относятся непосредственно к упругому телу с пьезоэлементом, а элемент Z описывает внешнюю электрическую цепь.

Внешняя электриче- Упругая конструкция с пьезоэлементом ская цепь

Рис. 2. Эквивалентная схема электрического аналога электроупругого тела с внешней электрической цепью

Fig. 2. Equivalent circuits of an electrical analogue for electroelastic body with external electric circuit

Далее решается задача о собственных колебаниях электрического аналога рассматриваемой системы. На основании законов Кирхгофа для электрических цепей [38–39] i -й электрический контур C L C в данной схеме (см. рис. 2), образованный емкостью C с каждой параллельный ветвью C L , описывается дифференциальным уравнением относительно электрического заряда. В результате для n контуров имеем n дифференциальных уравнений (1):

2 n

• L.-O- +    Qi + У--- Qi = 0, i = 1, n .      (1)

i2                i                       j dt      Ci      j=1 C 0 n

Получим уравнения для внешней электрической цепи. Пусть внешняя электрическая цепь представляет собой последовательно соединенные сопротивление R и индуктивность L . Тогда уравнения баланса напряжений для контура внешней цепи будут иметь следующий вид (2):

T  d 2 q x , n   dq exl , у q j

L v ⁺ R--^- + g ^г         (2)

Подставляя в систему (1)–(2) решение вида q_t = q_Oie ^X1, получаем систему линейных алгебраических уравнений относительно неизвестных зарядов в ветвях эквивалентной схемы электрического аналога (3), где X = X„, + i X,„ - комплексная частота колебаний.

Re Im q0iX2Li+ qi-+g qj = 0, i = 1,n, Ci j=1 C 0 n q0 ext X* L„ + q0 ext XRex, + g Q0^ = 0.

j = 1 C 0 n

Здесь мнимая часть комплексной частоты Xta представляет собой круговую частоту колебаний, а действительная часть XRe - показатель демпфирования.

Из решения характеристического уравнения для данной системы относительно X получаем n+1 пару комплексно-сопряженных собственных значений. Исходя из физических соображений в дальнейшем рассматриваем только комплексные частоты колебаний с положительной мнимой частью X_ta и отрицательной действительной частью X_Re (обеспечивающей демпфирование колебаний).

Подробно математическая постановка задачи о собственных колебаниях для предложенного электрического аналога рассматриваемой системы приведена в [40].

При использовании эквивалентных электрических схем для анализа динамического поведения электро-упругих систем основной проблемой является определение значений параметров C L и C составляющих ее элементов. Для определения данных параметров предлагается использовать следующий численный алгоритм.

На первом этапе определяется статическая емкость C на основе решения статической задачи о деформировании конструкции c пьезоэлементом под действием приложенной разности потенциалов V с учетом заземления одной из электродированных поверхностей:

C 0 = Q^" . (4)

Здесь Q – значение суммарного электрического заряда, образующегося на незаземленной электродированной поверхности, при приложении заданной разности потенциалов V .

Далее находятся собственные частоты колебаний упругой конструкции с пьезоэлементом без внешней цепи в режиме короткого замыкания электродирован-ных поверхностей пьезоэлемента на основе решения задачи о собственных колебаниях при помощи любого пакета прикладных программ, например ANSYS. В результате решения получаем спектр собственных частот колебаний, на основе которого определяются искомые параметры C L и C .

Для упругого тела с включениями из упругого пьезоматериала все собственные частоты колебаний являются чисто мнимыми. Тогда параметры эквивалентной цепи C L и C для каждой резонансной частоты определяются следующим образом:

C Q "'1

Ci=| "TV" I ,  Ll=   (    \ 2 ,  C0 ‘ = C0 -S Ci(5)

s/ c )           CA^S/c )

где X\,_c - собственная частота колебаний конструкции с пьезоэлементом, работающим в режиме короткого замыкания (short circuit).

Количество колебательных контуров, необходимых для описания динамических характеристик электро-упругой конструкции, определяется на основе анализа сходимости получаемых результатов в выбранном для исследования диапазоне частот. Сходимость оценивалась по значениям собственных частот колебаний, полученным на основе решения задачи о собственных колебаниях электроупругой конструкции с внешней электрической цепью методом конечных элементов (МКЭ) [5].

При некоторых модах колебаний конструкции деформация прикрепленного к ее поверхности пьезоэлемента может либо отсутствовать, либо быть симметричной. В этом случае на его электродированных поверхностях не будет генерироваться электрический потенциал, необходимый для работы внешней электрической цепи. Поэтому на таких модах колебаний внешняя электрическая цепь ни при каких значениях параметров не может быть использована с целью управления динамическим поведением конструкции. Возникновение таких ситуаций можно предотвратить соответствующим подбором расположения пьезоэлемента на конструкции [41].

Проведенные исследования показали, что учет в электрическом аналоге контуров, соответствующих модам колебаний, при которых на пьезоэлементе не генерируется электрический потенциал, не влияет на точность получаемых результатов, но при этом увеличивает порядок разрешающей системы уравнений. Поэтому для дальнейшего удобства при построении электрического аналога рассматриваемой механической системы в форме эквивалентной электрической схемы контуры, соответствующие таким частотам колебаний, исключались из рассмотрения [40].

2.    Результаты численного моделирования

Достоверность определения динамических характеристик электромеханических систем на основе использования их электрического аналога подтвердим на двух примерах.

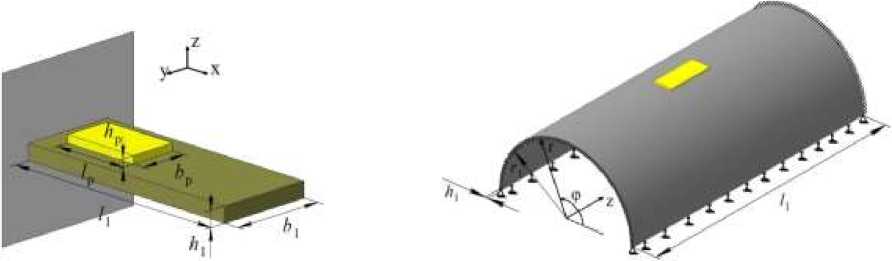
Первый пример – жестко защемленная по краю упругая пластинка (рис. 3, а ) с размерами l_x = 210 мм, b_Y = 26 мм, h = 0,5 мм. Пьезоэлемент выполнен в форме прямоугольника с размерами l = 50 мм,

Ь_р = 20 мм, h_p = 0,36 мм и расположен в 12 мм от закрепленного края пластинки симметрично относительно оси пластинки. Пластинка выполнена из материала со следующими физико-механическими характеристиками: модуль упругости E = 2 - 10¹¹ Па; коэффициент Пуассона v = 0,3 ; удельная плотность р = 7800 кг/м³. В качестве материала пьезоэлемента выбрана пьезокерамика PZT-4 с поляризацией в направлении оси z . Ниже приведены значения физико-механических характеристик: коэффициенты анизотропной матрицы упругих констант: C_n = C₂₂ = 13,9 -10¹⁰ Н/м²,    C₁₂ = 7,78 -10¹⁰ Н/м²,    C₁₃ =

= C₂₃ = 7,43-10¹⁰ Н/м²,     C₃₃ = 11,5-10¹⁰ Н/м²,     C₄₄ =

= 3,06 - 10¹⁰ Н/м², C₅₅ = C₆₆ = 2,56-10¹⁰ Н/м²; коэффициенты матрицы пьезоэлектрических модулей р₃ = р₃₂ = = - 5,2 Кл/м²,  р₃₃ = 15,1 Кл/м²,  р₅₂ = р₆₁ = 12,7 Кл/м²;

коэффициенты матрицы диэлектрической проницаемости e_u = е₂₂ = 6,45 -10 ^{- 9} Ф/м, е₃₃ = 5,62 -10 ^{- 9} Ф/м; удельная плотность р = 7700 кг/м³. Оси z соответствует индекс «3» у компонент матриц. Верхняя и нижняя поверхности пьезоэлемента электродированы.

В качестве второго примера рассматривается тонкостенная оболочка в форме полуцилиндра, жестко защемленная по торцам и свободно опертая по образующей (рис. 3, б ). Оболочка имеет следующие размеры: Г = 76 мм l = 300 мм, h = 0,25 мм. К поверхности оболочки прикреплен пьезоэлемент в форме сегмента кольца с размерами    т_р = 76,25 мм, Ф_р = 15,08°,

Н = 0,36 мм. Центр масс пьезоэлемента расположен на расстоянии 15 мм от защемленных торцов и смещен на 90° по угловой координате от свободно опертых образующих. Оболочка выполнена из упругого изотропного материала со следующими физико-механическими характеристиками: модуль упругости E = 1,96 -1011 Па, коэффициент Пуассона v = 0,3, удельная плотность р = 7700 кг/м3. Пьезоэлемент выполнен из пьезокерамики PZT-4. Направление поляризации совпадает с направлением оси r. Физико-механические характеристики в этом случае приводятся в цилиндрической системе координат: коэффициенты матрицы упругих констант: Cn = 11,5-1010 Н/м2, C12 = C13 = 7,43-1010 Н/м2, C23 = 7,78-1010 Н/м2, C22 = C33 = 13,9-1010 Н/м2, C44 = = C66 = 2,56-1010 Н/м2, C55 = 3,06-1010 Н/м2; коэффициенты матрицы пьезоэлектрических модулей рп =в2 = = -5,2 Кл/м2, р31 = 15,1 Кл/м2, р42=р63= 12,7 Кл/м2; коэффициенты матрицы диэлектрической проницаемости     eu = 5,62-10-9 Ф/м,     e22 = е33 = 6,45-10-9 Ф/м, удельная плотность р = 7700 кг/м3. Оси r соответствует индекс «1» у компонент матриц. Верхняя и нижняя поверхности пьезоэлемента электродированы.

Для обеих конструкций проведены численные расчеты и сравнения получаемых комплексных собствен- ных частот колебаний при помощи решения задачи о собственных колебаниях электроупругой конструкции с внешней электрической цепью методом конечных элементов [5] и предлагаемого подхода моделирования динамического поведения электроупругих конструкций с внешними электрическими цепями на основе их электрического аналога. Для решения задачи методом конечных элементов использовались трехмерные

20-узловые конечные элементы с квадратичной аппроксимацией узловых неизвестных. Для моделирования электрической цепи использовались специальные двухузловые конечные элементы с линейной аппроксимацией узловых неизвестных. Для получения решения использовалась численная реализация алгоритма МКЭ, приведенная в [5].

б

Рис. 3. Расчетные схемы конструкций с пьезоэлементом: пластинка ( а ) и оболочка ( б )

Fig. 3. Calculation schemes of structures with a piezoelectric element: plate ( a ) and shell ( b )

Количество возможных для определения собственных частот колебаний при расчетах методом конечных элементов в полной математической постановке задачи определяется размерностью разрешающей системы уравнений. При этом могут существовать такие моды колебаний, реализуемые при некоторых собственных частотах, на которых электрический потенциал на элек-тродированных поверхностях пьезоэлемента не генерируется. Для сравнения выбирались только те частоты колебаний, при которых генерируется электрический потенциал на электродированных поверхностях пьезоэлемента. Эти частоты колебаний пронумерованы в порядке возрастания их величины.

При расчетах с помощью электрического аналога рассматриваемой системы количество ветвей C L определялось степенью сходимости получаемых результатов к результатам, полученным при решении задачи о собственных колебаниях в полной математической постановке.

В табл. 1 приведено сравнение первой и четвертой собственных частот колебаний для пластинки и оболочки, полученных обоими способами.

В приведенных расчетах результаты, полученные двумя способами, как по действительной, так и по мнимой частям комплексных частот колебаний, отличаются не более чем на 1% для пластинки и на 2% для оболочки.

Таблица 1

Собственные частоты колебаний конструкций с пьезоэлементом и последовательной RL -цепью

Table 1

Eigenfrequencies of structures with a piezoelectric element and a series-connected RL -circuit

Номер λ	Параметры цепи		Расчет МКЭ		Расчет по электрическому аналогу
	Rext (кОм)	L ext (Гн)	Количество узловых неизвестных	λ Re + i λ Im 2 π	Число контуров n	λ Re + i λ Im 2 π
Пластинка
1	456,4	11054	5462	-0,85 + i ·13,79	1	-0,85 + i ·13,79
4	10,5	13,86		-22,21 + i ·408,83	8	-22,39 + i ·408,76
Оболочка
1	5,4	7,12	3808	-18,63 + i ·563,87	11	-19,05 + i ·563,78
4	1,0	1,3		-27,14+ i ·1239,19	27	-26,83 + i ·1239,75

Поскольку решение задачи с помощью электрического аналога позволяет многократно уменьшить требования к вычислительным и временным ресурсам, то это дает возможность на порядок увеличить количество рассматриваемых вариантов при численных исследованиях электромеханических систем в широком диапазоне изменения параметров внешней электрической цепи.

Присоединение внешней электрической цепи к конструкции с пьезоэлементом приводит к изменению ее спектра собственных частот колебаний. Изменение заключается в том, что чисто мнимые комплексные частоты колебаний упругой конструкции становятся комплексными, попарно сопряженными. При этом в спектр собственных частот колебаний в случае последовательной внешней резонансной электрической цепи добавляется еще одна дополнительная комплексная частота колебаний. Эта частота может существенно меняться при изменении параметров электрической цепи (осуществляя настройку внешней электрической цепи на заданную частоту). При сближении этой дополнительной частоты колебаний с собственной частотой колебаний конструкции с пьезоэлементом последняя также изменяется по величине.

Накопленная в ходе многочисленных исследований информация позволила выявить закономерности, позволяющие определить границы возможного влияния изменения параметров электрической цепи на динамические характеристики системы, на основе значений собственных частот колебаний конструкции с пьезоэлементом в режимах холостого хода λ и короткого замыкания λ при отсутствии внешней электрической цепи.

Во-первых, представляют интерес границы диапазона, в котором возможно изменение действительных частей собственных частот колебаний системы в зависимости от параметров внешней электрической цепи:

а) при резистивной R- цепи (состоящей только из резистора сопротивлением R ) изменение сопротивления вызывает изменение собственных круговых частот ко-

AX Im = X 0 i c -X S / c ;

б) при резонансной RL- цепи (состоящей из резистора сопротивлением R , катушки индуктивности L и конденсатора C, роль которого выполняет пьезоэлемент, обладающий емкостными свойствами) максимальное изменение i -й собственной частоты колебаний системы в области изменения параметров внешней цепи приближенно определяется формулой

AXL

i max       i min

= X Im - X Im ~ 2X

i s I c

' ^X 0 I c — ^X S I c

^X io I c ^+X S I c

где

λ

i max ^

Im ~

λ

ii

0 I c + ^X s / c

^{+ X} \ I c

I ^X 01c ^-X SIc

^X 0 I c ^+X S I c

ii i min   X o I c + X s I c

^X Im ~    2

V I X 0 1 c -X SIc λ

^{S I c} v X 01c +X SIc

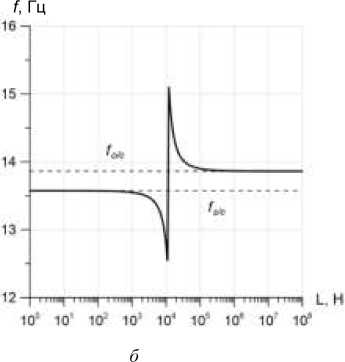
На рис. 4 приведены границы изменения первой собственной частоты колебаний пластинки при наличии резистивной (рис. 4, а ) и резонансной (рис. 4, б ) внешних электрических цепей. В случае резонансной цепи на графике приведено влияние изменения индуктивности при малом значении сопротивления (принято R = 10^–5 Ом). Таким образом, в случае резонансной цепи диапазон изменения i -й собственной частоты шире диапазона от λ до λ , указанного в работе [2].

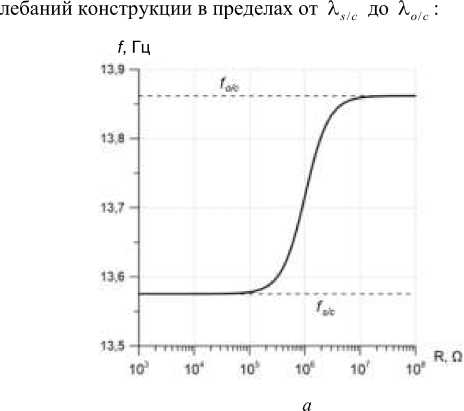
Рис. 4. Зависимости мнимой части первой комплексной собственной частоты колебаний пластинки f _Im = X^ 12 п от значения сопротивления для резистивной цепи ( а ) и от значения индуктивности для резонансной цепи при R = 10 -5 Ом ( б ); f,_Z c = X 0_Zc 12п , f_V c = X^ c 12n

Fig. 4. Dependences of the imaginary part of the plate's first complex eigenfrequency f _Im = X^ 12n on the resistance value for the resistive circuit (a) and on the inductance value for the resonance circuit at R = 10~⁵ Q (b), f _o/c = X_{o/ c} 1 2 n , f_s/c = X_s^_c 1 2 n

В качестве примера на рис. 5 приведен график изменения мнимой части первой комплексной собственной частоты колебаний оболочки (см. рис. 3, б ) в зависимости от изменения параметров внешней электрической цепи R и L , полученный с помощью моделирования динамического поведения электроупру-гих конструкций с внешними электрическими цепями на основе их электрического аналога.

а) при резистивной внешней цепи

λ

i max Re

-

^{λ i}o / c ^{-λ i}s / c ^;

б) при резонансной цепи

λ

i max Re

-λ ⁱs / c

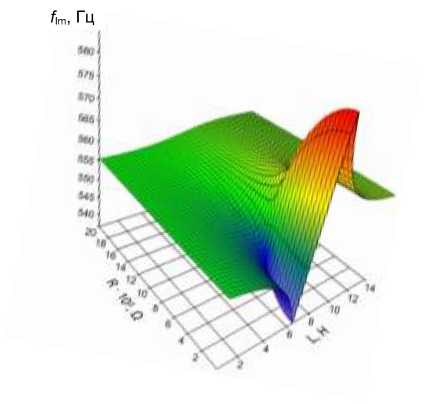
Рис. 5. Поведение мнимой части первой комплексной собственной частоты колебаний оболочки f λ /2 π

Im      Im в области параметров внешней электрической цепи R и L Fig. 5. The behaviour of the imaginary part of the shell's first eigenfrequency f λ/2π in the field of the external electric circuit parameters R and L

^{λ i}o / c ^{-λ i}s / c ^{λ i}o / c ^{+λ i}s / c

При использовании задачи о собственных колебаниях для построения оптимизационных алгоритмов, связанных с подбором параметров внешних электрических цепей для наилучшего демпфирования колебаний, одним из вариантов целевой функции может являться значение показателя демпфирования для какой-либо конкретной частоты. В этом случае знание максимально возможного показателя демпфирования позволяет как существенно упростить сам процесс оптимизации, так и позволяет рассмотреть сценарии, при которых достижения максимальной степени демпфирования не требуется.

Помимо этого, знание максимально-достижимого значения показателя демпфирования позволяет оценить, насколько удачно подобраны параметры внешней цепи при использовании аналитических формул.

Кроме того, обнаружено, что при достижении максимального демпфирования в случае резистивной цепи комплексная резонансная частота системы λ ⁱ может быть определена по формуле

λ

Из графика, приведенного на рис. 5, видно, что максимальное изменение действительных частей комплексных собственных частот колебаний в случае резонансной цепи наблюдается в области около нулевых значений сопротивления. Таким образом, основное влияние на ширину диапазона изменения действительных частей оказывает именно величина индуктивности.

Другая важная характеристика рассматриваемой системы – максимально возможный показатель демпфирования i -й моды колебаний λ ^{i max} :

i rez

^{λ i}o / c ^{-λ i}s / c     ^{λ i}o / c ^{+λ i}s / c

В табл. 2 для рассматриваемых конструкций (пластинка и оболочка) с пьезоэлементом и внешней резонансной RL -цепью приведены расчетные данные, полученные с помощью электрического аналога и по формулам (7) и (9).

Значения максимально возможного показателя демпфирования λ ^{i max} первой и четвертой мод колебаний пластинки и оболочки, полученные двумя способами, различаются менее чем на 3 %.

Таблица 2

Сравнение результатов, полученных по формулам (7) и (9) и на основе электрического аналога рассматриваемой системы

Comparison of the results obtained by equations (7), (9) and by the electrical analogue of the system under consideration

Table 2

Номер п/п	λ o / c	λ s / c	Диапазон изменения частот λ i min λ i max		Показатель демпфирования λ i max
			Электрический аналог	Формула (7)	Электрический аналог	Формула (9)
Пластинка
1	13,86	13,57	12,38–15,19	12,32–15,11	–1,42	–1,40
4	404,15	399,79	373,89–432,34	372,53–431,41	–29,83	–29,44
Оболочка

1	557,41	554,25	527,81–585,78	526,28–585,38	–29,91	–29,55
4	1293,42	1287,62	1233,496–1349,62	1229,47–1351,57	–59,22	–61,05

Заключение

В рамках данной работы предложен подход к анализу собственных колебаний электромеханических систем с распределенными параметрами, представляющих собой конструкции, содержащие элементы, выполненные из пьезоэлектрических материалов, к электродированным поверхностям которых присоединены внешние электрические цепи, на основе их электрического аналога, представляемого в форме эквивалентной электрической схемы замещения в виде дискретной электрической системы с сосредоточенными параметрами.

Продемонстрирована эффективность предлагаемого подхода для определения динамических характеристик упругих систем с пьезоэлементами и внешними электрическими цепями в сравнении с вариантом численной реализации задачи о собственных колебаниях электро-упругих тел с внешними электрическими цепями методом конечных элементов.

На примере определения собственных частот колебаний плоской и пространственной конструкций продемонстрированы достоверность и эффективность моделирования поведения электроупругих тел с внешними электрическими цепями на основе электрического аналога.