Решение задачи оптимизации освоения лесов с позиции логистики

Основная цель логистики состоит в минимизации затрат ресурсов и времени путем оптимального сквозного управления материальными и информационными потоками на пути от первичного источника до конечного потребителя. Принцип системности предполагает формирование интегрированной системы управления материальными потоками в рамках производственно-сбытовой системы. Системный подход в логистике предполагает рассмотрение хозяйствующих субъектов как комплекса взаимосвязанных подсистем. В этих усло- виях принятие частных решений без учета общих целей функционирования системы и предъявляемых к ней требований может оказаться недостаточным, а возможно и ошибочным. На рис. 1 приведен пример логистической цепи мультимедийной доставки лесопродукции конечным потребителям.

Современные требования лесного законодательства России и сертификация лесоуправления и лесопользования требуют организацию экологически и экономически сбалансированного, устойчивого лесопользования. По сути это та же система прослеживания и оценки всей цепочки движения лесной продукции от лесозаготовителя к потребителю, как и в системе транспортной логистики, но с точки зрения законодательной базы, экологии и охраны окружающей среды. При этом оцениваются и леса и лесная продукция на соответствие всем принципам и критериям устойчивого лесопользования.

Поэтому, прежде всего, нами была разработана, испытана и внедрена в проектную практику математическая модель [1, 2, 3, 4, 5, 7, 11] и соответствующее программное обеспечение [10] оптимизации величины расчетной лесосеки.

PP

2 Xm +1;p -X Xm;p - °’   (m = 1, d; P = 1P);

p=1

Xm+1;p — Xm;p - 0’      (m = I’d;P = ^);

mm

XXk;p ~ X П g-k+1;pPg-k+1;pSg-k+1;p + a^g-k+1;p^g-k+1;pSg-m;p k=1

(m = 1,d -1,d < g;p = 1,P);

m                              m - gg

X X ; p   ^ p ^ p X d - g + 1; p   P p X X j ; p ~ X ⁿ g - k + 1; p ^ g - k + 1; p^Si ; p ^{;   ( m} = ^g , ^d ; ^{d — g} ; ^p = 1, ^P );

i=1                                                    j=1

(1 - U^p X;d-g - Spmm;

X Z p X p ^ R ’

pd

F = XXXpkСр ^ MAX,(7)

p =1 k =1

где p - номер хозяйственной секции; P - число хозяйственных секций; X - расчетная лесосека i-го де-I; p сятилетия p-й хозяйственной секции; S - площадь лесосеки i-й возрастной градации p-й хозсекции; i; p q min Sp

-

минимально допустимая с экологической точки зрения площадь спелых лесов р -й хозяйственной

секции; С р – товарная продукция, которая может быть получена с 1 га р -й хозяйственной секции; ά – коэффициент, характеризующий интенсивность перехода лесов из одной возрастной градации в другую; β – коэффициент лесовосстановления; ή и μ – коэффициенты, учитывающие вероятность риска потерь, связанных с пожарами и потерь от лесных вредителей; Z _p – затраты на 1 га лесосеки в j- м десятилетии; R – финансовые возможности предприятия.

Здесь ограничение (1) характеризует требование неубываемости лесопользования, а ограничение (2) применяется только к лесосекам с хозяйственно ценными породами древесины, неубываемость которых с экономической и экологической точки зрения является весьма актуальной.

Для соблюдения требований о сохранении разнообразия видов необходимо исключить всякую возможность исчезновения некоторых пород в результате естественной или искусственной их смены, поэтому модель дополнена системой ограничений (5). В полученной модели в качестве целевой функции (7) принято требование не максимизации суммарной площади рубок, характерное для экстенсивного способа освоения природных ресурсов, а требование максимизации товарной продукции, более соответствующее интенсивному развитию и современным экономическим условиям.

Эта модель обеспечивает выполнение принципов непрерывного, неистощительного и неубывающего лесопользования. Однако, как показали наши исследования, ее использование без учета экономической и транспортной доступности ресурсов отдельных участков леса может дать неверные результаты при лесном планировании.

Анализ динамики лесовосстановления после рубок в нашей модели характеризуется коэффициентом β и основывается на результатах статистических исследования таких параметров, как что, где, когда и сколько вырублено и, как что, где, когда и сколько восстановилось после рубок. Кроме того, в модели учитываются возможные потери лесных ресурсов от различных негативных факторов – коэффициенты ή и μ .

На этих данных основывается начальный этап прогнозирования динамики лесного фонда, что должно являться необходимой составляющей математической модели.

Такой подход является одним из основных факторов, определяющих экономическую доступность ресурсов отдельных участков леса. Поэтому решение задачи прогнозирования запасов весьма актуально и является непременным условием реального соблюдения принципа непрерывного неистощительного лесопользования [6, 12, 13].

Для решения этой задачи экспериментально-аналитическими методами нами выведены специальные формулы:

• -    для хвойных:

Z = ( Z_tt 2 ) /(2 t_mt_i -1 2 ) - (38,06 - 0,539 1 + 0,0189 1 ²) - 5,55 *10^: exp N - 20,6 / N + 7,21; (8)

• -    для лиственных:

Z = ( Z_tt 2 ) /(2t_mt ²) - 1 /(25,89 *10 - 6 1 ² + 20,63 *10 3 ) - (5,55 * 10 " ³ exp N - 20,6 / N + 7,21, (9)

где Z – прогнозируемый запас древесины на момент рубки; Z t – запас древесины на лесоучастке по таксационным данным; t m -– возраст рубки; t – возраст древостоя на лесоучастке; N – ранг породы.

Они позволяют для любого участка леса при известном исходном возрасте древостоев только по одному измерению среднего фактического запаса древесины (при любом породном его составе и бонитете) прогнозировать этот запас к моменту рубки. Испытание этой формулы по таблицам хода роста дали положительные результаты. Величина расчетной лесосеки, на наш взляд, должна определяться с учетом экономической доступности лесных ресурсов, а не их наличия как такового, существующих и проектируемых транспортных путей, что практически отсутствует в современной практике. Определение расчетной лесосеки [2, 3, 4, 6, 8, 9, 14, 15] без учета экономической доступности участков лесного фонда приводит к получению значительно завышенных результатов. В частности, по некоторым оценкам, около половины эксплуатационных лесов Сибири являются недоступными по экономическим показателям. По Красноярскому краю доступными являются только около 30–50 %.

С другой стороны, оптимизация величины расчетной лесосеки должна производиться в тесной взаимосвязи с (определением) задачей экономической доступности и оптимизации транспортной схемы сети лесных дорог, с учетом очередности введения в эксплуатацию отдельных ее участков. В то же время интенсивность строительства дорог определяется финансовыми возможностями арендатора, напрямую зависящими от величины прибыли, которая может быть получена от реализации лесопродукции.

Нами разработана графоаналитическая модель и программное обеспечение [19, 20] автоматизированного проектирования оптимальной транспортной схемы лесных дорог, основанная на теории графов. Каждый участок леса представлен в виде вершины графа, а все возможные дороги, соединяющие эти участки леса, – ребра графа.

В основу этой модели положен алгоритм построения минимального покрывающего дерева. Данная модель позволяет учитывать наличие имеющихся дорог, топографические особенности местности (наличие рек, озер, болот, гор и пр.), экономическую доступность отдельных лесных участков. Для реализации данной модели было разработано соответствующее программное обеспечение, прошедшее апробацию и государственную регистрацию [8, 9].

На рис. 2 приведен упрощенный пример оптимальной транспортной схемы, полученной на базе вышеуказанной графоаналитической модели, где кружками с цифрами указаны условные участки леса. 11-й и 23-й участки леса не связаны с другими дорогой, так как в силу ряда причин (большая удаленность, небольшие запасы древесины, ее низкое качество и пр.) их разработка экономически нецелесообразна.

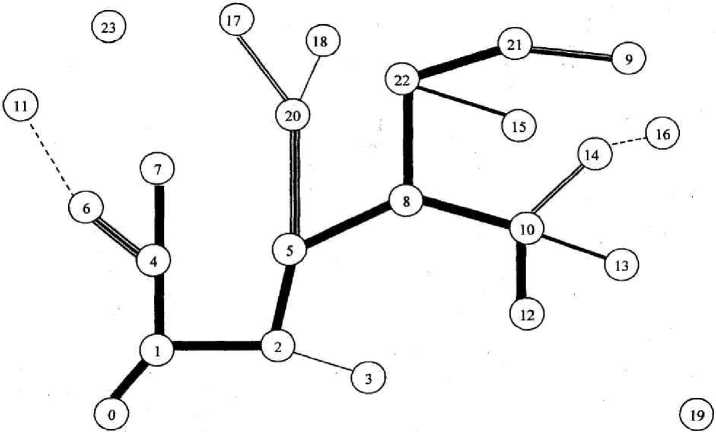
Рис. 2. Пример оптимальной транспортной схемы сети:

^^^н – дороги, ведущие к спелым и перестойным лесам (ввод в эксплуатацию этих дорог может понадобиться в первом расчетном периоде;

– дороги, ведущие к приспевающим лесам (ввод в эксплуатацию этих дорог может понадобиться во втором расчетном периоде);

– дороги, ведущие к средневозрастным лесам второй группы (ввод в эксплуатацию может понадобиться в третьем расчетном периоде);

– дороги, ведущие к средневозрастным лесам первой группы (ввод в эксплуатацию может понадобиться в четвертом расчетном периоде);

– дороги, ведущие к молоднякам второй группы (ввод в эксплуатацию может понадобиться в пятом расчетном периоде);

– дороги, ведущие к молоднякам первой группы

Эта схема составлена только с учетом распределения насаждений по возрастным градациям, без учета величины расчетной лесосеки. В данном примере условно преобладают спелые и перестойные леса. Для простоты будем считать, что все лесосеки, охваченные транспортной схемой, равноценны по своему количественному и качественному составу. Пусть, например, расчетная лесосека позволяет освоить в первое двадцатилетие не более четырех участков леса. Естественно предположить, что с экономической точки зрения осваивать следует в первую очередь ближайшие участки леса 1, 2 ,4, 7, или 1, 2, 5, 8. Таким образом, даже в таком простом примере уже на первом этапе появляется два альтернативных варианта.

Критерием оптимальности этой подзадачи должно являться требование получения максимальной прибыли, т.е. строить нужно ту дорогу, которая принесет больший экономический эффект, так как это в следующий временной промежуток позволит интенсифицировать процесс создания необходимой транспортной сети. Однако при этом необходимо учитывать и перспективность выбираемого направления. В данном примере дорога 1-2-5-8 совершенно необходима для дальнейшего освоения больших лесных массивов, в то время как дорога 1-4 позволит освоить только участки леса 6, 7 и 11, причем 11 понадобится только в весьма отдаленном будущем, так как хвойные насаждения на нем достигнут возраста рубки только через 100–120 лет.

Следует отметить, что экономическая недоступность отдельных лесосек может быть временной (рис. 2, участок 11), так как при увеличении возраста древостоев за пределы возраста рубки процесс увеличения запасов древесины продолжается, хотя прирост и замедляется. Это в свою очередь невозможно без решения задачи прогнозирования динамики лесного фонда. Следовательно, если при первоначальном расчете разработка некоторых лесосек оказывается нерентабельной, то это не означает, что они должны быть исключены из дальнейших расчетов. Очевидно их следует перевести в категорию “резервных“ лесов. Совершенно очевидно, что уменьшение в результате этого реальных запасов лесного фонда на величину экономически недоступных участков леса требует перерасчета величины годичной лесосеки.

В некоторых случаях экономически целесообразным бывает устройство грузосборочных участков. Оптимизация их месторасположения определяется методом “условного центра масс” [16, 17, 18]:

Е^^Кт."

=   ^_{= 1Zl}  ;

у  _ ^YiZiKm,

"     ^= tZ , где Xopt и Yopt – координаты грузосборочного участка; Xi и Yi – координаты исходных пунктов; Zi – запасы древесины на i-м лесоучастке; i – номер лесоучастка; n – число лесоучастков.

К т = ?.                                     (11)

н где Rф – фактический расход топлива на участке; Rн – нормативный расход.

При этом оптимизация транспортной схемы должна сопровождаться выбором мест расположения грузосборочных участков в местах смены транспортных средств.

Схема сети лесовозных дорог состоит из магистралей, веток и усов, отличающихся друг от друга величиной грузопотока, длительностью использования, а следовательно, качеством дорожного покрытия.

Очевидно, что чем выше качество дорожного покрытия, тем меньше затраты на вывозку. В то же время улучшение качества дорожного покрытия возможно только при существенном увеличении затрат на строительство дороги (рис. 3).

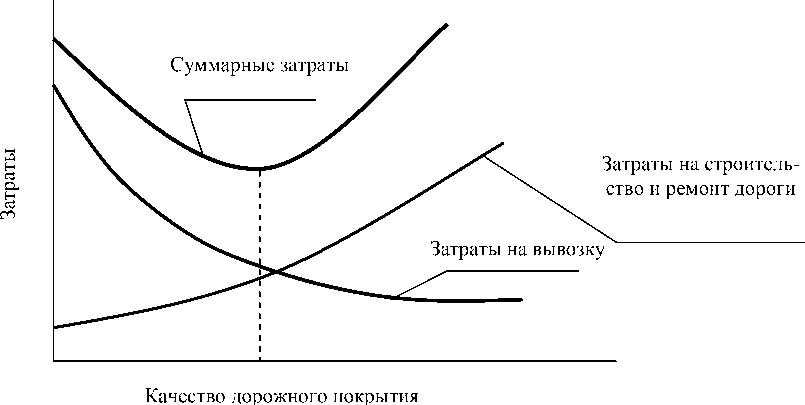
Рис. 3. Зависимость затрат от качества дорожного покрытия

Зависимость затрат на строительство и ремонт дороги от заданного ее качества видимо может быть описана уравнением (12):

Z пр =b + exp(-a * k),                                               (12)

где k – качество дорожного покрытия (качество дорожного покрытия количественно можно оценить, например, средней величиной сопротивления качению колес лесовоза или расходом топлива на 1 км пути); b – первоначальный минимум капитальных вложений на прокладку дороги, например, затраты на завоз техники к начальному пункту дороги; а – коэффициент, характеризующий эффективность капиталовложений.

Зависимость затрат на вывозку древесины от качества дороги можно описать функцией вида (13):

Z выв =b+exp (k * d),                                               (13)

где d – коэффициент пропорциональности, определяемый эффективностью применяемой технологии. Оптимальный уровень качества дорожного покрытия может быть определен из условия dZ = d (Znp + ZB^)

dp       dp

где Z – суммарные затраты на прокладку дороги и вывозку древесины; p – количественная оценка качества дорожного покрытия.

Очевидно, что в точке, соответствующей минимуму суммарных затрат, необходимо изменить технологию прокладки пути, а в точке, соответствующей этому минимуму суммарных затрат, необходимо изменить технологию строительства дороги в сторону улучшения ее качества. На рис. 4 это изображено пунктирными линиями.

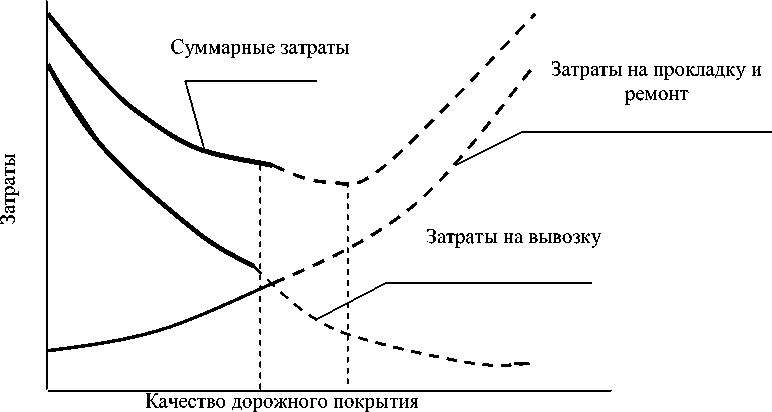
Рис. 4. Изменение затрат при изменении технологии строительства дороги

Качество дорожного покрытия определяется технологией (грейдерование, отсыпка, укладка бетонных блоков, асфальтирование), применяемой техникой и материалами (гравий, щебенка, асфальт и пр.) и, строго говоря, его зависимость от соответствующих затрат характеризуется прерывистыми линиями.

Однако при этом резко возрастает сложность решения задачи определения оптимального уровня качества дорожного покрытия и в первом приближении представляется вполне возможным и достаточным применение формул (13)–(14).

Таким образом, как было показано выше, решение задач прогнозирования запасов древесины на участках леса, оптимизации величины расчетной лесосеки и оптимизации транспортной схемы освоения лесов необходимо производить комплексно, т.е. в тесной связи друг с другом.

После построения схемы сети в соответствии с прогнозируемым грузопотоком необходимо определить качество дорожного покрытия [2, 15]. На последнем этапе данной логистической цепи производится выбор вида транспортных средств и транспортной схемы сети доставки лесопродукции потребителям [15].

Решения должны охватывать весь комплекс проблем ведения лесного хозяйства и лесопользования: законодательных, социально-экономических, технико-технологических, управленческих и других аспектов планирования и организации устойчивого управления лесным комплексом России. Это характерно для современного этапа развития логистики в развитых странах. Этот этап называется концепцией общей ответственности.

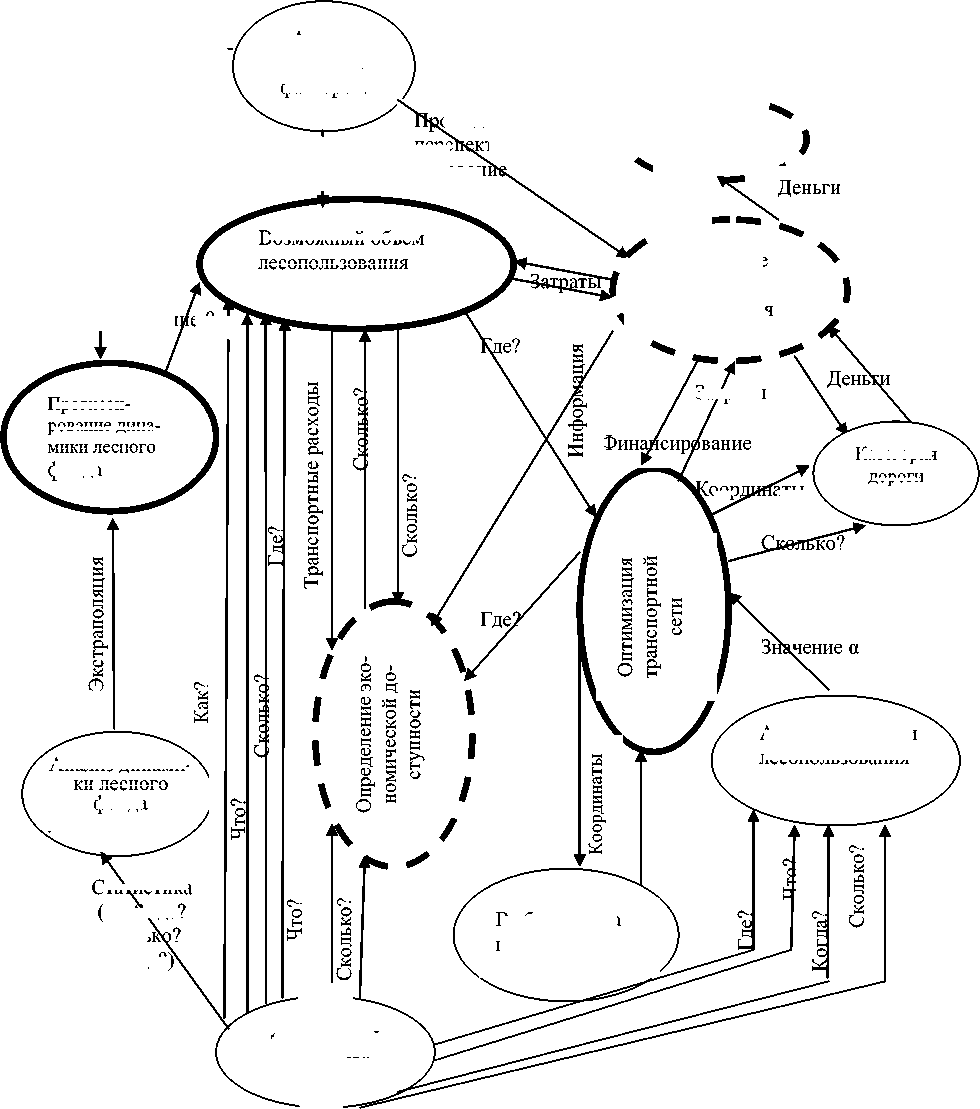
На рис. 5 приведена структурная схема организации системного подхода к решению задачи оптимизации лесопользования. Сложность и разветвленность этой схемы отражает сложность и многогранность поставленной задачи. Комплексные испытания полученных моделей были произведены на целом ряде конкретных арендных участков Ангаро-Енисейского региона и дали положительные результаты.

Прибыль

Значен огнозирование, тивное пла-

Затраты оор аты

Категория дороги

Статистика

Анализ динами ки лесного фонда

Возможный объем лесопользования

Прогнози- рование дина- мики лесного фонда перс нирован

Рис. 5. Структурная схема системного подхода к решению задачи оптимизации освоения лесов

Анализ внешних факторов.

Финансовое состояние

е β

(что? где?

сколь когда?)

Данные лесоустройства

предприятия

Анализ динамики лесопользования

Выбор пункта примыкания

Динамика лесопользования определяется стабильностью финансового состояния лесозаготовительного предприятия, а также оказывает весьма существенное влияние на фактические возможности освоения лесосырьевой базы в каждых конкретных условиях, на каждом временном интервале. Только объективная научно обоснованная и всесторонняя оценка сложившейся ситуации, определение стратегии и тактики развития лесного сектора на основе системного анализа и перспективных прогнозов позволят решать конкретные задачи, связанные с принятием оптимальных управленческих решений.

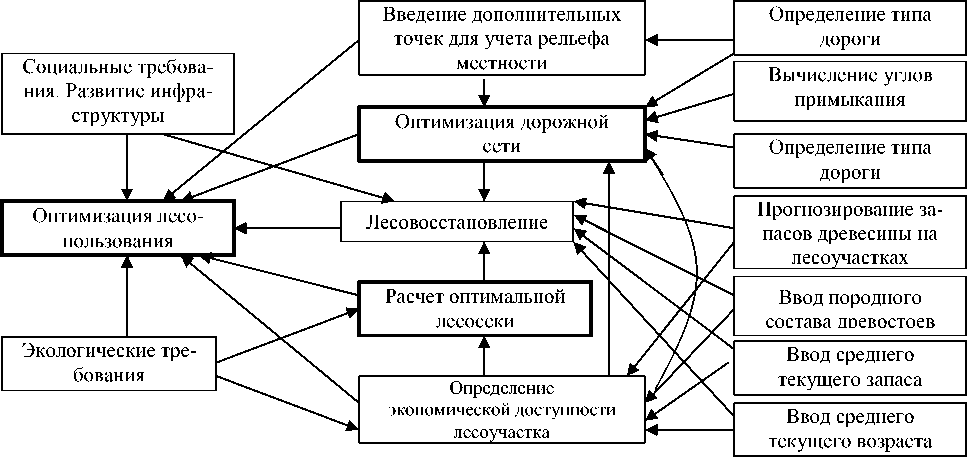
Рис. 6. Дерево целей решения задачи оптимизации освоения лесов

На рис. 6 приведено дерево целей, четко увязывающих все поставленные задачи в единое целое.