Решение задачи синдицированного кредитования методом динамического программирования

мо возвратить сумму кредита с процентами. Сумма вып

начиная с последнего. Оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом его последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Это основное правило динамического программирования, сформулированное Р. Беллманом, называется принципом оптимальности. Использование этого принципа гарантирует, что управление, выбранное на любом шаге,

лат В. рассчитывается следующим образом:

где г. - процентная ставка за кредит в z-м банке - в процентах в год, ах-управляющие переменные: х = 1, если в z-м банке нау'-й период берется кредит, и х..= 0 в противном случае, х . = (х, „., х^,. = 1,..., и. Предполагается, что максимальная сумма кредита, выдаваемая каждым

банком, одна и та же - норматив устанавливается Цент

робанком, - и ее величина приблизительно кратна 5, j = 1, ..., и. Размер кредита 5. будет складываться из потребности соответствующего этапа С . и суммы выплат за кредит предыдущего этапа В. Таким образом, сумму выплат можно записать в следующем виде:

является не локально лучшим, а лучшим с точки зрения процесса в целом.

Сформулируем нашу задачу в терминах динамического программирования. Физическая система 5, которой мы будем управлять, представляет собой группу банков с полученными от них средствами. Задание планировать на и этапов дает естественное членение процесса на и шагов. Ситуацию (состояние системы) перед началом j-го шага условимся характеризовать величиной 5 . . В состояние 5 система переходит из состояния 5 под воздействием управления х. Зависимость 5_у(5_у _ ₁, х) состояния системы нау-м шаге от состояния на (/-1)-м и управления в нашем случае имеет вид (3).

В качестве критерия оценки затрат на кредитование в

B j = ( j j )

m

S rX j

•

m

S Xj

i = 1

T j 365

Сумма кредита S . в этом случае составит

S j = S

m

S rx

i = 1

m

S xj

i = 1

•

T j - 1

.

результате примененного управления на каждом шаге будем использовать сумму выплат Ву, рассчитываемую по формуле (1).

Опишем в общем виде процедуру применения метода динамического программирования к решению этой задачи. Поскольку процесс динамического программи

рования разворачивается с конца, нам придется ввести

специальное обозначение для суммы выплат, формиру

ющейся за несколько последних шагов процесса:

+ C j .

r ( X j ) =

Требуется найти такой вариант последовательности

кредитования (в каких банках и на каком этапе должен быть получен кредит), при котором общая сумма выплат за весь плановый период обращается в минимум. При решении необходимо учесть, что на каждом этапе кредит может быть получен в банках отличных от тех, в которых был получен кредит на предыдущем этапе.

Поставленную задачу можно решать различными способами, а не только методом динамического программирования. Характерным для этого метода является определенный методический прием - процесс разделяется на ряд последовательных этапов (шагов) и произ

водится последовательная оптимизация каждого из них,

m

S rixij i=1

m

S X j

, i = 1

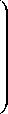
где В_и - сумма выплат по кредиту за последний

шаг,

В_{и1 и} - сумма выплат за два последних шага, В . _и -сумма выплат за последние (и^.+1) шага, начиная с j-го и

заканчивая и-м.

Процесс оптимизации начинается с последнего и-го шага. Пусть в начале и-го шага система находится в состоянии 5 . Тогда выплата за кредит на последнем шаге составит

B n ( S n , X n ) = S n ¹ +

.

Согласно уравнению (2) запишем выражение (4) в

виде

B n ( B n - 1 , X n ) = ( C n + B n - 1 ) f 1 + r ^ xC ^ ^T^- 1 ■       ⁽⁵⁾

V            /

Предположим, что значение В нам известно, и найдем условное оптимальное управление х*_п (номера банков). Это управление на последнем шаге находится как значение х , при котором величина В достигает минимума:

B n ( B n - 1 ) = min { B n ( B n - 1 , x n ) } ■ x_n

Так как значение оптимального управления в выражении (5) не зависит от того, какое значение примет В, то для удобства поиска ее можно принять любым неотрицательным числом. Заметим, что любые компоненты вектора хи могут принимать единичные значения, так как этот шаг единственный из всех, можно планировать так, чтобы он как таковой приносил наименьшие затраты. Таким образом, находим х*, при котором В принимает наименьшее значение.

Далее рассмотрим сумму выплат за 2 последних шага В _п. Для ее нахождения в формуле (5) представим В_и1 в виде выражения (2) и подставим вместо х ранее найденное х : И

BBx n - 1, n     n - 2 , n - 1

= B n ( C n - 1 + B n - 2 ) l 1 +

, x n

⁺ B n - 2 ) ^{1 +}

X

X 1 +

nn

Найдем х *_{и- 1}:

B * 1 ( B 2 ) = n -1, n n -2

= min { B , „ ( B ,x x_n ,)): V x 7 = 1 x. , = 0. n —1, n n —2 "  n —1             in         in —1

x n - 1

Как и на и-м шаге примем В за единицу При поиске х*_{п 1} необходимо иметь в виду, что его компоненты, совпадающие с удиничными компонентами х * , должны быть нулевыми.

Продолжая таким образом, можно найти условную оптимальную выплату за несколько последних шагов процесса и соответствующие им управления: В*_{п 2 и-1 п}(В_п-ъ), В* . , (В .) ит. д.

и- 3, и-Д и- 1, И- п-4^/

Если мы уже оптимизировали (/+1)-й шаг для любого исходау'-го, т. е. нашли В*_{/+1 п}(В / ) и х * , то условная оп-тимизация_/-го шага производится согласно общей формуле

B j , j + 1,..., n ⁽ B j - 1 )

= min {Bj,j+1,..,n (Bj-1, xj )} : VX7+1 = 1 xj = 0, xj где В пИВ.-1 х) - сумма выплат, достигаемая на последних шагах, начиная с/-го, при любом управлении нау-м шаге и оптимальном управлении на всех последующих. Таким образом определяется условная оптимальная сумма выплат на последних шагах, начиная с_/-го и соответствующее условное оптимальное управление.

Применяя последовательно, шаг за шагом, описанную процедуру, мы дойдем, наконец, до первого шага, на котором сумма выплат зависит только от управления, так как сумма кредита первого шага равна плановой потребности первого этапа:

B r..., n = ^min { B 1,..., n ( ^X 1 ) } .

x

В результате последовательного прохождения всех этапов от конца к началу найдены условные минимальные выплаты по кредитам на всех и шагах и соответствующие им оптимальные управления.

Чтобы найти суммы кредитов на каждый этап, необходимо снова пройти всю последовательность шагов -на этот раз от начала к концу. Для этого воспользуемся формулой (3), подставляя уже найденные нами х * и приняв 5₁ = С₁. Этот второй проход будет гораздо проще первого, потому что варьировать условия уже не придется.

В результате находится решение задачи: оптимальное управление х * = (х * ₁, х * ₂, .., х *_и ), сумма кредита 5 * = (5 * ₁, S*₂, .,5*_п) на каждый этап и минимально возможная сумма выплатВ * за весь плановый период.

Для оценки эффективности работы метода динамического программирования в данной задаче сравним его с полным перебором. Для ясности кратко приведем механизм полного перебора для данной задачи.

Сначала определяются все допустимые варианты кредитования (матрица вариантов кредитования). Каждый вариант представляет собой последовательность, в которой каждому этапу соответствует число - номер банка, участвующего в кредитовании. Число вариантов (число строк в матрице) к можно определить по формуле k = m (m -1) n 1, где т - число банков, участвующих в кредитовании, и - число этапов кредитования (число столбцов). Для всех вариантов по формуле (3) рассчитываются сумма кредита на каждый этап и сумма выплат за весь период. Вариант с минимальной суммой выплат принимается за оптимальный.

При реализации полного перебора необходимо вычислить сумму кредита (выплат) для каждого этапа. Количество вычислений в этом случае будет уПП = nm (m -1) n 1.

Рассчитаем количество вычислений суммы выплат при оптимизации с помощью алгоритма динамического программирования. На последнем шаге для определения оптимального управления необходимо вычислить т значений суммы выплат (т. е. определить выплату по кредиту в каждом из т банков). На всех остальных шагах вычисляется т-1 значение суммы выплат. Так как необходимо учесть, что вариант, при котором кредит выдается в одном банке подряд два этапа, недопустим. В результате имеем q дл = m + (m -1) (n -1).

Рассмотрим отношение ц_ПП к ц_ДП:

q дл _    nm ( m - 1) ^{n - 1}

q^ " m + ( m - 1) ( n - 1) "

Заменяя в знаменателе (т-1) на т, получаем, что трудоемкость полного перебора не менее, чем в (m -1)n раз больше трудоемкости алгоритма динамического программирования. Кроме этого, необходимо принять во внимание, что нахождение матрицы вариантов кредито- вания при полном переборе тоже требует значительных вычислительных ресурсов. В свою очередь, при динамическом программировании предварительного отбора допустимых вариантов не требуется: на каждом шаге идет простой перебор допустимых управлений.

Таким образом, эффективность приведенного метода при решении данной задачи очень высока. Благодаря этому метод динамического программирования позволяет находить решение и при большой размерности задачи с малыми вычислительными затратами.

• D.    A. Degterev, Е. Р. Pankov

THE SOLVING OF THE SYNDICATED CREDITING PROBLEM WITH A METHOD OF DYNAMIC PROGRAMMING

The solving of the syndicated crediting problem with a method of dynamic programming is suggested. High computing efficiency of the offered method in comparison with full search is shown.