Решение задачи создания ансамбля случайного леса для классифицирования моделей телефонов по ценовым категориям

Автор: Гущин А.В., Гущина О.А.

Статья в выпуске: 14 т.10, 2022 года.

Бесплатный доступ

В статье рассматривается создание и использование ансамблей случайного леса деревьев решений для предсказательной аналитики на примере решения задачи классификации восьмидесяти моделей телефонов с двадцатью признаками по четырем ценовым категориям. Проведен сравнительный анализ полученного решения с решением на основе метода деревьев решений.

Дерево решений, предсказательная аналитика, случайный лес решений

Короткий адрес: https://sciup.org/147250179

IDR: 147250179

Текст научной статьи Решение задачи создания ансамбля случайного леса для классифицирования моделей телефонов по ценовым категориям

На основе этих данных необходимо для каждой модели телефона спрогнозировать ценовую категорию (низкая, средняя, высокая и очень высокая).

Процесс решения задачи. Для хранения данных используется dataframe из библиотеки Pandas [1; 2] и массив из библиотеки NumPy, которые подключаются в начале файла. После загрузки данных можно просмотреть и их, и их статистическую информацию. Результаты этих манипуляций представлены таблицах 1–4.

Часть элементов выборки

№	battery_power	blue	clock_speed	touch_screen	wifi	price_rang e
0	842	0	2.2	0	1	1
1	1021	1	0.5	1	0	2
2	563	1	0.5	1	0	2
3	615	1	2.5	0	0	2
4	1821	1	1.2	1	0	1

1995	794	1	0.5	1	0	0
1996	1965	1	2.6	1	1	2
1997	1911	0	0.9	1	0	3
1998	1512	0	0.9	1	1	0
1999	510	1	2.0	1	1	3

Таблица 2

Типы всех использованных переменных

battery_power, Blue, dual_sim, Fc, four_g, int_memory, mobile_wt, n_cores, Pc, px_height, px_width, Ram, sc_h, sc_w, talk_time, three_g, touch_screen, touch_screen, wifi, price_range	int64
clock_speed, m_dep	float64

Таблица 3

Результаты описательной статистики

№	battery_power	blue	• • •	wifi	price_range
count	2000.000000	2000.0000	• • •	2000.000000	2000.000000
mean	1238.518500	0.4950	• • •	0.507000	1.500000
std	439.418206	0.5001	• • •	0.500076	1.118314
min	501.000000	0.0000	• • •	0.000000	0.000000
25%	851.750000	0.0000	• • •	0.000000	0.750000
50%	1226.000000	0.0000	• • •	1.000000	1.500000
75%	1615.250000	1.0000	• •	1.000000	2.250000
max	1998.000000	1.0000	• • •	1.000000	3.000000

Категориальные и количественные переменные

Категориальные	[]
Количественные	['battery_power', 'blue', 'clock_speed', 'dual_sim', 'fc', 'four_g', 'int_memory', 'm_dep', 'mobile_wt', 'n_cores', 'pc', 'px_height', 'px_width', 'ram', 'sc_h', 'sc_w', 'talk_time', 'three_g', 'touch_screen', 'wifi', 'price_range']

Перед передачей данных в будущую модель их разделили на признаки и классы. После разделения провели распределение данных на обучающую и тестовую выборки с параметром test_size=0.25, то есть три четверти данных передали в обучающую выборку, а одну четверть – в тестовую.

На следующем этапе воспользовались библиотекой scikit-learn для создания объекта классификатора случайного леса и выполнения его обучение на представленных данных [3-6]. Переменную params используем для хранения параметров ансамбля. Эти данные передаем в функцию создания экземпляра случайного леса решений, фрагмент которого представлен далее. Далее воспользовались функцией обучения с передачей тренировочных данных.

Для контроля результата после обучения модели случайного леса оценили следующие показатели эффективности полученного решения на обучающей и тестовой выборках: точность на обучающей выборке, точность контрольной выборки, OOB-оценка, AUC на обучающей выборке и AUC на контрольной выборке. Результат приведен в таблице 5.

Таблица 5

Результаты вычисления точности модели случайного леса решений

Метрика	Результат
Правильность на обучающей выборке	0.999
Правильность на контрольной выборке	0.880
OOB оценка правильности	0.89
AUC на обучающей выборке для RandomForest	1.000
AUC на контрольной выборке для RandomForest	0.982

В качестве примера спрогнозировали принадлежность первых пяти объектов к определенному классу с помощью функции forestClassifier.predict_proba(X_test[:5])). Результат представлен в таблице 6. Каждый столбец соответствует определенному классу (ценовой категории), а строка – определенной модели телефона.

Пример вывода спрогнозированных вероятностей принадлежности первых пяти модели телефона (таблица 1) к одной из четырех ценовых категорий

0.01039387	0.06722729	0.15937753	0.76300131
0.0517534	0.09618108	0.26739106	0.58467446
0.06692121	0.44428379	0.37681018	0.11198482
0.01541764	0.04722354	0.13160823	0.80575059
0.23304687	0.55828515	0.15961096	0.04905703

Дополнительно с вычислением метрики точности модели случайного леса решений, была вычислена матрица ошибок (рис. 1) и сформирован квалификационному отчет (рис. 2).

Матрица ошибок:

[ [112	б	0	0]
[ 13	102	11	0]
[ 0	20	105	9]
[ 0	0	11	111]]

Рис. 1. Матрица ошибок.

Классификационный отчет

	precision	recall	fl-score	support
0.0	0.90	0.95	0.92	118
1.0	0.80	0.81	0.80	126
2.0	0.83	0.78	0.80	134
3.0	0.93	0.91	0.92	122
accuracy			0.86	500
macro avg	0.86	0.86	0.86	500
weighted avg	0.86	0.86	0.86	500

Рис. 2. Квалификационный отчет.

Преимуществом случайного леса и дерева решений перед другими методами прогнозирования является возможность оценивания влияния определенных признаков на конечный результат. Для этой цели был введен параметр классификатора случайного леса решений в виде одномерного массива. Для увеличения его информативности пришлось отсортировать все признаки по степени влияния на модель. Результат приведен в таблице 7.

Показатели важности признаков случайного леса решений

1	ram	0.522775
2	battery_power	0.076009
3	px_height	0.055573
4	px_width	0.054512
5	mobile_wt	0.035392
6	int_memory	0.031938
7	talk_time	0.026818
8	pc	0.026318
9	clock_speed	0.025707
10	sc_w	0.025151
11	sc_h	0.024550
12	fc	0.021197
13	m_dep	0.020963
14	n_cores	0.019568
15	dual_sim	0.005946
16	wifi	0.005899
17	touch_screen	0.005887
18	four_g	0.005619
19	blue	0.005320
20	three_g	0.004857

Чтобы понять, насколько эффективен ансамблевый подход мы построили дерево решений, обучили на том же наборе данных и вычислили для него показатели эффективности. Результат оценки модели дерева решений различными метриками представлен на таблице 8.

Таблица 8

Результаты вычисления точности модели дерева решений

Метрика	Результат
Правильность на обучающей выборке	1.000
Правильность на контрольной выборке	0.836
AUC на обучающей выборке для RandomForest	1.000
AUC на контрольной выборке для RandomForest	0.876

Сравнив показатели эффективности обучения для случайного леса и дерева решений в таблицы 5 и 8, отметим, что точность первого больше на 0.044, а значение AUC на контрольной выборке лучше на 0.106. Следовательно, ансамбль деревьев решений эффективнее дерева решений.

Для анализа показателей важности признаков дерева решений оценивания влияния определенных признаков на конечный результат и получили данные таблицы 9. Из нее видно, что два последних признака (touch_screen и four_g) не влияют на прогноз (и для эффективности работы алгоритма их можно убрать). Так же, как и для случайного леса решений, для дерева решений абсолютное влияние имеет первый признак (ram).

Таблица 9

Показатели важности признаков дерева решений

1	ram	0.659793
2	battery_power	0.093422
3	px_height	0.091308
4	px_width	0.085851
5	mobile_wt	0.012314
6	talk_time	0.010347
7	sc_w	0.007392
8	sc_h	0.005382
9	fc	0.005496
10	pc	0.004757
11	m_dep	0.004418
12	n_cores	0.004289
13	three_g	0.003922
14	dual_sim	0.003846
15	clock_speed	0.003296
16	int_memory	0.002545
17	blue	0.001433
18	wifi	0.000989
19	touch_screen	0.000000
20	four_g	0.000000

Для понимания структуры дерева решений в ансамбле и в отдельности, мы их визуализировали и вывели в PNG-файл (рис. 3, 4).

Рис. 3. Визуализация дерева решений из ансамбля.

= 0.47

ss = 57

I, 19. 13. 0]

px_height <= 1.75 gini = 0.06 samples = 39 value = [60. 2. 0. 0] class = 0

= 0.62

=s = 25

8. 12. 7. 0]

ram <= -0.83 gini = 0.34 samples = 32 value = [53. 7. 6. 0] class = 0

gini = 0.0 samples = 2 value = [0. 0. 3. 0] class = 2

gini = 0.0 samples = 21 value = [50. 0. 0. 0] class = 0

gini = 0.0 samples = 37 value = [60. 0. 0. 0] class = 0

gini = 0.44

samples = 2 value = [1.2. 0. 0] class = 1

gini = 0.0

samples = 2 value = [0. 2. 0. 0] class = 1

gini = 0.0 samples = 2 value = [0, 0, 5. 0] class = 2

talk_time <= -0.65 gini = 0.5 samples = 63 value = [10, 62, 23,0] class = 1

0. 0]

gini = 0.0 samples = 4 value = [0. 7. 0. 0] class = 1

ram <= 0.03 gini = 0.42 samples = 6 value = [0. 7. 3. 0] class = 1

gini = 0.0 samples = 2 value = [0. 0. 3. 0] class = 2

fc<=-0.2

gini = 0.63

samples = 11 value = [3. 7. 6. 0] class = 1

sc_h <= 0.64 gini = 0.5 samples = 5 value = [3. 0. 3. 0] class = 0

gini = 0.0 samples = 3 value = [3. 0. 0. 0] class = 0

gini = 0.0 samples = 4 value = [7. 0. 0. 0] class = 0

gini = 0.0 samples = 2 value = [0. 0. 3. 0] class = 2

battery_power <= 0.3 gini = 0.51 samples = 6 value = [7.1.3, 0] class = 0

gini = 0.38

samples = 2 value = [0.1.3. 0] class = 2

gini = 0.44 samples = 3 value = [1. 2. 0. 0] class = 1

'px_height<= -0.71л gini = 0.63 samples = 21 value = [9. 15. 7. 0]

class = 1 ,

int_memory <= -0.45 gini = 0.46 samples = 15 value = [2. 14,4, 0] class = 1

px_height <= 0.37 gini = 0.61 samples = 6

value = [1.2, 3, 0] class = 2

gini = 0.0 samples = 3 value = [0. 0. 3. 0] class = 2

Рис. 4. Фрагмент дерева решений из ансамбля.

В каждом дереве решений узлы содержат: вопрос по одному признаков, по которому выполняется дальнейший выбор; неопределенность; количество прошедших образцов; отношение классов, прошедших через этот узел, выраженное в абсолютных числах; значение класса, большинство образцов которого прошли через узел (для листьев это прогнозируемое значение для всех элементов, попавших в него).

Так как листья являются заключительными прогнозируемыми значениями классификации, то они не содержат вопроса. При обработке нового элемента, нужно спускаться вниз по дереву, используя признаки элемента для ответа на вопросы. В конце элемент дойдет до одного из листьев и по значению листа определяется принадлежность к одному из классов.

Для повышения точности необходимо использовать оптимальные параметры. Самым простым способом их выявления считается метод сеточного поиска GridSearchCV с кроссвалидацией из библиотеки sklearn.model_selection. Суть метода состоит в том, что строит множество моделей с различными параметрами, обучающимися и сравнивающимися по эффективности. Оптимальным числом различных моделей ансамблей является произведение значения кросс-валидации и числа комбинаций выбранных параметров.

После прохода всех параметров, показанного на рисунке 5, получаем гиперпараметры для лучшей модели (рис. 6).

Fitting 3 folds for ea	ch of	4320 candidates..	totalling	12960 fits
[Para 1lei(n_jobs=-l)]:	Using backend LokyBackend with			8 concurrent workers
[Para 1lei(n_jobs=-l)]:	Done	52 tasks	elapsed:	3.8s
[Para 1lei(n_jobs=-l)]:	Done	216 tasks	elapsed:	19.3s
[Para 1lei(n_jobs = -l)]:	Done	466 tasks	elapsed:	42.5s
[Para 1lei(n_jobs = -l)]:	Done	316 tasks	elapsed:	1.2min
[Para 1lei(n_jobs=-l)]:	Done	1266 tasks	elapsed:	1.9min
[Para 1lei(n_jobs = -l)]:	Done	1816 tasks	elapsed:	2.7min
[Para 1lei(n_jobs=-l)]:	Done	2466 tasks	elapsed:	3,7min
[Parallel(n_jobs=-l)]:	Done	3216 tasks	elapsed:	4.9min
[Para 1lei(n_jobs=-l)]:	Done	4066 tasks	elapsed:	6.4min
[Para 1lei(n_jobs=-l)]:	Done	5016 tasks	elapsed:	8.0min
[Para 1lei(n_jobs=-l)]:	Done	6066 tasks	elapsed:	le.lmin
[Para 1lei(n_jobs = -l)]:	Done	7216 tasks	elapsed:	12,5min
[Para 1lei(n_jobs = -l)]:	Done	8466 tasks	elapsed:	15.Imin
[Para 1lei(n_jobs = -l)]:	Done	9816 tasks	elapsed:	18.0min
[Para 1lei(n_jobs = -l)]:	Done	11266 tasks	\| elapsed	: 21.2min
[Para 1lei(n_jobs=-l)]:	Done	12816 tasks	\| elapsed	: 24.7min
[Para 1lei(n_jobs=-l)]:	Done	12960 out of 12960 \| elapsed: 25.0min finished

Рис. 5. Результат вычисления гиперпараметров.

RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None, criterion='gini', max_depth=15, max_features='sqrt' max_leaf_nodes=None, max_samples=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=3, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=700, n_jobs=None, oob_score=True, random_state=None, verbose=0, warm_start=False)

Рис. 6. Результат вывода гиперпараметров лучшей модели.

Проведя эксперимент по увеличению точности показателей в зависимости от максимальной глубины дерева и количества признаков в узле получили данные, приведенные в таблице 10.

Таблица 10

Результаты показателей точности модели случайного дерева решений с различными гиперпараметрами

param_max_depth

param_max_features Точность

log2 0.718581

sqrt 0.719463

Продолжение таблицы 10

3	log2	0.775933
3	sqrt	0.775521
7	log2	0.836848
7	sqrt	0.837754
11	log2	0.844720
11	sqrt	0.844389
15	log2	0.844227
15	sqrt	0.845271

На рисунке 7 приведен график зависимости вероятности совпадения полученных решений с реальными данными от количества деревьев в случайном лесе решений.

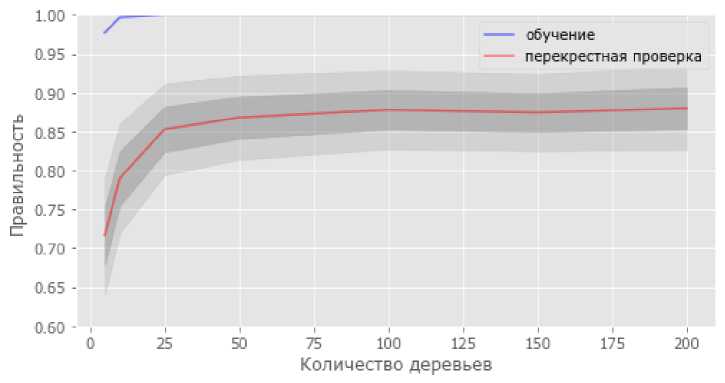
Рис. 7. График зависимости вероятности совпадения полученных решений с реальными данными от количества деревьев.

Заключение. В результате проведенного исследования были получены достаточно точные практические данные по предсказанию ценовой категории данных марок телефонов, а также сделан вывод о высокой эффективности использования ансамблей случайного леса и деревьев решений для предсказания классификации данных.

Список литературы Решение задачи создания ансамбля случайного леса для классифицирования моделей телефонов по ценовым категориям

Ансамблевые методы: бэггинг, бустинг и стекинг [Электронный ресурс]. - Режим доступа: https://neurohive.io/ru/osnovy-data-science/ansamblevye-metody-begging-busting-i-steking/(дата обращения: 03.11.2022).
Груздев А. В. Прогнозное моделирование в IBM SPSS Statistics, R и Python: метод деревьев решений и случайный лес. - М.: ДМК Пресс, 2018. - 642 c.
Открытый курс машинного обучения. Тема 5. Композиции: бэггинг, случайный лес [Электронный ресурс]. - Режим доступа: https://habr.com/ru/company/ods/blog/324402 (дата обращения: 03.11.2022).
Джоши П. Искусственный интеллект с примерами на Python: Пер. с англ. - СПб.: ООО "Диалектика", 2019. - 448 с.
A random forest classifier [Электронный ресурс]. - Режим доступа: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier (дата обращения: 03.11.2022).
Hastie Т. The Elements of Statistical Learning. - Springer, 2017. - 764 p.

Статья научная