Решения уравнения Лапласа в цилиндрических координатах, приводимые к двумерным гармоническим потенциалам

Одна из основных задач, решаемых при расчете корпускулярно-оптических систем (КОС), связана с вычислением реализуемых в них электрических и магнитных полей. При этом, как правило, приходится решать задачу Дирихле для скалярного потенциала, удовлетворяющего уравнению Лапласа. Расчет КОС значительно упрощается, если поле удается описать с помощью замкнутых аналитических выражений для потенциала. В случае двумерных полей декартову систему координат ( x , y , z ) можно выбрать таким образом, чтобы скалярный потенциал ϕ зависел только от двух координат, например x и y . Потенциал, описывающий такие поля, удовлетворяет двумерному уравнению Лапласа

1 д   д ф 1 д ф д ф .

--р —+—т—ф+—г = 0.

р д р   д р р ² д у    д z ²

В том случае, когда потенциал ϕ зависит только от ρ и ψ , получим уравнение

1 д д ф 1 д ² ф . р— + 2 —ф = 0.

р д р д р р д у

С помощью замены

П = ln р

уравнение (3) преобразуется в двумерное уравнение Лапласа

д2ф . дф = 0

д x ² д у ²

д 2ф + д2ф = 0 ду2 дп2

Решениями уравнения (1) являются гармонические функции декартовых координат x и y , поэтому в этом случае для расчета потенциала можно использовать мощный аппарат теории функций комплексной переменной (ТФКП).

В цилиндрической системе координат ( ρ , ψ , z ) уравнение Лапласа для потенциала ϕ имеет вид:

решения которого являются гармоническими функциями переменных ψ и η .

Потенциалы осесимметричных и трансаксиальных КОС в цилиндрической системе координат ( ρ , ψ , z ) зависят только от переменных ρ и z и удовлетворяют уравнению Лапласа:

д2ф + £ д ф + д 2ф = 0 д р2 р д р д z2

Наиболее общим методом решения граничной задачи Дирихле для уравнения (6) является метод разделения переменных. При этом потенциалы представляются в виде рядов функций Бесселя [1]. Однако эти решения из-за плохой сходимости рядов неудобно использовать для численных расчетов. В данной работе найдены простые приближенные выражения для потенциалов цилиндрической осесимметричной линзы и трехэлектродной трансаксиальной линзы, которые с хорошей точностью описывают поля этих систем.

КВАДРУПОЛЬ НА ЦИЛИНДРЕ

В том случае, когда потенциал ϕ зависит только от координат ρ и ψ , задачу можно решить и в декартовых координатах ( x , y , z ). При этом потенциал будет зависеть только от координат x и y . Рассмотрим квадрупольную электростатическую систему, в которой квадрупольное поле создается заданием потенциалов ± V на поверхности проводящего кругового цилиндра радиуса R , как показано на рис. 1. Измеряя линейные размеры в единицах R , получим граничную задачу на единичном круге, решение которой приводит к интегралу Пуассона для потенциала [2]:

1 — р 2². ^п           V ( t ) d t

Ф(P,V ) ^_^- J —-           .    ⁽⁷⁾

2 п * 1 + р - 2 p cos ( t - v )

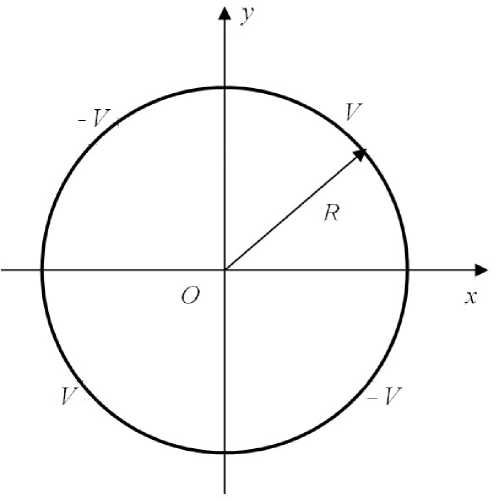
Рис. 1. Квадруполь на цилиндре

Здесь V ( t ) — угловое распределение потенциала на поверхности цилиндра. Перепишем выражение (7) в следующем виде:

^{1 -} P^P Ф( P,V ) ^_——^х 2 π

«I 2        ₍ ^{V (} t ^{) d}                  .

0 1 + p - 2 p ( cos t cos v + sin t sin v )

Используя следующую формулу

I

dx a + b cos x + csin x

(a - b) tg х+c arctg          2

2      2  22

найдем

2 V ф ( х , У ) =

π

1 + p ² + 2 х - 2 у

^{1 -} P^P

-

arctg V

1 + p + 2 х + 2 у

- arctg---------- 2-----

1 - P

+ arctg

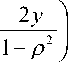
Здесь p = x¹ + у ². Легко проверить, что ф ( х ,0) _ ф (0, у ) _ 0, как и следовало ожидать, на осях координат потенциал обращается в нуль. Теперь найдем производные потенциала:

д ф _ 2V     2 (1 - P2) + 4x(1+ x - У)    _ дx п [(1 - p2)2 +[ 1 + p2 + 2(x - у)] 2

2 ( 1 - p ² ) + 4 x ( 1 + x + у )

( ¹ - P ²) 2 +[ ¹ + P ² + ² ( x + У ) ]

+------4 x 2,-----

( ^{1 - p 2} ) ^{+ 4} У ²

д ф _ 2 V ^2 (2 - ^{p 2} ) + 4 y ( l + x -2)_- l y""^П | ( 1 - p ² ) ² +[ 1 + p ² + 2 ( x - у ) ] ² "

2 ( 1 - p ² ) + 4 у ( 1 + x + у )

( 1 - P ² ) ² +[ 1 + P 2 + 2 ( x + у ) ] ²

+ 2 ( 1 - р ² + 2 у ²) ( ^{1 - р 2} ) ^{+ 4} У y

Найденные формулы описывают также и поле монополя, создаваемого частью цилиндрического электрода с потенциалом V и двумя взаимно перпендикулярными полуплоскостями xz и yz с нулевым потенциалом. Картина поля монополя представлена на рис. 2, где изображены эквипотенциальные линии поля, потенциал которых равен: 0.1 V , 0.2 V , …, 0.9 V .

Эквипотенциали находились путем численного интегрирования дифференциальных уравнений:

dу _ дф / фф     dх _ дф d х д х/ д у’ d у д у ф 03)

/ д х

Начальные условия для уравнений (13) задавались на прямой у _ х , и по формуле (10) находились такие значения x , при которых потенциал принимал значения 0.1 V , 0.2 V , …, 0.9 V . Эти значения x приведены в табл. 1.

РАЗЛИЧНЫЕ АНАЛИТИЧЕСКИЕ ПОДХОДЫ

Общее решение уравнения (6) может быть записано в виде следующего интегрального выражения [1]:

от

ф ( р , z ) _ j В ( Л ) e ^{1 X z}I ₀ ( Л р ) d X + const.    (14)

-от

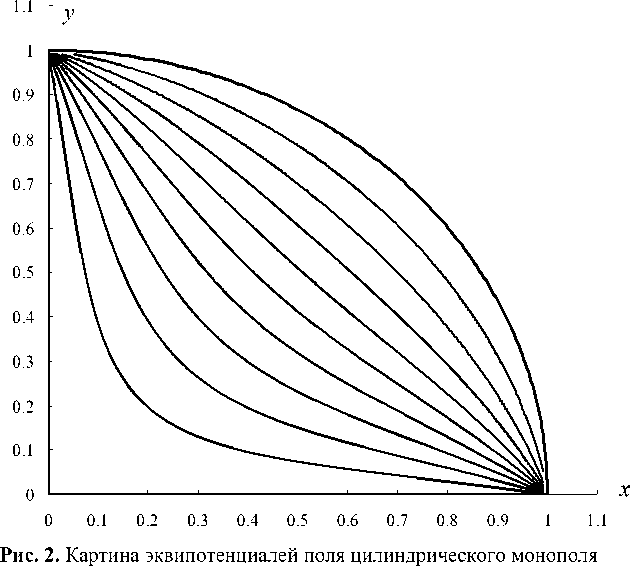
Табл. 1. Значения координаты x точек пересечения эквипотенциальных линий с прямой y = x

Пере-сечение	Эквипотенциали φ / V
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
х	0.19840	0.28143	0.34648	0.40307	0.45510	0.50475	0.55354	0.60274	0.65348

Вид функции В ( λ ) определяется граничными условиями, которым должен удовлетворять потенциал ϕ ( ρ , z ). Модифицированная функция Бесселя нулевого порядка, входящая в (14), может быть также представлена интегралом

π

I 0 (Xp ) = - [ e-^Xp cos ^e d в .        (15)

π ₀

В результате пространственное распределение потенциала произвольной осесимметричной системы однозначно определятся распределением потенциала на аксиальной оси U ( z ) = ф(0, z ) с помощью общей формулы Уиттекера [3]

1 ^π

ф ( p , z ) =—J u ( z + i p cos e )d в . π ₀

Эту формулу, а также приведенную ниже формулу (17) можно найти и в монографиях [4–7], где обсуждаются различные аналитические методы нахождения потенциала осесимметричных систем. Если известно распределение потенциала на оси U ( z ), то можно также использовать следующее

РАСЧЕТ ПОЛЯ МНОГОЭЛЕКТРОДНОЙ ОСЕСИММЕТРИЧНОЙ ЛИНЗЫ

Цилиндрическая осесимметричная линза, или зеркало, представляет собой круговой проводящий цилиндр, разрезанный плоскостями, перпендикулярными оси цилиндра (ось z ) в точках z_k [8, 9]. Эти плоскости делят цилиндр на электроды с потенциалами V k . Здесь k = 1,2,3, .„, N - 1. Такая линза схематически изображена на рис. 3. Здесь V_k - 1 , V_k и V_{k + 1} — потенциалы электродов, R — внутренний радиус цилиндрических поверхностей.

В приближении, когда зазоры между электродами считаются бесконечно узкими, потенциал такой ( N + 1)-электродной системы с хорошей степенью точности можно представить в виде [4]

1 ^N

ф ⁽ P , z ) = ( ^V N ^{+ V} 0 ) ⁺ Z Ф k ⁽ P , z ^{).       (18)}

²                  k = 1

Здесь ϕ_k ( ρ , z ) определяется выражением

Фk(p,z) = разложение потенциала, удовлетворяющее уравнению (6):

ф ( P , z ) =

24  6

= U ( z ) - U"^P + U ^{(IV) P}— U ^(VI) -^ + ...

4       64      2304

= - ( V k ^- V k - 1 ) ^arctg π

^sh I Th < z - ^z* )

πρ cos

2 R

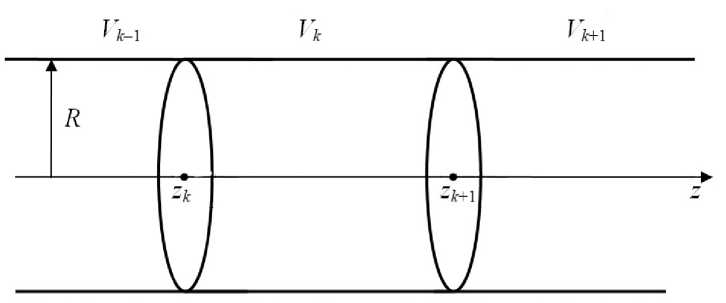
Рис. 3. Схематическое изображение цилиндрической осесимметричной линзы

^д Ф k __ 6

k

д x д p

-^^{( V} k - V k - 1 )

2 R

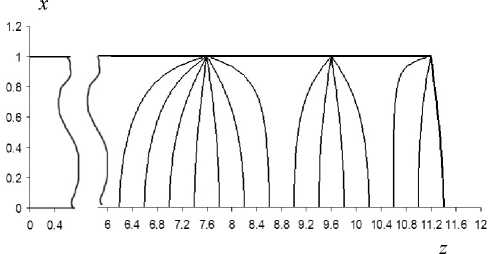
Рис. 4. Эквипотенциальный портрет поля четырехэлектродной КОС

Найдем аналитические выражения для частных производных. Используя формулу (21), получим:

■ | np ) ,2 л , x sin —- sh — z - z,

I 2 R J     3 R ^V k’

к

cos

² ^ 1+ sh² к 2 R J

2 π

--- ( z - z, 3 R ^{( k}

, (22)

)

^д Ф k д z

Здесь предполагается бесконечная протяженность первого электрода -да <  z <  z 1 с потенциалом V 0 и последнего электрода z_N - 1 <  z < да с потенциалом V_N . Выражение (19) является точным решением двухэлектродной граничной задачи для уравнения

= TR^(V k ^- V k - 1 )

3 R

[ np |    2n , x cos --- ch — (z - z, )

к 2 R J      3 R ^{( k} )

к

cos

^{2 np} 1+ sh² к 2 R J

2 π

— ( z - z,

3 R ^k

. (23)

)

д2 ф + д фр = 0

8 Р 2  д( V2z)

Для построения эквипотенциалей в плоскости xz , где у = 0, p = х , используем следующее дифференциальное уравнение:

d z д ф /д ф d x    д x / д z

и находится с помощью методов ТФКП. Нетрудно убедиться прямой подстановкой, что выражение (19) для ϕ_k ( ρ , z ) удовлетворяет уравнению (20).

Отметим, что уравнение (6) сводится к уравнению (20) в приосевой области малых ρ , т.к. в этой области, согласно (17), приближенно выполняется

8 ² ф   1 д ф    U "( z )

равенство —^ =--=--. Однако допол- д p2 p д p     2

нительный анализ показал, что более адекватной аналитической формулой для функций ϕ_k ( ρ , z ) является следующее выражение, которое лишь незначительно отличается от (19) следующей заменой: ( ^ z ^ 3 z /2 ). В результате

Ф к ⁽ p,^z ) = - ( V k ^- V k - i ) arctg π

^Sh 2R ^{( z} - z k )

πρ cos

2 R

.

Это уравнение интегрировалось численно по х от 0 до R . На рис. 4 приведена картина поля четырехэлектродной осесимметричной системы, у которой R = 1, z_x = 7.6 R , z ₂ = 9.6 R , z 3 = 11.2 R , V 0 = 1, V 1 = 0.3789, V 2 = 0.0710, V 3 =- 0.0863.

Расчет проводился для системы с бесконечно протяженными первым и последним электродами. Здесь первый электрод имеет достаточную протяженность, а последний электрод выполнен в форме замыкающей эквипотенциальной поверхности и имеет потенциал V 3 = - 0.0234.

В табл. 2. приведены данные, определяющие форму замыкающего электрода. На рис. 5 приведен также график распределения потенциала, рассчитанного по формулам (18) и (21), на оси z при p = 0 для той же электростатической КОС.

Табл. 2. Координаты поверхности замыкающего электрода

Ко-ордината	x / R
	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0.95
z/ R	11.4	11.397	11.390	11.377	11.360	11.336	11.311	11.286	11.255	11.227	11.213

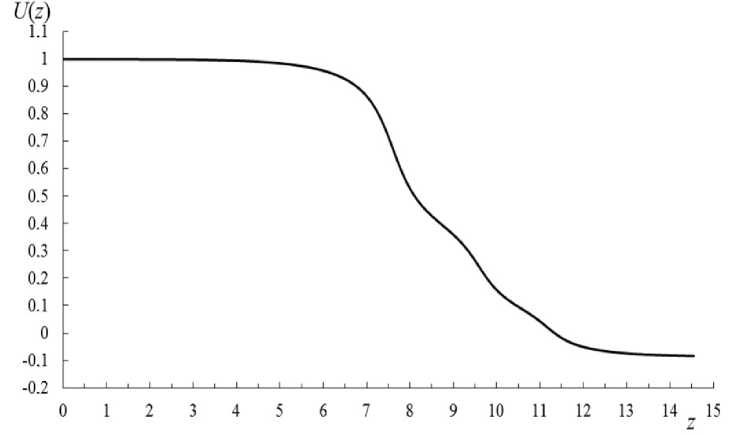
Рис. 5. Распределение потенциала на оси четырехэлектродной КОС

РАСЧЕТ ПОЛЯ ТРАНСАКСИАЛЬНОЙ ЛИНЗЫ

Трехэлектродная трансаксиальная линза представляет собой две параллельные пластины, разрезанные прямыми круговыми цилиндрами радиуса R1 и R2 , ось которых совпадает с осью z [10–12]. Такая линза схематически изображена на рис. 6. На рисунке показана также сопутствующая декартова система координат x, y, z. Начало декартовой системы координат находится в средней плоскости линзы, совпадающей с плоскостью xy; V0 , V1 и V2 — потенциалы электродов; d — расстояние между пластинами. Зазоры между электродами считаются бесконечно узкими. Вдали от краев пластин потенциал ϕ зависит только от переменных р = ^ x2 + у2 и z.

Вводя безразмерные переменные [12–16]

П = ln Р ,     Z = z ,           (25)

RR

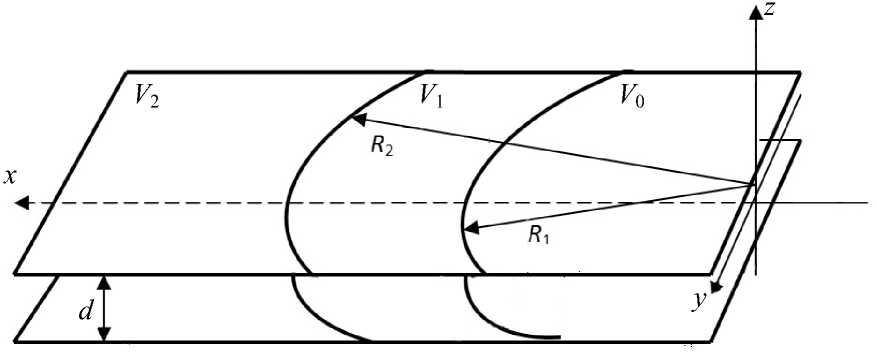
Рис. 6. Схематическое изображение трансаксиальной линзы

где R = д/ R 1 R 2 , получим следующее уравнение

для потенциала:

е -, п    ^Ф      . ^ф = 0.

д п d Z

удовлетворяет следующим граничным при z =± zo =±:

2 R

условиям

V для п <- п 0 ,

Гармоническая составляющая F ( η , ζ ) электростатического потенциала ф ( п, Z ) удовлетворяет двумерному уравнению Лапласа и является гармонической функцией безразмерных переменных η и ζ . Поэтому для расчета F ( η , ζ ) можно использовать аппарат теории функций комплексной переменной (ТФКП). Полученные таким образом аналитические выражения для потенциала дают хорошее приближение для потенциала ф ( п, Z ) , т-К- точно удовлетворяют заданным граничным условиям Дирихле и при р = R ( п = 0) удовлетворяют двумерному уравнению Лапласа.

В плоскости ηζ имеем электростатическую систему с двумерным полем, изображенную на рис- 7- В плоскости пZ потенциал ф ( п, Z )

ф ( п , ± Z 0 ) =1 V для — п 0 <  п < п 0 ,

V 2 для п >  п ₀-

В последней формуле п₀ = ln

R 2

. R 1

Уравнение (26) для потенциала можно решать методом последовательных приближений, взяв за нулевое приближение гармоническую функ- цию F(η, ζ),   удовлетворяющую граничным условиям (27). Чтобы найти потенциал F(η,ζ)

этой системы, отобразим полосу - Z0 ^ Z ^ Z0 комплексной плоскости ю =п + iZ на верхнюю полуплоскость плоскости w = и + i v с помощью следующего конформного преобразования:

V 0	V 1	ζ V 1	V 2
- п 0		ζ 0 η 0
		- Z 0	η
V 0	V 1	V 1	V 2

Рис. 7. Трехэлектродная электростатическая система с двумерным полем

v

V 2         V 1         V 1           V 0         V 0         V 1

V 1        V 2

–a 2          –1       –a 1         0       a 1         1

a 2

>

u

Рис. 8. Граничная задача в w- плоскости

Откуда

( nRa w = iexp ----

V d

.

φ x ( x , 0)

(nRnI ■ (nRZI u = - exp I-------I sin II

V d ) I d )(2

(nRnI v = exp I-------I cos II

V d ) V d )

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

-1.2

8.5        9        9.5        10       10.5       11        11.5       12        12.5       13       13.5

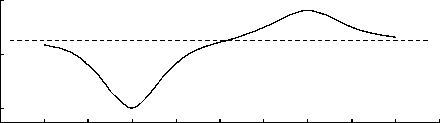
Рис. 9. Изменение производной потенциала вдоль оси х

В w- плоскости получаем граничную задачу, представленную на рис. 8, где верхним электродам соответствует область u <  0, а нижним — u >  0. Распределение потенциала в w -плоскости определяется следующим выражением:

F ( u , v ) = V₂ +

V -V

+ _0___1

arctg

V

u + a 1

v

arctg

- a ₁

₊ V - V 2

π

(

I arctg

V

u + a ₂

v

-

u - a ₂ I arctg-------- I .

v J

Здесь

( nRn I       1      ( nRn I a1 = exp I--- I, a2 =— = exp I------ I.    (31)

V d )        a 1      V d )

Возвращаясь к цилиндрическим координатам ρ и z , запишем также следующее выражение для потенциала:

Ф ( P,^z ) = V 2 ⁺

+ ( V - - V ) P i (P- , z , R ) + ( V - V 2 ) P 2 ( P , z , R ),    ⁽³²⁾

RR

где

π

₁           2cos z

P, (—, z, R) =—arctg------g—d7-, k                               πR

Ri         П ( "v—r (\ kdd

^— I - ^— I

V ^R k )    V ^R k )

k = 1,2.

Таким образом, получено простое аналитическое выражение для электростатического потенциала трехэлектродной трансаксиальной линзы.

На рис. 9 приведен график изменения производной потенциала ф х ( х ,0 ) вдоль оси х ( р = х ) для трансаксиальной линзы, у которой R 1 = 10 d , R ₂ = 12 d ; V 0 = 1, V 1 = 0.1, V ₂ = 0.6.

ЗАКЛЮЧЕНИЕ

Изучены подходы, позволяющие свеcти решение уравнения Лапласа для осесимметричных и трансаксиальных корпускулярно-оптических систем к расчету двумерных гармонических потенциалов, для нахождения которых используются методы ТФКП. Получены формулы, описывающие потенциал поля квадруполя с цилиндрическими электродами. Найдены простые аналитические формулы (18) и (21), которые с достаточно высокой точностью описывают электростатический потенциал поля многоэлектродной осесимметричной цилиндрической линзы или зеркала. Эффективность полученных формул обусловлена тем, что распределение потенциала вдоль оси симметрии U ( z ) достаточно гладкое (см. рис. 5) и поэтому старшие производные U ( z ) малы. В результате в разложении потенциала (17) основной вклад дают первые члены, для которых а ² ф 1 д ф    и"( z )

выполняется равенство —^=--=--, что д р р д р 2 приводит к двумерному уравнению Лапласа (20) для потенциала ϕ(ρ,z). При этом переход от двумерного потенциала к осесимметричному сводится к изменению масштаба вдоль оси симметрии.

Аналитические выражения для электростатического потенциала трехэлектродной трансаксиальной линзы (32), (33) также с хорошей точностью описывают поле линзы. Это связано с тем, что в области щелей, где происходит максимальный перепад потенциалов, с хорошей точностью выполняется двумерное уравнение Лапласа.