Resolver-to-digital converters with the arctangent function transformation

The scope of work is actual as it is devoted to energy informatics (energoinformational interaction) [1] of the electric drive [2] and mechartonic systems (MS) [3]. The analysis of publications devoted to the development, research and implementation of a dateware of the process of the conversion of energy in the functional movement of the working mechanism, possessing property of a chronotope, provides the following tasks:

• -    features of the resolver functioning and its construction [4–10];

• -    formation of the Common Dateware on the basis of the conversion corresponding to the general theory of relativity in terms of the postulate of time and space communication [11–16];

• -    as sensors at Common Dateware are used inductive [17], optical [18] and magnetic-field [19] sensors. Most widely used are Synhros and Resolvers (R), possessing remarkable properties and high performance criteria [2, 7].

Resolver is a 2-phase micromachine

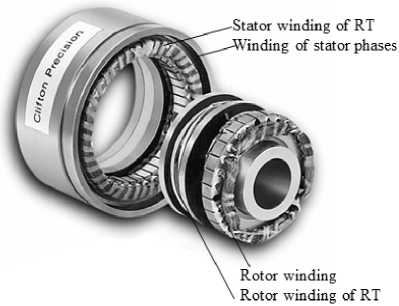
Resolvers are brushless type (Fig. 1) that is, the rotor excitation is ring transformer (RT) coupled to the shaft rotor winding. Many resolver applications operate with high speeds where the velocity error is significant source of measurement errors. Also, the signals of resolver are affected by the switching

Приборостроение, метрология

noise due to pulse width modulation (PWM) of the motor inverter [3, 4]. Paper represents a solution for measuring the resolver signals for electric drive application without being affected by the speed and the switching noise due to PWM of motor inverter.

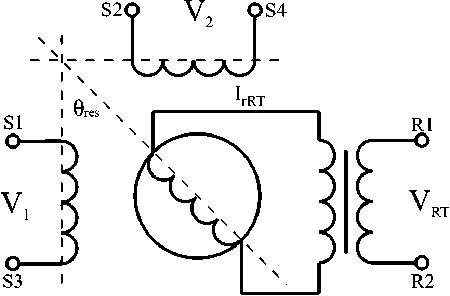
Fig. 1. The brushless classical resolver company Clifton Precision

The RT stator of brushless resolver (Fig. 1) is supplied from AC voltage V _RT = V_RTmsin ( Q _et + ^_e) of variable frequency Q _e and phase shift of ^_e. The RT stator and rotor currents are I _sRT and I_rRT = I_rRTmsin ( Q _et), respectively. Resolver is a 2-phase AC machine. So, the electrical equations for stator windings of this machine are:

V i = Rk + Lsk + s[(L_mCOS p _re s ® me )I rRT ] =

= RI_i + LsI _i

^L _m I _r RT ^pres ^ me

sin P res ® me

^{+ L}m^(cospres ® me⁾⁽ ^ ^IrRT^{) ;}

V i = RI₂ + LsI₂ + s[(L m Sin P res ® me )I rRT ] =

^RI2 ^{+ L}$k ^{+ L}m^IrRT ^pres ^ me ^{cos p}res ® me ^{+ L}m^(sinpres ® me⁾⁽ ^ ^IrRT⁾ ,

where Q _me is the mechanical speed; ® _me is the mechanical angle; p _res is the resolver number of poles; V_i, V₂; I_i, I₂ are the voltages and currents of stator 1 and 2 windings; R is the stator winding resistance; L is the stator winding inductance; L _m is the amplitude of mutual inductance of stator windings and rotor winding; s = d/dt .

In the no-load condition (high impedance of measuring circuits), for stator windings there will be no current and the current derivatives will be also zero (I_i = I₂ = sI _i = sI ₂ = 0). So, the equations (1) and (2) will be:

^Vi = ^Lm (cos p res ® meX^rRT ) ^{— L}m^IrRT ^pres ^ me (sin p res ® me ) ;

^V2 = ^Lm^IrRT ^pres ^ me^{(cos p}res ® me ) ^{+ L}m^{(sin p}res ® me⁾⁽ ^ ^IrRT^{) .}

The voltages (3) and (4) have two components: the first one (back-EMF) depends of excitation frequency Q _e (because I_rRT = I_rRTm sin Q _et), speed ( Q _me) and position ® _res = p_res ® _me, the second one (EMF of transformation) depends of frequency Q _e (because sI _rRT = I_rRTm Q _ecos Q _et) and position ® _res = p_res ® _me. This property of the signals V_i and V₂ allows to eliminate errors due to the speed Q _me. In the case of synchronous sampling of both signals V_i and V₂ when sin Q _et = 0 and cos Q _et = 1, the current I_rRT = 0 and its derivative is maximal: sI _rRT = I_rRTm Q _ecos Q _et = I_rRTm Q _e. So, in (3) and (4), the back-EMF components will be absent and EMFs of transformation will be only position dependent with maximal amplitude V n = L _m I _rRTm Q _e :

^Vi = ^Lm^{(cos p}res ® me^)IrRTm ^ e ;

^V2 = ^Lm^{(sin p}res ® me^)IrRTm ^ e ^.

From (5) and (6), the angle ® _me = ® _res/p_res may be calculated using standard software decisions.

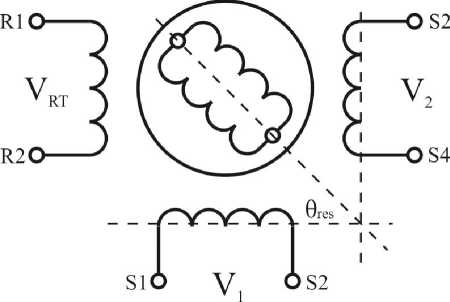
Variable reluctance resolvers (VRR) have no windings on the rotor. Their primary and secondary windings are all on the stator, but the saliency (exposed poles) of the rotor couples the sinusoidal variation in the secondary with the angular position Fig. 2) [5, 6].

Fig. 2. Variable reluctance resolver (reductosin)

The structure of the RDC with digital signal processor

Converter realising the proposed method by DSP comprises (Fig. 3): exciting generator EG , DAC and analog voltage inverter AVI for R excitation; differential amplifiers DA 1 and DA 2 conditioning resolver output signals; ADC for converting of analog signals V _i and У₂ into digital form D _i and D ₂ ; decoder software DSW for calculating of resolver angle 0 _res = ® _me p _r es from D_i and D₂.

RDC (Fig. 3) is capable of outputting a good resolver signals two times per excitation period without being affected by the motor speed and by the switching noise due to a PWM signal of an inverter. In the tested system, the 14-bit AD converter for data conversion was used. That means (4V/5Vyi6392= 13113 bit resolution for peak-to-peak of the measured signal. There are 360 x 60 x 60" (arc seconds) in the 32 periods (2 times peak-to-peak) of the resolver with 32 poles signal. So, one bit (resolution) of the ADC corresponds to 1,544" (arc seconds).

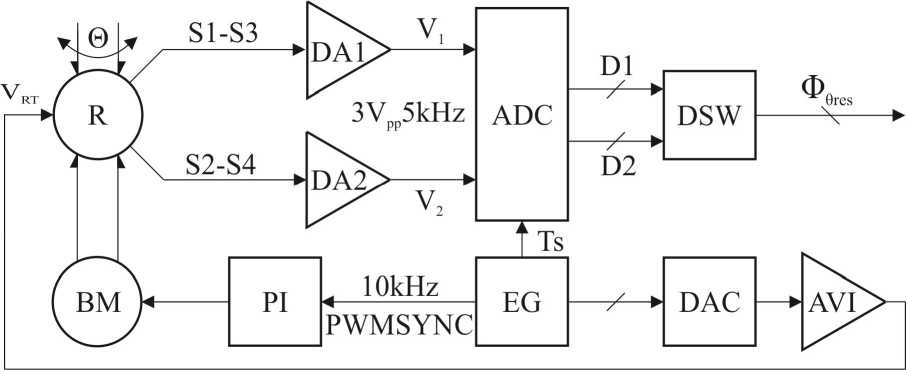
Fig. 3. Structure of the RDC with digital signal processor

An experiment has been set-up in order to validate the proposed solution. In this experiment, the modulation signal VRT and PWM noise were completely disappeared from the digital signals Di and D2. For what concerns the accuracy of the position measurement, a comparison between the processed resolver data and the incremental encoder data has been performed. The tests were done with mechanical speeds of 0,01 rad∙s–1 and 50 rad∙s–1 respectively. Very small differences between the two measurements were achieved. An off line calculation allowed to evaluate that the overall measurement error of the proposed RDC was contained within the 12 bit ADC error (6 arc seconds of the rotating angle) and was speed independent.

The resolver and RDC working principle of is as follows Fig. 4.

Приборостроение, метрология

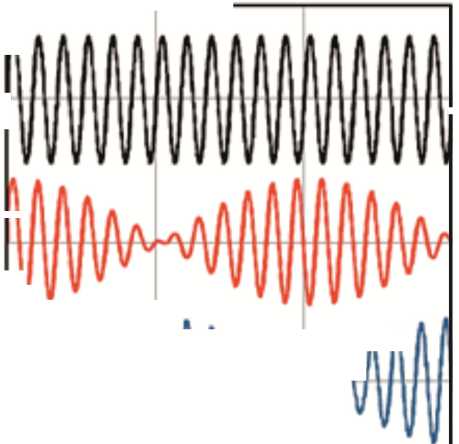
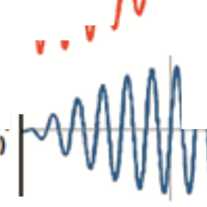
The two output signals are modulated by the sine and cosine of the shaft angle. A graphical representation of the excitation signal and the sine and cosine output signals is shown in Fig. 4a. The sine signal has maximum amplitude at 90° and 270° and the cosine signal has maximum amplitude at 0° and 180°.

On the Fig. 4b the excitation current derivative sI rRT , the PWM synchronism signal (PWMSYNC), sampling signal periods T s , cosine signal of position cospres θ me , output voltage V 1 and digital signal D 1 of 32-pole pair resolver after AD conversion by the motor speed of 937RPM and T s = 100 µ s.

=■■1 O’             90’            180’           270’

co^Pr*^) D1 -L.I.R^a.eoKp,,,©™.) PWMSYNC 0         2T.       4Г.        6T.        8T.

Fig. 4. Resolver and RDC working principle

The important feature RDC with digital signal processor

The first important feature of the used method is tuning of excitation voltage V RT zero in the sampling period ( T s ) of DSP for getting the maximal amplitude of resolver output signals V 1 and V 2 in the sampling moments T s . This tuning is done by the phase shift of V RT in the sampling period of the DSP during slow rotation of the motor. Tuning is finished by the maximum amplitude of signals V 1 and V 2 in the sampling moments T s . Such procedure gives in the sampling moment the extremum of derivative of resolver rotor current sI rRT , zero of resolver rotor current ( I rRT = 0) and zero back-EMFs in V 1 and V 2 – see (3) and (4).

The second important feature of the used method is synchronisation of PWM synchronism signal PWMSYNC with founded moment of resolver excitation. The PWM synchronism signal leading edge is tuned to get the minimal noise of measured signals. So, the system measures the resolver signals without being affected by the switching noise of inverter PWM . This phasing avoids the PWM interference on the resolver signals.

The third important feature of the used method is double sampling per excitation period. Position data D1 and D2 are read each sampling period at the time moments when the output signals amplitude is maximal. By the next sampling, the position data D1 and D2 are read as – V1 and – V2. So, digital signals D1 and D2 after conversion will have the amplitude modulated waveform of the exciting signal corresponding to the rotating angle ©res = ©mepres of the resolver as shown in Fig. 4b.

It is possible to calculate the angle, using a large number of known algorithms and various hardware [2, 3]. The simplest of these algorithms is a four-quadrant arctan signal conversion: © me P res = arctg^ l /^).

Calculation of the function arctg(β) by algorithmic and tabular methods

The series expansion of the function arctg(β) is carried out on [17]:

arctg ( P ) =f ( - 1 ) k -P 2 k ^{+ 1} /( 2 k + 1 ) .

k = 0

In the range of angles from 0 to 45 degrees for resolution of 20 bits 5 first members of a row are enough, taken with a 32-bit accuracy. Thus, after the measurement with the ADC, the calculation of the angle and its representation in the form of 0 to 1 for values from 0 to 2π takes 2 operations of normalization, one division, 5 multiplications, up to 8 additions and to 7 logical transitions on a short address. In total, no more than 40 cycles of a processor such as ARM Cortex-M3. For reduction of calculations Heron's formula is used. The calculations are integer (32 bits) with the normalization of up to 16 bits.

At calculation by the tabular method, the oktant with a required angle is determined by measured values of Vsin and Vcos and on the relation of values | Vsin | and | Vcos | the required angle is calculated by one of formulas [17]:

to Vsin > 0 and Vcos > 0 and to Vsin > 0 and Vcos > 0 and to Vsin < 0 and Vcos > 0 and to Vsin > 0 and Vcos > 0 and to Vsin > 0 and Vcos < 0 and to Vsin > 0 and Vcos < 0 and to Vsin < 0 and Vcos < 0 and to Vsin < 0 and Vcos < 0 and

Vsin I < I Vcos |, then ф = в,

Vsin I > I Vcos |, then ф = п/2 - в, Vsin I > I Vcos |, then ф = - в, VsinI < | Vcos I, then ф = -п/2 + в Vsin | > | Vcos I, then ф = п/2 + в, VsinI < | Vcos |, then ф = п - в, Vsin I < | V cos|, then ф = -п + в, VsinI > | Vcos |, then ф = -п/2 + в

where β – an angle in the range of 0…45 degrees (0…π / 4).

Further the value of tg(β) = |Vsin| / |Vcos| is calculated and according to the table, depending on tg(β1), the value of β1 is found, where tg(β1) – the nearest smaller tabular value of a tangent of angle, and a required angle

β = (tg(β) –tg(β1))(C0 + C1∙β1 + C2∙β1), where C0, C1, C2 – correction coefficients of correction of the algorithm error function. Such method provides resolution of 16 bits at the table size in 256 values.

Resolver-to-Digital Converter with arctangent ROM

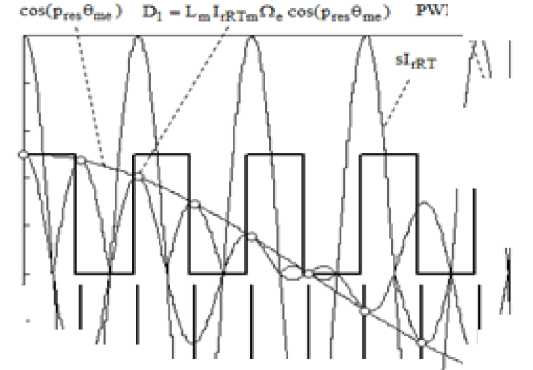
Application of DSC (Fig. 3) or ARM to evaluate the function β = arctg β within an octant in the algorithmic or tabular way leads to the reduction of the converting rate. Therefore, RDC with ROM should be preferred in high-speed MS. In MS, where “autophasing” [2] is not required, information on movement for self-switching of the electric motor can use the simplified algorithm of converting with arctg ROM. The offered [10] actantial representation of a full range of transformation, instead of a quadrant, at an equal speed allows to form additionally 3 highest weight discharge angles © .This is important in case of creation of a two-speed RDC, in which an additional bit is used for the matching of fine and coarse reading of MS. Speed of the conversion of output signals of resolvers to the digital equivalent of movement is also defined by speed of ADC of the relation of segments of tension in an octant.

In the scheme shown in Fig. 5 in the first stage output signals of resolver R are converted to a code of a tangent of angle tg P = V s /P c , where p - the angle of rotation 0 , given in the first octant. Simultaneously, the formation of three high-order digits of the angle Ф₀ is carried out. RDC works as follows. Two signals, proportional to the current value of sin S and cos C of the angle 0 , arrive on inputs of the analog switchboard and the detector of octants DO .

Their preliminary conversion is carried out either by individual demodulators DM of output signals of the resolver R or by peak detectors of the “memory access” type [10]. Three high-order digits of the code of the angle 0 are formed from the number of the octant. By comparison of output signals of the resolver R with each other and with a zero-level number of the octant is defined, which contains