Resource Provisioning for Routing with Priorities

Published Online October 2013 in MECS DOI: 10.5815/ijcnis.2013.12.02

Mobile networks have gained recent popularity due to their ease of access. More subscribers are switching from wired to wireless networks. Network designers need to upgrade the existing mobile communication systems to meet the ever increasing demand. To maintain Quality of Service (QoS), designers develop efficient call scheduling and routing techniques for the increasing traffic and reduce congestion at the same time. To guarantee QoS even during peak call rates, several techniques are employed such as – Call admission control, Traffic policing, resource provisioning, load balancing. Typically at a given cell site, the operations team continuously monitor the accessibility and retain-ability parameters of the calls. To handle sudden rise in demand/traffic operators deploy cellular on wheels (micro-cells) to supplement existing cell capacity. However this requires continuous monitoring and has scope of human error. A better approach would be to learn how call arrival rates change as a function of time (diurnal pattern) and use this knowledge to automate the process.

Provisioning is the process of preparing and equipping a network to allow it to serve new requests to its users. Resource provisioning is the process that supplements additional resources (servers/routers) required to handle a peak call rate so that QoS requirements can be met even during the peak workload. Different statistical techniques to predict peak call rates for an interval has been investigated. The predicted peak call rate is used as an upper bound to the worst case call rate and is provisioned for in advance. Thus predictive provisioning attempts to make arrangements for future variations in call rate. However, any prediction technique cannot be 100% accurate. Further, some call patterns are inherently unpredictable. For such cases, it is better to react accordingly to observed variations in call rate rather than planning in advance. We use an integrated provisioning technique which benefits from the advantages of both predictive and reactive methods. While predictive provisioning uses predicted long term call rate variations, reactive provisioning is used to correct prediction errors and handle unexpected flash traffics.

A generic Routing Protocol was proposed and evaluated in [1]. However, the various priority factors that affect call requests were not adequately modeled. A random call request pattern is an idealistic assumption. Call request patterns in reality are highly biased due to various factors- geographical context, network usage and user mobility patterns, etc. Designing an efficient routing scheme that can handle all possible random requests is a difficult task. However, the knowledge of request patterns and biasing factors can be used to handle realistic call request patterns more intelligently and efficiently.

In this paper, a load balancing scheme based on studies of call request patterns, mobility patterns, network usage patterns and other biasing factors has been proposed. The load balancing is employed by the concept of Capacity Distribution [2]. It is achieved by controlling the behavior of the routing system by dynamically allocating pair-wise channel capacity. The model learns from the temporal and geographical call distribution patterns and employs this knowledge in efficient routing. This technique is capable of controlling congestion inherently. The proposed model is simulated to evaluate the performance indicators.

The paper is organized as follows. In section II, we discuss existing approaches and some techniques investigated in literature. Section III outlines the factors that influence call request patterns. In section IV, we introduce an analytical model of a routing system and develop a provisioning algorithm. We adopt an integrated provisioning technique that combines predictive and reactive methods. The idea of Capacity Distribution is described in section V. Some implementation issues are also discussed. In section VI, we describe the simulation technique and analyze the performance of the model in terms of Call Dropping Rate, the number of calls dropped per requests. In section VII, we conclude with a short discussion on the advantages of the combined approach.

• II.    Related Work

The problems arising due to increasing traffic and hence congestion has been addressed via broadly two approaches – Call Admission Control and Load Balancing.

Call Admission Control is a preventive methodology that employs suitable decision logic to decide whether the incoming call request should be admitted or not. The sentry logic can drop a call request even if resources are available to serve the same. This is done to keep backup resources for incoming hand-off calls. Shadow Cluster Concept [5], [6] is used to allocate resources that need to be reserved for call hand-offs, and to determine if a new call should be admitted to a wireless network based on the call’s resource requirements and local traffic conditions. The framework of a shadow cluster system is completely distributed, and can be viewed as a message system where a mobile terminal informs the base stations in the neighborhood about its requirements, position, and movement parameters, so that the base stations project future demands, reserve resources accordingly, and admit only those calls that can be supported adequately. Fuzzy-based CAC schemes are used because conventional CAC must make decision based on the uncertain or inaccurate information due to the user mobility, variation of channel condition and also difficulty in obtaining the complete statistics of the network traffic.

Load balancing is a reactive methodology to distribute workload across multiple routing nodes or a cluster, in response to increased call requests to achieve optimal resource utilization and avoid overload. A cell-cluster based traffic load balancing strategy is proposed in [7]. A distributed load balancing technique in [8] uses a channel borrowing algorithm to migrate available channels to the heavily loaded ‘hot’ cells while preventing interference. A load balancing scheme for mobile networks is investigated in [9], [10] that changes cellular coverage (within the limit of the maximum coverage and capacity of the base station) according to call patterns in real time. The concept of static coverage with hexagonal network structure is removed and cell frontier is defined as the maximum outreach of its base station.

In this paper, a load balancing technique is proposed that changes the capacity between pairs of adjacent cells according to the geographic traffic distribution in real time. We combine our technique with a provisioning algorithm that supplements for high call rates thus reducing the call dropping rate and ensuring QoS.

• III.    Call Request Patterns

Call requests are never very random. They often follow trends that are influenced by several factors such as geographical context, network usage and user mobility patterns, etc. Study of network traffic traces can help characterize the call request patterns. Several researchers have already done large scale trace-driven analysis; such as in [3]. We use their observations to characterize realistic call patterns.

The following biasing factors have been identified to characterize realistic call patterns

• A.    Geographical Context

The geographical context of a locality highly affects call request patterns. If a major city is located towards North with respect to an arbitrary station or cell, it is expected to receive a major share of its call requests to and from that direction. This factor is rather intuitive and is not derived from trace analysis.

• B.    Temporal Bias

Call request patterns vary temporally. More call requests are expected to and from the industrial and commercial hubs during business hours; whereas more calls are requested towards residential suburbs during night hours. Evidently, call requests follow a well-defined temporal pattern.

• C.    Mobility and Usage

From the trace analysis in [3], we realise that local users are more active than roaming users. Also, about 66% of the users are stationary and the number of users decreases exponentially with their mobility range. 27% of the users are short-range roamers and only 6% are long-range roamers. The temporal behaviour of usage and mobility patterns is also characterized in [3].

IV.    Resource Provisioning

The provisioning algorithm attempts to allocate sufficient capacity to the cells along the route of a newly admitted call so that its QoS requirements can be met even during the peak workload. Resource provisioning approaches the problem from a queuing model perspective. Each call server or router is modelled as a Markov’s chain queue [15], [16]. The problem thus reduces to determining the maximum queue length over a specified time interval. Any provisioning problem solves for two issues: how much to provision and paper when ?

• A.    How much to provision

To compute how much additional capacity should be allocated to each cell, we construct an analytical model of a call routing system. Our analytical model computes the capacity needed at each call routing cell to handle the aggregate traffic based on two input parameters- the incoming call request rate and service demand of an individual call request.

Consider a call request is routed via a route of k cells, denoted bycvc2,.... Cit . Let the allowable end-to-end delay for the call be G , this value is specified as part of the call’s contracted QoS. The end-to-end call delay can be broken down into per-cell service times, denoted by ^ 1? ^Z^ •“ * ^ к , such that Sdi = d. Let the incoming call distribution have a peak rate of λ. Our objective is to determine how much capacity to provision for a cell such that each cell can service all incoming requests with a mean service time of for the given peak call rate.

A call routing system is modelled as a network of queues where each queue represents a routing cell (one call router/server at a cell to be precise), and the queues from a cell feed into the next cell. A generic distribution, denoted by G, is sufficiently general to capture arbitrary call arrival and service time distributions. So, we model a server at a cell as a G/G/1 queue. The G/G/1 router model allows us to break down the complex task of modelling an arbitrary routing system into more convenient units and to model each cell separately.

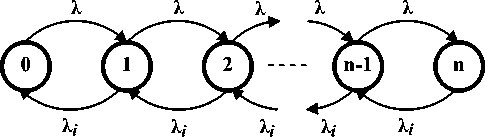
Figure 1: Call Router as a Markov’s chain queue

The following queuing theory result [15] captures the behaviour of a G/G/1 system appropriately:

X i =

" ■"

s i + W s )

- 1

where is the mean service time for cell i,   is the average service time for a request at ith cell, and is the call arrival rate to cell i. and are the variance of inter-arrival time and the variance of service time respectively. While is known, the per-cell service time as well as the variance of inter-arrival and service times and can be monitored online. Using these values in equation 1, a lower bound on request rate that can be serviced by a single server can be obtained.

After computing the capacity of a single server , the number of servers needed at cell i to service a peak request rate of λ is simply computed as:

n =

я

Л

i

The model computes the number of servers needed at the k cells to handle a peak demand of λ. We then increase the capacity of all cells to these values resulting in an immediate increase in effective capacity. If exceeds the number of available servers, excess requests must be dropped by the CAC module.

• B.    When to provision

The problem of when to provision depends on the dynamics of traffic. Call traffic exhibit long-term variations such as time-of-day or seasonal effects as well as short-term fluctuations such as flash traffic. While long-term variations can be predicted ahead of time by observing past variations, short-term fluctuations are less predictable, or in some cases, not predictable. The proposed technique adopts two different methods handling variations at different time scales. We use predictive provisioning to estimate the future workload for the next few hours and provision for it in advance. Reactive provisioning corrects errors in the long-term predictions and handles unanticipated flash traffic.

• 1)    Predictive Provisioning

The predictive provisioning is responsible for provisioning resources over long terms (time scales of hours and days). The peak traffic demand for the next several hours is predicted using a call rate predictor. Then, the model presented in Section IV (A) is used to determine the number of servers to be provisioned. Predictive provisioning is motivated by long-term patterns in call requests such as time-of-day or seasonal effects. For instance, the call rate typically peaks around noon, on working days and is least during the night hours. Similarly, the call rates boom during festivals and New Year’s Day. These cyclic patterns are repetitive in nature and can be predicted in advance by observing call rate variations in the past.

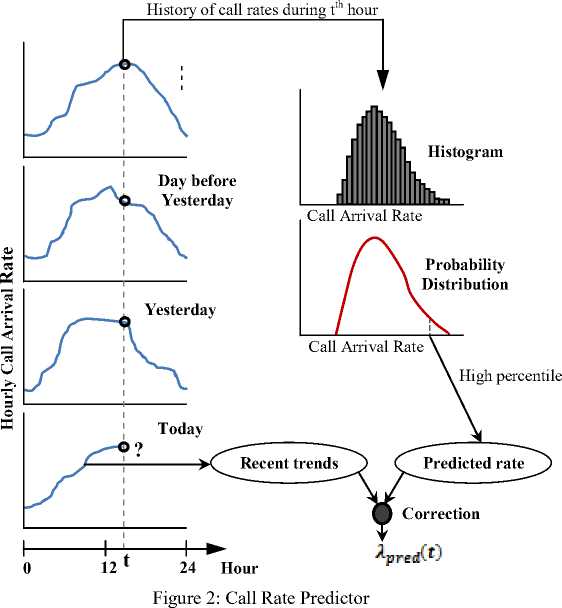
The call rate predictor uses a technique proposed in [14] that uses past records of the traffic pattern to predict peak demand that will be seen over the next hour. At the beginning of each hour, the call rate predictor estimates the peak demand over the next one hour. To do so, it keeps record of the session arrival rates for the past several days in the form of diurnal patterns. A diurnal call rate pattern may be called trendline for that particular day. The trendlines are used to generate a histogram for each hour which gives a probability distribution of the expected arrival rate for that hour. For a given hour, the peak workload during that hour is a high percentile of the arrival rate distribution for that hour (Figure 2). Other statistical predictive techniques, as proposed in [11], [12], and [13] can also be adopted for use with our techniques.

To further improve the accuracy of the call rate predictor, the call rate variations as seen in the past few hours of the current day can be used in addition to past trendlines. Let denote the predicted arrival rate for the tth hour. Also, be the actual arrival rate measured for this hour. Then, prediction error would be

. The observed prediction error can be used to correct the peak demand estimate as follows:

Apred (t) = Apred (t) + t maX(0, A” (i)) i=t - h           h where the right operand denotes the mean prediction error over the past h hours. Only the positive errors are considered to correct underestimates of the predicted peak demand; negative errors occur when the predicted worst-case call rate does not arrive in reality and is not necessarily a prediction error.

We then provision the additional capacity that should be allocated to each cell in advance using the predicted peak call rates. Thus predictive provisioning technique attempts to stay ahead of the anticipated variations in traffic demand.

• 2)    Reactive Provisioning

The call rate predictor is not always accurate—it may incur errors if the actual call arrival pattern on a day differs heavily from its observed behaviour in the past. Furthermore, sudden flash traffics are inherently unpredictable. Reactive provisioning swiftly reacts to such unanticipated events. Reactive provisioning operates on a shorter time scale—on the order of minutes— checking for deviations from predicted arrival rates. If any fluctuations are detected, additional capacity is allocated to various cells to handle the call rate increase.

Reactive provisioning is invoked periodically once every few minutes. The currently observed call arrival rate over the past few minutes is compared with the predicted rate         . If their difference exceeds a pre-set threshold value, i.e

A obs ( t ) _ > ^T A pred ( t )     ¹

then a new capacity allocation is computed using the observed arrival rate .

Also, it can be invoked on-demand when the observed call dropping rate (CDR) increases beyond a threshold, i.e.

CDR > т 2

In either case corrective action is invoked by recomputing the capacity allocation. Thus reactive provisioning follows actual call rate fluctuations correcting for errors and unanticipated fluctuations.

V.    Capacity Distribution

The essential idea behind Capacity Distribution is to suitably allocate Capacity between pairs of adjacent stations or cells and thus enforce priority over routing. Previously in [1], Capacity had been defined for a particular Base Station. The model is extended by defining Capacity between a pair of two adjacent stations. While provisioning supplements additional capacity required to serve the peak call rate, Capacity Distribution assumes a constant cell capacity and distributes this capacity heterogeneously among adjacent cell pairs according to the geographic call distribution in real time. This allows us to handle calls more intelligently and implement priority based routing.

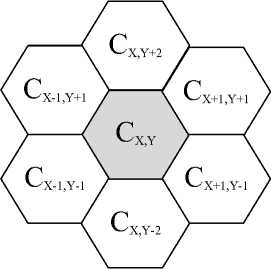
Figure 3: A Cellular Unit

A Cellular Unit for the cell C X,Y is its union with its six adjacent cells, as shown in Figure 3. Each cell forms such a Cellular Unit and has six Capacity and Congestion values, one associated with each adjacent cell of its Cellular Unit.

Capacities- ς(0,2)   Congestions- χ(0,2) ς(1,1) χ(1,1) ς(1,-1) χ(1,-1) ς(0,-2) χ(0,-2) ς(-1,-1) χ(-1,-1) ς(-1,1) χ(-1,1) where ς(a,b) is the capacity between Cx,y and Cx+a,y+b ; χ(a,b) is the congestion between Cx,y and Cx+a,y+b ; a ϵ {-1, 0, 1} ; b ϵ { -2, -1, 1, 2} ; |a| + |b| = 2.

• A.    Determining Capacity Values

A Cellular Unit can be tuned to handle call requests by Priority based Routing by suitably adjusting the values for the six pair-wise capacities ς. Some Priority based Routing models are discussed in [4].

• 1)    Initialize by Geographical Context:

Suppose that a busy city is situated eastward to a particular cell. Obviously, the cell will receive more requests to and from this direction. This Geographical Context factor determines the initial capacity distribution. So, to implement this priority, ς(1,1) and ς(1,-1) will have higher values than the rest. The initial capacity distribution is computed only once.

• 2)    Periodic update by Network Usage Statistics

The capacity distribution needs to be updated to adapt dynamically to the continuously changing traffic patterns. A weighted sum of the congestion values over a period of time is added to the existing capacity distribution to obtain the new distribution. The following update policies are proposed.

• a)    Periodic Proportional Sharing: The cell pairs share the total Capacity C proportional to the congestion between cell pairs over a specific time interval τ. τ is called the Update Interval .

x ( a , b )

f (a , b )    = C x--------

, new

1 x ( a, b )

• b)    Periodic Retentive Sharing: This is similar to the above update policy. Additionally, a part of the initial capacity distribution is retained.

f ⁽ a , ^Ь) new = P ^X f ⁽ a , ^Ь) + ⁽¹ - P )

C _x x ⁽ a , b ) 1 x ( a, b )

The fraction ρ of initial capacity value that is retained is termed Retentivity and 0 < ρ < 1.

• B.    Blocking and Borrowing

Capacity Distribution essentially allocates a Capacity value between a pair of adjacent cells. Consequently, whenever the Capacity between two adjacent participating cells is full, further call requests are blocked even though the total capacities of both are not fully used. This results in underutilization of the channel capacity. We term this situation as Blocking.

One simple solution to prevent Blocking is Borrowing. When a call request gets blocked, a unit Capacity may be borrowed from the most underutilized cell pair in order to serve the new request. However, this borrowed capacity must be returned as soon as the call is ended to maintain the actual capacity distribution. Unrestricted Borrowing can also distort the capacity distribution temporarily. So, Borrowing must be a limited to an extent. The better solution is to allow borrowing a limited part of one’s Capacity in order to serve blocked call requests; this is termed as Restricted Borrowing. Let β be the fraction of total cell capacity that can be borrowed. To restrict borrowing, we keep a counter that is incremented upon each capacity borrowing and decremented when the call is ended. A call request must be dropped if while attempting to borrow capacity from a cell pair, the counter value exceeds borrowable capacity, i.e counter > в x C where is the total cell capacity. Once a call is dropped, the Reactive provisioning method must be invoked on-demand to attempt provisioning additional routers. Experiments suggest that the borrowing fraction β of a cell be assigned values in the range [0.1, 0.5] to avoid temporary shifts in the capacity distribution. β can further vary dynamically in response to increased call dropping rate.

Algorithm 1 is an extended version of the Directed Call Routing algorithm in [1]. ∂ is the distance as defined in [1]. The storage and distribution of capacity values as well as the concept of borrowing has been reflected on the algorithm. The borrow(a,b) method finds the most underutilized cell pair (x,y). If , the method returns no lender, otherwise it borrows an unit capacity from (x,y) to (a,b) and returns (x,y) as the lender.

ALGORITHM I: Capacity Distributed Routing

Input :    Source C sx,sy , Destination C dx,dy

Output : Priority based routing path.

Method :

capacity_distributed_routing(C x,y )

d=∂(C x,y ,C dx,dy )

for each cell Cx+a y+b in Cellular Unit of Cxy if (∂(Cx+a,y+b,C, dx,dy) ≤ d)                  , if (b > 0)

if (ς(a,b) x,y = χ(a,b) x,y )

if ((lender=borrow(a,b))=NULL) drop_call( )

end if end if capacity_distributed_routing(Cx+a,y+b) end_call( )

if (lender ≠ NULL) ς(a,b) x,y --ς(lender) x,y ++ end if else if (ς(-a,-b) x+a,y+b = χ(-a,-b) x+a,y+b)

if ((lender=borrow(-a,-b)) = NULL) drop_call( )

end if end if capacity_distributed_routing(Cx+a,y+b) end_call( )

if (lender ≠ NULL) ς(a,b) x+a,y+b --ς(lender) x+a,y+b ++ end if end if end if end loop

}

• C.    Congestion Control

By Capacity Distribution, we dynamically allocate more capacity between those cell pairs which are expected to serve more requests or are observed to be more active in call forwarding. Thereby, lesser number of frequent short duration calls between high priority cell pairs get blocked by long duration calls between low priority cell pairs. This reduces the Call Dropping Rate.

The number of call drops is lesser as the model is more adaptive to the continuous changes in traffic and usage patterns. Hence, the model controls congestion inherently. By properly setting the update interval τ, retentivity ρ or even by employing better heuristic update policies, better congestion control can be achieved.

VI.    Simulation Results

The model is simulated by programming the behaviour functions of a small field of cells and then forwarding various call request patterns over it. Call requests are routed across a K×K cellular field using the Coordinate based Directed Routing Protocol in [1]. Realistic conditions are simulated by configuring the various parameters like field size, call request rates, call durations, geographical priority, capacity, update interval, retentivity, etc.

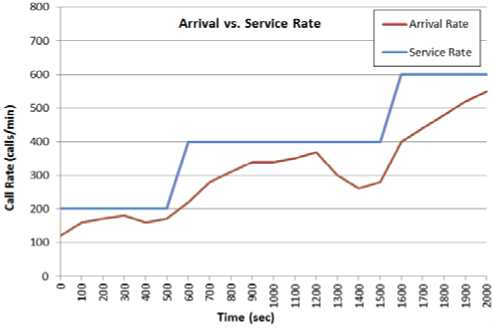
Figure 4: Call Arrival vs. Service Rate

The effect of dynamic provisioning is evident in Figure 4. The service rate curve stays ahead of the arrival rate curve until additional servers are available for provisioning.

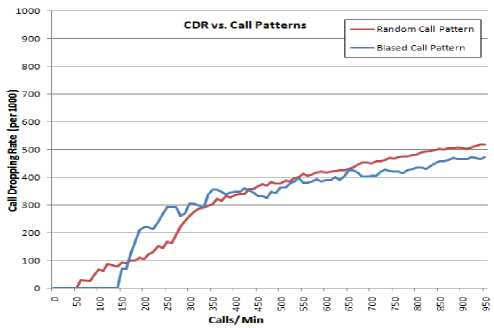
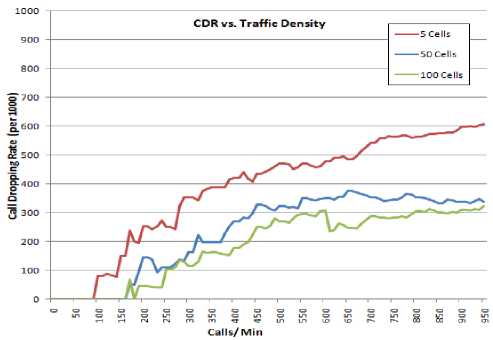
Figure 5 (b)

Figure 5: CDR vs. Traffic (a) Call Patterns (b) Traffic Density

The performance of the model is evaluated in terms of Call Dropping Rate (CDR). The plots in Figure 5(a) are actually aggregated values of several call request patterns. Evidently, the Capacity Distribution model handles the biased call request patterns more efficiently. After the full capacity point (C=100), the CDR for biased call patterns rises steeply but tends to saturate faster than the random call patterns. The simulation of the same traffic over various sizes of field is shown in Figure 5(b). As expected, the CDR is higher in a field with denser traffic.

The adaptability of the model is assessed by varying the capacity updation policies with different update intervals (τ) and retentivities (ρ). The effect of varying these two parameters is observed to be dependent on the call request rates and call patterns as well. As evident in Figure 6(a), decreasing the update interval τ decreases the CDR in general. This means that the Capacity Distribution model adapts quickly to the changing traffic and usage patterns. However, the best CDR is achieved at intermediate values of τ for higher call request rates. So, longer update intervals are required for properly adapting to the frequent changes in a high call request rate. As seen in Figure 6 (b), the variation of CDR with retentivity ρ is rather erratic in nature. Remarkably low CDR values are attained at particular values of ρ. Optimal adaption to a call request pattern thus requires a suitable combination of both τ and ρ.

Figure 5 (a)

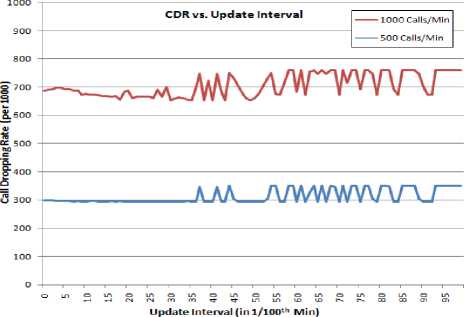
Figure 6(a)

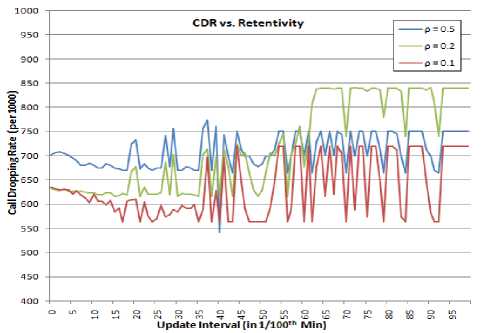
Figure 6(b)

Figure 6: CDR vs. Adaptability (a) Update Interval (b) Retentivity

VII.    Conclusions

We unite provisioning and load balancing techniques for call routing in mobile networks. Our analytical model of a call routing system is able to model a complex network into a network of queues. We develop a provisioning algorithm using this model. Our integrated provisioning technique provides additional resources for predicted and observed temporal variations in call patterns. The predictive provisioning attempts to predict long term call rate variations and adapt accordingly. The reactive provisioning, which is scheduled on a much smaller time scale, compensates for prediction errors and handles flash traffics.

Capacity Distribution is a new dynamic approach towards load balancing. We identified some key biasing factors that characterize realistic call patterns and accordingly selected the priority factors. Since it responds to varying call request patterns, proper tuning and selection of update policy is required for optimal performance. The model achieves better performance in terms of CDR while maintaining simplicity and adaptability. Moreover, the model also has inherent congestion control ability.