Restoration of Degraded Gray Images Using Genetic Algorithm

• I.    Introduction

  Image deblurring and Image Restoration [1][2][3][4][5] is quite useful application of Digital Image Processing [6][7][8] and has began in 1950s with the space program [9][10]. Image deblurring has been a very popular topic due to its wide variety of applications. Image deblurring is concerned with filtering of the observed image to minimize the effect of degradations. Image deblurring depends on the accuracy of the knowledge of the degradation process, which is a mathematical model of blurring process. Design of deblurring filters depends on this knowledge. The objective of image restoration is to recover an image which is degraded by electronic or optical process, the process may be relative motion between the camera and original scene or camera misfocus, atmospheric turbulence, or some distortion occurred due to sensors.

• A. Degradation Model

Image degradation model is very important in image restoration process. Once degradation model is known one can get restored image by applying some restoration or filtration process. Graphically, Image Degradation model may be visualized as:

Let an image f(x,y) a 2D function, is degraded by some degradation function H , Degradation Process represents the Image Degradation Model [11,12] :

Noise

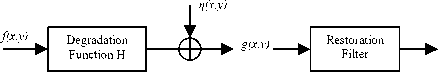
Degradation Process

Restoration Process

Fig.1. Image Degradation Model

From the above model, we may build up a linear relationship and modeled degradation process as a convolution process (in spatial domain) as:

g ( x , y ) = h ( x , y ) * f ( x , y ) + n ( x, y)    (1)

Or can be expressed as:

g(x, y) = H[f (x, y)] + n( x, y)

where (x,y) is discrete pixel coordinate of the image and ‘*’ is a 2D convolution,

f(x,y) is an Original Image

g(x,y) is an Degraded/blurred Image

h(x,y) is point spread function(PSF)

n(x,y) is some kind of noise.

f'(x,y) is an Restored Image (estimate of f(x,y) computed from g(x,y) ).

Since Convolution in spatial domain is equal to the multiplication in frequency domain; Therefore, In Fourier domain(frequency domain), the corresponding operation may be represented as:

G(u,v) = H(u, v)F(u, v) + N(u, v)       (2)

Where H(u,v), F(u,v) and N(u,v) are the Fourier Transforms of h(x,y), f(x,y) and n(x,y) respectively. Here H is degradation operator which is applied on input image.

If the system contains no noise we may assume n ( x,y ) = 0 and g ( x,y ) = H [ f ( x,y )] (from eq. 1) . For the linear spatial model depicted in Fig.1, we may also write

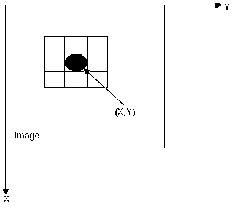
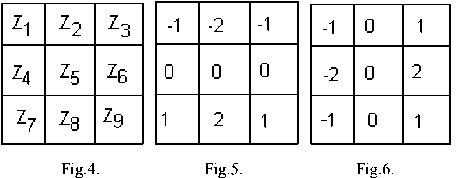
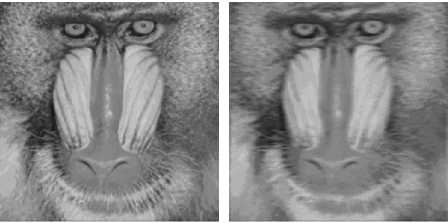
S[^(xy)+^(xy)]=^^(xy)}^S[j£

aid

z£^(xy)]=^ff[X(xyO

Both above equations say that the response to the sum of many inputs equals the sum of the response to each individual input. This is known as the additivity property and other equation indicates that the response to a constant multiple of any input is equal to the response to that input multiplied by the particular constant. This is referred to as the homogeneity property. The operator H is said to be position or space invariant if

H(x-α,y-β) = g(x-α,y-β)

for any f(x,y) and any variables α and β.

Fig.2 shows the blurred image can be restored by using some restoration process.

Fig.2.

The most important component in degradation model is the PSF, which is equivalent to the impulse response of a 2D system and describes the distortion imposed by an optical system. If f (u, v) is a two-dimensional function describing the object of interest, then its image, g(x, y), can be stated as

∞ g(x, y) = ∫

-∞

∞

,v,x, y) f (u, v)dudv

-∞

where (u, v) and (x, y) represent the spatial coordinates of the object and image, respectively, and h(u, v, x, y) is the PSF of the system producing the image g(x, y).

For the purpose of objectively testing the performance of image restoration algorithms, we used three statistical measures i.e., improvement in signal to noise ratio(ISNR), Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR). The Improvement in signal to noise ratio(ISNR) may be defined as the improvement in the quality of the estimated image over the blurred image [33]

ISNR = g-f²f -f'²

Where f, g and f' represents original image, blurred image and restored image respectively. Higher values of ISNR signify good results and lower values of ISNR represent poor results. Mean Square Error(MSE) is a quality measures which quantitatively recognize the strength of error signal. MSE is commonly used because it has a simple mathematical structure and easy to implement. If f(x,y) be a input image and its desired or restored image is f’(x,y) then, Mean Square Error may be defined as :

MN

MSE=(1/MN)(∑∑(f(x,y)-f'(x,y))²)⁽⁸⁾

x=1 y=1

and Peak to Signal Noise Ratio (PSNR), defined as :

PSNR=10*log(255)²/MSE       (9)

Where f(x,y) is original image, f'(x,y) is restored image and M, N is size of image.

Image restoration involves finding the restored image from the degraded image such that value of Mean Square Error is minimum, means; higher value of Mean Square Error (MSE) refers to the poor quality of image and the lower value of the MSE represent good quality of the image.

• II.    Restoration Approaches

The process of image restoration may be categorized in two main classes ; if the degradation process [13][14][15] or point spread function (PSF) is exactly known, then the restoration can be done using deconvolution; and if there is no information about point spread function [16][17], then it is known as blind deconvolution. When the intensity of observed point image spread out over several pixels, this is known as Point Spread Function (PSF)[18]. The high-quality achievement of restoration process depends on PSF. The PSF is categorized by two parameters i.e. blur length and blur angle. Blur length is number of pixels by which the image has been degraded; means number of pixel positions shifted from one place to another place. Blur angle is the angle at which the image has been corrupted.

There is a dense literature on Image Restoration [19][20][21] techniques in which most common techniques are the inverse filter, the Wienier filter, the average filter, the mean square error filter, Richardson-Lucy algorithm [22][23] and Regularization filter. Inverse filter was designed by Nathan in 1966 for the restoration of images. It is a very simple filter for restoration. In inverse filter restoration technique, blur function is known and if noise is not present, this technique produces good restoration results. It is very sensitive to additive noise; means in presence of noise inverse filter is not able to produce good results. On the other hand, Wiener filter removes the additive noise and provide better restoration results than inverse filtering and regularizing filter. The Richardson-Lucy method (Richardson 1972, Lucy 1974) was developed specifically for data comprising discrete, countable events that follow a Poisson distribution. W. Dong [34] proposed an advanced image restoration method by introducing two adaptive regularization terms into the sparse representation framework. First, a set of autoregressive (AR) models are learned from the dataset of example image patches. The best fitted AR models to a given patch are adaptively selected to regularize the local structures of image. Second, the image non-local selfsimilarity is introduced as another regularization term. In addition, the sparsity regularization parameter in      W.

Dong method [34] is adaptively estimated for better image restoration performance.

• III.    Proposed Algorithm Description: Image Restoration Model

We proposed following algorithm for image restoration using genetic algorithm:

Step 1 : Get Blurred Image (initial image)

Step 2 : Apply Fast Fourier Transform on blurred Image

Step 3 : Apply Inverse Fourier Transform and create an initial population for applying Genetic Algorithm.

Step 4 : Calculate the value of objective functions for the current population

Step 5 : Apply cumulative fitness assignment criteria and selection procedure Use Genetic Algorithm for selection of new population.

Step 6 : Find best individuals

Step 7: Apply Crossover and Mutation on the new population (obtained at Step 5) for creating a new population.

Step 8 : Get restored image using best individuals (obtained at Step 6).

We used Genetic Algorithm to produce better results. In Genetic Algorithm, at each iteration, a new set of approximation is created by the process of selecting individuals according to their level of fitness in the problem domain and breeding them together using operators borrowed from natural genetics. This process leads to the evolution of population of individuals that are better suited to the environment than the individuals from which they are created, as in natural adaptation. The members in the population having high fitness values are called most fit members, only can survive, and the least fit members (having low fitness value) are eliminated from the population.

We proposed Image Restoration method which is similar to local transformation [24] that is based on gray level distribution in the neighborhood of every pixel is given as

g(x, y) =k*{M/(σ(x, y)+b}*{f(x, y) -c*m(x, y)}+m(x, y)a

(4) where g (x,y) stands for output pixel intensities f (x,y) stands for input pixel intensities

M stands for the global mean

σ (x,y) and m (x,y) stands for the local standard deviation and mean calculated in the neighborhood of 3x3

a.b.c and k are tunable parameters

A 3x3 neighborhood around a point (x,y) in an image is shown below –

Fig.3. A 3x3 neighborhood about a point (x,y) in an image[6]

For Image restoration we have considered three objectives, namely intensity, entropy and number of edges. The proposed method tries to maximize all the objectives. We have proposed a fitness function criteria which is based on individual objective i.e. intensity, entropy and edges. After evaluating fitness of all individual objectives (Entropy, Edge and Intensity); combined fitness or cumulative fitness is calculated. Our method evaluates all the objectives and maximizes them; means Image restoration criteria may be defined as a function of entropy, edges and Intensity.

Edges in an image can be defined as rapid changes in image intensity over a small region. One method of measuring these changes is to use discrete difference operators. It consists of two masks which calculate the change in both the directions i.e. in the x-direction and y-direction respectively.

Fig.4 shows a 3x3 region of Image, Z’s are gray level values and masks are used to compute gradient at point Z₅. In Fig.5 Sobel mask for gradient component Gx and in Fig.6 Sobel mask for gradient component Gy are represented.

For image pixel I(x,y) labeled as Z₅ above

G_x = (Z₇ + 2*Z₈ + Z„) - (Z, + 2*Z₂ + Z₃)

Gy = (Z3 + 2*Z₆ + ZJ - Z + 2*Z₄ + Z7)

and

Gradiant = [G² + G²]¹'²

xy

In Genetic Algorithm, we use genetic operators like Selection, Crossover and Mutation Operators. Genetic Operators are the steps that guide the Genetic Algorithm towards better solutions. In Genetic Algorithm, search space or state space; act as a container of all the feasible (possibly best) solutions. Each point in the search space represents one possible solution, marked by its value which is called its fitness value.

To formulate the process of natural solution in a machine, a method is needed to encode potential solution of the problem in the form that a computer can process, is known as representation technique. Chromosome of image are to be represented as an array of real integer of length four [a, k, b, c] where a, k, b and c are the parameter and the values of a ranging from 0 to 1.5, k from 0.5 to 1, b from 0 to 0.5 and c from 0 to 1.0. We applied Tournament selection which operates by choosing some individuals randomly from a population and selecting the best from this group to survive in the next generation. Once Selection has chosen fit individuals, they must be randomly altered with the hope of improving their fitness for the next generation. Crossover is a mating technique to produce better individuals. In Crossover, two individuals are chosen to swap segments of their code, to produce offspring. We have used Arithmetic Crossover [26]. Arithmetic Crossover can be defined as a linear combination of two chromosomes as :

Offspring 1 = p*a + (1-p)* в

Offspring 2 = (1 - p)* a + p * в

Where α and β be two parents in the mating pool and p is a random number and p e [0,1] .

We have taken different images of same sizes. Maximum number of generation to run the program is chosen as 20; this also works as the criteria to stop the evolution. Mutation has to be taken as simple mutation having probability = 0.1, Arithmetic crossover has to be taken having crossover probability = 0.8, selection has been taken as tournament selection, and finally, size of the population has to be taken as 48.

In the proposed method we have used Genetic Algorithm with three objective parameters; number of edge points to identify the clear boundary, intensity for enhancement and improvement in image quality and particularly third parameter, which plays an important role in image restoration, is entropy because it is a measure of disorders in the image. It restores undistorted frequency content using iterative process with help of genetic algorithm. The randomness of noise leads to higher entropy, whereas an undistorted image possesses smaller entropy. Since entropy is very useful in subjective identification of the image quality therefore we have used it as information parameter [27][28]. A number of research has support our claim [29][30][31][32].

• IV.    Experimental Results

We have developed computer programs for our proposed method and other methods on the Computer System having Microsoft Windows XP Professional Service Pack 3 operating system, Intel Pentium 3.20GHz processor with 512 MB Ram, and using MATLAB 7.0 (R14) software. We have illustrated the proposed image restoration technique on various gray level images of same sizes. The framework that we proposed here addresses a new restoration criteria using genetic algorithm. For evaluating the accuracy of our proposed method, we have tested the proposed method on various statistical measures which minimizes the restoration error and maximize the image quality. The original image is degraded by motion blur having length=7 pixels and angle=0 degree. On the basis of the image quality and quantitative performance measures, we have compared our proposed method with three other Image Restoration methods namely Lucy-Richardson method, W. Dong Image Restoration Method [34] and Inverse Filter Method.

We have taken five images namely Peppers, House, Baboon, Barbara and cameraman of same sizes having 256x256 pixels. All these images are gray scales images. We have degraded these images using motion blur having length =7 pixels and angle =0 degrees. We have restored the blurred images by the proposed method and other method. Performance of the methods were compared on the basis of values of different quantitative performance measures i.e. Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR) and Improvement in Signal to Noise Ratio (ISNR). The values of these measures for different methods are shown in Table 1 to Table 3. The restoration results using the proposed method and other methods are visually shown in Fig.7 to Fig.11.

Fig.7. Restoration results on ‘peppers’ image : (a) original image, (b) blurred image, (c) Restored image by W. Dong method [34], (d) Restored image by Lucy-Richardson method, (e) Restored image by Inverse filter method, (f) Restored image by the proposed method.

(фВИК-1 1473              (в) BUR--33734              (f) ISNR-4 6172

Fig.8. Restoration results on house image: (a) original image, (b) blurred image, (c) Restored image by W. Dong method [34], (d) Restored image by Lucy-Richardson method, (e) Restored image by Inverse filter method, (f) Restored image by the proposed method.

(ttllSHR-0.6048 dB            (e)ISNR--4.9884 dB             (fl ISNR-3.2917 dB

Fig.11. Restoration results on cameraman image : (a) original image, (b) blurred image, (c) Restored image by W. Dong method [34], (d) Restored image by Lucy-Richardson method, (e) Restored image by Inverse filter method, (f) Restored image by the proposed method.

Fig.9. Restoration results on baboon image : (a) original image, (b) blurred image, (c) Restored image by W. Dong method [34], (d) Restored image by Lucy-Richardson method, (e) Restored image by Inverse filter method, (f) Restored image by the proposed method.

In Table 1, MSE values for restored images by different images are shown. MSE values in the results obtained by the proposed method are less than result obtained by Lucy-Richardson method and inverse filter method both.

Table 1. MSE value of Images Using different methods

Fig.10. Restoration results on barbara image: (a) original image, (b) blurred image, (c) Restored image by W. Dong method [34], (d) Restored image by Lucy-Richardson method, (e) Restored image by Inverse filter method, (f) Restored image by the proposed method

In Table 2, the values of Peak Signal for the restored images by proposed method and other methods are shown. PSNR values in the results obtained by the proposed method are higher than results obtained by Lucy-Richardson method, W. Dong method and inverse filter method; the results obtained by the proposed method are btter in terms of Peak Signal to Noise Ratio.

Table 2. PSNR value of Images Using different methods

Finally; in Table 3, we have given the Improvement in Signal to Noise ratio (ISNR) values for the restored images by the proposed method and other methods. Higher values of ISNR represent good results and in the proposed method, each ISNR value is higher than values obtained by application of Lucy-Richardson method, W. Dong Method and inverse filter method. So the proposed method performs better in terms of Improvement in signal to noise ratio (ISNR).

Table 3. ISNR value of Images Using different methods

By comparing the visibility details of restored images, we can find that all the restored images generated through the proposed method have no blur or ringing effect across the boundaries and around the edges of the image. We can also observe that by applying Lucy-Richardson restoration method, the high and low intensity areas of the image are equally restored. Our proposed method restores the low as well as high intensity areas of the image and it also enhances the image property. Therefore, we can conclude that proposed method perform better for image restoration. By comparison with results obtained by Lucy-Richardson method, W. Dong method and inverse filter method, we can find that our proposed method deblur the images in better way.

Again, we have also tested the proposed method in the presence of Blur and Gaussian noise both, means now distorted image is blurred as well as noisy and it is to be restored by using our proposed method and compared with restoration results of Lucy-Richardson, W. Dong Method and Inverse Filter restoration method. We have generated the blurred and noisy images by taking blur length=7 and zero mean Gaussian noise with variance=.0001 as shown in Fig.12.

(a)                              (b)

Table 5. PSNR value of Images Using different methods

(c)

(d)

Fig.12. (a) original baboon image, (b) blurred and corrupted by Gaussian noise baboon image having noise variance=.0001, (c) original cameraman image and (d) blurred and corrupted by Gaussian noise cameraman image having noise variance=.0001

(a) ISNR = 0.2951 dB (b) ISNR = -4.6054 dB (c) ISNR = 3.6377 dB

Fig.13. Restored image by (a) Lucy-Richardson restoration method, (b) Inverse filter restored image and (c) the proposed method.

(a) ISNR = 1.2364 dB (b) ISNR

= -3.5130 dB (c) ISNR = 6.9041 dB

Fig.14. Restored image by (a) Lucy-Richardson restoration method, (b) Inverse filter restored image and (c) the proposed method.

Table 4. MSE value of Images Using different methods

Table 6. ISNR value of Images Using different methods

In Table 4 to Table 6 we have given MSE, PSNR and ISNR values of restored image obtained by the proposed method and Lucy-Richardson method, W. Dong method and Inverse filter method. These values suggest that the proposed method shows good results. As the result shown above, in the presence of noise, Inverse filtration method is not well suited for image restoration where as Lucy-Richardson method is good for image restoration in presence of noise. We have also visually compared and shown the results in Fig. 13 and Fig. 14, and therefore we can conclude that in presence of noise the proposed method provide good restoration results.

• V.    Conclusions

This paper examines and identified the gray images which have been distorted by some way and recovered their features by restoration process using Genetic Algorithm. In this paper, we have developed a strategy for restoration of blurred gray images. It has been found that the proposed method is and given improved results of image restoration and it can also be seen that by using the proposed method, very promising and excellent results are achieved. All the results are visually shown in various figures qualitatively and in tables quantitatively. We believe that our proposed method definitely bring a massive impact in the research towards digital image processing. Further, the proposed method may also be extended by applying on other image processing applications [35][36] that falls under the research areas like medical imaging to find remarkable results.