Ретуширование и восстановление отсутствующих частей изображений с помощью итерационного вычисления их спектров

Практически любая область деятельности современного человека немыслима без применения компьютерных технологий. Особое развитие получили методы цифровой обработки изображений, которые широко применяются в медицине, аэрокосмическом мониторинге, при реставрации предметов изобразительного искусства, в обеспечении безопасности и других областях человеческой деятельности.

Одной из задач цифровой обработки является заполнение или восстановление отсутствующих частей изображения (лакун). Появление лакун может быть обусловлено сознательным изъятием части изображения. В этом случае целью заполнения лакуны является скрытие факта изъятия. Для этой цели привлекают соответствующие средства – методы image inpainting, в том числе нейронные сети [1, 2]. Image inpainting заполняет (буквально зарисовывает) лакуны вероятностным способом так, чтобы это казалось естественным человеческому глазу. Методы image inpainting, кроме удаления нежелательных объектов с изображения, часто используются при виртуальной реставрации старых фотоснимков и предметов изобразительного искусства (ретуширование недостающих пикселей и повреждённых областей так, чтобы это выглядело правдоподобным). Все манипуляции при таком подходе происходят в пространственной области. Для заполнения лакун выбираются наиболее похожие блоки (фрагменты). В качестве баз данных (библиотек) используется либо само исходное изображение (его неповреждённые области), либо набор подобных по структуре эталонных изображений (обучающая выборка). Основная проблема image inpainting связана с тем, что при значительных размерах лакун большинство алгоритмов не могут поддер- живать непрерывность структуры и согласованность текстур для получения визуально правдоподобных результатов после реконструкции.

Лакуны на изображении могут образоваться при затенении расфокусированных или смазанных интересующих нас объектов [3, 4]. Восстановление информации о затенённых объектах возможно при некоторых условиях. В эти условия входит не только информация о виде искажения (расфокус или смаз), но и условие соотношения размера лакуны по отношению к величине расфокуса или смаза [3, 4]. Если известно, какой объект должен быть на месте лакуны, то целью заполнения лакуны может быть выяснение ориентации, размера и количества этих объектов. При такой постановке задачи после реконструкции содержимого лакун ко всему изображению применяют известные методы деконволюции. В этом и некоторых других случаях при заполнении лакун эффективна интерполяция – линейная, весовая или сплайновая. Как правило, интерполяцию изображения целесообразно применять при малом поперечном размере лакун (в том числе разреженные изображения).

В аэрокосмических изображениях из-за технических особенностей аппаратуры и методик измерений (специфики траекторий) в пространственно-временной структуре спутниковых данных зачастую возникают лакуны (незаполненные данными области). Кроме этого, при регистрации изображений в оптическом диапазоне есть вероятность того, что изображение может быть частично закрыто облаками. Поэтому восстановление данных для подобных лакун является важным и актуальным. Для построения по спутниковым данным карт рельефа местности, по массиву ра-диояркостных температур карт восстанавливаемых атмосферных параметров обычно применяют различ- ные интерполяционные модели. Например, в [5, 6] подобные задачи решают на основе вариационного алгоритма фильтрации линейных систем уравнений.

В случае медленно меняющейся яркости на изображениях, автокорреляционная функция которых шире, чем размер лакун, заполнение отсутствующих областей изображения возможно, как уже было сказано выше, каким-либо из методов интерполяции. Но в случае достаточно контрастных изображений проблема достоверности реконструкции содержимого лакун очень актуальна. Поэтому, если есть такая возможность, лакуны одной базы данных обычно дополняются из другой базы данных, как, например, при геоинформационном картографировании Фобоса по результатам обработки данных дистанционного зондирования космического аппарата Mars Express [7]. В [8] представлены методики пространственно-временной интерполяции лакун, которые предусматривают взаимное дополнение всех доступных данных с функционирующих космических аппаратов. В результате получаются два глобальных радиотепловых поля в сутки, пригодных для изучения процессов системы «океан – атмосфера» и их пространственновременных неоднородностей в широком диапазоне масштабов. Развитием этого направления является разработка мультисенсорного алгоритма спутникового радиотепловидения, позволяющего объединить данные спутникового радиотеплового мониторинга Земли из разных источников в рамках единой схемы пространственно-временной интерполяции, учитывающей различия во времени и пространственном разрешении съёмки разными приборами [9]. Авторы этого алгоритма констатируют: «Построение опорных полей наталкивается на ряд трудностей, связанных с ограниченным объёмом доступной спутниковой информации. В частности, применяемый алгоритм «сшивки лакун» не гарантирует восстановление значений геофизического параметра во всех узлах пропуска данных с какой-либо наперёд заданной точностью, а направлен на минимизацию возмущений конечного интерполяционного решения вследствие краевых эффектов на границах полос сканирования» [9].

В данной работе мы рассматриваем тот случай, когда нет другой информации о содержимом утраченной части изображения, кроме оставшейся части изображения. Одним из вариантов решения такой задачи может быть использование спектра изображения. Следует учесть, что интерполяцию Котельникова [10], которая справедлива для сигналов с ограниченным спектром, использовать нельзя из-за большого цифрового шума. Поэтому нами предлагается применить метод интерполяции последовательно вычисляемого спектра Фурье (МИПВС) [11, 12], позволяющий ретушировать и восстанавливать отсутствующие (затенённые) части изображения. В отличие от некоторых традиционных методов интерполяций МИПВС можно использовать при любой форме отсутствующей части изображения. Ретуширование и восстановление МИПВС изображения может дать хорошие ре- зультаты даже при значительной доле отсутствующего изображения. Предложенная нами методика не требует никакой априорной информации о том, каким было реконструируемое изображение до повреждения. Информация берётся непосредственно из исходного спектра повреждённого объекта. Заполнение отсутствующей части изображения делается итерационно (от нулевой пространственной частоты до наивысшей пространственной частоты) на основе спектра присутствующей части изображения.

В этой работе для сравнения с предлагаемым нами методом лакуны заполняются с помощью сплайн-интерполяции, описанной в [13, 14]. Физический смысл этого метода заключается в том, что для произвольного набора опорных точек (узлов) решается система линейных уравнений, моделирующая поведение изогнутой упругой пластинки. В результате получается соотношение, описывающее двумерную сплайн-поверхность. Причём есть возможность учитывать при вычислении сплайна кайму вокруг лакуны шириной от одного до нескольких ближайших пикселов. Такой подход обладает определённой универсальностью и может быть применим для сравнительного анализа с методом интерполяции последовательно вычисляемого спектра Фурье. Сравнение МИПВС с более простыми способами интерполяции, например, линейной, будет не вполне корректным. Потому что при произвольных формах лакун, их расположении и ориентации необходимы априорные знания о местах и направлениях линий интерполяции. Кроме того, для сравнения с предложенным нами методом МИПВС выбрана реализация подхода image inpainting, созданная известной российской компанией Movavi, использующая для своей работы нейросеть [20].

Существуют ещё и другие методы обработки изображений, в том числе с помощью фракталов, но в нашем исследовании они не обсуждаются.

Целью данной работы является сравнение результатов заполнения разными методами лакун на изображении. В качестве базовых изображений рассматриваются поле интегрального паросодержания атмосферы и тестовые изображения.

Описание алгоритма метода интерполяции последовательно вычисляемого спектра Фурье

Идеология МИПВС кратко может быть представлена следующим образом. Полное изображение Yp можно записать как сумму изображений вне лакуны Y –L и внутри неё Y L :

Yp = Y - l + Y l .                                     (1)

Пусть маска, с помощью которой можно из полного изображения получить изображение с лакуной, обозначена как L , и эта маска внутри лакуны равна 1, а вне лакуны равна нулю.

Тогда выражение (1) можно записать так:

Yp = Y - l + LYp .                                (2)

Под спектром изображения понимается Фурье-образ этого изображения, полученный в результате выполнения дискретного преобразования Фурье. Найдём спектр (2) и получим

( δ- fL )* fYp = fL - L ,                             (3)

где δ – дельта-функция, fL – спектр маски L для получения лакуны; fYp – спектр полного изображения; fY –L – спектр изображения с лакуной, знак (*) обозначает операцию свёртки.

Решение (3) можно производить итерационно.

Таким образом, работа МИПВС происходит следующим образом:

• 1.    Локализуем лакуну, т.е. определяем координаты всех пикселей изображения, которые необходимо заполнить с помощью МИПВС.

• 2.    Устанавливаем частоту ограничения спектра F = 0. В этом случае значение амплитуды спектра соответствует средней яркости изображения (без пикселей из лакуны).

• 3.    Заполняем лакуну значениями яркости, вычисленными в предыдущем пункте, то есть получаем первое приближение заполнения лакуны. При этом неискажённая часть изображения (изначально достоверно известная) не подвергается никаким изменениям.

• 4.    Вычисляем полный пространственный спектр изображения, полученного при выполнении предыдущего пункта (с заполненной лакуной).

• 5.    Увеличиваем F на единицу. Ограничив спектр из предыдущего пункта частотой F , обнуляя отсчёты спектра с индексами, большими F , с последующим выполнением обратного преобразования Фурье, вычисляем следующее приближение значений яркостей для заполнения лакуны.

• 6.    Заполняем лакуну значениями яркости, вычисленными в предыдущем пункте. При этом неискажённая часть изображения (изначально достоверно известная) не подвергается никаким изменениям.

• 7.    Далее циклично выполняем пункты 4, 5,6. При этом каждый цикл (итерацию) F увеличивается на единицу, вплоть до наивысшей возможной. Таким образом, лакуна последовательно заполняется, причём неискажённая часть изображения (изначально достоверно известная) не подвергается никаким изменениям.

В результате выполнения предложенного алгоритма ретушируемая лакуна постепенно заполняется изображением, всё более соответствующим спектру окружающего изображения (изначально достоверно известному).

Сравнение результатов работы МИПВС, интерполяции сплайном и нейронной сетью на тестовом изображении

Поскольку результаты реконструкции утраченного фрагмента изображения зависят в значительной мере от свойств изображения, то выбор тестового изображения является важным моментом. Известно, что интерполяция сплайном в первую очередь опирается на пиксели, непосредственно прилегающие к лакуне. Полученное с помощью сплайна изображение страдает отсутствием мелких деталей и имеет «сглаженный» вид.

Заполнение лакун с помощью интерполяции сплайном по определению не может восстановить никакой структуры отсутствующих частей изображения (тем более если их нет вне лакуны), поскольку использует информацию только о краях лакун и плавно заполняет реконструируемое пространство содержанием, подобным своим точкам опоры.

При использовании Movavi, опирающегося на нейросети [20], для реконструкции изображения в лакуне возникнут определённые трудности, если часть изображения, которая должна быть на месте лакуны, не имеет фрагментов, аналогичных остальной части изображения.

МИПВС при заполнении лакуны использует спектральные преобразования. Поэтому при реконструкции анализируется целиком всё изображение, как и в методе, основанном на нейронных сетях. Однако ценой за это будет значительное снижение скорости работы по сравнению с упомянутыми выше методами. Кроме этого, при увеличении размера лакуны будут увеличиваться ошибки заполнения.

Исходя из вышесказанного, выберем заполнение тестового изображения согласно следующим выражениям:

Y [ x , y ] = A [ y ](0,5 – abs(0,5 N – x )) /(0,5 N ) + A o ,

A[y] = Am{(Ra –abs(0,5N – y))/Ra}2, если –Ra < y – 0.5N < Ra, A[y] =0, для остальных y, где N =256 – размер изображения, Ao – «основная» яркость изображения, Am + Ao – максимальная яркость изображения, Ra = 80 – половина размера части изображения, где изменяется яркость, abs(x) – модуль x. На рис. 1 представлены исходное тестовое неискажённое изображение и изображение с лакуной.

Выбор формы лакуны (эллипс) на изображении обусловлен увеличением проблем с заполнением лакуны.

На рис. 1 в графики зависимости дисперсии ошибки реконструкции от ширины лакуны показывают, что для выбранного тестового изображения, которое является «неприятным» для этих методов, неплохо показали себя сплайн и МИПВС. У нейронной сети дисперсия ошибки значительно больше, поскольку отсутствуют необходимые фрагменты для заполнения лакуны на оставшейся части изображения.

Примеры реконструкции изображений в лакуне, показанной на рис. 1 б , представлены на рис. 2 и 3.

Рис. 3 демонстрирует разрезы (через центр по горизонтали) реконструированного разными методами изображения рис. 1б. На рис. 3б хорошо видно, что в самой проблемной области, т.е. в центре лакуны, работа МИПВС (прерывистая линия) гораздо ближе к исходному неискажённому изображению (сплошная линия), чем заполнение лакуны с помощью сплайна (пунктир) или нейронная сеть (полужирный пунктир). Таким образом, в полном соответствии с объективными показателями (с графиками зависимости дис- персии ошибки реконструкции рис. 1в) и с экспертной оценкой (внимательным рассмотрением рис. 2а-в),

а)

Рис. 1. Исходное ошибки реконст

100-

OL

в)    0

можно констатировать, что МИПВС даёт меньшие ошибки по сравнению с конкурирующими методами.

150\ -----------1----------- J i , --------

--sigF

--- sigS

---- sigM,

10     20    30    40

а)

б) еискажённое изображение МИПВС – прерывистая ли нктир) в зависимости от

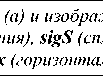
ение с лакуной (б). Графики зависимости дисперсии лайн – пунктир), sigM (нейронная сеть – полужирный льного размера лакуны) (в)

б)

Рис. 2. Примеры реконструкции изображений в лакуне рис. 1б с помощью МИПВС (а), сплайн-интерполяции (б), нейронной сети (в)

в)

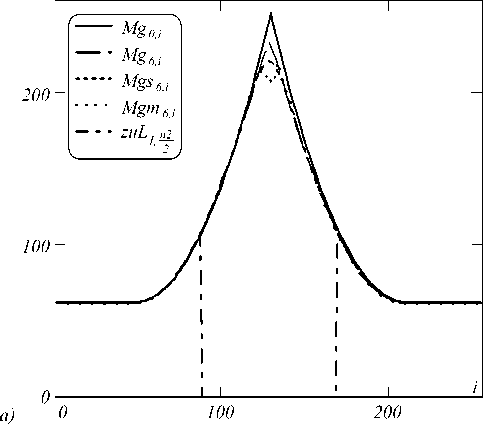
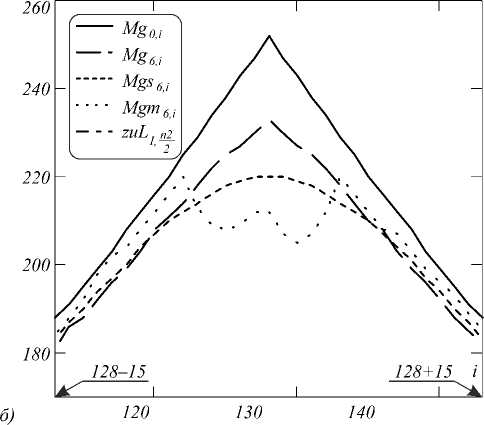
Рис. 3. Разрезы изображений (через центр по горизонтали). По полной ширине изображения (i от нуля до 255 пикселей) (а);

увеличенный масштаб (б). Исходное неискажённое изображение (см. рис. 1а) – сплошная линия (Mg 0 ); исходное изображение с лакуной (см. рис. 1б) – штрихпунктирная линия (zuL); работа МИПВС (см. рис. 2а) – прерывистая линия (Mg); работа сплайна (см. рис. 2б) – пунктир (Mgs); работа нейронной сети (см. рис. 2в) – полужирный пунктир (Mgm)

Сравнение результатов виртуальной реконструкции утерянной части изображения

МИПВС с альтернативными методами

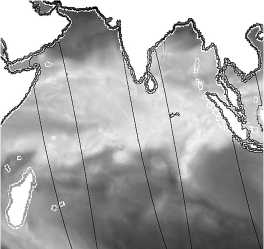
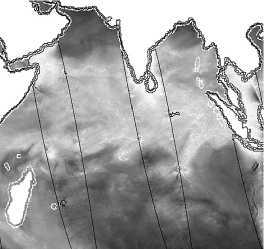
Рис. 4а иллюстрирует поле интегрального паросо-держания атмосферы над Индийским океаном с широкими лакунами, обозначенными чёрным цветом (восстановленного по измерениям спутника AMSR_2 за 01 ноября 2013 года). Перевод иллюстраций в чёрно-белое изображение в данном примере сделан оригинальной процедурой, любезно предоставленной авторами [9], как и оригиналы этих изображений вместе с глобальными цветными картами. Таким образом, градации яркостей непосредственно отображают относительную величину значений поля интегрального паросодержания атмосферы от минимальной (чёрный цвет) до максимальной величины (белый цвет). Для большей наглядности на все восстановленные изображения рис. 4 нами нанесены контуры лакун вместе с географическими контурами. В [9] констатируется, что поскольку лакуны имеют значительную ширину, то дополнение их данными с других спутников, например измерениями с SSMIS F16, F17, отстоящими от измерений AMSR_2 на 3,5–4,5 часа, вызовет существенные погрешности при формировании глобальной карты. Не вдаваясь в подробности методики итерационной схемы построения и пространственновременной интерполяции полей геофизических параметров глобального покрытия по данным спутнико- вых радиометрических наблюдений [9], скажем только, что этот алгоритм предусматривает проводимую в несколько этапов сшивку и интерполяцию данных, полученных с нескольких спутников, пролетавших над интересующей исследователей областью в разное время. Причём эти данные имеют разное пространственное разрешение. В результате используемых в [9] процедур на основании обработки рис. 4а получен рис. 4б. В дальнейшем результаты работы всех остальных методов сравниваются с рис. 4б, который будем считать «идеальным».

Рис. 4 в показывает результаты обработки исходного изображения рис. 4 а методом интерполяции последовательно вычисляемого спектра Фурье. Причём здесь не применяется никаких дополнительных данных с других спутников и никаких априорных знаний (например, данных о градиентах тепловых потоков в известных областях изображения). Результат реконструкции с помощью МИПВС выявляет восстановление основной структуры изображения даже в широких лакунах. Таким образом, с точки зрения реконструкции в реальном времени восстановление содержимого лакун с помощью МИПВС (рис. 4 в ) выглядит вполне приемлемо. Поскольку при заполнении пропусков данных дистанционного зондирования в [9] делается не только пространственная, но и временная интерполяция, то прямое сравнение рис. 4 б и 4 в возможно только в некотором приближении.

а)

б)

г)

е)

Рис. 4. Исходное изображение поля интегрального паросодержания атмосферы над Индийским океаном с лакунами, обозначенными чёрным цветом (а); результаты пространственно-временной интерполяции исходного изображения по многоэтапной процедуре из [9] (б); результаты обработки исходного изображения с помощью МИПВС (в); результаты обработки исходного изображения интерполяцией сплайном (г). Результат заполнения лакуны изображения (а) с помощью: нейронной сети (д), с помощью image inpainting (е)

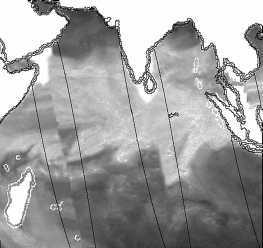
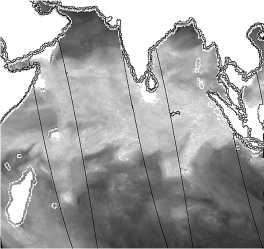
Различия результатов [9] с МИПВС, помимо погрешностей реконструкции, могут быть объяснены тем обстоятельством, что между пролётами первого и следующего спутника проходит определённое время и общая картина меняется.

На рис. 4 г лакуны заполняются с помощью сплайн-интерполяции [13, 14]. Рис. 4 д демонстрирует применение технологии нейронной сети. Рис. 4 е показывает результаты работы image inpainting [15].

Сплайн, опираясь на данные, расположенные по кра- ям лакун, лишь плавно ретуширует утерянные данные. Нейронные сети демонстрируют в данном случае все свои характерные недостатки: проблемы с не- прерывностью структуры и согласованностью текстур с явно видимой сшивкой посередине лакун. Та- кие же проявления характерных недостатков, как у нейронной сети, видны на рис. 4е, полученном image inpainting [15]. В то время как МИПВС не просто ре- туширует лакуны, а частично восстанавливает их со- держимое.

Для объективного сравнения работы методов по заполнению (восстановлению) лакун необходимо иметь эталонные неискажённые объекты, на которые вносятся контролируемые изменения (изъятия заданных областей изображений). В этом качестве используем десять фрагментов, вырезанных в разных местах из полностью заполненной (интерполированной по многоэтапной процедуре) карты поля интегрального паросодержания атмосферы, предоставленной нам авторами [9] рис. 5.

° XY

N 1 N 2

N 1 -1 N 2 -1          _         _

ZZ ( X j - X X Y , -- Y ), i =0 j =0

где N 1 , N 2 – ширина и высота изображения.

Кроме того, полезным может быть вычисление меры резкости цифрового изображения (МРЦИ) в реконструированной лакуне [19] и её сравнение с эталонным образцом (оценка того, какой из методов по этому критерию оказался ближе к оригиналу).

МРЦИ вычисляется согласно алгоритму [19]:

• 1)    ввести на вход анализируемое полутоновое изображение I ;

• 2)    задать размеры двух масок для усредняющего фильтра k 1 и k 2;

• 3)    получить изображение B 1, выполнив свертку исходного изображения I с усредняющим фильтром размером k 1;

• 4)    получить изображение B 2, выполнив свертку исходного изображения I с усредняющим фильтром размером k 2 ( k 2 >k 1);

• 5)    получить оценку степени размытости С :

  

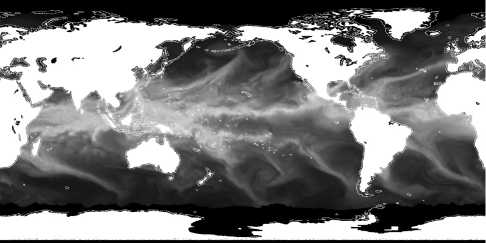
  Рис. 5. Исходное изображение поля интегрального паросодержания атмосферы, интерполированное по многоэтапной процедуре [9]

  
  

  Удалим на выбранных фрагментах часть изображений, то есть создадим лакуны. Форма лакун соответствует случаям аэрокосмических изображений. При этом варьируем ширину нижней части моделируемой лакуны от 8 до 96 пикселей. Примеры двух фрагментов с шириной лакуны в нижней части изображений, равной 64 пикселям, приведены на рис. 6. Произведём заполнение лакун разными методами. И в заключение вычислим объективные показатели качества восстановленных разными методами изображений в смоделированных лакунах – среднеквадратичное отклонение (СКО) и меру структурного подобия (МСП). МСП (или в английском варианте SSIM) рассчитывается по формуле [16]:

  
  

  N 1 -1 N 2 -1 c = zz—

  I ij - B 2 ij

  N 1 N 2

  где N 1 , N 2 – ширина и высота изображения.

  а)

  

  г)

  Рис. 6. Примеры исходных изображений поля

  
  

  SSIM =

  
  

  ^^^^^  ^^^^^

  о xy || 2 XY || 2 ° x о y о X ° _Y JI X ² + Y ² JI ° X ² + ° _Y ²

  
  

  где X , Y – средние значения яркостей пикселей изображений X и Y , где

  
  
  
  
  
  

  о

  
  
  
  

  N 1 N 2

  
  

  N 1 -1 N 2 -1

  ZZ ( x j - X )²,

  
  

  N 1 N 2

  
  

  N i -1 N 2 -1

  ZZ (Y j - Y )²,

  
  

  в)

  интегрального паросодержания атмосферы (а, в) (слева) и те же изображения, но с модельными лакунами (б, г) (справа)

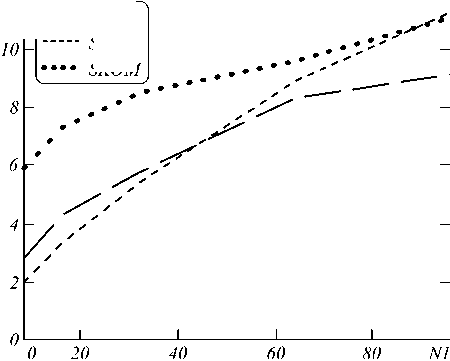
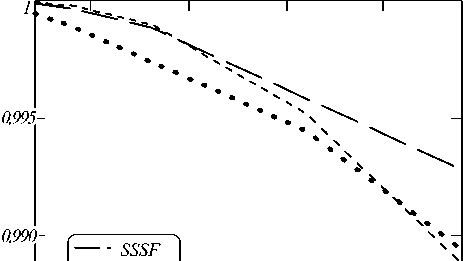
  Сопоставление и анализ графиков на рис. 7, 8 позволяет высказать утверждение, что предлагаемый нами МИПВС с точки зрения объективных критериев (СКО и МСП) вполне конкурентоспособен по сравнению с альтернативными методами. В основном СКО МИПВС от эталона рис. 7 (особенно в широких лакунах) оказывается меньше, чем для сплайна и нейронной сети. В то же самое время мера структурного подобия для МИПВС (сплошная линия рис. 8) имеет лучшие показатели, чем для других методов. При этом МСП достигает максимума (единицы) на полностью совпадающих изображениях.

  
  

  Рис. 9 иллюстрирует зависимость меры резкости цифрового изображения (МРЦИ) от ширины нижней 12

  
  
  

  --SKOF

SKOS

SKOM части моделируемой лакуны для соответствующих фрагментов изображений рис. 6а, б.

а)

б)

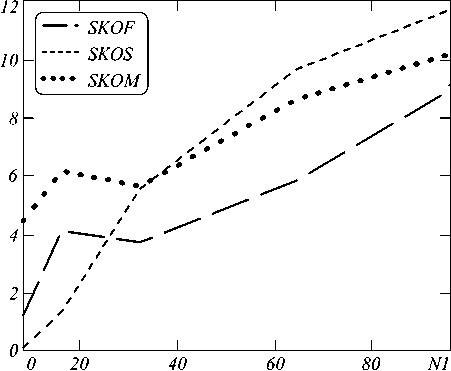
Рис. 7. СКО, вычисленные для фрагментов рис. 6а, б соответственно: SKOF (МИПВС – прерывистая линия), SKOS (сплайн – пунктир), SKOM (нейронная сеть – полужирный) в зависимости от N1 (ширина нижней части моделируемой лакуны)

0,995-

0,990-

--SSSF

ssss

SSSS

•••• SSSM

SSSM

0,985-------------1111-------------------

• а)    ’ 0    20         40         60         80 Ml

0,985------L

• б)    ’ 0    20

N1

Рис. 8. МСП, вычисленные для фрагментов рис. 6а, б соответственно: SSSF (МИПВС – прерывистая линия), SSSS (сплайн – пунктир), SSSM (нейронная сеть – полужирный пунктир) в зависимости от N1 (ширина нижней части моделируемой лакуны)

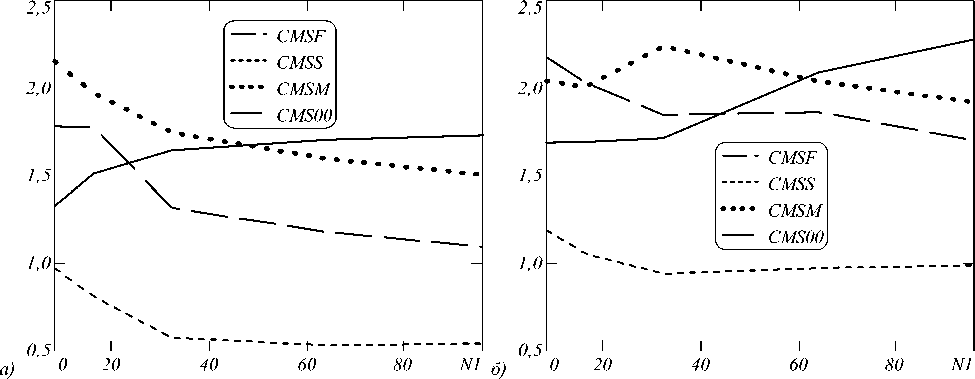
Рис. 9. МРЦИ, вычисленные для фрагментов рис. 6а, б соответственно: CMSF (МИПВС – прерывистая линия), CMSS (сплайн – пунктир), CMSM (нейронная сеть – полужирный пунктир), CMS00 (исходные неискажённые данные – сплошная линия) в зависимости от N1 (ширина нижней части моделируемой лакуны)

Из рис. 9 следует, что сплайн (пунктир) с точки зрения МРЦИ значительно проигрывает как нейронным сетям, так и МИПВС, так как он заполняет лакуну плавно меняющейся яркостью, в то время как МИПВС и нейронная сеть имеют значения, близкие к собственным значениям исходного эталонного изображения.

Необходимо заметить, что показатели, вычисленные по объективным критериям, сильно зависят от вида изображения. То есть если лакуна находится на низкоконтрастном изображении, то приведённые выше критерии могут выдать противоречивые результаты. Это вполне объяснимо тем обстоятельством, что в предельном случае равномерный фон хорошо интерполируется простым сплайном, в то время как другие методы вполне могут дать большее отклонение от оригинала.

Таким образом, проведя сравнительный анализ по объективным критериям и приняв во внимание, в том числе и экспертную оценку, можно утверждать, что МИПВС является конкурентоспособным. Следовательно, его, наряду с другими методами, можно применять в задачах заполнения лакун в аэрокосмических изображениях.

Заключение

В данной работе проводился сравнительный анализ методов, применяемых при заполнении лакун на изображениях. Это интерполяция кубическим сплайном, нейронная сеть и метод интерполяции последовательно вычисляемого спектра Фурье. Сравнение сделано как на модельных примерах, так и на реальных изображениях. Интерполяция кубическим сплайном, как и методы image inpainting, реализованные с помощью нейронных сетей, не позволяют восстанавливать изображения в сплошных лакунах.

В ряде случаев содержимое пикселей изображения может быть взаимозависимо, несмотря на то, что эти пиксели находятся на значительном расстоянии. Это может быть связано с условиями регистрации изображения [3, 4]. Другой причиной взаимозависимости яркости пикселей могут быть физические процессы, влияющие на изображение. Случай с глобальной картой поля интегрального паросодержания атмосферы ярко иллюстрирует этот вариант. Эта взаимозависимость яркостей пикселей даёт возможность МИПВС реконструировать изображение в лакуне.

Был проведён сравнительный анализ по объективным критериям (СКО, мера структурного подобия, мера резкости цифрового изображения). Из него следует, что МИПВС является конкурентоспособным, и его, наряду с другими методами, можно применять в задачах заполнения лакун в аэрокосмических изображениях.