Реверсивный стеганографический метод сокрытия информации, основанный на интерполяции изображений

В последнее десятилетие методы сокрытия данных превратились в важное направление исследований в области информационных технологий. Широкое распространение Интернета и развитие цифровой коммуникации породили проблему обеспечения безопасности передачи информации по открытым каналам связи. Для решения проблемы были разработаны новые методы безопасности секретной коммуникации. Параллельно с развитием цифровой техники получила развитие и цифровая стеганография – наука о сокрытии информации [8, 9, 11, 12].

Обычно секретная информация внедряется в такие цифровые носители, как цифровые файлы, изображения, видео, тексты, аудио, которые передаются по открытым каналам связи без предварительной шифровки. Стеганография успешно применяется в различных направлениях, таких как медицина, военное дело, надзор над сохранением авторских прав на используемые материалы и циркуляция секретных данных и т.д. По типу решения задачи различают алгоритмы встраивания и извлечения секретных данных.

Наиболее популярным является стеганография изображения, в котором информация внедряется в изображение-контейнер. Термин «контейнер» означает цифровое медиа, используемое для внедрения секретного сообщения. Внедряемая информация называется «секретное сообщение». Изображение, в которое уже внедрено секретное сообщение, называется «изображение со встроенной информацией». Для внедрения секретного сообщения в контейнер разработано множество процедур и алгоритмов, отличающихся своими показателями. Изображение со встроенной информацией, передаваясь по открытым каналам связи, доходит до получателя и подлежит извлечению из него секретного сообщения. Для этой цели разрабатываются и используются соответствующие методы и алгоритмы [12– 16]. Все методы и алгоритмы характеризуются следующими характеристиками:

• •    Объём внедрения - это максимально возможная величина внедрения.

• •    Визуальное качество изображения - это то, насколько изображение со встроенной информацией идентично пустому изображению.

• •    Безопасность алгоритма - это способность изображения со встроенной информацией противостоять всевозможным атакам, направленным на обнаружение секретного сообщения.

Все разработанные алгоритмы отличаются друг от друга по области внедрения даты в изображение, типу контейнера и методу внедрения. Таким образом, идеальный стеганографический метод должен обладать максимальным объёмом внедрения, высоким визуальном качеством. Недостатком стеганографических методов является относительно низкий объём внедряемой даты и вызванные этим внедрением искажения исходного изображения. В свете сказанного в этой области есть ещё много проблем, требующих своего решения. Вышеупомянутое вдохновляет сообщество исследователей на разработку новых стеганографических технологий для передачи секретных сообщений и более безопасного обмена секретными данными.

Схожие работы

В стеганографии изображения для повышения качества контейнера, т.е. увеличения его разрешения, используется метод интерполяции. В 2009 году Jung и Yoo [2] предложили использование этого метода в стеганографии изображений. Суть этого метода заключается в уменьшении исходного изображения размером M ×N до двух изображений размером

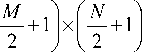
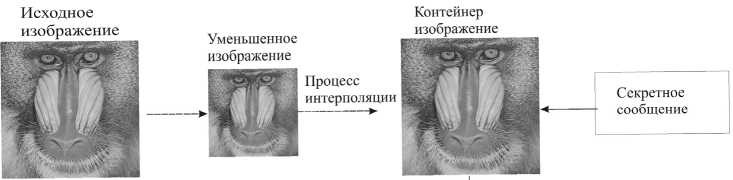
Метод Jung состоит из двух основных шагов: интерполяции изображения и сокрытия секретных данных. На первом этапе исходное изображение делится на блоки 3 × 3, а затем расширяется до первоначального размера с использованием алгоритма интерполяции. На втором этапе секретная дата вставляется в сгенерированный на первом этапе контейнер с использованием алгоритма сокрытия секретных данных. Процесс сокрытия информации реализуется по схеме (рис. 1).

Используя метод NMI (Ne i gnbour Mean Interpolation), сокращённые изображения преобразуются в контейнер размером M ×N. Затем это изображение делится на несколько блоков. Контейнер и пиксели каждого из его блоков, за исключением первого, могут быть использованы для внедрения информации. Объём внедрения в каждый пиксель зависит от разницы между этим и первым. Для увеличения объёма внедрения метод интерполяции комбинируется с методом LSB.

Секретное сообщение

Изображение со встроенной информацией

Рис. 1. Схема сокрытия информации

Впоследствии были разработаны несколько разновидностей метода интерполяции изображения, которые в настоящее время применяются в стеганографии. В литературе описаны наиболее успешные методы: NMI (Neighbor Mean Interpolation) [2], INP (Interpolation by Neighboring Pixel [3] и NIE (New Interpolation Expansion) [1]. Все эти методы направлены на разработку новых методов интерполяции и являются модификациями метода Jung. Несмотря на некоторые преимущества, после внедрения секретной даты качество изображения со встроенной информацией становится хуже, чем качество интерполированного изображения. В работе [3] контейнер разделён на блоки 2 × 2, четыре соседних пикселя используются для определения максимального значения четырёх соседних пикселей каждого блока, которые, в свою очередь, используются для вычисления наибольшей разницы между готовыми к внедрению пикселями. Однако несмотря на увеличение объёма внедрения, ка- чество изображения снижается. Sabeen Govind и др. [5] разработали двухэтапную схему сокрытия данных, обеспечивающую большой объём внедрения. На первой стадии интерполяции исходное цифровое изображение превращается в изображение-контейнер с использованием техники ENMI (Enhansed Neighbour Mean Interpolation) алгоритма. Разницы между значениями исходного изображения и контейнера складываются, а полученная сумма делится на число слагаемых. Полученный результат записывается в среднюю ячейку блока контейнера. Однако несмотря на более высокое значение объёма внедрения, визуальное качество изображения со встроенной информацией не слишком высокое, а сам алгоритм сложен для вычислений. Ahmad. A. Mohammad и др., преследуя цель повышения объёма внедрения и качества изображения, достигнутые в работе Jung, разработали новый метод сокрытия данных, основанный на интерполяции изображения, для обеспечения высокого объёма внедрения. Декларируется, что предлагаемый метод отличается относительной простотой расчетов. Другим достижением является весьма малое искажение изображения. Эти искажения при использовании методов интерполяции возникают на этапах уменьшения и увеличения размеров изображения и сокрытия данных. Для уменьшения искажений изображения при вышеприведённых процедурах разработан алгоритм интерполяции изображений. Но следовало бы отметить, что их метод фактически был модификаций метода Jungа.

Jana В.I. и др. [4] предложили новый реверсивный метод сокрытия данных, основанный на методе Weight matrix и отличающийся большим объёмом внедряемой даты. Согласно этому методу исходное изображение размером M (высота), N (ширина) увеличивается дважды путём интерполяций. В результате с использованием разработанных авторами специальных преобразований получается изображение с высотой (2XM-1) и шириной (2XN-1). Затем исходное изображение делится на блоки (3 × 3), а изображение-контейнер – на блоки (5 × 5). Секретная информация внедряется в вычисленную позицию блока изображения-контейнера с (5 × 5). Этим путём достигается большой объём внедрения и реверсивность алгоритма. Однако несмотря на теоретические преимущества, сложность алгоритма усложняет его вычислительные способности, что, в свою очередь, ограничивает практическое использование метода.

Предлагаемый метод сокрытия даты

В этом параграфе предлагается новый реверсивный метод сокрытия секретной информации, основанный на интерполяции изображения.

Преимуществом метода является обеспечение большого объёма внедряемых секретных бит при более высоких значениях визуального качества изображения со встроенной информацией.

Предлагаемый метод сокрытия информации реализуется по схеме сокрытия информации (рис. 1.), который, в свою очередь, состоит из следующих этапов:

• •    уменьшение изображения;

• •    расширение изображения;

• •    сокрытие информации;

• •    извлечение информации.

Реверсивность достигается по отношению к «уменьшенному изображению», но не к исходному полноразмерному.

Поэтапное выполнение операций по цифровой реализации метода и обработке изображений, в которые внедряются секретные биты, приводится ниже.

Последовательность шагов на этапе внедрения.

Шаг 1. Оригинальное изображение, разделяясь на блоки 3 × 3, подвергается интерполяции. Для этой цели используется формула (1).

C (0,0) - 0 (0,0),

C (0,1) - ( C ( 0,0 ) + C ( 0,2 ) ) /3 + ( C ( 2,0 ) + C ( 2,2 ) ) /6,

C ( 1,0 ) - ( C ( 0,0 ) + C ( 2,0 ) ) /3 + ( C ( 0,2 ) + C ( 2,2 ) ) /6,(1)

C ( 1,1 ) - ( C ( 0,0 ) + C ( 0,2 ) + C ( 2,0 ) + C ( 2,2 ) ) /4.

Шаг 2. Путём интерполяции генерируется контейнер. Полученное изображение делится на блоки 2 × 2. В предлагаемом алгоритме сокрытия информации пиксели, находящиеся в верхней правой части блока, в нижней части слева и в нижней части справа, пригодны для внедрения секретного сообщения. Используя координаты (2), обозначим пиксели блоков как d 1 , d 2 , d 3 :

d 1 - ma (| C ( 0,1 ) - C ( 0,0 )|,| C 1 ( 0,1 ) - C 2 ( 0,0 )|) , d 2 - ma ( C ( 1,0 ) - C ( 0,0)|, C ( 1,0 ) - C 3 ( 0,0 d 3 - ma ( C 1 ( 1,1 ) - C 1 ( 0,0)|, C ( 1,1 ) - C 2 ( 0,0)| I C 1 ( 1,1 ) - C 3 ( 0,0)| ,| C 1 ( 1,1 ) - C 4 ( 0,0)|).

Шаг 3. После нахождения трёх значений разниц для определения количества секретных бит, подлежащих внедрению в каждый пиксель, десятичные значения результатов, полученных от вычислений по формуле (2), переводятся в двоичную систему. В цифровом ряде, полученном от этого системного преобразования, количество бит равняется количеству бит, подлежащих внедрению.

Шаг 4. Если принять секретную дату как b 1 , b 2 , b 3 , то они могут быть внедрены с помощью (3):

5 1 ( 0,1 ) -

5 2 ( 1,0 ) -

5 3 ( 1,1 ) -

C 1 ( 0,1 ) + b 1 ,ifC 1 ( 0,1 ) <  0 1 ( 0,1 ) , C 1 ( 0,1 ) - b [, иначе ;

C 1 ( 1,0 ) + b 2 , if C 1 ( 1,0 ) < 0 1 ( 1,0 ) , C 1 ( 1,0 ) - b ₂ иначе ;

C 1 ( 1,1 ) + b 3 ,ifC 1 ( 1,1 ) <  0 1 ( 1,1 ) , C 1 ( 1,1 ) - b 3 иначе .

Здесь С ( i , j ) представляет собой пиксели контейнера, а с S ( i , j ) являются пикселями изображения со встроенной информацией, в которые внедрена секретная дата.

Полученные пиксели выглядят как на рис. 2.

C(0,0)	C(0,1)
C(1,0)	C(1,1)

S(0,0)	S(0,1)
S(1,0)	S(1,1)

Рис. 2. Блоки: контейнера (а) и изображения со встроенной информацией (б)

Сравнивая пиксели контейнера и изображения со встроенной информацией, заметим, что изменения в пикселях незначительны. При замене процедуры логарифмирования преобразованием десятичной системы в двоичную, количество бит секретной даты становится больше, что, в свою очередь, означает увеличение объёма внедрения. Кроме того, из-за уменьшения изменений в пикселях значение PSNR получается высоким.

Цифровой пример встраивания

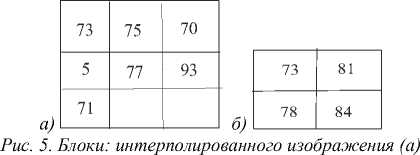
Исходное изображение путём интерполяции по формуле (1) преобразуется в контейнер. По формуле (2) вычисляются разницы d 1 , d 2 , d 3 .

Найденные десятичные значения разниц между пикселями переводятся в двоичную систему исчисления

n1 - 7 -111,

n2 - 6 -110,                                     (4)

nз -16 -10000.

После перевода значений d в двоичную систему выбираются биты секретной даты, количество которых равняется количеству нулей (0) и единиц (1) двоичных чисел. Например, если заданы биты секретной даты b 1 = 11001100111100011, то при n 1 =7= 111 первые 3 бита секретной даты b 1 = 110. После перевода этого значения в десятичную систему исчисления b 1 =6. На очередном этапе сравниваются пиксели контейнера и изображения со встроенной информацией.

Если пиксели контейнера меньше, чем пиксели исходного изображения, то выбранные секретные биты добавляются к пикселю контейнера. В противном случае выбранные секретные биты вычитаются из пикселя контейнера. Таким образом, уменьшается разница между контейнером и изображением со встроенной информацией. А это означает повышение PSNR.

S1 - 75 + 6 - 81,

S2 - 75 + 3 - 78,                                (5)

Sз -77 + 7-84.

Таким образом, формируются пиксели изображения со встроенной информацией.

73	81
78	84

Рис. 3. Пиксели блока изображения со встроенной информацией

Если сравнить пиксели контейнера и изображения со встроенной информацией, заметим, что разница между пикселями очень небольшая. В результате замены процедуры логарифмирования на процедуру перевода разницы значений пикселей контейнера n из десятичной системы в двоичную количество бит секретной даты, подлежащих внедрению в ковер-изображение, возрастает. Это, в свою очередь, озна- чает увеличение объёма внедрения секретной даты и является преимуществом предлагаемой схемы по сравнению с другими методами, что и является основной задачей настоящего исследования.

Шаги фазы извлечения

Алгоритм извлечения секретного сообщения из изображения со встроенной информацией, будучи противоположностью алгоритма внедрения, используется для выделения скрытой даты и восстановления исходного изображения.

Шаг 1. Изображение со встроенной информацией делится на блоки 2 × 2, а интерполированное изображение-контейнер вновь восстанавливается. Полученные результаты используются для извлечения секретного сообщения.

C(1,1)	C(l,2)	C(1,3)
C(2,1)	C(2,2)	C(2,3)
C(3,1)	C(3,2)	C(3,3)

S(1,1)	S(1,2)
S(2,1)	S(2,2)

Рис. 4. Блоки: контейнера (а) и изображения со встроенной информацией (б)

Затем из пикселей изображения со встроенной информацией вычитаются пиксели изображения-контейнера.

De1 - C(1,2)-S(1,2),

De 2 - C (2,1)-S (2,1),

De 3 - C (2,2)-S (2,2).

Из полученных значений разниц изображения со встроенной информацией и контейнера восстанавливаются биты секретной даты .

Цифровой пример фазы извлечения

Изображение со встроенной информацией делится на блоки 2× 2, а интерполированное изображение-контейнер вновь восстанавливается и используется в процессе извлечения.

и изображения со встроенной информацией (б) Из пикселей изображения со встроенной информацией вычисляются пиксели контейнера

81–75=6=110,

78–75=3=11,

84–77=7=111.

Из полученных значений вычисленных разниц формируются биты секретных данных, которые передаются по открытому каналу связи.

Результаты экспериментальных исследований

С целью проверки достоверности полученных результатов исследования были проведены эксперименты на стандартных серых снимках размером 512×512, взятых из базы данных изображений USC-SIPI, 8 из которых показаны на рис. 2. Эксперименты были проведены с использованием MATLAB \ R2014b.

Для оценки качества изображения со встроенной информацией использовалась метрика RSNR, значение которой вычислялось методом Peak Signal to Noise Ratio (RSNR) по формуле:

PSNR = lOlog io

__________255x 255__________

P * Q I n "i [ CI ⁽ mⁿ ) " SI ( m , ⁿ ) J 2

, (7)

которая определяет степень схожести двух сравниваемых снимков. Зрительная система человека не способна улавливать разницу свыше 36 dB. Значение PSNR прямо связано с визуальным качеством изображения со встроенной информацией. Чем больше его значение, тем больше сходство сравниваемых изображений. P и Q обозначают размер изображения, а CI и SI – вид изображения. Заранее отметим высокие средние значения показателей тестированных изображений, которые равняются по сокрытию данных – 435202; PSNR – 38,8096.

Затем рассчитывались величины PNSR между контейнером и изображением со встроенной информацией, которые приводятся в табл. 1. В таблице приведены данные сравнения PSNR предлагаемого метода с новыми методами, разработанными в последние годы.

Табл. 1. Сравнение показателей алгоритмов

Исходное изображение	Метрики	Yong-qing Chen и др.[ 17]	Malik А.и др. [18]	Предлагаемый метод
Lena	PSNR Capacity	34,18 369,715	31,93 144,887	38,56 564,744
Baboon	PSNR Capacity	24,69 651,710	22,85 187,141	36,47 546,791
Airplane	PSNR Capacity	32,84 334,328	30,26 151,269	35,88 524,719
Peppers	PSNR Capacity	32,82 374,589	30,42 144,177	39,32 656,611
Sailboat	PSNR Capacity	31,80 364,589	29,04 175,183	33,36 378,123
Boat	PSNR Capacity	29,82 343,589	32,22 124,236	35,93 369,563
Couple	PSNR Capacity	26,82 381,589	24,36 354,137	29,68 400,021
House	PSNR Capacity	32,02 236,589	31,32 235,325	36,21 282,753
Средние значения	PSNR Ёмкость встраивания	30,26 382,087	29,05 189,544	35,60 465,415

г)

Рис. 6. Контрольные изображения

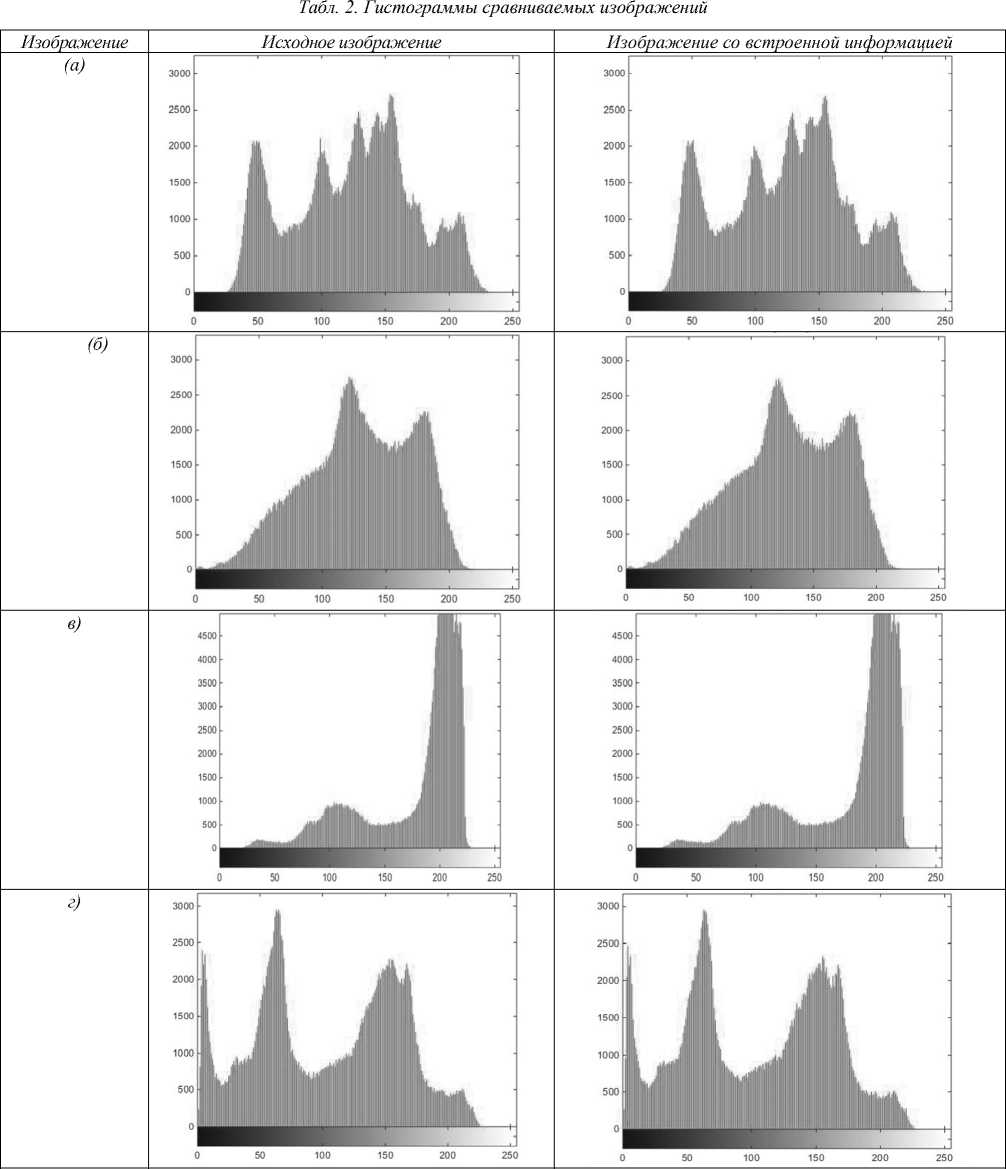
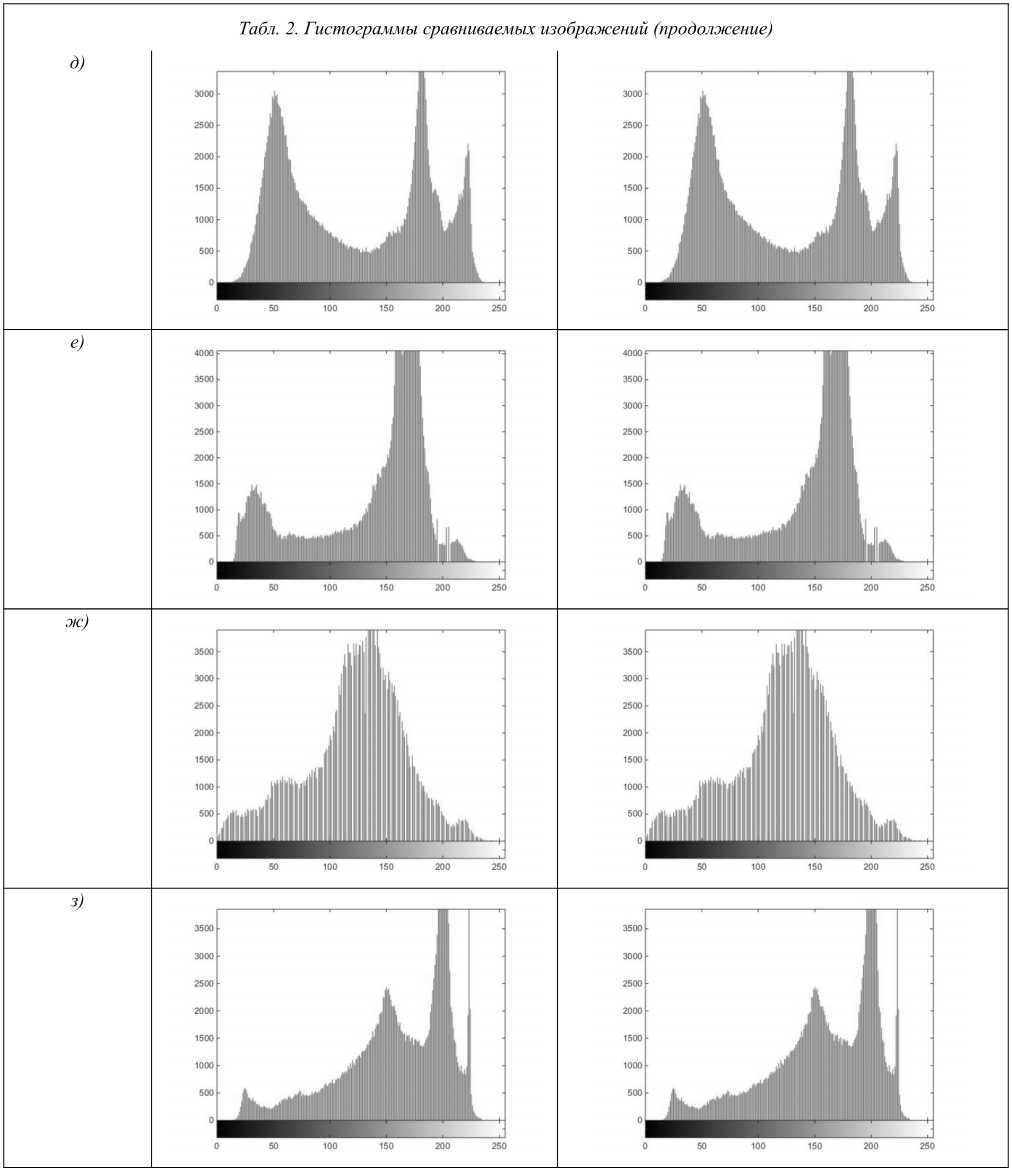
Более высокие значения PSNR и объёма внедрения указывают на превосходство предлагаемого метода над другими сравниваемыми. Все изображения имеют PSNR свыше 36 dB, что говорит о том, что неизбежные и связанные с внедрением секретных данных искажения остаются незаметными для человеческого глаза. Кроме PSNR, для получения более точных результатов сравнения исходного и изображений со встроенной информацией нами был использован также графический метод гистограмм.

В табл. 2 приведены гистограммы исходных и соответствующих им изображений со встроенной информацией. Из таблицы видно, что все сравниваемые изображения имеют почти одинаковые гистограммы. Это свидетельствует о высокой степени идентичности сравниваемых изображений, из-за чего обнаружение наличия секретной информации становится невозможным.

Заключение

Предложен реверсивный метод сокрытия секретных данных, отличающийся большим объёмом внедрения секретной информации. Разработанный алгоритм основан на концепции интерполяции изображений. Известно, что высокое качество изображения и объём скрываемой информации прямо противоположны друг другу. Целью настоящей работы была разработка алгоритма, отличающегося большим объёмом внедряемой информации при сохранении высокого качества изображения со встроенной информацией. Это было достигнуто путём использования нового механизма внедрения, путём замены процедуры логарифмирования процедурой перевода данных из десятеричной системы исчисления в двоичную. Эффективность предлагаемого метода была доказана экспериментальными исследованиями, проведённы- ми на множестве контрольных изображений. Сходство сравниваемых, исходных и изображений со встроенной информацией подтверждалось методами RSNR и гистограмм.

Высокие значения визуального качества изображений не менялись в зависимости от объёма внедрения и вида контрольных изображений. Из сказанного выше можно заключить, что предлагаемый нами реверсивный метод сокрытия информации обеспечивает лучшее визуальное качество изображения со встроенной информацией и более высокий объём сокрытой даты по сравнению с другими приведёнными в литературе.

Referencs

• [10]    Sabeen GPV, Judy MV. A secure framework for remote diagnosis in health care: A high capacity reversible data hiding technique for medical images. Comput Electr Eng 2020; 89(25): 300-314.

• [11]    Niels P, Peter H. Hide and Seek: an introduction to ste-ganography. IEEE Secur Priv 2003; 99(5): 32-44.

• [12]    Kriti DN, Dabahdeh DS. A survey on image steganography & its techniques in spatial & frequency domain. Int J Recent Innov Trends Comput Commun 2014; 3(2): 776-779.

• [13]    Bin Li, Janhui H, Jiwu H, Yun QS. A Survey on Image Steganography and steqanalysis. J Inf Hiding Multimedia Signal Process 2011; 2(2): 142-172.

• [14]    Nazinder K, Amanjot K. Art of steganography. Int J Adv Trends Comput Appl 2017; 4(2): 30-33.

• [15]    Neil FJ, Stefan CK. A survey of steganography techniques. In Book: Katzenbeisser S, Petitcolas FA, eds. Information hiding techniques for steganography and digital watermarking. Ch 3. Norwood: Artech House Inc; 1999: 43-78.

• [16]    Naghiyeva A, Akbarzadeh K, Verdiyev S. New steganog-raphy method of reversible data hiding with priority to visual quality of image. 2nd Int Conf on Advances in Computing, Communication, Embedded and Secure Systems (ACCESS) 2021: 329-333.

• [17]    Chen Y, Sun W, Li L, Chang C, Wang X. An efficient general data hiding scheme based on image interpolation. J Inf Secur Appl 2020; 54(6): 271-350.

• [18]    Malik A, Sikka G, Verma HK. Image Interpolation based hight capacity reversible data hiding scheme. Multimed Tools Appl 2017; 76(22): 24107-24123.

Сведения об авторах

Нагиева Абабил Фахраддин гызы , 1993 года рождения, в 2014-м году окончила Азербайджанский государственный аграрный университет по специальности «Инженерия информационных технологий и систем. Является докторантом кафедры компьютерной инженерии и телекоммуникации Азербайджанского технологического университета. Область научных интересов: защита информации, стеганография.

ГРНТИ: 81.93.29