Review of Segmentation Methods for Brain Tissue with Magnetic Resonance Images

Published Online March 2014 in MECS DOI: 10.5815/ijcnis.2014.04.07

Image segmentation plays a vital role in Image Analysis and computer vision, which is considered as the obstruction in the development of image processing technology [1]. Typically, Image Segmentation is a process of partitioning an image into non - overlapping, constitute regions which are homogeneous with respect to some characteristics such as intensity, color and texture [2]. Image Segmentation has a wide application in areas such as robot vision, geographical Imaging, object recognition and mainly used in the area of medical Imaging. Medical Imaging include surgical planning [3], Multimodality Image Registration [4], Abnormality Detection [5], Brain Tumor Detection [6] etc. Medical Image Segmentation partitions a volumetric medical Image into separate regions to indicate its tissue type or anatomical structure that are meaningful for a specific task and also play a critical role in the treatment outcome. Medical Imaging Technology provides the clinician with a number of complementary diagnostic tools such as Computer Tomography (CT), Ultrasound, X-ray, Magnetic Resonance Imaging (MRI) and Positron Emission Tomography (PET). Routinely these images are interpreted visually and qualitatively by radiologists. Advanced research requires quantitative information, such as size of brain ventricles after a traumatic brain injury or the relative volume of ventricles to brain [7]. It is observed that from different modality magnetic resonance imaging( MRI) is the most widely used modality which provides rich information about human anatomical structure due to its high spatial resolution, high signal to noise ratio and excellent discrimination of soft tissue. Besides all these good properties, Magnetic Resonance Imaging suffers from three considerable obstacles: noises, partial volume effect (PVE) and intensity non - uniformity (INU); out of which intensity non-uniformity is the most important obstacles. Partial volume effect (PVE): means artifacts that occur where multiple tissues types contribute to a single pixel, resulting in blurring of intensity across boundaries, which is common in medical images. Intensity non-uniformity (INU): is a spatially slow varying function that makes the pixels belonging to same tissue to be observed with different intensity. In order to produce a correct segmentation of MR Images the intensity non - uniformity (INU) artifact needs to be modeled and compensated. In homogeneities in magnetic resonance (MR) images are usually categorized by their origin. Device related to INU artifacts can be efficiently compensated via calibration methods based on prior information obtained by using a uniform phantom[8]. Alternatively, INU artifacts related to the shape, position, structure and orientation of the patient [9] are much more difficult to handle[10]. Several retrospective INU compensation approaches have been reported, which include homomorphic filtering[11,12], polynomial or B-spline surface fitting based on intensity[13]or gradient [14], segmentation based techniques via maximization likelihood estimation[15], Markov random fields[16], fuzzy c-means clustering[17,18,19], or nonparametric estimation[20]. Further INU compensation procedures based on histogram involve high-frequency maximization [21], information maximization [22], or histogram matching [23].The most complete review of INU compensation techniques can be found in [10].

For detection of brain abnormality using Magnetic Resonance Imaging modality the entire brain image is subdivided into sub - regions, other than background such as white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF) [9]. Due to varying complications in segmenting human cerebral cortex, the manual methods for brain tissue segmentation lead to errors both in terms of accuracy and reproducibility and also time consuming. As most brain structures are anatomically defined by boundaries of these tissues classes, thus a method to segment tissues into these categories is an important step in quantitative morphology of the brain [10]. Hence, fast and accurate segmentation technique is required [11].

The rest of the paper is organized as follows: Section II presents the details of fundamental theory of Magnetic Resonance Imaging. Section III presents Image segmentation and its principal methodologies using adaptive spatial fuzzy C - means, Markov Random Field, fuzzy connectedness method and atlas based re - fuzzy connectedness. Section IV gives a comparative analysis of these segmentation approaches in terms of Dice Similarity Coefficient, overlap ratio and Jaccard coefficient. The summary and conclusion are presented in section V.

• II.    MAGNETIC RESONANCE IMAGING

In this section, we give a brief description of the principles of Magnetic Resonance Imaging (MRI). Magnetic Resonance Imaging is primarily a medical Imaging technique mostly used in radiology to visualize the structure and function of the body. It provides detailed images of the body in any plane. MRI provides much greater contrast between different soft tissues of the body than other Imaging modalities [12]. A magnetic field and pulses of radio wave energy is used to make pictures of organs and structures inside the body. By using this Imaging technique anatomy problems can be easily detectable that cannot be seen with other Imaging methods.

In MRI, the image is a map of the local transverse magnetization of the hydrogen nuclei. This transverse magnetization in turn depends on several intrinsic properties of the tissue. The Magnetic Resonance phenomenon relies on the fundamental property that protons and neutrons that make up a nucleus possess an intrinsic angular momentum called spin. When protons and neutrons combine to form nucleus, they combine with oppositely oriented spins. Thus, nuclei with an even number of protons and neutrons have no net spin, whereas nuclei with an odd number of protons or neutrons possess a net spin. Hydrogen nuclei are made up of only a single proton and thus possess a net spin. The human body is primarily fat and water, which have many hydrogen atoms. Medical MRI primarily images the magnetic Resonance signal from the hydrogen nuclei in the body tissues. The net spin of the nucleus around its axis gives it an angular moment. Since the proton is a positive charge, a current loop perpendicular to the rotation axis is also created, and as a result the proton generates a magnetic field. The joint effect of the angular moment and the self-generated magnetic field gives the proton a magnetic dipole moment parallel to the rotation axis. Under normal condition, one will not experience any net magnetic field from the volume since the magnetic dipole moments are oriented randomly and on average equalize one another. When placed in a magnetic field, a proton with its magnetic dipole moment processes around the field axis. The frequency of this precession, m is the resonant frequency and is directly proportional to the strength of the magnetic field, i.e.

m = γͿ                                        (1)

Where J is the main magnetic field strength and γ is a constant called gyro magnetic ratio which is different for each nucleus.

• III.    IMAGE SEGMENTATION AND METHDOLOGY

Image Segmentation is one of the most widespread means to classify correctly the pixels of an image in decision oriented applications. Image segmentation is a process of partitioning an image into different regions such that each region is homogeneous in nature. The level of subdivision depends on the problem being solved and segmentation stops once object of interest in the application has been isolated [13]. Image segmentation algorithms are generally based on two basic properties of intensity values: discontinuity and similarity [14]. In the first category, the approach is to perform segmentation based on abrupt changes in intensity and in second category partitioning an image into regions that are similar according to a set of predefined criteria. This technique has variety of applications including computer vision, remote sensing, image analysis, geographical information system and most widely used application is in the field of medical image processing. Medical image segmentation is an important task for identification and location of tumors, diagnosis and computer guided surgery etc [15]. Several techniques have been developed for image segmentation, but still there is need for a general solution of segmentation problem [16].

Figure. 1(a) and 1(b) represent the original brain tumor image as the input and its segmented output respectively.

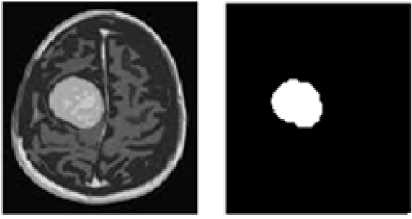
Figure. 1(a)

Figure.1(b)

To access brain structure, accurate classification of magnetic Resonance images according to tissue type at voxel level is needed. Brain tissue is usually concerned with the delineation of three types of matters White

Matter (WM), Gray Matter (GM) and Cerebrospinal Fluid (CSF). As brain structure are defined by boundaries of these tissue classes, thus accurate segmentation of these brain tissues is an important step in quantitative study. In this section we give a review of four different segmentation techniques such as: Markov Random Field (MRF), Adaptive fuzzy C - means (ASFCM), Fuzzy Connectedness (FC), Atlas based Re -fuzzy connectedness (Re-FC).

• A.    Markov Random Field (MRF)

Markov Random Field is not a segmentation method but it is a statistical model that can be used within segmentation methods. Statistical methods usually solve the segmentation problem by either assigning a class label to a pixel or by estimating the relative amounts of the various tissue types within the pixel [17]. In this paper we are considering the Markov Random Filed using Expectation maximization.

Expectation maximization (EM) algorithm [18] is a method for finding the maximum likelihood or maximum posterior (MAP) estimator of a hidden parameter with a probability distribution. EM is an iterative method which alternates between performing an expectation (E) step, in which each pixel is classified into one cluster according to the current estimates of the posterior distributions over hidden variables, and a maximization (M) step, in which the hidden parameters are re - estimated by maximizing the likelihood function, according to the current classification. These parameter -estimates are then used to determine the distribution over hidden variables in the next E step. Convergence is assured since the increase of likelihood after every iteration [19].

Markov Random Field theories are often in conjunction with statistical decision and estimation theories so as to formulate objective function in terms of established optimality principles [20]. It is a stochastic process that specifies the local characteristics of an image and is combined with the given data to reconstruct the true image. In medical Imaging, they are typically used to take into account the fact that most pixels belong to the same class as their neighboring pixels [21]. Markov Random Field are often incorporated into clustering algorithm but MAP (maximum a posterior) probability is one of the most popular statistical criteria for optimality and in fact has been the most popular choice in MRF vision modeling. By using MAP - MRF algorithm the segmentation result is robust to noise.

A difficulty associated with Markov Random Field models is a proper selection of the parameters for controlling the strength of spatial interactions [20]. Too high setting of parameter can result in an excessively smooth of segmentation result and at the same time loss of important structural details. Also, Markov Random Field method requires computationally intensive algorithms. Despite these disadvantages, MRFs are widely used not only to model segmentation classes but also to model intensity in - homogeneities that can occur in MRI images [22]

• B.    Adaptive Spatial Fuzzy C- Means (ASFCM)

This algorithm is based on fuzzy C - means that address both INU artifact and local spatial continuity. Local spatial continuity constrained is accounted by using dissimilarity index [23] that allows spatial interaction between image voxels and thus reduces the noise effect. To suppress the INU artifact, a multiplicative bias field MR Image formation model is used. By modeling the multiplicative bias field as a stack of smoothing B - spline surface an efficient two stage algorithm has been used. In the first stage the bias field is estimated slice by slice, with no explicit coupling between adjacent slices of spline surface. In the second stage , previously computed spline coefficients is updated while taking into account the explicit coupling between adjacent spline surface resulting the regularization term. Finally, the spatial continuity constraint is taken into account in fuzzy objective function [10, 24].

• C.    Fuzzy Connectedness (FC)

Anatomical objects in medical data are characterized by certain intensity level and intensity homogeneity features. The image elements seem to “hang-together” to form a certain perception of the object region. Thus, medical Image Segmentation would benefit from a method based on the “hanging togetherness” property of the object of interest. The Image Segmentation frame work based on Fuzzy Connectedness developed by J. Udupa et.al [26] effectively captures the “hanging togetherness” of image elements specified by their strength of fuzzy connectedness. Fuzzy Connectedness defines how the image elements hang together spatially in spite of their gradation of intensities. In defining objects in a given image, the strength of connectedness between every pair of image elements is considered, which in turn is determined by considering all possible connecting paths between the pair [27]. Fuzzy connectedness is constructed by combining an object -feature based and a homogeneity based affinity component in a fixed manner with various functional forms [28]. The best combination of affinity component weights for a particular functional form and particular application is determined by performing an exhaustive search.

The fuzzy Connectedness framework is resistant to some degree of intensity non - uniformity artifact in MRI. But the segmentation methods tend to be affected by severe intensity non - uniformity in MRI. Thus some intensity non - uniformity correction method is required to improve the accuracy of fuzzy connectedness method [29].

• D.    Atlas based Re-fuzzy Connectedness (FC)

To improve the limitations of Fuzzy Connectedness algorithm Atlas Based re - Fuzzy Connectedness segmentation method is used. Initially Atlas guided approach is used. These approaches are powerful tool for Medical Image Segmentation when a standard template is available. The whole idea of using the brain Atlas was to provide a prior knowledge, which can help in grouping the segments into anatomical structures. This helps to obtain fully automatic cortical segmentation procedures. The standard Atlas - guided approach treats segmentation as a registration problem [30]. Registration is a fundamental task in image processing used to match two or more pictures. Typically, one image is treated as the target image and the other is treated as a source image; the source image is transformed to match the target image. The optimization procedure is used to transform the source image based on a similarity value that evaluates the current quality of the alignment. This iterative procedure is repeated until optimum solution is found [31]. By using Atlas registration method overall position and scale differences between the atlas and the MRI is eliminated. The next step is to use fuzzy connectedness segmentation. The fuzzy connectedness method is used to segment the Magnetic Resonance Imaging for the first time and the registered atlas is utilized as an initial segmented image. While comparing the results of both Magnetic Resonance Imaging; the parameters of fuzzy connectedness can be estimated automatically and is termed as Fuzzy Connectedness -Segmented Magnetic Resonance Imaging. The third step is to adopt Parametric Bias Correction (PABIC) method to estimate and correct the Intensity non - uniformity artifacts in Magnetic Resonance Imaging. The fuzzy Connectedness segmented Magnetic Resonance Imaging is taken as the initial segmentation to initialize the parametric bias correction method and the segmented output is a parametric bias correction corrected Magnetic Resonance Imaging. The final step is a re - fuzzy connectedness segmentation method where fuzzy connectedness method is applied again, while taking the parametric bias correction corrected Magnetic Resonance Imaging as the subject, and the fuzzy connectedness segmented Magnetic Resonance Imaging as the initial segmentation.

• IV.    QUANTITATIVE METRICS FOR EVALUATION

Table I, II and III shows a comparison analysis of different segmentation algorithm related to Dice similarity coefficient, overlap ratio and Jaccard coefficient at different levels of intensity non -uniformity for brain tissue.

Intensity non - uniformity (INU) is defined as a spatially slow varying function that makes the pixels belonging to same tissue be observed with different intensity.

We have selected the following cases.

Case (I) Images with 3% noise level and 0% INU Case (II) Images with 3% noise level and 20% INU Case (III) Images with 3% noise level and 40% INU

The manually labeled images of each subject are used as gold standards and the results of each segmentation method are converted into binary images of the same voxel resolution and image dimensions as the query image. A number of volumetric and distance-based measures often used in evaluation of segmentation are computed for each segmentation result. In the following description of these measures, the segmentation result is termed as A and the gold standard is termed as G.

• A.    Dice Coefficient (D)

Dice coefficient is defined as a number of measures of the extent of spatial overlap between two binary images. It is commonly used in reporting performance of segmentation and its values range between 0 (no overlap) and 1 (perfect agreement) [32].Formula used for Dice coefficient (D) is

2|л∩ G | | А |+| G |

TABLE I. Comparison of different segmentation methods in terms of Dice Coefficient

SEGMENTATIION METHODS	WHITE MATTER	GRAY MATTER	CERE BO-SPINA L FLUID
Case I. ASFCM	0.9644	0.9587	0.9668
Case I. MRF	0.9331	0.9212	0.8503
Case I . FC	0.8331	0.8433	0.7761
Case I. Re-FC	0.8621	0.8691	0.7969
Case II. ASFCM	0.9662	0.9602	0.9667
Case II. MRF	0.9353	0.9181	0.8537
Case II . FC	0.8348	0.8467	0.7809
Case II. Re-FC	0.8709	0.8761	0.7985
Case III. ASFCM	0.9659	0.9597	0.9661
Case III. MRF	0.9313	0.9124	0.8533
Case III . FC	0.8433	0.8501	0.7746
Case III. Re-FC	0.8850	0.8832	0.8034

• B.    Overlap Ratio (OR)

Overlap ratio is used to quantify the region classified overlapping of each registration. Overlap ratio is defined as the ratio of overlapping voxels to total voxels. The relation between overlap ratio and Dice similarity coefficient is

2OR

1 + OR

TABLE III. Comparison of different segmentation methods in terms of Jaccard Coefficient

TABLE II. Co method SEGMENTATIION METHODS	parison of di s in terms of O WHITE MATTER	ferent segmen verlap Ratio GRAY MATTER	tation SEGMENTATIIO N METHODS CEREBO-	WHITE MATTER	GRAY MATTER	CEREBO-SPINAL FLUID
			SPINAL Case I. ASFCM FLUID	0.9312	0.9202	0.9357
				0.874	0.8539	0.739
Case I. ASFCM	0.9312	0.9202	Case I. MRF 0.9357
				0.833	0.8433	0.7761
Case I. MRF	0.874	0.8539	Case I . FC 0.739
				0.862	0.869	0.796
Case I . FC	0.833	0.8433	Case I. Re-FC 0.7761
				0.934	0.923	0.935
Case I. Re-FC	0.862	0.869	Case II. ASFCM 0.796
Case II. ASFCM	0.934	0.923	0.935           Case II. MRF	0.877	0.848	0.744
Case II. MRF	0.877	0.848	0.744            Case II . FC	0.834	0.846	0.780
Case II . FC	0.834	0.846	0.780           Case II. Re-FC	0.870	0.876	0.798
Case II. Re-FC	0.870	0.876	0.798           Case III. ASFCM	0.934	0.922	0.934
Case III. ASFCM	0.934	0.922	0.934            Case III. MRF	0.871	0.838	0.744
Case III. MRF	0.871	0.838	0.744             Case III . FC	0.843	0.850	0.774
Case III . FC	0.843	0.850	0.774             Case III. Re-FC	0.885	0.883	0.803
Case III. Re-FC	0.885	0.883	0.803

• C.    Jaccard Coefficient (J)

The Jaccard coefficient is another widely used overlap measure, which is very popular and used mostly as similarity indices for binary data. The area of overlap J is calculated between the original image A and its corresponding gold standard image G as shown in equation.

| A ∩ G | | A ∪ G |

Also, relation between Dice coefficient and Jaccard coefficient is related as [32]

D

- D

• V.    CONCLUSION

A great number of medical image segmentation techniques have been used for analysis of MRI human brain. In this review paper, we have presented a measure for comparing the quality of image segmentation algorithms and presented a framework in which to use it. Additionally, we have provided a comparison of four different segmentation methods which are Adaptive spatial fuzzy c - means, Markov random field, Fuzzy connectedness and Re- fuzzy connectedness in terms of Dice similarity coefficient, overlap ratio and Jaccard coefficient. The result also indicates that for same noise level and different values of intensity non-uniformity, adaptive spatial fuzzy c-means segmentation method give better result in segmentation of brain tissue.