Режимы течения топливных водоугольных суспензий в каналах распыливающих устройств

Применение водоугольных суспензий (ВУС) в качестве топлива для промышленных энергоустановок, особенно в последние годы, привлекает к ним интерес многочисленных исследователей. Большинство работ посвящено проблемам, связанным с гидродинамикой течения высококонцентрированных ВУС применительно к магистральным трубопроводным системам. Однако ряд технических трудностей, возникающих при организации внутрицехового распределения ВУС на тепловых электростанциях и, главное, при распыли-вании их через специальные форсунки в топке или аппарате предварительного отделения влаги обусловлен недостаточной изученностью параметров и режимов течения ВУС в этих условиях.

Цель работы – получение аналитических выражений, позволяющих определять геометрические размеры каналов сопел распыливающих форсунок ВУС с учетом параметров течения.

Для достижения поставленной цели проводили исследования режимов течения высококонцентрированных ВУС в тонких каналах распыливающих устройств.

Высококонцентрированная ВУС представляет собой сложную сплошную среду, свойства которой определяются такими параметрами, как влажность, зерновая характеристика исходной угольной пыли, присутствие поверхностно-активных добавок, физико-химические свойства – 243 – угля и т.д. [1–4]. В работе [5] установлены причины стабилизации водоугольных суспензий. Как показывает опыт, ВУС обладает свойствами, присущими неньютоновской жидкости степенного вида, реологическое уравнение которой имеет вид

т = ку",

где τ – касательное напряжение; γ – скорость деформации; k и n – постоянные коэффициенты, причем n < 1 [6, 7].

Зависимость (1) приводит к значительному усложнению уравнения движения ВУС по сравнению с ньютоновскими жидкостями. Однако в некоторых практических случаях движение ВУС может быть описано обычными уравнениями. При этом для конкретных технических задач необходимо учитывать реологические особенности ВУС. В качестве исходных примем уравнения динамики сплошной среды «в напряжениях» и уравнение несжимаемости, которые справедливы для любой сплошной среды:

Р

р

р

dU dt	_ дР d Р d Р = p Fx + —— + -^yx + _=L д x    д у    д z
dV dt	д P xy   д P yy   д P zy = p F +---1---1-- p у    д x   д у   д z
dW dt	c  д P xz   д P yz   д P zz = pF, +     +     + д x    8 y    д z

;

;

;

д U д V д W „ — + — +--= 0, дx дy дz где U, V, W- проекции скорости на оси координат; Pyx, Pzx, Pzy - касательные напряжения; первый подстрочный индекс обозначает ось, перпендикулярно которой ориентирована площадка, второй индекс – ось, на которую спроектировано это напряжение.

^

P = P xxx

_

P yy = P y нормальные напряжения.

^*

^P zz = ^P z

Если вязкость ц = const , то полученные уравнения носят название уравнений Стокса. Их обычно записывают в компактной векторной форме:

-

—- + (V А) = F--gradP + vA2 V;

5 t            р divV = 0,                         J где v = — - кинематическая вязкость.

P

Рассмотрим случай слоистого течения, причем скорость в продольном направлении не изменяется, а зависимость носит линейный характер. Как показывают опыты, это обстоятельство справедливо в ограниченном диапазоне скоростей, характерных для движения ВУС по трубопроводам и через регулирующую арматуру Наиболее общим видом связи между тензо-— 244 — ром напряжений Р и тензором скоростей деформации S как для изотропной, так и для анизотропной жидкости будет выражение

P = aS + b e ,

где a и b – скаляры, имеющие смысл вязкости и давления соответственно [8]. г

Анизотропность среды будет учитываться ц , который в общем случае также является тензором. Запись выражения (6) может быть использована в данной постановке задачи. Это приводит к тому, что

P xx

- P +2 ^ dU ;

8x

8V

P yy =^{- P +} 2 Щ   "

P zz

о о д W

= - P + 2 P---"

д z

P x x

= P yx

(д U д V 1 = щ 1 "

I д у д x V

P

= P zy

(д V д W

= p I +--(дz   ду

P x x

= ^РУХ

(д W д UI = щ|—+—I.

I дx    дz J

Вопрос о вязкости ВУС остается наиболее сложным. Теоретические представления, приведенные в работах [6, 9], показывают, что для жидкости, обладающей структурой, вязкость определяется из выражения

Щ(Т) = Pm + ^(Po - Щт X где μm – наименьшая вязкость предельно р азрушенной структуры; μo – наибольшая вязкость практически неразрушенной структуры; а - степень тиксотропного восстановления структуры в точке, зависящей от скорости деформации.

Чаще всего эта зависимость предст авляется линейной:

или

Щ = Po -

dU k dy

P = щ + -du ’ k dy где k - коэффициент, который зависит от структуры ВУС и внешнего воздействия - напряжения сдвига.

Последнее равенство справедливо для достаточно узкого диапазона скоростей. Для гидродинамики течения ВУС главную роль играет второе слагаемое выражений (10) и (11). Интересно отметить, что для высококонцентрированных дисперсных систем известны случаи возрастания вязкости с увеличением скорости деформации [10]. Такое различие – 245 – результатов зависит не только от содержания твердой фазы, но и от режима течения ВУС [4].

Представление μ может быть обобщено на трехмерное пространство. Однако в конечном счете можно ограничиться слоистым одномерным течением. Подставляя значения напряжений в уравнение (2), получим

a P xx  a P yx  a P zx      а ² и 2 ар а² и     Г а ² и   2 в^ А

3x   Ву   Вx     Р Вx ²     Вx Вx  ^д у²     д x Ву )

др ( д и В V А (B² W   д² и А д р (д W В и А

+II + р II +II _ ду [ ду   дx J [ дx Вz   Вz2 J  дz ( дx    Вz дP   (д2и  д2и  д2иА    д (ди дV дWА

_+ РI ++I + Р1++I + дx    ( дx2   ду2   дz2 )    дx ( дx   Ву   дz)

„ д р д и   др (д и В V А др (д W В и Ад

2+ I+ I + I+I =    + рА2 и, дx Вx   ду ( ду   дx )  дz " дx   дz Jд

так как

—»

д и д V д w _п

--+ — +--_ divV _ 0

д x    д у    д z

(в силу уравнения неразрывности),

2д^ди _д ^р (ди ₊ з к I_3p ах ax   ау ( ау ax ) az

(в силу принятого предположения о линейности μ).

Аналогичные преобразования можно провести для остальных проекций. В результате вид полученных выражений совпадает с уравнениями Стокса _—

+ (Vy^V y _ F _ 1 gradp + v A² V ^— ;

^р                                                   О³)

— divV _ О, но при этом ц определяется из выражения (8).

Как указывалось выше, практическое значение имеет слоистое течение, известное как течение Куэтта [11]. В случае ньютоновской жидкости решение имеет вид (рисунок)

a w а и А „

+I _ О ax   az )

и _

- X dP ( b 2 _ у 2 ) . 2 р dx^{x       7}

Для неньютоновской жидкости существенную роль играет зависимость ц от скорости деформации. В том случае, когда ^ возрастает с увеличением деформации пропорционально градиенту скорости, возникает добавка

U = 2/2 dPK(b ²

3 dx I

- У ²

где K – коэффициент, зависящий от структуры потока ВУС.

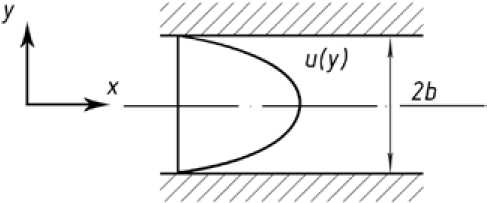
Рис. К расчету течения ньютоновской жидкости

Fig. For calculation of a current of the Newtonian liquid

Сопоставляя полученные результаты с литературными данными [7], для ламинарного потока ВУС нашли удовлетворительное соответствие. Следует отметить, что речь идет о деформации профиля скоростей.

При движении ВУС в тонких каналах, если существует зависимость (6), уравнение (15) должно быть записано в виде

dP 1   d2U                                                           (16) dx " KdUdy2; dy откуда d2U   dP dU ---= K(17) dy2      dx dy , dP          d2U dU            dU обозначая K — = K, тогда    = K "V". Если ввести = dx     1, dy2     1 dy                  dy df то, интегрируя выражение   = K 1 f, получим dy

f = cke k ,                                                                  (18) U = c i k i e* + c 2.                                                                (19)

Используя граничные условия

находим

[ ck 2 e kb + c = 0; I 1 1          2                                                                                                    (20) I c,k ,2 e - k 1 b + c, = 0, c i k shk i b = 0.                                                                       (21)

Отсюда очевидно равенство

shk1 b = 0, kib = яп , (где n = 1,2,3... )

или

dP

K—b = n n. dx

Таким образом, получено уравнение (22), в котором связаны структурный K, режимный dP и геометрический b параметры.

dx

Проведенные исследования показали, что при течении ВУС по тонким каналам необходимо учитывать неньютоновский характер ВУС. Установлено, что при движении таких жидкостей нарушается режим течения, что обусловлено взаимным влиянием структурного K, режимного dP и геометрического b параметров. Поэтому конструктивные размеры, особенно выходные dx диаметры отверстий устройств для распыливания ВУС, необходимо подбирать, учитывая полученные соотношения.

Для инженерных расчетов необходимо проводить модельные и натурные эксперименты с конкретными типами форсунок для определения структурного параметра k , зависящего от структуры потока ВУС.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда поддержки научной и научно-технической деятельности» в рамках научного проекта № 17-48-240386 р_а.