Резонансная аппроксимация спектров брэгговской структуры с дефектным слоем

Среди элементов нанофотоники, которые могут быть использованы в качестве спектральных фильтров в оптических системах различного назначения, следует выделить резонансные интерференционные фильтры на основе многослойных покрытий. Интеграция таких фильтров в спектральную аппаратуру требует решения ряда научных проблем. В частности, в изображающем спектрометре на спектральный фильтр падает излучение не только различных длин волн из широкого спектрального диапазона, но также в широком диапазоне углов падения. При таких условиях расчёт фильтра, выделяющего заданный спектральный интервал, является сложной задачей. При этом важной научной задачей является получение общего представления для пространственно-частотной передаточной функции многослойного покрытия, представляющей коэффициент пропускания спектрального фильтра как функцию угловой частоты и пространственных частот (углов падения). Данное представление позволит в общем виде описать функционирование спектрометра системы в рамках теории линейных систем.

Для спектральной фильтрации широко используются брэгговские решётки с дефектным слоем (БРДС, англ. — phase-shifted Bragg gratings) [1–4]. БРДС состоит из двух симметричных брэгговских решёток, разделённых слоем «дефекта» (рис. 1), и позволяет получить нулевое отражение и, соответственно, единичное пропускание при заданной частоте или угле падения [5]. Данный эффект имеет резонансную природу и обусловлен возбуждением мод, локализованных в слое дефекта. При этом частота, соответствующая нулевому отражению, расположена в запрещённой зоне брэгговской решётки. Такой вид спектров позволяет использовать БРДС в гиперспектральной аппаратуре, а также в системах аналоговых оптических вычислений для временного (пространственного) дифференцирования огибающей импульса (профиля падающего пучка).

В настоящей работе впервые предложена простая теоретическая аппроксимация для коэффициентов отражения и пропускания БРДС, рассматриваемых как функции угловой частоты и пространственных частот. Представленные результаты строгого моделирования спектров БРДС полностью подтверждают предложенное теоретическое описание.

Рис. 1. Геометрия задачи

Передаточная функция системы однородных слоёв

Для описания пространственных и временных преобразований световых пучков оптическими фильтрами широко используется аппарат теории линейных систем [5–9]. Передаточная функция (ПФ) линейной системы описывает отклик системы на гармонический сигнал в виде комплексной экспоненты. В оптике аналогом гармонического сигнала является плоская волна, которая характеризуется частотой, направлением распространения и направлением вектора поляризации [5].

При фиксированной поляризации ПФ системы однородных слоёв является функцией трёх аргументов: частоты и тангенциальных компонент волнового вектора падающей волны. В рамках линейной оптики указанные величины не изменяются при отражении и прохождении падающей плоской волны через многослойную структуру. При этом передаточные функции, описывающие функционирование многослойной системы в отражении и пропускании, совпадают с коэффициентами отражения и пропускания системы.

Поскольку плоская волна с произвольным вектором поляризации может быть представлена в виде суперпозиции плоских волн с ТЕ- и ТМ-поляризациями, то многослойная система может быть полностью описана коэффициентами отражения и пропускания для указанных базовых поляризаций. Пусть ось z перпендикулярна системе слоёв, тогда у волн с ТЕ-поляризацией (ТЕ-волн) вектор электрического поля перпендикулярен оси z , а у волн с ТМ-поляризацией (ТМ-волн) вектор магнитного поля перпендикулярен оси z . В явном виде выражения для ТЕ- и ТМ-волн приведены в работе [5].

Обозначим Rтетм ( kx, ky , to) и Tte,Tm ( kx, ky , to) KO-эффициенты отражения и пропускания многослойной структуры для ТЕ- и ТМ-падающих волн с частотой У и волновым вектором p = ( kx, ky, kz), где k, = -. /k,2n2m - (k2 + k2) , kn = У / c - волновое число, z 0 sup x y 0

n _sup – показатель преломления среды. Знак “–” в компоненте k_z волнового вектора показывает, что па-

обращается в ноль [3]. Отметим, что указанный ноль отражения расположен в центре первой запрещённой зоны брэгговской решётки. Нулевое отражение в центре запрещённой зоны имеет резонансную природу и связано с возбуждением мод, локализованных в дефектном

слое.

Получим представления для коэффициентов отражения и пропускания БРДС в окрестности частоты ква-зиволноводной моды, возбуждаемой в слое дефекта. Согласно (1), достаточно рассмотреть двумерный случай, соответствующий условию k_y ≡ 0. Для брэгговской структуры в окрестности нормального падения ( k_x =0) справедливы следующие аппроксимации коэффициентов отражения и пропускания как функций от k_x [10–14]:

R ( kx )

r

k ² x

-

k x ²

k z ², R

-

k p ²

, T ( k x ) = t

k

x

-

k x ²

k z ², T

-

k p ²

где r,t – нерезонансные коэффициенты отражения и пропускания, k_{z , R} , k_{z , T} – комплексные нули коэффици-

дающая волна распространяется против оси z .

Для системы однородных слоёв коэффициенты отражения и пропускания зависят только от угла между нормалью и волновым вектором, то есть коэффициенты отражения и пропускания можно рассматривать как функции только одной компоненты волнового вектора:

R T E,TM ( ^k x , ^k y , ^У ) R T E,TM ( ^^k x ^{+ k} y ,0, ^У ) , T T E,TM ( ^k x , ^k y , ^У ) = ^T T E,TM (-^ ^k x ^{+ k} y ,0, ^У ) .

ентов отражения и пропускания, k_p – комплексная константа распространения собственной моды резонансной структуры. Формулы (3) представляют коэффициенты отражения и пропускания как функцию пространственной частоты k x при фиксированной частоте to . Для простоты в (3) опущен индекс поляризации падающей волны. Чтобы получить коэффициент пропускания как функцию от двух переменных ( k x , to ), рассмотрим нули и полюсы коэффициентов отражения и пропускания как функции от to :

k^R = Zr (to), k^i = Zt (to), kp = P(to). (4)

В этом случае получим:

Резонансное представление спектров брэгговской решётки с дефектным слоем

В качестве узкополосных спектральных фильтров широко используются брэгговские решётки с дефектным слоем (БРДС) [1–4]. Такие решётки позволяют по-

лучить нулевое отражение и соответственно единичное

пропускание при k x = 2 ^П n sup sin ( 0 _O ) ^Л B

(при угле падения

00) одновременно для ТЕ- и ТМ-поляризации падающей плоской волны. Эти решётки состоят из двух симметричных брэгговских решёток, разделённых слоем дефекта. В простейшем случае слои брэгговской решётки имеют одинаковую оптическую толщину n h1= n2h2 = AB / 4, (2) где fti = ni - ns2up sin2 (00), i = 1,2, ni, hi - показатели преломления и толщины слоёв брэгговской решётки, IB - брэгговская длина волны. При оптической толщине дефектного слоя ndef hdef =%B/2, где ndef = Vnd2ef - nsup sin2 (00) , ndef - показатель преломления дефектного слоя, коэффициент отражения брэгговской решётки при длине волны XB и угле падения 00

R ( k x , to ) =

kx - Zr (to) V------------- kx - P (to),

^T ( ^kx , ^to) = ^t

k ^{2 -} Z T (^to) k x - P ( to ) .

Используя закон сохранения энергии, можно пока-

зать, что нули и полюсы связаны следующими соотношениями (см. Приложение):

Zr (to) = Re{ P (to)} ± i - Im {P (to)}, r                             (6)

Zt (to) = Re{P(to)}±ir^ Im{P(to)}.

Будем считать, что брэгговская структура содержит достаточно большое количество слоёв, а рассматриваемый интервал частот находится в запрещённой зоне брэгговской структуры. В этом случае можно считать, что нерезонансный коэффициент пропускания t равен нулю. Тогда подставляя (6) в (5) и полагая t =0, получим:

^R ( ^k x , ^to ) =

kx - Re{P(to)} r kx -P(to)

T ( kx , to) = +ir

Im { P (to)} kFP(toy.

Запишем коэффициенты пропускания и отражения при нормальном падении ( k_x =0) как функции частоты:

R ( 0, to ) = r

Re { P ( to ) }

T ( 0, to ) = ± i r

P (to) ’ Im{ P (to)}

P (to) .

Выражения (8) примут известный вид, соответствующий резонансному представлению для коэффициентов отражения и пропускания как функции частоты to [11, 15], если функцию P ( to ) разложить в ряд по to до первой степени:

P (to) = a + вto = в (to-top),

где to _p = -a / в в (9) соответствует комплексной частоте моды структуры (полюсу коэффициента пропускания и отражения) при нормальном падении ( k_x =0). Нерезонансный коэффициент пропускания ( T ( 0, to ) при | to-to_p| » 1) в (8) должен также обращаться в ноль. Данное условие выполняется при Im { в } = 0. Подставляя (9) в (7), запишем следующие аппроксимации для коэффициентов отражения и пропускания как функций ^от ( k x , ^to ) :

^R ( k x , ^to ) = r

T ( k x , ^to ) =± i r

k x² -вto+в Re { to p }

kx -P(to-top ) [3 Im {top }

k x ^-в(^to-to p )

где в e R .

В трёхмерном случае коэффициенты отражения и пропускания принимают вид:

(         \    k2 + k2 - в (to - to )

R k_x , k_y , to = r -x y '------ z ) ,

( x y )    kx + ky-e(to-top)

.         .              в Im { to p }

T (k, k , to) = ±ir —------------------,

( x y )      kx + ky-в(to-top)

где to z = Re { to p } - ноль коэффициента отражения.

.

Формулы (11) получены для некоторой фиксированной поляризации (ТЕ- или ТМ-). Из условия, что коэффициенты отражения и пропускания совпадают при нормальном падении

R Т Е ( 0, to ) = R Т М ( 0, to ) , Т Т Е ( 0, to ) = Т Т М ( 0, to ) , (12) несложно получить, что в рамках рассматриваемых аппроксимаций

^R Т Е ( k x , k y , ^to) ^R Т М ( k x , k y , ^to) , ^Т Т Е ( ^k x , ^k y , ^to) = ^Т Т М ( ^k x , ^k y , ^to) ^.

Результаты расчётов

Исследуем точность предложенных аппроксимаций (11)–(13) на примере БРДС, состоящей из двух брэггов- ских решёток с N периодами, разделённых дефектным слоем (общее число слоёв равно 4N +1). Показатели преломления материалов слоёв, дефекта, над и под решёткой определим в виде: п1 = 1,5, n 2 = 2,25, ndef = 1,5, nsub = nsup = 1. Толщины слоёв брэгговских структур определим из уравнения (2) при λB = 1500 нм.

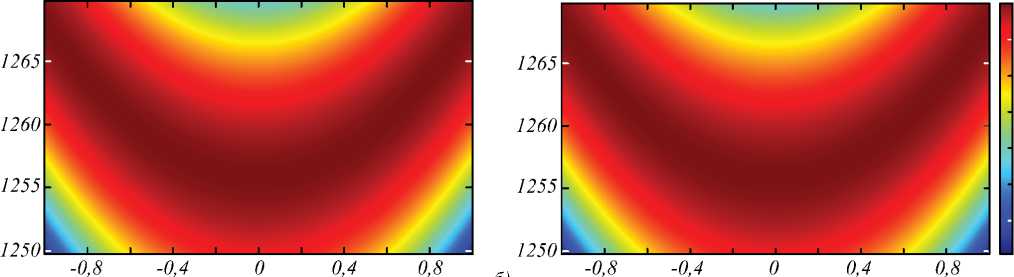
На рис. 2 а и 3 a приведены спектры коэффициентов отражения и пропускания БРДС с вышеуказанными параметрами при числе периодов N =7 и N =3. Данные спектры рассчитаны строгим методом фурье-мод [16, 17] для случая TM-поляризации и показывают наличие выраженных резонансов (минимума отражения и максимума пропускания), связанных с возбуждением в структурах квазиволноводных мод. На рис. 2 б и 3 б приведены аппроксимации коэффициентов отражения и пропускания, вычисленные по предложенной формуле (11). Сравнение рис. 2 а , 2 б и 3 а , 3 б подтверждает хорошую точность предложенных аппроксимаций. Значения относительного среднеквадратичного отклонения между строго вычисленными спектрами и их аппроксимациями, рассчитанными по формуле (11), составляют менее 10% (табл. 1). Значения параметров аппроксимирующих выражений (11), при которых были рассчитаны спектры на рис. 2 б и 3 б , приведены в табл. 2. Данные параметры были рассчитаны следующим образом. Значения комплексных частот возбуждаемых мод to p в (11) были найдены как полюсы матриц рассеяния структур при нормальном падении ( k_x =0) с использованием метода работы [18]. Нули коэффициентов отражения при нормальном падении to z соответствуют брэгговской длине волны λ_B = 1500нм. Оставшиеся значения параметров β и r были получены в результате оптимизации из условия минимума разности между коэффициентами отражения и пропускания, рассчитанными с использованием метода фурье-мод, и приближёнными выражениями (11).

Табл. 1. Относительные СКО между строго вычисленными спектрами (рис. 2а, 3а) и их аппроксимациями (рис. 2б, 3б), рассчитанными по формуле (11)

	N =3	N =7
R	10%	8%
T	7%	3,5%

Табл. 2. Параметры аппроксимаций (11)

	N =3	N =7
r	0,991864 + 2,37 - 10 - 7i	0,999889 + 5,34 - 10 - 6i
to p	1,2557677 - 1015 - 46,071064i - 1012 с - 1	1,2557677 - 1015 - 1,3828871i - 1012 с - 1
в	8,0385 - 10 - 2 + 18,872i - 10 - 4 пс/мкм2	8,0809 - 10 - 2 + 5,545i - 10 - 4 пс/мкм2

Отметим, что спектры рассматриваемых БРДС для случая ТЕ-поляризации также хорошо описываются аппроксимациями, представленными на рис. 2 б , 3 б . При этом значения относительного среднеквадратичного отклонения между строго вычисленными ТЕ-спектрами (не показаны в статье) и их аппроксимациями на рис. 2 б , 3 б составляют менее 8 %.

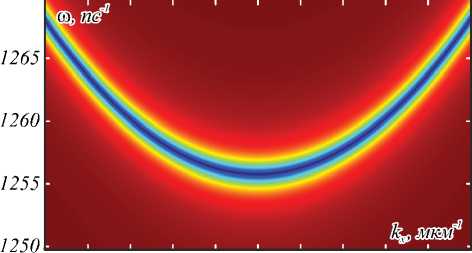
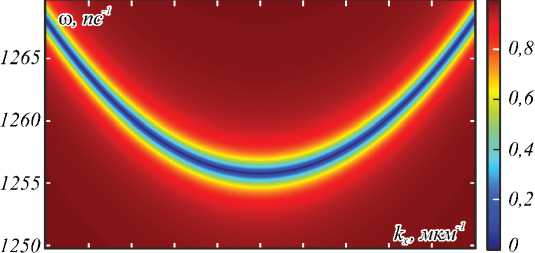
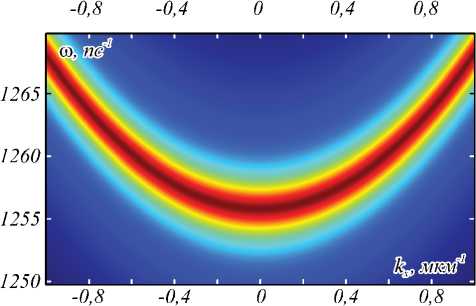
Рис. 2. Модули коэффициентов отражения R TM ( k_x, to ) (сверху) и пропускания T TM ( k_x , to ) (снизу) для БРДС, рассчитанные

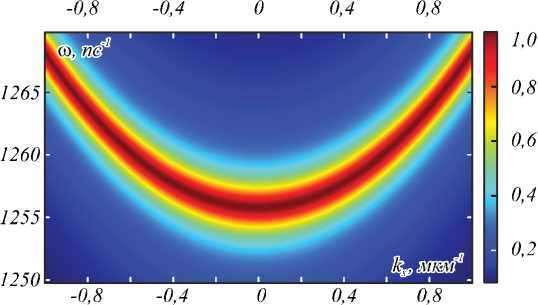
методом фурье-мод (а) и на основе резонансного приближения (11) (б) при числе периодов N = 7

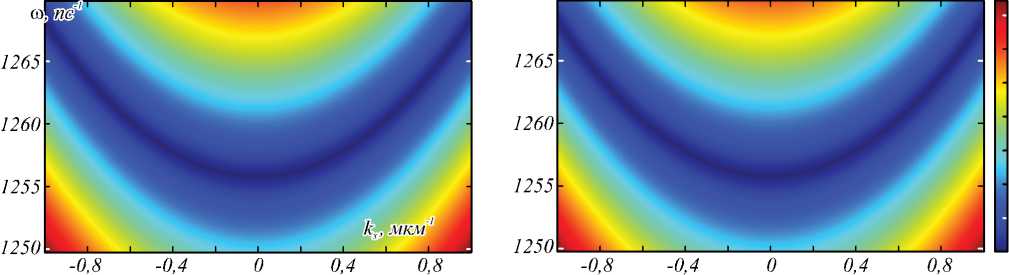
0.35 0,30 0,25 0,20 0,15 0,10 0,05 О

1,00 0,99 0,98 0,97 0,96 0,95 0,94 0,93

Рис. 3. Модули коэффициента отражения RTM (kx, to) (сверху) и пропускания TTM (kx, to) (снизу) БРДС, рассчитанные методом фурье-мод (а) и на основе резонансного приближения (11) (б) при числе периодов N = 3

Интересно отметить, что аппроксимации (11)–(13) были получены для случая, когда нерезонансный коэффициент пропускания равен нулю, то есть при большом числе периодов в брэгговской структуре. В то же время результаты расчётов, представленные на рис. 3, показывают, что предложенные аппроксимации имеют достаточно хорошую точность уже при числе периодов N = 3 (при числе слоёв 4 N + 1 = 13 ).

Заключение

В работе получена аналитическая аппроксимация коэффициентов отражения и пропускания многослойного интерференционного фильтра, основанного на брэгговской решётке с дефектом. В рамках предложенной аппроксимации коэффициенты отражения и пропускания рассматриваются как функции угловой частоты и пространственных частот (тан- генциальных компонент волнового вектора падающей волны). Приближение справедливо в окрестности собственной частоты квазиволноводной моды структуры. Результаты численного моделирования подтверждают правильность приведённого теоретического описания.

Полученные результаты позволят описать функционирование спектрального фильтра в рамках линейных систем.

Работа выполнена при поддержке гранта РНФ 1431-00014.

Приложение

Рассмотрим вид комплексных коэффициентов отражения и пропускания плоской волны, падающей на многослойную диэлектрическую структуру, обладающую горизонтальной плоскостью симметрии. Будем предполагать, что коэффициенты отражения и пропускания R и T нормированы таким образом, что квадраты их модулей соответствуют интенсивностям отражённой и прошедшей волн. Матрица рассеяния такой многослойной структуры может быть записана в виде [19]:

RT s = T R ■ (A.14)

Отметим, что коэффициенты R , T и, соответственно, матрица рассеяния в (A.14) являются функциями от ( k x , to ) . Поскольку рассматриваемая структура является диэлектрической (непоглощающей), то в силу закона сохранения энергии матрица рассеяния S является унитарной [19, 20]. Кроме того, матрица S является нормальной, и поэтому условие унитарности для неё запишется в виде |%J = |X ₂| = 1, где собственные значения матрицы рассеяния имеют вид

X 1 = R + T ; X 2 = R - T . (A.15)

Это означает, что собственные значения матрицы S должны иметь следующий вид: X 1 = e i ^ф , X 2 = e i ^и , ф , ye К . Таким образом, при фиксированных значениях ( k x , to ) комплексные коэффициенты отражения и пропускания могут быть полностью охарактеризованы двумя действительными числами ф и у .

Рассмотрим коэффициенты отражения и пропускания как функции k_x при фиксированной частоте to . Для того, чтобы коэффициенты T ( k x ) и R ( k x ) имели вид (5) рациональных функций от k_x ² , необходимо представить собственные значения (A.15) в виде рациональных функций от k_x ² с единичным модулем. Если не рассматривать вырожденные резонансы [15, 21], то для собственных значений X 1 , X 2 существуют два следующих возможных представления [21, 22]:

,      iф kx -P* (to)    [X = eiф;

1"     k 2 — P ( to ) ^; k     i_v k X - P * ( to ) (A.16)

X = eiv;                [ 2 e   kX - P(to).

Первое представление соответствует чётной ( z -симметричной) моде, второе – нечётной ( z - антисимметричной) моде [19, 22].

Подставляя (A.16) в (A.15), нетрудно получить соотношения (5), в которых r = 0,5 (ei ф + ei v), t = 0,5(eiф-eiv), а нули ZR (to), ZT (to) определяют- ся соотношениями (6).