Резонансная диагностика распределения температуры пьезоэлектролюминесцентным оптоволоконным датчиком по решению интегрального уравнения Фредгольма

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2018PNRPU MECHANICS BULLETIN

Температура – очень важная физическая характеристика состояния вещества, и определение ее числового значения представляет собой фундаментальную проблему [1–10]. Измерение температуры тел можно производить только косвенным путем, основываясь на зависимости от температуры их различных физических характеристик, которые поддаются непосредственному измерению; при этом изменение используемой характеристики должно быть связано с температурой, близкой к линейной функциональной зависимости, которая лишь незначительно искажается из-за воздействия других параметров, точно и просто воспроизводится при градуировке измерительного прибора [11]. Датчики температуры подразделяют по принципу действия, характеризующего заложенную в работу датчика некоторую известную фундаментальную зависимость информативных физико-механических характеристик чувствительного элемента датчика от изменения его температуры. В частности, термоэлектрические датчики основаны на изменении при нагреве силы тока в замкнутом двухфазном контуре, терморезистивные – на изменении сопротивления проводника, полупроводниковые – на изменении электрического напряжения на p-n-переходе, акустические – на изменении скорости звука в среде, инфракрасные пирометрические – на изменении характеристик излучения от нагретых тел, волоконно-оптические – на изменении оптических свойств световода, пьезоэлектрические – на изменении резонансной частоты пьезоэлемента от температуры. Бесконтактное измерение температуры по спектральной плотности излучения объекта в инфракрасном диапазоне с учетом статистических характеристик внешних факторов рассмотрено в [12], конструкция микроэлектронного двухпараметрического датчика для одновременного измерения давления и температуры с выделением информационных сигналов для каждого параметра из суммарного сигнала предложена в [13], резонансные пьезоэлектрические датчики обладают высокой точностью измерений в широком диапазоне температур, надежностью и долговечностью [8].

В оптоволоконных датчиках [1–7, 14–18] световод может использоваться в качестве линии передачи информативного сигнала от чувствительного элемента, который преобразует измеряемую величину в информативный параметр оптического сигнала, к устройству преобразования и обработки оптических сигналов с последующей выработкой результирующих визуальных или цифровых сигналов измерительной информации [19–23], и/или в качест- ве волоконно-оптического чувствительного элемента, способного изменять свои характеристики, в частности: фазу распространяющейся по оптическому волокну волны, поляризацию, угол вращения плоскости поляризации, коэффициенты потерь, отражения или рассеяния света под воздействием внешних диагностируемых факторов [1]. Брэгговские волоконные решетки являются одним из важнейших типов волоконно-оптических чувствительных элементов в различных современных устройствах волоконной оптики и находят применение в качестве компенсаторов дисперсии в волоконно-оптических линиях связи, зеркал волоконных и полупроводниковых лазеров, чувствительных элементов волоконно-оптических датчиков физических величин, в частности для измерения температуры, давления, опосредованно, через осевые деформации брэгговской решетки. Актуальность развития волоконнооптических систем распределенного измерения физических величин на основе длинных брэгговских решеток [24-27] обусловливается необходимостью проведения мониторинга физических полей для протяженных объектов с высоким пространственным разрешением. Принцип действия и результаты численного моделирования двухпараметрического датчика на основе брегговских решеток для одновременного измерения деформации и температуры даны в [28] на основе калибровки сигналов по шкале длин волн. Волоконно-оптическая сенсорная система с записанным массивом из 12 сенсоров из брэгговских решеток в одном волоконном световоде дана в [29], где оптическое излучение с широкополосного источника поступает на массив сенсоров и отраженный сигнал обрабатывается анализатором спектра и по положениям максимумов отражения вычисляется температура каждого сенсора; характеристики лазера позволяют опрашивать до 45 датчиков температуры в диапазоне 100 °С с погрешностью не более 1 °С. На примере волоконно-оптической измерительной сети томографического типа в [30] выполнено исследование алгебраических и нейросетевых методов реконструкции распределенных физических полей; представлены методы и результаты реконструкции функций как точечных, так и непрерывных пространственных распределений температурного поля [9, 31, 32]. В [33] рассмотрены принципы и физические пределы мультиплексирования внутрисветоводных массивов из дифракционных и интерференционных волоконно-оптических датчиков. К недостаткам волоконно-оптических датчиков температур с решетками Брэгга можно отнести их сильную зависимость от внешних воздействий. В частности, механическое воздействие на чувствительный элемент может привести к существенному искажению решетки и как следствие росту погрешности измеряемых информативных параметров и диагностируемой температуры.

Для мониторинга распределения температуры на протяженных объектах, в частности трубопроводах, широкое распространение получил распределенный оптоволоконный датчик температуры на основе комбинационного рамановского рассеяния, интенсивность стоксовой компоненты которого практически не зависит от температуры, а интенсивность антистоксовой компоненты сильно связана с температурой. В результате значение температуры определяется через отношение интенсивностей антистоксовой и стоксовой компонент; такие датчики могут работать на значительных расстояниях и с высоким пространственным разрешением, подход позволяет исключить погрешности, связанные с возможными флуктуациями мощности зондирующего лазерного импульса [15].

Известны оптоволоконные датчики с генерацией информативных световых сигналов на основе эффектов электролюминесценции или флюоресценции [34-37]. В частности, волоконно-оптический кислородный сенсор предназначен для определения содержания кислорода в жидких и газообразных средах и состоит из оптического волокна, на торец которого нанесёно специальное тонкоплёночное покрытие. Оптическое волокно сенсора передаёт излучение от светодиода к покрытию на торце оптоволокна с возбуждением в покрытии флюоресценции, которая улавливается детектором - спектрометром сенсора; интенсивность флюоресценции коррелирует с измеряемой концентрацией кислорода, проникающего из газовой или жидкой среды в плёночное покрытие. Возможность для измерения температуры предоставляет эффект зависимости параметров люминесценции или флюоресценции активной светоотдающей среды от температуры. В зависимости от типа активной среды сброс ее возбуждения может идти по различным механизмам, существенным образом зависящим от температуры. При изменении температуры могут изменяться относительные интенсивности линий флюоресценции, времена затухания люминесценции среды на разных переходах. Регистрация этих изменений позволяют судить о температуре люминесцирующей среды; изменяя состав флюоресцентного материала и длину волны излучения накачки, возбуждающего флюоресценцию, можно получать различные спектральные компоненты с различным характером температурного поведения, перекрывая тем самым различные температурные диапазоны. Измерение интенсивности люминесценции происходит одновременно на нескольких различных длинах волн, и после приёма сигналы в этих спектральных диапазонах сравниваются. Такая обработка позволяет исключить влияние паразитных нетемпературных воздействий. Другой путь ослабления влияния паразитных нетемпературных воздействий - переход от измерения интенсивности излучения люминесценции к измерению времени затухания люминесценции. Выбором типа иона активатора (обычно это ионы редкоземельных элементов или ионы металлов переходных групп) и типа матрицы можно обеспечить измерения в различных температурных диапазонах. Результирующее определение датчиком температуры осуществляется с использованием известной калибровочной кривой для зависимости времени затухания люминесценции от температуры. Отметим, что меха-нолюминесцентный эффект использован в оптоволоконном датчике давления [38] с преобразованием механической энергии воздействия в оптическое излучение; явление деформационной люминесценции [39–42] наблю- дается у различных кристаллофосфоров, при пластической деформации которых происходит движение электрически заряженных дислокаций [43, 44].

К недостаткам датчиков температуры на основе эффектов флюоресценции и люминесценции относятся малая допустимая рабочая длина световода и сложность фоторегистрирующей аппаратуры вследствие относительно малой мощности флюоресцирующего излучения. Наиболее распространенными волоконно-оптическими датчиками температуры являются датчики амплитудного типа, в которых модуляция проходящего или отраженного света при изменении температуры осуществляется за счет зависимости поглощения или отражения чувствительного элемента (кристаллы, специальные волокна и т.д.) от температуры. При создании таких волоконно-оптических датчиков чаще всего используется эффект сдвига края зоны собственного поглощения в полупроводниках от температуры. Чувствительный элемент датчика представляет се-бой пластину полупроводника, зажатую между двумя световодами: входным, по которому поступает свет от источника излучения, и выходным, соединенным другим концом с фотоприемным устройством [45].

Резонансные пьезоэлектрические датчики температуры характеризуются сравнительно большой мощностью и простотой обработки информативных выходных сигналов и основаны на зависимости резонансной частоты вибраций «резонатора» – пьезоэлектрического чувствительного элемента датчика от температуры; в настоящее время используют специально разработанные резонаторы с сильной и линейной зависимостью резонансной частоты от температуры в широком рабочем температурном диапазоне –80 °С ... +230 °С. Резонансные датчики температуры, в частности, в цифровых термометрах работают с высокой чувствительностью, разрешением и стабильностью, что делает их перспективными в использовании; дополнительное применение в конструкции датчика микропроцессоров позволяет использовать резонаторы с нелинейной зависимостью резонансной частоты от температуры, которую аппроксимируют полиноминальной зависимостью, и главным фактором при выборе резонатора становится его чувствительность [46].

Цель – разработка математической модели функционирования резонансного пьезоэлектролюминесцентного оптоволоконного датчика для диагностирования неоднородного по его длине поля температур; резонансный подход позволяет использовать для решения этой задачи конструкцию ранее предложенного датчика [20].

1.    Резонансный датчик температуры

Датчик (рис. 1) [20] представляет собой слоистое волокно, состоящее из оптоволокна 1, электролюминесцентного 2 и с радиальной поляризацией пьезоэлектрического 3, цилиндрических концентрических слоев с внутренним фотопрозрачным, в частности перфорированным или сеточным 4, и внешним 5 непрерывными управляющими электродами. Для улучшения пространственной разрешимости датчика посредством уменьшения усредняющего эффекта, вносимого датчиком в реальное диагностируемое неоднородное поле температур, целесообразно минимизировать теплопроводность всех элементов, в частности электродов 4, 5 датчика в осевом направлении. Считаем, что при нагреве график амплитудно-частотной характеристики датчика смещается по оси частоты на величину изменения резонансной частоты пропорционально изменению температуры; гармоническая составляющая электрического напряжения U на управляющих электродах 4, 5 датчика необходима для возбуждения вынужденных стационарных электроупругих осесимметричных колебаний датчика, постоянная составляющая – для настройки датчика на рабочий режим в рассматриваемом диапазоне диагностируемых температур.

и упр

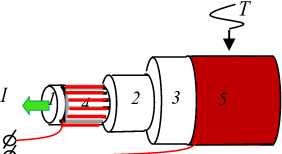
Рис. 1. Датчик температуры T с управляющим напряжением U и интенсивностью света I на выходе из световода

Fig. 1. Temperature sensor T with the control voltage U and intensity of light I at the output of the optical fiber

2.    Математическая модель диагностирования

Пусть известна амплитудно-частотная характеристика Uo (v) для электрического напряжения U на электролюминесцентном элементе фрагмента (длиной l ) датчика в зависимости от частоты ν гармонической составляющей Uw (v, t) электрического напряжения, иупр (v, t) = U0 + UуПр (v, t),               (1)

на управляющих электродах датчика при некоторой однородной номинальной температуре T , с резонансной частотой v₀, и дополнительно известна зависимость резонансной частоты v_T=v_T ( A T ) от приращения A T = T - T температуры Т , где v₀ = v_T (0) ; считаем, что при изменении температуры на ∆ T график амплитудно-частотной характеристики

U(v) - U o (v-A T )               (2)

может быть получен смещением графика U _o (v) по оси абсцисс (частоты) на величину изменения резонансной частоты

A t =v _T -v o - k _VA T ,              (3)

где k – коэффициент пропорциональности для рассматриваемого рабочего температурного диапазона датчика [46].

Амплитуда интенсивности свечения для базового случая I_o = I _o (v, l ₀) на выходе из световода рассматриваемого фрагмента длиной l и с однородной температурой T датчика с учетом прямой пропорциональности I_o = kl₀ длине фрагмента l ₀, где некоторый известный коэффициент k линейной плотности светоотдачи электролюминесцентного элемента, и заданной (при однородной светоотдаче по всей длине l датчика) линейной зависимости для «функции свечения» – зависимости интенсивности I свечения,

I = I , + k , (U - U 0 ),                (4)

от электрического напряжения U на электролюминесцентном элементе датчика в рассматриваемом диапазоне значений ( аД₀ - U ; a_xU₀ + U ), где I_o - интенсивность свечения при значении U _o = a_xU_Q ; U_o (1) - постоянная составляющая управляющего напряжения; a – управляющий передаточный коэффициент датчика [21, 22]. Таким образом, для базового случая с температурой T амплитуда свечения

1 0 ( v , I ) = y k , U 0 ( v ).                 (5)

При изменении AT температуры рассматриваемого фрагмента датчика длиной l_T « l₀ с первоначальной резонансной частотой v₀ имеем амплитуду интенсивности свечения

I_T = I o (A v , l T ) ,                       (6)

где   I_o = I _o (v, l ₀) - базовая функция (5); аргумент

A_v = v-A_T или

A_v=v- k _v A T                (7)

с учетом смещения A_T ® k _vA T (2), (3) по оси частоты.

Рассмотрим нахождение функции плотности распределения f_T ( т ) приращений температуры A T по всей длине l датчика. Интенсивность света на выходе из световода датчика

I ( v , t ) = 1 0 + 1' ( v , t )                   (8)

состоит из постоянной I _o = I _o (4) и гармонической

I’ (v, t ) = I (v) sin(to t + ф₀)                (9)

составляющих, обусловленных действием соответствующих составляющих Uo, U,упр (v, t) = Uупр sin tot с ам плитудой U^p управляющего напряжения U^ (v, t) (1) с заданной частотой v на электродах датчика, где I(v) - амплитуда гармонической составляющей интенсивности свечения I’(v, t); ф0 - начальная фаза; to = 2nv - круговая частота. Малому приращению частоты dv соответствует приращение dI(v) амплитуды интенсивности свечения I (v) на выходе из световода dI (v) = J dIт,

A T

которое получим в результате интегрирования по множеству A T значений приращений температур по всей длине l световода «локальных приращений» (6):

d I_т =

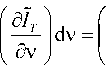
d I o ( A_v ,d I t ) 5A_V

dv на элементарных участках d l световода или dIr>1№ I  dA„61

d l_T d v

с учетом разложения функции

I o ( A v ,d l T ) « I o ( A v ,0) + P I ^{o ( A} v ’^{Г т )} )     d l T

I     ^{d l} T    J T = 0

в окрестности точки l_T = 0 в ряд Тейлора, где I_T = I _o(A, l ) (4), I _o(A_v,0) = 0 (5), d!_T = d!_T(A T ) - это некоторая малая длина участка (или суммарная длина участков) световода с приращениями температур A T g ( т , т + d т ), величина A_v =v-A_r (7). Таким образом, имеем

Г d I ( v ) = J I

<^{A T} ^

d ² 1 0 ( A v, I t ) dA_vd l_T

dL d v

с учетом (10), (11); производная амплитуды интенсивности результирующего свечения I (v) (8), (9) на выходе из световода датчика примет вид

dI (v). | dv J 'd210(Av, It ) )    d/~ I  dAvd It   J, T =0  T (13) с учетом замены d lT = dlT, (14) где lT = lT (т) - суммарная длина участков датчика с приращениями температур AT ^ т, в (12)-(14) приращение dlT обусловлено приращением dr, область значений 0 ^ lT < l, длина световода l. Приращение dlT является малой длиной участка (или суммарной длиной участков) датчика с приращениями температур

AT g (т, t + dт), которое представим в виде d/т =lfT (T)dT на основе двойного равенства dP = dlT /l = f (T)dT

K (v) S1 D(v) = k- dU0,(23)

kvk с учетом (19), (20)

OM = ( ^{5 2} 1 » ( v,¹ ) )         d U 0 A d U 0

V dvdl   J|7=o   l dU dv    ld для геометрической вероятности dP, где искомая функция плотности распределения f (т) приращений температур AT по всей длине l датчика имеет вид

т lT (т) = l J Л (т ')dT'.

-те

Вид функции следует из (15), (16); нижний предел интегрирования в (17) может быть заменен на T_min для случая, когда диагностируемые приращения температур A T g (т^_п; т_тax);   в предельных случаях имеем

К ( T_mJ = 0 , I t (t^) = l .

В результате подстановки (15) в (13) получим уравнение Фредгольма 1-го рода dI(v)     rfd2Io(Av, /T))

1--= lJ ЯЛ aT-- fT(T)dT dv      -Д   dAv5 lT   J, Ti =0

или () = lJ Q(v  kvt)fr(T)dT, dv     J —те (19) где f a2/„(v,/)) n(v) S ”(<, ) |                    (20) V dvd 1   J| 7=0 с учетом Av s v-k^AT (7) или в канонической форме те g (t) =J K (t - 5 ) f (s)ds ,(21)

-те где t = v , s S кvT , f (s) S fT (T)T=,/kv ,

K(t - s) S1 Q(t - s), g(t) S dI^t)(22)

kv для нахождения искомой функции плотности распределения f (т) приращений температур AT по длине световода через измеряемые значения производной dI / dv (19), (22) амплитуды интенсивности результирующего свечения I(v) (8), (9) на выходе из световода датчика с учетом Av = t - s (7), dT = ds / kv . Ядро Фредгольма (21) может быть выражено как через известные (заданные) амплитудно-частотные характеристики для электрического напряжения U = Uo (v) на электролюминесцентном слое датчика и коэффициенты пропорциональности k , k для вариаций резонансной частоты AT = kv AT и температуры AT (3), интенсивности светоотдачи AI = k2AU и электрического напряжения A U на электролюминесцентном слое (4) датчика в рассматриваемом рабочем температурном диапазоне.

• 3.    Численный расчет

Пусть до возбуждения колебаний в датчике действует постоянное значение электрического напряжения на электродах U _o = U _o / a_x , где U_o = 4,5 В и управляющий передаточный коэффициент а_х = 0,972 [21, 22], что обусловливает интенсивность света на выходе из световода I _o = I _o = 2,25 Вт/м², численное значение коэффициента k₇ = 1,5 А /м² в (1), (4); значения величин U _o, I_o и k соответствуют координатам серединной точки и линейной аппроксимации восходящего участка S -образной функции свечения I = I (U ) в [21, 22]. Пусть для рассматриваемой модели амплитудночастотная характеристика электрического напряжения

(               f П                   tl

^U 0 ^{( v )} = ^U a I ^{1 + cos} I T^{( v-v} 0 ) II          (25)

k      VA       JJ на электролюминесцентном элементе датчика для частотного диапазона v g (v1; v2) гармонической составляющей U^ (v, t) управляющего электрического напряжения на электродах датчика (1), ядро Фредгольма (21) (рис. 2)

^{K ( v )} = kr d U ⁰ = ^{- A} г ^sin It ^{( v-} v 0 ) I      (26)

kv dv      A VA       J с учетом (23), (25), где граничные частоты vt 2 = v0 + A, параметр A = 0,1v0,  базовая резонансная частота

k va = 200 кГц, численные значения:   A s U — =

0                                                                              a kv

= 0,1875 - 10 " ³  Вт • с • K/м²,   U = 0,25 В,   k_v = 0,01v_o =

= 2•Ю ³ (с • K) ^{- 1}.

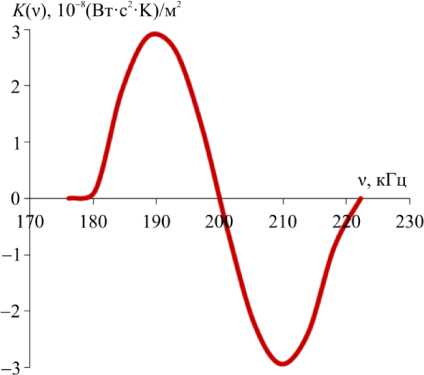
Рис. 2. Ядро Фредгольма K ( v ) в зависимости от аргумента ν

Fig. 2. Fredholm's kernel K ( v ) depending on the argument ν

На рис. 3 представлены результаты численного расчета зависимости амплитуды интенсивности результирующего свечения I (v) на выходе из световода датчика (рис. 3, а) и ее производной dI / dv (рис. 3, б) от частоты ν управляющего напряжения в отсутствие приращений температур AT = 0 и для равномерного закона распределения ∆T по длине датчика. Видно (см. рис. 3, а), что центральная резонансная частота для амплитуды интен- сивности I( v) исходящего из световода света для случая симметричного относительно нуля равномерного закона (○) распределения приращений температур ∆T по длине датчика совпадает с резонансной частотой ν для случая (AT = 0) начальной однородной температуры датчика T (  ); отрицательные приращения температур

• ( A T -< 0) смещают значение резонансной частоты влево (□), а положительные ( A T > 0) - вправо относительно

первоначального значения ν по оси абсцисс.

Пусть «искомая» функция распределения приращений температур по длине датчика задана в виде (рис. 4, а )

A T ( z ) = к е "“ z / ^l sin kz , k = пв / l ,         (27)

где координата z е (0; l) , для случая в = 1 заданы значения а = 3 (о), а = 5 (А), а = 10 (□), для случая в = 2 — значение а = 3 ( □) при к = 38 K; графики функций плотностей fT (т) для различных распределений (рис. 4, а) изображены на рис. 4, б. Обозначения графиков на рис. 4, б и, далее, на рис. 5 совпадают с соответствующими обозначениями графиков на рис. 4, а. На рис. 5 представлены результаты расчета зависимостей амплитуды I (v) (рис. 5, а) и производной dI / dv (рис. 5, б) от частоты ν управляющего напряжения для заданных реальных распределений приращений температур ∆T по длине датчика (см. рис. 4).

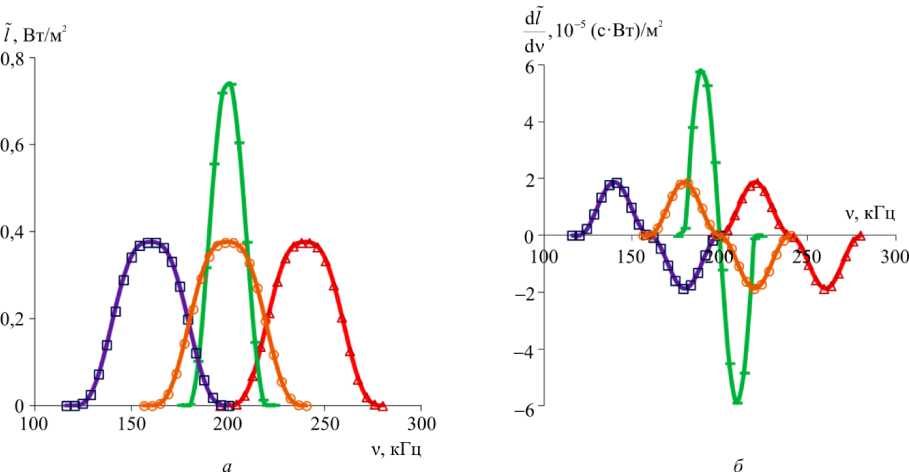
Рис. 3. Зависимости амплитуды интенсивности результирующего свечения I (v) на выходе из световода ( а )

и ее производной d I / dv ( б ) от частоты v управляющего напряжения для случая A T = 0 ( □) и для равномерного закона распределения A T на интервале ( - 10;10) (о), (10;30) (А), ( - 30; - 10) (□) по длине датчика

Fig. 3. Dependences of the amplitude of resulting luminescence intensity I (v) at the output of the optical fiber ( a )

and its derivative d I / dv ( b ) on the frequency v of control voltage for case A T = 0 (a) and for the uniform law of distribution A T on the interval ( - 10;10) (о), (10;30) (А), ( - 30; - 10) (□) on sensor’s length

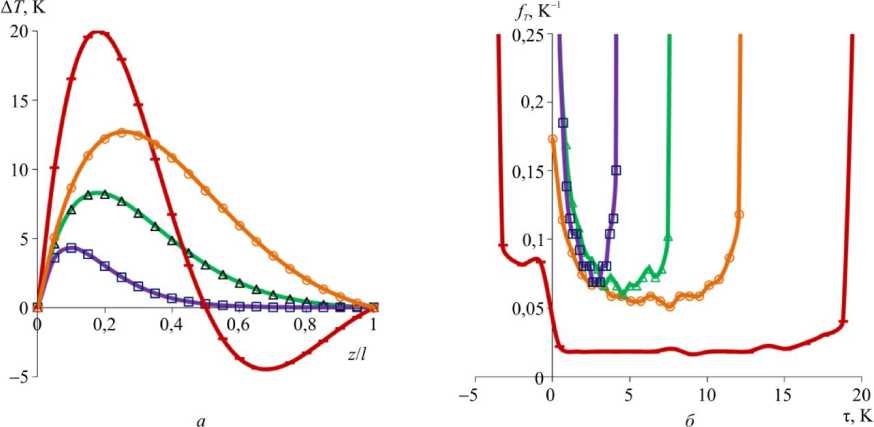
Рис. 4. Заданные распределения приращений температур A T по длине датчика ( а ) с функциями плотности f_T (т) ( б )

Fig. 4. Set distributions of increments of temperatures A T along the sensor ( a ) with functions of density f_T (т) ( b )

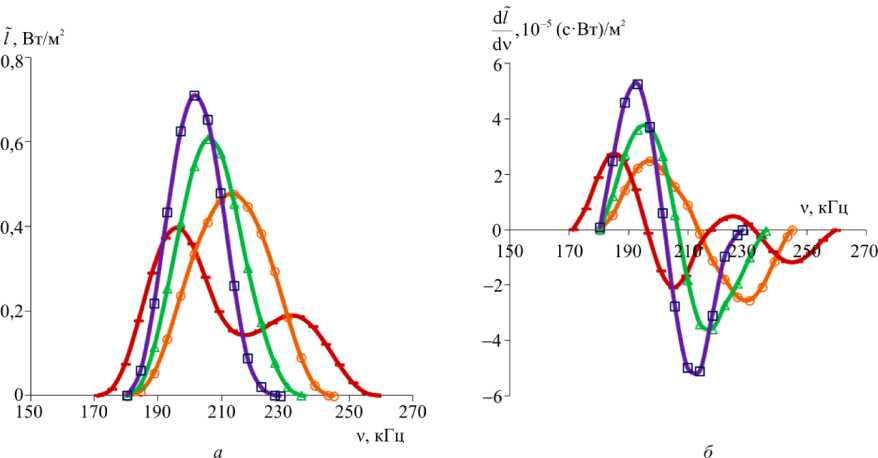
Рис. 5. Зависимости амплитуды I (v) ( а ) и ее производной d I / dv ( б ) от частоты V управляющего напряжения для заданных реальных распределений приращений температур ∆ T по длине датчика

Fig. 5. Dependences of amplitude I (v) ( a ) and its derivative d I / dv ( b ) on the frequency V of control voltage for the set real distributions of increments of temperatures ∆ T on sensor’s length

Заключение

Разработана математическая модель резонансного диагностирования неоднородного поля температур пьезоэлектролюминесцентным оптоволоконным датчиком [20] с использованием считающейся известной амплитудночастотной характеристики датчика и зависимости резонансной частоты от температуры. Считаем, что при изменении температуры график амплитудно-частотной характеристики датчика смещается по оси частоты на величину изменения резонансной частоты пропорционально изменению температуры; постоянная составляющая электрического напря- жения на управляющих электродах датчика необходима для настройки датчика на рабочий режим в рассматриваемом диапазоне диагностируемых температур, гармоническая составляющая – для возбуждения вынужденных стационарных электроупругих осесимметричных колебаний датчика. В результате искомая функция плотности распределения температуры fT (т) по длине датчика находится как решение интегрального уравнения Фредгольма 1-го рода (18)–(22) по результатам измеряемых значений производной dI / dv амплитуды интенсивности свечения I на выходе из световода по частоте ν электрического напряжения на управляющих электродах датчика; ядро Фредгольма K(t - 5) (21) рассчитывается (22) через известную амплитудно-частотную характеристику датчика и зависимость резонансной частоты от температуры (23), (24). Представлены результаты численного моделирования и изучены закономерности влияния на амплитуды интенсивности свечения I на выходе из световода различных модельных (см. рис. 3) и реальных (см. рис. 4, 5) законов распределения диагностируемых температур по длине датчика (25)-(27). Область применения датчика и рабочий диапазон диагностируемых температур, распределение которых может быть найдено из решения интегрального уравнения Фредгольма (18)–(22), определяются шириной реализуемого температурного диапазона с линейной зависимостью (3) резонансной частоты от температуры встроенного в датчик пьезо