Резонансная фокусировка лазерного света однородным диэлектрическим микроцилиндром
Автор: Козлов Дмитрий Андреевич, Котляр Виктор Викторович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 3 т.38, 2014 года.
Бесплатный доступ
В работе численно показано, что из аналитического решения задачи дифракции монохроматического непараксиального Гауссова пучка с ТЕ-поляризацией на однородном диэлектрическом (полиэстер) цилиндре при радиусах цилиндра, сравнимых с длиной волны света, можно получить фокусное пятно вне цилиндра, размер которого в 2 раза меньше дифракционного предела. Хотя радиус диэлектрического цилиндра больше длины волны всего в два раза, интенсивность в фокусе в 48 раз больше максимальной интенсивности падающего Гауссова пучка. Если всего на 2 % изменить радиус цилиндра от резонансного (для данной длины волны), то фокус увеличится в 1,5 раза, а интенсивность в фокусе будет всего в 12 раз больше интенсивности падающего света. Полученное решение соответствует росту коэффициента при функции Бесселя 18-го порядка в разложении решения для амплитуды напряжённости электрического поля в ряд по функциям Бесселя.
Фотонная наноструя, диэлектрический микроцилиндр
Короткий адрес: https://sciup.org/14059253
IDR: 14059253
Текст научной статьи Резонансная фокусировка лазерного света однородным диэлектрическим микроцилиндром
В последнее время много внимания уделяется изучению субволновой фокусировки лазерного света на микрочастицах, в том числе на микросферах и микроцилиндрах, радиусы которых сравнимы с длиной волны света [1–5]. Так, в [1–4] численно изучалась фокусировка многослойными микросферами [1], сфероидальными микросферами [2] и двухслойными микросферами [3, 4]. При этом минимальный диаметр фокусного пятна по полуспаду интенсивности был равен FWHM = 0,4 λ [2], а максимальная глубина фокуса DOF = 20 λ [3] и DOF = 22 λ [4]. В [5,6] рассматривалась фокусировка микроцилиндром: эллиптическим [5] и многослойным [6]. Минимальный размер фокуса был получен FWHM = 0,46 λ [6]. В [7, 8] моделировалась резонансная фокусировка света микросферами. В [7] с помощью диэлектрической микросферы вместе с нанометровым металлическим шариком получена резонансная фокусировка света в пятно с диаметром FWHM = 0,25 λ , а для диэлектрической микросферы получен резонансный фокус размером FWHM = 0,40 λ [8].
В данной статье рассматривается резонансная фокусировка ТЕ-поляризованного лазерного света диэлектрическим микроцилиндром. Для 18-й моды (мода шепчущей галереи) получен фокус вне микроцилиндра с размером FWHM=0,22 λ . Это меньше, чем во всех перечисленных выше работах.
Анализ аналитического решения
Аналитическое решение задачи дифракции непараксиального Гауссова пучка на бесконечно протяжённом цилиндре с круглым сечением было дано в книге [9]. В диссертации [10] данное решение обобщено для случая дифракции непараксиального Гауссова пучка, который и будет рассмотрен ниже.
Решение уравнения Гельмгольца для напряжённости электрического поля с ТЕ-поляризацией внутри цилиндра, найденное путём разделения переменных в полярных координатах, представляет собой разложение в ряд по функциям Бесселя:
E nn ( r , Ф ) = E ijb j C j J j ( knr) e Ф ,
где k – волновое число падающего излучения, n – показатель преломления цилиндра, а коэффициенты b j и C j определяются выражениями:
Cj=ω0 π×
λ (2)
r f k 2 q ^® 2
× exp - 0 - ik ( px + qy ) - ij arcsin q d q ,
4 00
-∞
Jj(z)H(j1) (z) -J′j(z)H(j1) (z) b= j Jj(nz)H(j1)′(z) -nJ′j(nz)H(j1) (z)
где z = kR , R – радиус цилиндра, p = 1 - q 2 . Выражение для числителя коэффициента можно упростить, воспользовавшись выражением для вронскиана функций Бесселя [11]:
J j ( z ) H ( j 1) ′ ( z ) - J ′ j ( z ) H ( j 1) ( z ) =
= iJ j ( z ) Y j ′ ( z ) - iJ ′ j ( z ) Y j ( z ) = i W [ J j , Y j ] = 2 i . π z
Так как при больших z функции Бесселя пропорциональны обратному корню из аргумента, а знаменатель (3) домножается на z , значение знаменателя сходится по спирали к некоторой предельной окружности в ℂ и не имеет корней. Тем не менее, для небольших j можно получить минимум в значении знаменателя, который приводит к росту одного из коэффициентов в разложении.
Для больших j минимум может не соответствовать максимальному значению коэффициента, так как значение интеграла (2) резко уменьшается с ростом j . При значениях λ, малых по сравнению с диаметром цилиндра, резонанс также не будет наблюдаться, это связанно с тем, что в выражение под интегралом (2) в качестве первого слагаемого под экспонентой входит не зависящее от диаметра цилиндра выражение, пропорциональное k 2.
Задача получения значения z, которое соответствует росту одного из коэффициентов, является нетривиальной, так как требует оптимизации на целой совокупно- сти коэффициентов. Некоторые из случаев, при которых возникает усиление коэффициентов, удалось получить подбором характеристик. В следующем разделе перечислены основные результаты и их сравнение с обыкновенной фокусировкой диэлектрическим цилиндром.
Результаты моделирования
Для двух цилиндров были подобраны значения радиусов, при которых возникает резонансная фокусировка в цилиндре, связанная с увеличением значения одного из коэффициентов разложения (1). Оба цилиндра освещались светом с одной и той же длиной волны λ, чтобы избежать влияния изменения (2). Все расчёты были выполнены на основе аналитического решения с помощью специально написанной расчётной программы.
Было обнаружено, что в диэлектрическом цилиндре с показателем преломления n = 1,59 (полиэстер) рост коэффициентов в ряде возникает при радиусе цилиндра R = 2,1749λ. В этом случае существенный вклад в распределение вносит функция Бесселя с порядком j = 18. На рис. 1, изображающем двумерное негативное распределение интенсивности в сечении цилиндра, можно отметить образовавшиеся максимумы интенсивности на краю цилиндра.
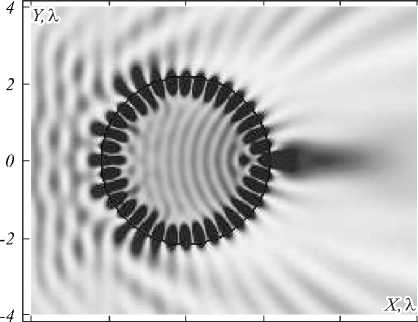
Рис. 1. Распределение интенсивности (негатив) света в сечении цилиндра (R = 2,1749λ, n = 1,59)
Распределение вдоль оси Ox (оптической оси) представлено на рис. 2, а распределение вдоль оси Oy на границе цилиндра – на рис. 3. Пунктирными вертикальными линиями отмечены границы, соответствующие дифракционному пределу для фокусного пятна. Следует заметить, что решение даёт в точке максимума интенсивность более чем в 48 раз больше, чем интенсивность падающего Гауссова пучка в перетяжке. При этом глубина фокуса по полуспаду интенсивности равна DOF=0,25λ, а ширина тоже по полуспаду интенсивности FWHM=0,22λ, что в 2 раза меньше дифракционного предела для 2D случая (FWHM=0,44λ). Площадь пятна по полуспаду в этом случае составляет всего HMA=0,05λ2.
Для сравнения было рассчитано распределение интенсивности, полученное при незначительном (около 1 %) отклонении радиуса – при R = 2,2λ. Соответствующее двумерное негативное распределение приведено на рис. 4.
Относительная интенсивность
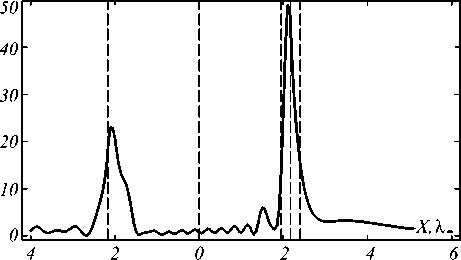
Рис. 2. Интенсивность света вдоль оптической оси Ox, по горизонтальной оси отложены длины волн
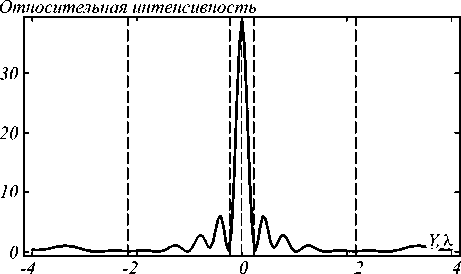
Рис. 3. Интенсивность света вдоль оси Oy за границей цилиндра x = 2,2λ; по горизонтальной оси отложены длины волн
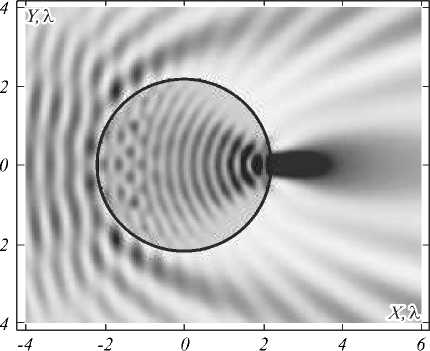
Рис. 4. Распределение интенсивности света (негатив) в сечении цилиндра (R = 2,2λ, n = 1,59)
Максимум интенсивности в этом случае только в 9 раз больше интенсивности Гауссова пучка в перетяжке, а площадь по полуспаду фокусного пятна составляет 0,31λ2. При этом отношение интегралов интенсивности по области фокусного пятна (границы пятна определяются неравенством I > Imax/2) с предыдущим случаем составляет 0,91, что равно отношению эффективностей фокусировки. Глубина фокуса равна DOF=0,8λ, что более чем в 3 раза больше, чем в предыдущем случае, а ширина фокуса равна FWHM=0,4λ, что в два раза шире фокуса на рис. 3, но немного меньше дифракционного предела. Таким образом, при n = 1,59 удаётся добиться достаточно острой фокусировки с десятипроцентной потерей эффективности по сравнению с фокусировкой почти таким же цилиндром, но на 1 % большим радиусом, для которого уже нет резонанса.
В рассмотренном случае (рис. 2) максимум интенсивности оказывался внутри цилиндра. Следует ожидать, что при уменьшении показателя преломления значение максимума будет сдвигаться от центра цилиндра. Чтобы рассмотреть случай фокусировки за поверхностью цилиндра, было получено решение для однородного цилиндра с n = 1,46 (кварцевое стекло). Усиление (резонанс) в этом случае наблюдается при радиусе цилиндра R = 2,195λ. Двумерное негативное распределение интенсивности, которое получается для этого случая, изображено на рис. 5.

Рис. 5. Распределение интенсивности (негатив) в XY-сечении цилиндра (R = 2,195λ , n = 1,46)
На рис. 6 и 7 изображены распределения вдоль Ox и Oy , из которых видно, что интенсивность в максимуме превосходит интенсивность Гауссова пучка всего в 12 раз. Глубина фокуса получившегося пятна DOF=0,8λ, ширина фокуса FWHM=0,3λ. Площадь пятна по полуспаду интенсивности HMA=0,25λ2.
Относительная интенсивность 12
О
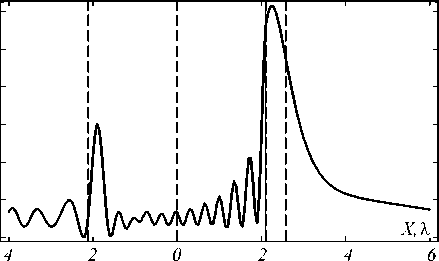
Рис. 6. Интенсивность света вдоль оптической оси Ox
При малом отклонении радиуса от резонансного R = 2,2λ (отклонению длины волны от заданной в 0,25 %), площадь фокусного пятна увеличивается до HMA=0,60λ2, интенсивность в точке максимума оказывается всего в 8 раз выше, чем интенсивность Гауссова пучка, но на 35 % увеличивается эффективность фокусировки. Также стоит отметить, что глубина фокуса возрастает с DOF = 0,8λ до DOF= 1,4λ, то есть в 1,75 раз, а ширина по полуспаду интенсивности увеличивается до FWHM = 0,4λ.
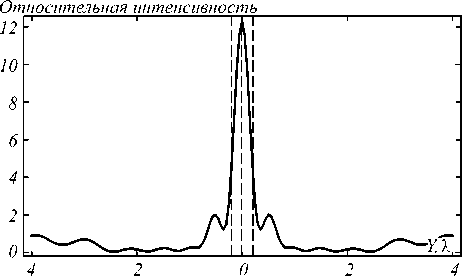
Рис. 7. Интенсивность света вдоль оси Oy в точке за поверхностью цилиндра x = 2,35
Итак, при фокусировке за поверхностью цилиндра также удаётся преодолеть дифракционный предел (FWHM = 0,3λ) и значительно уменьшить глубину фокуса за счёт потери эффективности фокусировки. Фокусировка внутри цилиндра даёт лучшие результаты по локализации фокусного пятна. При этом даже за поверхностью цилиндра ширина фокусного пятна по полуспаду интенсивности оказывается меньше дифракционного предела (FWHM=0,22λ).
Заключение
В работе численно показано, что из аналитического решения задачи дифракции монохроматического непараксиального Гауссова пучка с ТЕ-поляризацией на однородном диэлектрическом цилиндре при радиусах цилиндра, сравнимых с длиной волны света, можно получить фокусное пятно вне цилиндра, размер которого в 2 раза меньше дифракционного предела. Рассматриваемые решения соответствуют росту одного из коэффициентов в разложении решения для амплитуды напряжённости электрического поля в ряд по функциям Бесселя.
Работа выполнена при поддержке Министерства образования и науки РФ, грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и РФФИ 13-07-97008.


