Резонансная острая фокусировка света диэлектрическим цилиндром с квадратным сечением и кубом

Моды шепчущей галереи (ШГ), называемые иногда геометрическими резонансами или WGM-резонансами ( Wispering Gallery Modes Resonances ), находят применение в производстве чувствительных сенсоров [1–3], измерительных приборов [4], частотных фильтров и других оптических устройств [5], для которых основную роль играет чувствительность мод шепчущей галереи к малым отклонениям от резонансной длины волны. Моды ШГ характеризуются экстраординарными значениями добротности (Q-фактор порядка 10⁹ удаётся получить экспериментально [6]) и меньшим размером светового пятна, в которое фокусируется монохроматическое излучение при прохождении через цилиндр или сферу в условиях резонанса [7, 8]. В большинстве работ, как правило, рассматриваются моды ШГ в микрорезонаторах, позволяющих достигать высокие значения добротности: сферических [6, 9], тороидальных [10] и других. Эффекту уменьшения поперечных размеров области максимальной интенсивности на теневой стороне частиц уделено намного меньше внимания, однако он позволяет значительно увеличить разрешение пространственных оптических сенсоров за счёт уменьшения области фокусировки без усложнения технологии их производства.

Сложность представляет задача определения условий возбуждения мод ШГ. Даже для известной задачи дифракции на цилиндре значения параметров определяются только численно [11]. Поиск условий возбуждения мод ШГ в частицах с произвольной геометрией вызывает необходимость прибегать к специальным численным методам.

В данной работе были исследованы резонансные моды цилиндра с квадратным сечением при помощи FDTD-метода ( Finite Difference Time Domain method ), реализованного в MEEP, и пакета Harminv. В отличие от кругового цилиндра, цилиндр с квадратным сечением более прост в изготовлении и также фокусирует свет в область на теневой стороне цилиндра. Динамика

10.18287/2412-6179-2016-40-4-431-438.

процесса формирования WGM-резонанса была исследована с помощью FDTD-метода, реализованного в FullWAVE. С помощью FEM ( Finite Element Method ), реализованного в COMSOL Multiphysics, было показано, что эффект, схожий с эффектом возбуждения мод ШГ, может наблюдаться не только в цилиндре с квадратным сечением, но и в диэлектрическом кубе.

FDTD-моделирование резонансных мод

Моды ШГ возникают в элементах с осевой симметрией в силу многократного внутреннего отражения электромагнитного излучения внутри элемента. Одним из полезных эффектов, наблюдаемых при WGM-резонансе, является уменьшение поперечных и продольных размеров области фокусировки на теневой стороне элемента, что, например, можно обнаружить при фокусировке света сферой или круговым цилиндром. Подобный эффект можно обнаружить и в элементах с другой геометрией: в условиях резонанса излучение задерживается внутри элемента, благодаря чему после длительного облучения светом он способен излучать некоторое время в определённом диапазоне частот. Благодаря описанному выше свойству, WGM-резонансы возможно выявлять при помощи FDTD-метода. Для выявления резонанса, как правило, требуется расчёт преобразования Фурье от временной зависимости электромагнитного поля в какой-либо точке вблизи исследуемого элемента: в спектре остаточного излучения максимумы будут соответствовать резонансным частотам. Спектр остаточного излучения может быть проанализирован после облучения элемента Гауссовым импульсом, при помощи Фурье-анализа или метода диагонализации фильтра [12], который был использован в данной работе.

Инвариантность уравнений Максвелла относительно масштаба [13] позволяет связать резонансные частоты с линейными размерами исследуемого элемента и таким образом выразить их относительно длин волн. Ниже все резонансные характеристики будут приведены в масштабных параметрах соответствующего элемента – в единицах радиуса цилиндра с круглым сечением или в единицах длины стороны квадрата цилиндра с квадратным сечением. В качестве программы, реализующей FDTD-метод, использовалась программа MEEP.

Пригодность FDTD-метода для задачи определения параметров WGM-резонанса была проверена на задаче определения относительных радиусов цилиндра с круглым сечением, при которых возможно возбуждение WGM. Для диэлектрического цилиндра существует аналитическое решение задачи дифракции, поэтому параметры резонанса могут быть получены численно из аналитического решения [8].

Было проведено сравнение результатов [8] с результатами работы FDTD-метода, с помощью которого были рассчитаны радиусы цилиндра, при которых возможен резонанс. На дискретной сетке в xy -плоскости располагался цилиндр с круглым сечением радиуса R =2λ (λ – длина волны излучения) и показателем преломления n = 1,59 (полиэстер), облучаемый монохроматическим TE-поляризованным светом из точечного источника. Шаги сетки моделирования FDTD: Δ x = 0,02λ, число Куранта S = 0,5. Размер расчетной области 8λ × 8λ, ширина PML-слоёв – 0,5λ ( Perfectly Matched Layer ).

Цилиндр облучается точечным источником Гауссова импульса с несущей частотой c / λ и спектральной шириной c / λ ( c – скорость света в вакууме). После пятидесяти периодов значение z -компоненты напряжённости электрического поля регистрировалось в какой-либо точке вблизи цилиндра в течение следующих пятидесяти периодов, а полученный сигнал раскладывался на гармоники по методу диагонализации фильтра с помощью программы Harminv.

При моделировании в гармоническом разложении остаточного излучения (наблюдающегося вблизи цилиндра после прохождения импульса) могут присутствовать и нерезонансные частоты, а любые гармоники, которые были зарегистрированы вследствие особенностей положения источника или точки наблюдения, то есть они не будут наблюдаться, например, при других углах падения излучения. Чтобы увеличить точность полученных результатов, на дискретной сетке располагаются несколько точек, в которых регистрируется излучение, как представлено на рис. 1.

Из гармонического разложения зависимости остаточного излучения E z ( t ), полученного в точках вблизи цилиндра, были рассчитаны частоты мод, задерживающихся в цилиндре в двух случаях с разными расстояниями источника импульса до границы цилиндра: на расстоянии λ (рис. 1) и на границе цилиндра. Как уже было отмечено, инвариантность уравнений Максвелла позволяет связать частоты со значениями радиусов, которые обуславливают возникновение резонанса при облучении монохроматическим светом с длиной волны λ. Диаграмма значений радиуса, полученная из результатов моделирования, представлена на рис. 2.

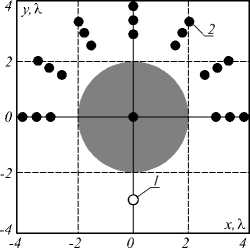
Рис. 1. Схема вычислительного эксперимента:

1 – точечный источник Гауссова импульса, 2 – точки обработки сигнала методом диагонализации фильтра

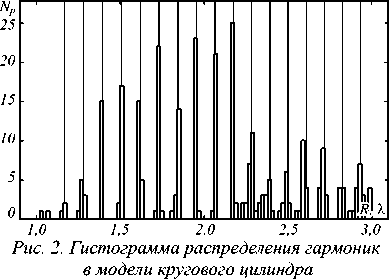
Высота столбца на гистограмме соответствует количеству точек ( N p ) вблизи границы цилиндра, в которых была зарегистрирована гармоника, соответствующая радиусу. Вертикальными линиями обозначены взятые из статьи [8] точные значения радиусов, которые обуславливают возникновение резонанса при облучении монохроматическим светом с относительной длиной волны λ. Гистограмма строилась с шагом в 0,02λ.

Можно отметить, что метод даёт хорошее согласование с результатами, рассчитанными аналитически – более восьми резонансных мод получилось воспроизвести с высокой точностью. Сравнение результатов представлено в табл. 1.

Табл. 1. Оценки для значений резонансных радиусов

Точное значение радиуса r, λ	Нижняя граница по диаграмме r min, λ	Верхняя граница по диаграмме r max , λ	Ширина интервала, λ
1,1672	1,1546	1,1680	0,0124
1,2814	1,2599	1,2986	0,0387
1,3951	1,3804	1,3997	0,0193
1,5082	1,4930	1,5142	0,0212
1,6206	1,6166	1,6247	0,0081
1,7325	1,7198	1,7407	0,0209
1,8439	1,8003	1,8456	0,0453
1,9547	1,9488	1,9617	0,0129
2,0651	2,0599	2,0713	0,0114
2,1749	2,1450	2,1950	0,0500

Резонансные моды цилиндра с квадратным сечением

Изложенный в предыдущем параграфе метод позволяет определять долгоживущие моды в любой дву- мерной и даже трёхмерной структуре с произвольной геометрией. С его помощью были рассчитаны моды диэлектрического цилиндра с квадратным сечением.

Для моделирования FDTD-методом использовались те же параметры, что и в предыдущем разделе. В качестве показателя преломления цилиндра с квадратным сечением также был выбран n = 1,59, сторона сечения цилиндра – 1,5λ.

Распространение импульса в цилиндре было промоделировано несколько раз при различных положениях источника импульса, чтобы исключить моды, которые получены вследствие особенностей положения источника и отсутствия осевой симметрии в элементе. Значения размеров стороны сечения цилиндра собраны в гистограмму на рис. 3 с помощью процедуры, описанной в предыдущем параграфе. Вертикальными линиями на гистограмме обозначены значения стороны цилиндра, при которых возникающие в цилиндре моды являются хорошо воспроизводимыми, так как были зарегистрированы четыре и более раз.

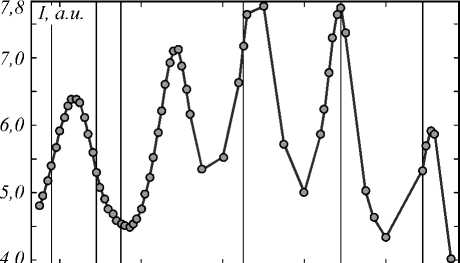
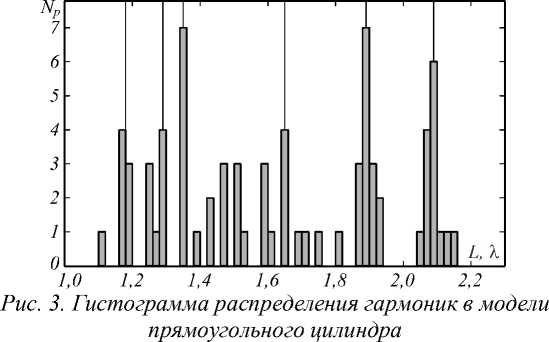
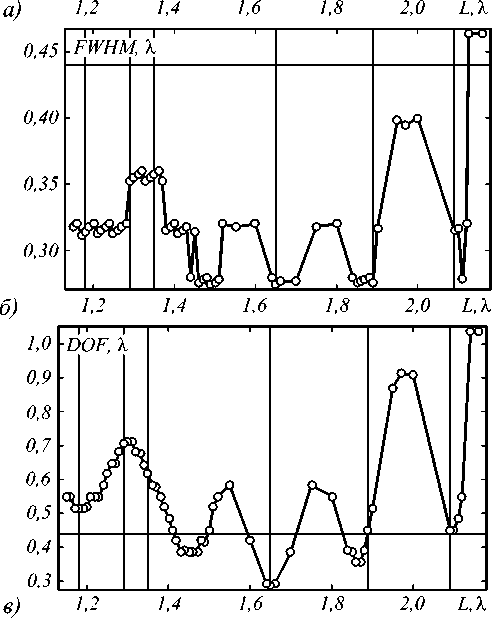
Рис. 4. Зависимость параметров фокусного пятна: максимальной интенсивности (а), ширины (б) и глубины (в) по полуспаду интенсивности, от размера стороны цилиндра

С целью определения поперечных и продольных размеров области максимальной интенсивности в фокусе I (рассчитанной как |E_z| ²) при варьировании стороны цилиндра с помощью FEM, реализованном в пакете COMSOL Multiphysics, было промоделировано распространение монохроматической волны через квадратный цилиндр. Соответствующие зависимости представлены на рис. 4–6. Вертикальными линиями обозначены резонансные параметры из рис. 3. В рассматриваемом интервале значений длины стороны сечения цилиндра (1,20– 2,09)λ во всех случаях при фокусировке света преодолевается дифракционный предел (0,44λ), который отмечен горизонтальной прямой на рис. 4 б , в .

Рис. 4 демонстрирует, что четыре из шести рассматриваемых мод представляют интерес для исследования: 1,42λ, 1,65λ, 1,89λ и 2,09λ. Однако в предыдущем параграфе для цилиндра со стороной 1,42λ не был обнаружен резонансный эффект, поэтому анализу подвергнутся только три последних случая. Во всех трёх случаях наблюдается уменьшение поперечных и продольных размеров области максимальной интенсивности, а также увеличение максимальной интенсивности в фокусе. При стороне сечения L = 1,65 λ поперечные размеры фокусного пятна были минимальными: поперечный размер FWHM =0,275λ и продольный DOF=0,289λ.

б)

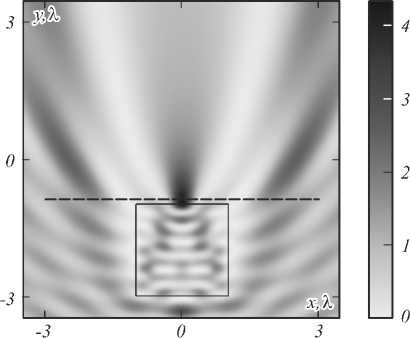
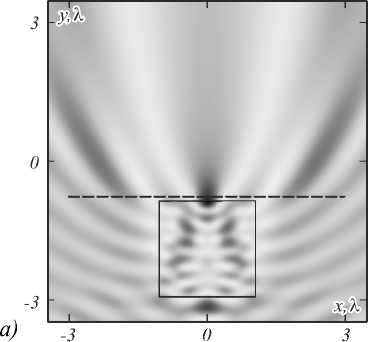
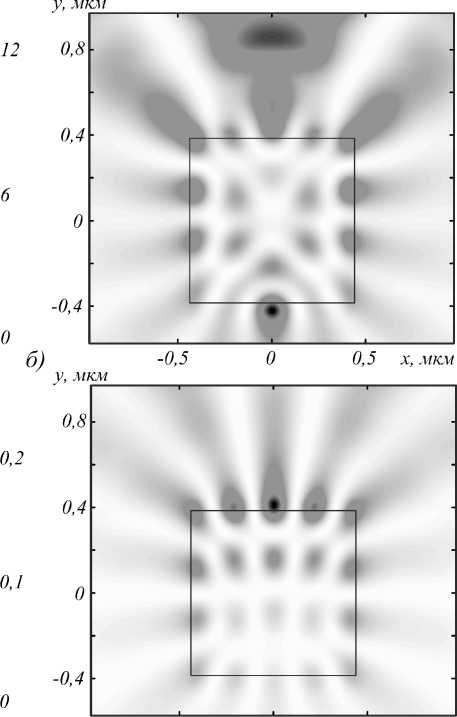
Рис. 5. Двумерное распределение интенсивности света

(негатив) в поперечном сечении цилиндра с длиной стороны L = 2,09λ (резонанс) (а) и L = 2,00λ (резонанса нет) (б)

FWHM, X

DOF, X

г) 1922 1926   1930   1934 1938

12 к

..... 05l    1 1 'A' 1 1 1 J

T

д) 1922 1926   1930   1934 1938

e)

0,1

1922 1926   1930  1934 1938

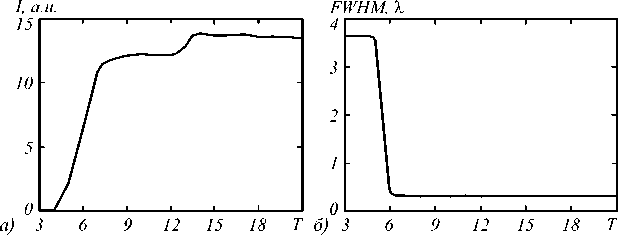
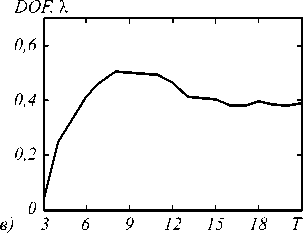
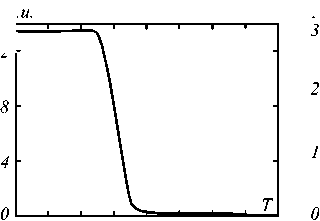
Рис. 6. Динамика изменения характеристик фокусного пятна: максимальной интенсивности (а, г), ширины (б, д) и глубины (в, е) по полуспаду интенсивности, при входе (а - в) и выходе (г - е) излучения из микроцилиндра

При стороне сечения L = 1,61 (тоже резонанс, но с меньшей добротностью, рис. 3) размеры фокуса были на 15 % больше: FWHM=0,32λ и DOF=0,42λ.

На рис. 5 представлен пример двумерного распределения интенсивности (негатив) в случае наличия и отсутствия резонанса. Параметры фокусных пятен на рис. 5 следующие: при L = 2,091 (резонанс) интенсивность в фокусе равна I max = 5,34 a.u., DOF = 0,451, FWHM = 0,321, а при L = 2,001 (нет резонанса) - I max = 4,33 a.u., DOF = 0,911, FWHM = 0,40k В случае выбора резонансного радиуса уменьшение ширины фокусного пятна происходит на 23 %. Видно, что размер фокуса в случае резонанса меньше, чем в случае его отсутствия. Но разница невелика, так как резонансные моды, возникающие в цилиндре с квадратным сечением, имеют невысокую добротность (как это будет показано в следующем разделе). Горизонтальная пунктирная линия на рис. 5 демонстрирует расстояние, на котором располагалась плоскость наблюдения. Свет с ТЕ-поляризацией на рис. 5 падает снизу вверх.

Динамика формирования резонанса в цилиндре с квадратным сечением

Проведем моделирование распространения TE-по-ляризованного импульса длительностью 1925 периодов (3,42 пс) и длиной волны λ =532 нм через микроцилиндр из полиэстра (n = 1,59) квадратного сечения с длиной стороны L =1,651 (резонанс) с помощью FDTD-метода, реализованного в пакете FullWAVE. На рис. 6 показана динамика изменения характеристик фокусного пятна. Стационарные характеристики фокусного пятна по полуспаду интенсивности составили FWHM=0,30λ (рис. 6б, д), DOF=0,38λ (рис. 6, е), а интенсивность в 13 раз превысила интенсивность падающего излучения (рис. 6а, г). Результаты, полученные с помощью FDTD-метода, согласу- ются с результатами, полученными с помощью пакета COMSOL Multiphysics и приведёнными выше.

Из рис. 6 видно, что резонанс в цилиндре устанавливается достаточно быстро (примерно за A t = 20 фс), то есть резонанс имеет невысокую добротность ( Q = ю-A t < 100). Поэтому для проверки наличия резонанса можно использовать более короткий импульс. Проведем моделирование распространения TE-по-ляризованного импульса длительностью 100 периодов (0,18 пс) и центральной длиной волны λ =532 нм через микроцилиндр из полиэстра ( n =1,59) квадратного сечения с длиной стороны L = 1,6 1 (тоже резонансная длина стороны, но с меньшей добротностью, чем L =1,65 1 ). Стационарные пространственные характеристики фокусного пятна по полуспаду интенсивности составили FWHM = 0,34 1 , DOF = 0,51 1 , а интенсивность в 9 раз превысила интенсивность падающего излучения. На рис. 7 можно наблюдать процесс выхода моды из цилиндра с длиной стороны L = 1,6 1 (излучение падает снизу вверх).

Из полученных результатов можно сделать вывод, что резонансный режим в квадратном волноводе устанавливается очень быстро (за 10–20 фс). Однако вместе с этим резонанс является низкодобротным и поэтому мало влияет на характеристики фокусного пятна: уменьшает ширину фокуса на 15 –20 %.

Резонансные моды куба

В предыдущем параграфе было продемонстрировано, что эффект, аналогичный WGM-резонансам, может быть воспроизведён в двумерных структурах, отличных от кругового цилиндра. WGM воспроизводятся и в трёхмерных элементах, таких как сферы [7]. Результат моделирования цилиндра с квадратным сечением демонстрирует, что по аналогии можно получить подобный резонанс и в трёхмерном случае.

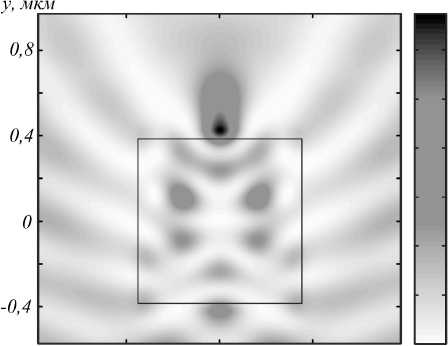
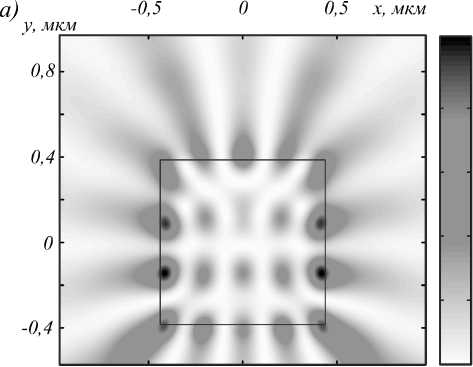
в)

Рис. 7. Распределение интенсивности в процессе выхода моды из микроцилиндра с длиной стороны L = 1,6 λ через 1850 (а), 1928 (б), 1932 (в) и 1934 (г) периодов

0,5 х, мкм

Для проверки распространение света в диэлектрическом кубе на подложке из диэлектрика с таким же показателем преломления ( n = 1,59) было промоделировано с помощью FEM реализованного в COMSOL. Шаги дискретизации метода составили λ / 10, а ширина PML-слоёв λ /3. На куб со стороной L = 2,09λ падает линейно поляризованное монохроматическое излучение, распространяющееся из подложки вдоль оси Oz , вектор напряжённости которого направлен вдоль оси Ox . Размеры получившейся области максимальной интенсивности по полуспаду составили FWHM x = 0,81λ и FWHM y = 0,45λ. Продольный размер области по полуспаду составил DOF = 0,53λ. Интенсивность света вблизи поверхности куба в 16 раз выше, чем интенсивность падающего света.

Значение L = 2,09λ было взято из результатов расчётов в предыдущем разделе для 2D-случая. Однако чтобы убедиться в том, что в данном случае наблюдается резонансный эффект, необходимо провести сравнение. При тех же параметрах сетки была промоделирована фокусировка монохроматического света на кубе со стороной L = 2,00λ. Область максимальной интенсивности, образовавшаяся в результате фокусировки, имеет следующие параметры: FWHMx = 0,73λ, FWHMy = 0,42λ, DOF = 0,30λ. Интенсивность света на границе куба превосходит интенсивность падающего света приблизительно в 389 раз, а на расстоянии 0,1λ от границы – в 18 раз. На рис. 8 представлено двумерное негативное распределение интенсивности, полученное на расстоянии 0,1λ от поверхности куба со стороной L = 2,00λ (на рис. 8 размер кадра как раз равен стороне куба). На рис. 9 изображены графики поперечных сечений интенсивности. Из рис. 8 – 9 видно, что получившееся пятно вытянуто вдоль оси поляризации. Увеличение интенсивности на границе куба свидетельствует о резонансе.

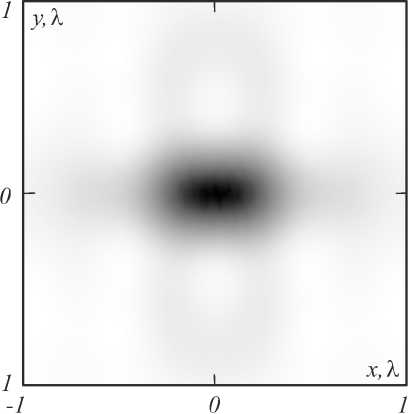
Рис. 8. Двумерное распределение интенсивности света (негатив) на расстоянии 0,1 λ от поверхности куба

I, а. и.

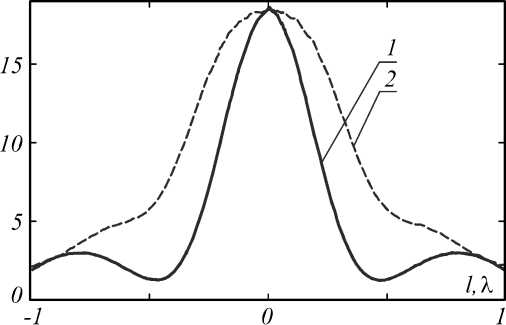
Рис. 9. Интенсивность света вдоль осей Ox (линия 1) и Oy (линия 2) двумерного распределения

Заключение

Полученные результаты позволяют говорить о геометрических резонансах, возникающих в диэлектрическом кубе на подложке и в цилиндре с квадратным сечением. Частоты резонансных мод куба, однако, не совпадают с аналогичными частотами в цилиндре с квадратным сечением. Резонанс в трёхмерном случае так же характеризуется большим усилением интенсивности на границе: интенсивность света оказалась в 389 раз выше. В то же время при фокусировке цилиндром с квадратным сечением с длиной стороны в диапазоне L = (1,2 – 2,0) λ наибольшее соотношение между интенсивностью света в максимуме и интенсивностью падающего света меньше 8.

При стороне сечения квадратного цилиндра L = 1,65λ поперечный размер фокусного пятна был минимальным и равен FWHM = 0,275λ, что почти в два раза меньше дифракционного предела в двумерном случае FWHM = 0,44λ.

С помощью FDTD-метода показана динамика формирования мод в квадратном цилиндре, аналогичная модам ШГ. Показано, что данные моды обладают низкой добротностью и поэтому мало влияют на характеристики фокусного пятна (уменьшают его на 15–20%).

В трёхмерном случае фокусировка кубом не показала значительного уменьшения размеров фокусного пятна. Поперечные размеры фокусного пятна по полуспаду интенсивности составили FWHM _x = 0,73λ и FWHM _y = 0,42λ, что на 10 % меньше, чем поперечные размеры, полученные без резонанса.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-9498.2016.9), а также грантов РФФИ 14-29-07133, 15-07-01174, 1537-20723, 15-47-02492, 16-29-11698.