Резонансные дифракционные решётки для дифференцирования оптических импульсов в отражении

Оптические элементы для дифференцирования временных оптических сигналов представляют большой интерес для широкого спектра приложений, включающего сверхбыструю оптическую обработку информации, оптические вычисления, оптическое распознавание и кодирование, формирование временных импульсов заданной формы [1, 2]. Под дифференцированием оптического импульса понимается дифференцирование огибающей импульса .

Для дифференцирования импульсов были предложены различные варианты брэгговских решёток [2–9]. При этом операция дифференцирования может быть выполнена как при пропускании, так и при отражении. Для дифференцирования при пропускании используются длиннопериодные волоконные решётки (в англоязычной литературе – long-period fiber gratings) [2–5], а также брэгговские структуры с апериодической модуляцией показателя преломления [8, 9]. Для дифференцирования при отражении используются брэгговские решётки с дефектами [6, 7]. Общим недостатком брэгговских структур является их относительно большой продольный размер, составляющий от десятков микрон до сантиметров [2–9].

В работах [10, 11] показано, что резонансные дифракционные решётки позволяют дифференцировать оптические импульсы. В [10, 11] дифференцирование осуществляется при пропускании в окрестности частот резонансов, связанных с возбуждением в решётке собственных квазиволно-водных мод. С практической точки зрения важно, что резонансные дифракционные решётки, по сравнению с брэгговскими структурами, имеют значительно меньший продольный размер (~1 микрон в ближнем ИК диапазоне). В настоящей работе впервые показано, что резонансные дифракционные решётки позволяют выполнить операцию дифференцирования оптического импульса при отражении.

Дифракция импульса на дифракционной решётке

Рассмотрим оптический импульс с центральной частотой to 0 и огибающей P ( t ), распространяющийся по оси Oz . Амплитуда импульса имеет вид:

E ( z , t ) = exp ( i k ( to ₀ ) z - i to ₀ t ) P ( t - z / v g ) =

= J G ( to-to ₀ ) exp ( i k ( to ) z - i to t ) d to ,

-7

где функция E (z, t) представляет в зависимости от поляризации x- или y-компоненту электрического поля, k(to) = Veto/с — волновое число, vg = с/Ve — групповая скорость, e — диэлектрическая проницаемость среды, G(to) — спектр огибающей импульса. Дисперсия материала в дальнейшем не учитывается. Огибающая импульса P (t) может быть представлена через спектр импульса G(to) в виде:

P ( t ) = J G ( to ) exp ( - i to t ) d to .                      (2)

-7

Соответственно, производная огибающей (2) n -го порядка имеет вид:

dnP (t)     Г , A , АП

d_? n = J G ( to )( - i to ) exp ( - i to t ) d to            (3)

-7

Пусть импульс нормально падает на дифракционную решётку (рис. 1). Огибающая отражённого импульса в 0-ом порядке дифракции имеет вид:

M

P ref ( t ) = J R ( to+to ₀ ) G ( to ) exp ( - i to t ) d to ,        (4)

-7

где R ( to ) — комплексный коэффициент отражения (комплексная амплитуда 0-го отражённого порядка дифракции) как функция частоты.

Разложив R ( to ) в ряд Тейлора в окрестности to ₀ , получим из (3), (4) огибающую отражённого импульса в виде:

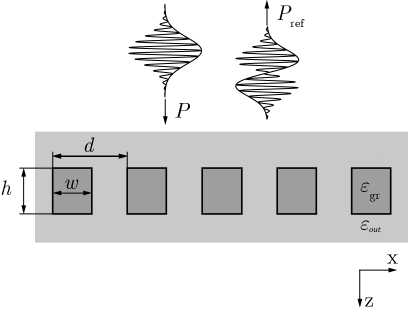
Рис. 1. Геометрия решётки

Pref (t ) = R (®0 ) P (t) + li! R '(to ) P '(t) +

+ 2 R >0 ) P"(t ) +

“ i n d ⁿR ( to )       d ⁿP ( t ) ⁽⁵⁾

S n !   d to n          d t n '

to=to 0

Формула (5) представляет огибающую отражённого импульса в виде линейной комбинации производных огибающей падающего импульса. Согласно (5), если коэффициент отражения решётки имеет вид

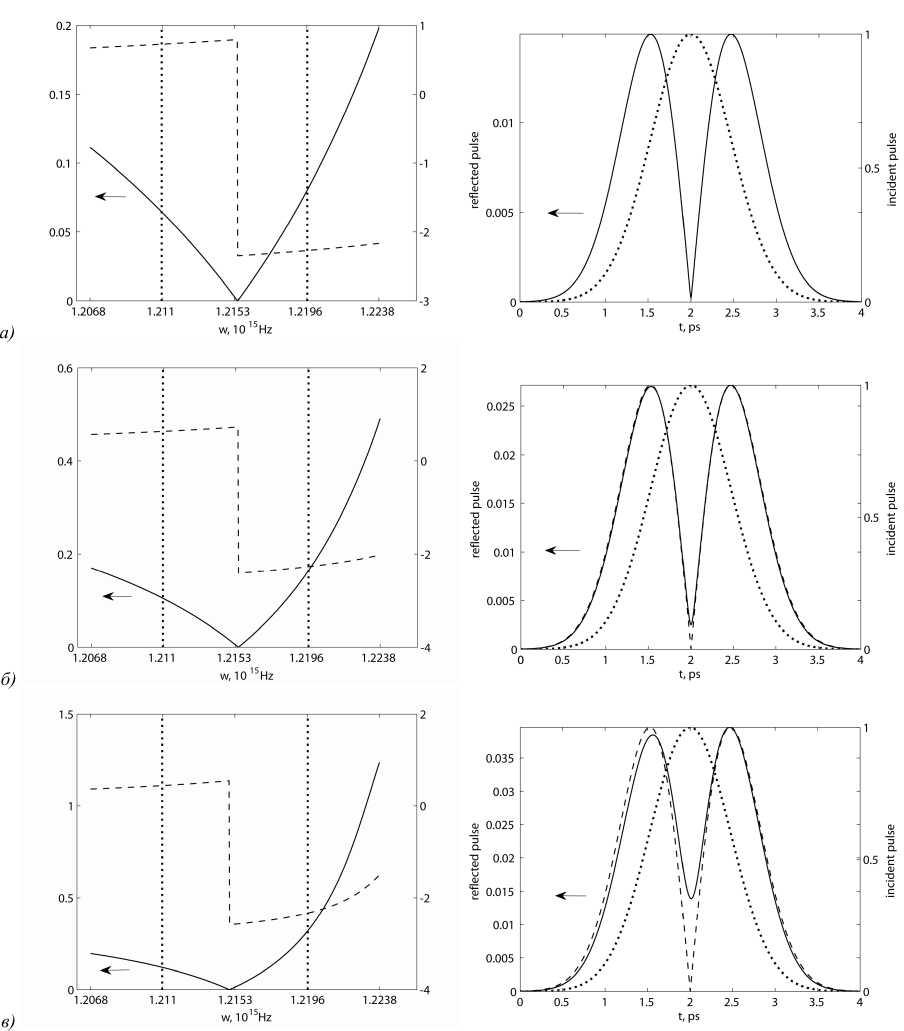
R(to) ~ -i(to-to0), |to-too|

где Q — спектральная ширина импульса, то P_ref (t) ~ P'(t), то есть решётка будет выполнять дифференцирование огибающей импульса. Определение конфигурации решётки и расчёт её параметров из условия получения отражения в виде (6) является сложной задачей, которая не может быть решена аналитически. Отметим, что функция отражения R (to) зависит от геометрических параметров дифракционной решётки, таких как период, ширина и высота ступенек и т.д.

Геометрия решётки для дифференцирования импульсов в отражении

Дифракционная решётка будет осуществлять дифференцирование огибающей, если «вес» 1-го слагаемого в (5), содержащего первую производную, будет значительно больше веса остальных слагаемых. Большая величина слагаемого с номером n = 1 достигается при резких изменениях коэффициента отражения в окрестности частоты to₀, обеспечивающих большую величину производной R'(to₀). Резкие изменения спектра отражения происходят в окрестности частот волноводных резонансов, соответствующих возбуждению в решётке собственных квазиволноводных мод [12–17]. В окрестности волноводных резонансов для комплексного коэффициента отражения справедливо следующее приближённое представление [12–14, 17]:

^R (to)

to-toR

= r —

^to-top

где r — некоторая константа (коэффициент отражения вдали от частоты резонанса), to_p— комплексная частота собственной моды структуры, toR — комплексный ноль, соответствующий полюсу top. Отметим, что в силу условия причинности Im top < 0 .

Согласно (5), (6), решётка для дифференцирования должна иметь нулевое отражение на частоте to₀. Из (7) следует, что решётка может иметь нулевое отражение в окрестности резонанса при условии toz е Ж. Это условие (условие действительности нуля в (7)) выполняется для субволновых диэлектрических решёток, симметричных в направлении распространения импульса (имеющих плоскость симметрии, параллельную плоскости решётки) [13, 17]. Простейшая дифракционная решётка такого типа показана на рис.1.

Рассмотрим субволновую диэлектрическую решётку, у которой существуют только нулевые распространяющиеся порядки дифракции. Обозначим ^Tud^(to), Ruu^(to)(^Tdu^(to), ^Rdd^(to)) Комплексные ^коэффициенты пропускания и отражения при нормальном падении волны единичной амплитуды на решётку сверху (снизу). Будем предполагать, что коэффициенты пропускания и отражения определены таким образом, что квадраты их модулей соответствуют интенсивностям дифракционных порядков при единичной амплитуде падающих волн. В окрестности волноводного резонанса коэффициенты Tud (to), Ruu (to), T_du(to), R_dd(to) имеют вид, аналогичный (7). Из соотношений взаимности [17] и из симметрии решётки в направлении распространения импульса следуют следующие равенства:

T

Tud (to) = Tdu (to) = t------z-,                          (8)

to-to

Rdd (to) = Ruu (to) = r^.                  (9)

to-to

Поскольку решётка диэлектрическая (из непоглощающего материала), то имеет место закон сохранения энергии:

| Tud (to) I1 + ^R dd (to) I₂|²+

+ 1Ruu (to) 11 + Tdu (to) 12|² = |IJ² + |I2I²,

где I1 , I2 — амплитуды падающих сверху и снизу волн. Совместно решая уравнения (8)–(10), можно получить, что для невырожденных резонансов toR е Ж и toT е Ж, то есть на некоторых частотах в окрестности резонанса коэффициенты отражения и пропускания всегда обращаются в ноль. Отметим, что если решётка не обладает симметрией в направлении распространения импульса, то выполняется только условие toT е К, в то время как ноль toR в общем случае является комплексным [13]. В случае наклонного падения условия действительности нулей toR, ®T выполняются для решёток, имеющих одновременно плоскости симметрии, параллельные плоскости решётки и перпендикулярные ей [17]. Выводы остаются верными и при отсутствии одной из двух падающих волн.

Таким образом, для дифференцирования при отражении следует использовать субволновые диэлектрические решётки, симметричные относительно направления распространения импульса. В таких решётках может быть достигнуто нулевое отражение при частоте to₀= toz. В частности, данному условию удовлетворяют дифференцирующие при отражении брэгговские решётки с дефектом, рассмотренные в работах [6, 7]. Важно отметить, что диэлектрические решётки с плоскостью симметрии, параллельной плоскости решётки, устойчивы к технологическим погрешностям в высоте решётки. Ошибки в высоте профиля такой решётки (при сохранении симметрии) приведут только к некоторому смещению нуля отражения to^R, который по-прежнему останется действительным. Это означает, что решётка будет по-прежнему дифференцировать падающий импульс, но со смещённой центральной частотой [6, 8, 18].

Расчёт дифференцирующих решёток

Рассмотрим выбор критерия оптимизации для расчёта параметров дифференцирующей решётки. Для этого оценим веса слагаемых в выходном сигнале (5). Из формул (3), (5) несложно получить следующую оценку для модуля n-ой производной:

d ⁿP (t) dtⁿ

+Q

-Q

Соответственно, в качестве оценки веса n–го слагаемого в (5), содержащего производную n-го порядка, будем использовать величину

Qn dⁿR(to) n! dton

to=to₀

В работе [11] показано, что при выполнении приближения (7) величины W_n, n > 1 образуют геометрическую прогрессию. При этом знаменатель прогрессии меньше единицы при выполнении условия | top -to₀| >Q . Последнее условие обеспечивает сходимость ряда Тейлора для R (to₀+8) при |8| < Q и, соответственно, корректность представления (5).

Для определения параметров дифракционной решётки, формирующей первую производную, предлагается использовать следующий критерий оптимизации:

и

Wo + Е Wn 1 у =---—— •--=

X(p)     w1    w?

Wo+(W2^-1- w ) W^

min,

где p — вектор оптимизируемых параметров дифракционной решётки, у>0 — некоторая константа. В частности, для решётки на рис.1 p = (d, w, h), где d — период решётки, w и h — ширина и высота ступеньки. Критерий (13) представляет собой произведение двух сомножителей. Первый сомножитель отвечает за качество дифференцирования. Его минимизация соответствует максимизации в (5) веса W1 слагаемого с номером n=1 относительно суммы весов всех остальных слагаемых. При этом, как следует из (13), достаточно максимизировать вес W₁ только относительно весов W₀, W₂. В работе [10] показано, что улучшение качества дифференцирования влечёт уменьшение амплитуды отражённого сигнала. Второй сомножитель в (13) отвечает за максимизацию амплитуды (энергии) отражённого сигнала. При этом параметр у определяет соотношение между качеством дифференцирования и энергией отражённого сигнала. Поскольку в (13) отсутствует явная зависимость от формы огибающей импульса, рассчитанная по этому критерию решётка будет выполнять дифференцирование огибающей отражённого импульса любой формы при условии, что спектр огибающей лежит в пределах определённого спектрального интервала [11].

В качестве примера была рассчитана решётка на рис. 1 для дифференцирования TM-поляризованных импульсов с центральной частотой too=1,21534O¹⁵c^-1 (Х₀=1550нм) и спектральной шириной Q=4,25•10¹²с"¹. Для диэлектрических проницаемостей материалов использовались следующие значения: εgr=5,5 (материал решётки), εout=2,1 (материал над решёткой, под решёткой и в щелях решётки). Указанные значения соответствуют материалам типа феррит-гранат и кварц. Расчёт геометрических параметров решётки проводился на основе оптимизации по критерию (13) при у=0 с использованием метода последовательного квадратичного программирования [19]. При этом для расчёта спектров отражения R(to) использовался метод фурье-мод в формулировке работ [20–23]. Полученные в результате оптимизации параметры решётки указаны в подписи к рис. 2.

В левой колонке рис. 2а показаны модуль (непрерывная линия) и аргумент (пунктирная линия) коэффициента отражения R(to) рассчитанной решётки. Согласно рис. 2а, левая колонка, в пределах указанного интервала частот комплексный коэффициент отражения решётки с высокой точностью соответствует функции дифференцирующего фильтра ^Rdiff (^to) ~ ^-1(^to-to0) .

Рис. 2 . Левая колонка: модуль (непрерывная линия) и аргумент (пунктирная линия) коэффициента отражения решётки.

Вертикальным пунктиром отмечен использованный в расчёте спектральный интервал | to — to₀1 < Q, Q = 4,25 • 101² c^—1

Правая колонка: Модуль амплитуды огибающей отражённого сигнала (непрерывная линия), модуль аналитически рассчитанной производной (пунктирная линия) и огибающая падающего импульса (точечная линия, шкала справа). Параметры решёток и коэффициенты корреляции (r): (a) d = 1040 нм, h = 610 нм, w = 760 нм ; r= 0,9999

• (б)    d = 1050 нм, h = 590 нм, w = 810 нм ; r = 0,9995

• (в)    d = 1060 нм, h = 570 нм, w = 780 нм ; r=0,9853

В правой колонке на рис. 2а представлен пример работы решётки при падающем импульсе с гауссовской формой огибающей P (t ) = exp(—t2 / 2a2), где σ=0,471 пс. Непрерывной линией показан модуль амплитуды огибающей импульса, отражённого от рассчитанной решётки, пунктирной линией — мо- дуль аналитически вычисленной производной и точечной линией — огибающая падающего импульса. Модуль аналитически вычисленной производной на рис. 2а в правой колонке привёден с масштабным коэффициентом, обеспечивающим равенство максимальных значений модулей аналитической производной и огибающей отражённого импульса. Для характеристики меры близости модулей аналитической производной и огибающей отражённого импульса будем использовать выборочный коэффициент корреляции [24]. Для графиков на рис. 2а, правая колонка, выборочный коэффициент корреляции равен 0,9999. Напомним, что рассматриваемая решётка была рассчитана при γ=0 в (13), то есть из условия максимума качества дифференцирования. При этом максимальная амплитуда отражённого сигнала составляет всего 1,5% от максимальной амплитуды падающего импульса.

Увеличивая параметр γ в (13), можно рассчитывать решётки, обеспечивающие большую величину амплитуды огибающей отражённого импульса, но при худшем качестве дифференцирования. В качестве примера на рис. 2б, в представлены модули и фазы коэффициентов отражения решёток, рассчитанных при двух возрастающих значениях параметра γ (γ=0,2 и γ=0,3, соответственно). Параметры решёток указаны в подписи к рисунку. В правой колонке на рис. 2б, в представлены расчётные амплитуды импульсов, отражённых от указанных решёток. В качестве падающего импульса использовался импульс с вышеуказанными параметрами. Рисунки 2б, в показывают увеличение амплитуды отражённого сигнала при одновременном снижении качества дифференцирования.

Заключение

Показано, что для дифференцирования оптических импульсов при отражении следует использовать резонансные субволновые диэлектрические решётки с плоскостью симметрии, параллельной плоскости решётки. Получен критерий оптимизации для расчёта параметров дифференцирующей решётки. С использованием указанного критерия рассчитаны резонансные решётки для дифференцирования пикосекундных импульсов при отражении. Рассчитанные дифракционные решётки обеспечивают различные соотношения между точностью дифференцирования и амплитудой (энергией) отражённого импульса. Результаты моделирования дифракции пикосекундного импульса с гауссовской огибающей по времени на рассчитанных резонансных решётках показывают высокую точность дифференцирования. Значение коэффициента корреляции между модулем аналитической производной и огибающей отражённого импульса может превышать 0,999. При этом максимальная амплитуда отражённого импульса составляет 1,5–2,5% от максимальной амплитуды падающего импульса.

Работа выполнена при поддержке государственного контракта 07.514.11.4060 и грантов РФФИ 1207-00495, 11-07-00153, 11-07-12036.