Резонансные магнитооптические эффекты в дифракционных решетках с намагниченным слоем

В настоящее время большое внимание уделяется эффекту экстраординарного пропускания (extraordinary optical transmission), состоящему в резонансном увеличении интенсивности света, проходящего через дифракционную решетку. Данным эффектом обладают дифракционные решетки, изготовленные из материалов с высокой проводимостью (серебро, золото) [1-5].

Целью данной работы является исследование магнитооптических свойств двумерных структур, содержащих одну или две дифракционные решетки, обладающие эффектом экстраординарного пропускания, и равномерно намагниченный слой. Мотивом для данного исследования явилось следующее. Дифракционные решетки традиционно используются для возбуждения мод в плоскопараллельном волноводе. Волноводное распространение излучения в намагниченном слое может привести к усилению эффектов Фарадея и Керра, состоящих в повороте плоскости поляризации в прошедшей и отраженной волнах. Таким образом, указанные структуры могут обладать как свойством резонансного пропускания, так и эффектом резонансного вращения плоскости поляризации.

В работах [6, 7] рассмотрены решетки из ферромагнитного материала, однако усиления эффектов Фарадея и Керра в них не обнаружено. В работах [8, 9] рассмотрена двухслойная структура, содержащая трехмерную бинарную дифракционную решетку из золота и намагниченный слой. В [8, 9] показано, что такая структура позволяет при коэффициенте пропускания в 3540% увеличить на порядок угол вращения плоскости поляризации в прошедшей волне (угол Фарадея) по сравнению с однородным намагниченным слоем.

В данной работе впервые исследована двухслойная система, содержащая двумерную дифракционную решетку и намагниченный слой. Показано, что система с двумерной решеткой также обладает резонансами пропускания и позволяет при коэффициенте пропускания в 40% увеличить угол Фарадея в 5 раз. В качестве обобщения рассмотрена симметрич- ная трехслойная структура, получаемая путем добавления второй дифракционной решетки под магнитный слой. Показано, что переход к трехслойной структуре позволяет при коэффициенте пропускания в 46% увеличить угол Фарадея в 17 раз.

Геометрия системы и параметры задачи дифракции для двухслойной структуры

Геометрия исследуемой двухслойной структуры показана на рис. 1. Верхний слой представляет собой бинарную дифракционную решётку из золота. Нижний слой – это равномерно намагниченная пластинка, вектор намагниченности которой направлен по нормали к поверхности.

к

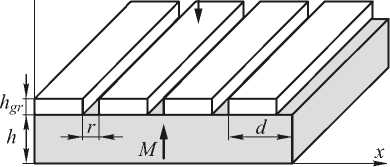
Рис. 1. Геометрия двухслойной системы, содержащей бинарную дифракционную решетку и магнитный слой

Для моделирования дифракции электромагнитной волны на данной структуре использовался метод связанных волн (rigorous coupled-wave analysis) [10-15]. Данный метод решения уравнений Максвелла является разновидностью дифференциального метода и занимает лидирующие позиции по функциональным возможностям и широте использования. Решение задачи дифракции было основано на устойчивом алгоритме, предложенном в [11]. Дополнительно, при определении поля в каждом слое, использовались специальные правила для разложения в ряд Фурье произведения функций [12-15]. Применение этих правил позволяет достичь лучшей точности представления компонент электромагнитного поля отрезками рядов Фурье и является осо- бенно актуальным при решении задачи дифракции на решетках, изготовленных из материалов с высокой проводимостью.

В области решетки диэлектрическая проницаемость является периодической функцией

^s( x ) =

1, X ^G [ 0, r ) , ^s gr , x e^[ r , d ) ,

где d – период решетки, r – размер отверстия. Диэлектрическая проницаемость магнитной пластинки описывается тензором [16]

^S m

s

- ig cos 9 ig sin 9 sin ф

ig cos 9

s

- ig sin 9 cos ф

- ig sin 9 sin ф ig sin 9 cos ф

s

, (2)

где s - главная диэлектрическая проницаемость среды, g – величина, характеризующая намагниченность среды, 9 и ф - углы сферической системы

координат, описывающие направление вектора намагниченности. В случае, когда вектор намагниченности направлен по нормали к поверхности (полярная геометрия), 9 = 0, ф = л/2 и формула (2) при-

нимает вид:

s

s

m

^- ig

ig

s

0 s

проницаемости материала решетки е _gr = ( 2 ) использовались справочные данные для золота [17]. В частности, при 2 = 883,7нм е _gr =-31,17 + 1?94 i .. Для магнитного слоя использовались параметры е = 5,5 + 0,0025 i , g = ( 1 - 0,15 i ) х 10 ^{- 2}. Эти параметры соответствуют материалу Bi:YIG (железоиттриевый гранат, допированный висмутом), который является одним из наиболее распространенных материалов магнитооптики [18]. График пропускания на рис. 2 имеет резкий пик в 40% при длине волны 2 = 883,7 нм, который совпадает с отрицательным пиком угла Фарадея. Значение угла Фарадея в пике составляет -2,25 градуса, что почти в 5 раз больше, чем просто для магнитной пластинки, помещенной в оптически согласованную среду (в среду с такой же диэлектрической проницаемостью е = 5,5 + 0,0025 i ,). Отметим, что параметр эллиптичности составляет всего 0,53 градуса.

На рис. 3 представлены расчетные графики пропускания и угла Фарадея от толщины пластинки при длине волны 2 = 883,7 нм и вышеуказанных параметрах. Графики на рис. 3 показывают ряд пиков пропускания и ряд отрицательных и положительных пиков угла Фарадея. Пики пропускания на рис. 2, 3 по-видимому связаны с явлением экстраординарного пропускания, свойственного решеткам из хороших проводников.

Магнитная проницаемость считалась везде равной единице [16].

Результаты исследования двухслойной структуры

На рис. 2 представлены расчетные графики коэффициента пропускания и угла Фарадея в зависимости от длины волны. Угол Фарадея соответствует углу между большой осью эллипса поляризации для волны в нулевом прошедшем порядке дифракции и осью OX .

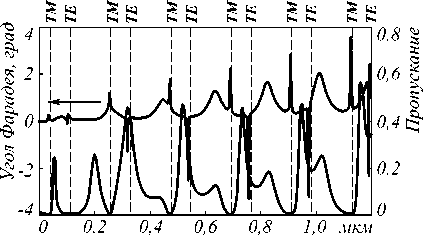
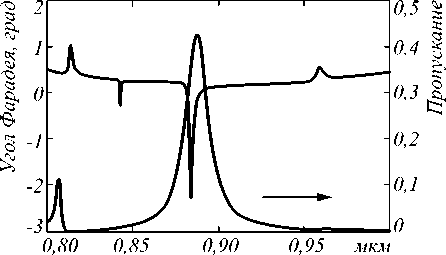
Рис. 2. Пропускание (точечная линия) и угол Фарадея (сплошная линия) в зависимости от длины волны

Графики на рис. 2 получены при нормальном падении волны с ТМ-поляризацией (вектор Н параллелен штрихам решетки) при следующих геометрических параметрах: период d = 750 нм, ширина отверстия r = 75 нм, толщина решетки h_gr =75 нм, толщина магнитного слоя h =537 нм. В качестве диэлектрической

Рис. 3. Пропускание и угол Фарадея в зависимости от толщины намагниченного слоя при нормальном падении волны. Вертикальные линии обозначают толщины возбуждения мод

Пики угла Фарадея могут быть обусловлены увеличением оптического пути света в намагниченном слое вследствие возбуждения дифракционной решеткой мод и волноводного распространения излучения в слое. Для проверки гипотезы о связи резонансов угла Фарадея с волноводным распространением излучения в слое найдем оценки толщин магнитного слоя, при которых в нем будут возбуждаться моды. Для простоты расчетов пренебрежем магнитной составляющей, и будем считать g=0. Возможные направления распространения мод в слое будем считать совпадающими с направлениями распространяющихся дифракционных порядков решетки. При этом возможные углы между направлениями мод в пластинке и нормалью к пластинке определяются по формуле решетки

6 i = arcsin ( i X / n f d ) ,

где n f = Ve - показатель преломления слоя. Усло-

вие возбуждения моды имеет вид [19]:

2 k 0 n f cos ( ⁶ i ) h m ^-ф c ^-ф , = 2 П m ,             (5)

где k 0 = 2 п / X , h_m - толщина пленки, m e Z - по

рядок моды, ф _c и ф ^ - набеги фаз, возникающие

при отражении моды от верхней и нижней границ слоя, соответственно. Значения ф ^ зависят от поля-

ризации и находятся из формул Френеля на границе диэлектрик-воздух. Поскольку размер отверстий в решетке составляет всего 10% от величины периода, то оценка значений ф ^ также может быть получена

из формул Френеля на границе диэлектрик-золото.

При указанных параметрах решетки распространяющимися порядками, способными возбудить моды, являются ±1 порядки дифракции. Поэтому в качестве угла распространения в (5) выберем угол 6 1 = 30,16 ° , соответствующий ±1 порядкам. В этом

случае толщины определяются по формуле

h = 2 ^п m + ^ф c + ^ф , ^m 2 k ₀ nj cos ( 6 1 )

Расчетные значения толщин (6), при которых в слое распространяются ТЕ- и ТМ-моды, приведены в таблице 1.

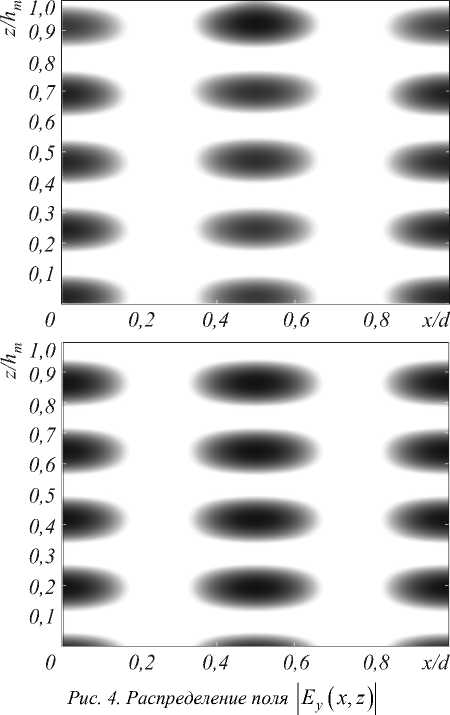
в намагниченном слое с толщиной 974 нм (сверху) и в идеальном диэлектрическом волноводе (снизу)

Таблица 1. Толщины, при которых в слое распространяются моды

Порядок	h m	h m
моды m	для ТЕ мод (нм)	для ТМ-мод (нм)
0	111,9	39,9
1	329,8	257,8
2	547,7	475,8
3	765,6	693,7
4	983,5	911,6
5	1201,4	1129,5

Для сравнения на рис. 4 снизу показано распределение поля в волноводе [19]

| E y ⁽ x , z )|

cos ( в x ) •

cos ( k f Z

-— sin k_f

(kfz)

, (7)

где

в = k ₀ n f sin 6 1

Y c =V^e 2 - ^k 02 ^e gr ,

Полученные значения отмечены на рис. 3 вертикальными пунктирными линиями. Из рисунка 3 видно, что толщины h_m^TE хорошо совпадают с положением отрицательных пиков угла Фарадея, а толщины h_m^TM – с положением положительных пиков. При этом положительные максимумы угла Фарадея также совпадают с минимумами пропускания. Интересно сравнить распределение поля в области намагниченного слоя с полем ТЕ-моды соответствующего диэлектрического волновода. Для ТЕ-моды электрическое поле содержит только компоненту E y ( x, z ). На рис. 4 сверху приведено распределение поля \Е_у ( x , z )|, рассчитанное в намагниченном слое при толщине слоя 974 нм. Указанное значение толщины слоя соответствует отрицательному пику угла Фарадея на рис. 3 и близко к оценке h 4 = 983,5 нм , полученной по формуле (6).

kf = ^ k 2 n 2 — в ² . Поле (7) соответствует суперпози-

ции двух мод, распространяющихся в направлениях +1 и -1 порядков решетки. Рисунок 4 показывает, что компонента поля E y ( x , z ) в намагниченном слое имеет выраженный модовый характер и близка, с точностью до сдвига по оси z , к оценке поля в волноводе (7). Аналогичную модовую структуру компонента поля E y ( x , z ) имеет и при других тол-

щинах, соответствующих отрицательным пикам угла Фарадея. Для положительных пиков углов Фарадея выраженную модовую структуру имеет компонента поля H y ( x , z ) . При этом модовая структура компонент E y ( x , z ) , H y ( x , z ) быстро пропадает при удалении от пиков угла Фарадея. Таким образом, проведенные расчеты подтверждают связь пиков углов Фарадея с волноводным распространением излучения в намагниченном слое.

Предлагается следующее качественное объяснение резонансов угла Фарадея. При падающей волне с ТМ-поляризацией вращение плоскости поляризации и появление ТЕ-компоненты обусловлено наличием намагниченного слоя в рассматриваемой двухслойной системе. Максимальное вращение плоскости поляризации и появление резонанса угла Фарадея достигается при максимальной конверсии волны с ТМ-поляризацией в волну с ТЕ-поляризацией, которая происходит при возбуждении ТЕ-моды в намагниченном слое. В свою очередь формирование резонансов угла Фарадея при толщинах намагниченного слоя, соответствующих ТМ-модам, происходит из-за конверсии волны с ТЕ поляризацией в волну с ТМ-поляризацией.

Отметим, что при толщинах, соответствующих возбуждению в пленке TM-мод, наблюдаются минимумы пропускания. Качественное объяснение этих минимумов состоит в том, что золотая решетка работает как поляризатор, пропускающий волны с ТМ-поляризацией из слоя наружу и отражающий волны с ТЕ-поляризацией. На рис. 5 представлены расчетные графики коэффициента отражения и угла Керра от толщины пластинки ( X = 883,7 нм ) .

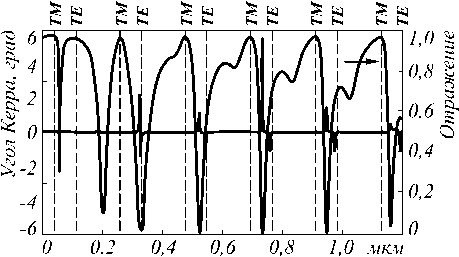
Рис. 5. Отражение и угол Керра в зависимости от толщины намагниченного слоя при нормальном падении волны. Вертикальные линии обозначают толщины возбуждения мод

Угол Керра соответствует углу между большой осью эллипса поляризации для волны в нулевом отраженном порядке дифракции и осью OX . График пропускания на рис. 5 имеет минимумы отражения при толщинах возбуждения ТЕ-мод и максимумы – при толщинах возбуждения ТМ-мод, что подтверждает сделанное предположение. График угла Керра имеет пики при толщинах возбуждения ТЕ-мод. Пики угла Керра объясняются следующим образом. Вследствие неидеальности волноводного распространения имеет место частичная диффузия волны с ТЕ поляризацией из слоя в область над решеткой. В результате отраженная от решетки волна приобретает ТЕ-компоненту, что и приводит к формированию пиков угла Керра.

Исследование трёхслойной структуры

В работе [20] показано, что трехслойная система, содержащая две субволновые серебряные решетки, разделенные диэлектрическим слоем, позволяет уве- личить коэффициент пропускания по сравнению с одной дифракционной решеткой, обладающей эффектом экстраординарного пропускания.

В связи с этим были также исследованы магнитооптические свойства трехслойной структуры, содержащей две одинаковые золотые дифракционные решетки, разделенные намагниченным диэлектрическим слоем из Bi:YIG (рис. 6).

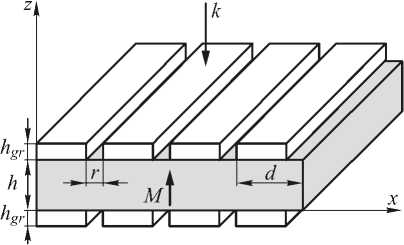
Рис. 6. Геометрия исследуемой трехслойной структуры

Расчет параметров трехслойной структуры производился с использованием оптимизационной процедуры. В качестве целевой функции было выбрано отношение произведения коэффициента пропускания и угла Фарадея для нулевого прошедшего порядка к аналогичному произведению для магнитного слоя в оптически согласованной среде:

T 0 |фо|/ T 0 |Фо| ^ max

где T 0 и ф ₀ - коэффициент пропускания и угол Фарадея для трехслойной структуры, T 0 и ф ₀- коэффициент пропускания и угол Фарадея для магнитного слоя в оптически согласованной среде. Оптимизация проводилась по 4-м параметрам: толщина дифракционной решётки, толщина магнитного слоя, период решётки, размер отверстия. Как и для двухслойной структуры, рассматривалось нормальное падение TM-поляризованной волны. В результате оптимизации была получена следующая структура: период d = 832,19 нм, ширина отверстий r = 362 нм, толщина решеток h gr = 194,23 нм, толщина магнитного слоя h = 832,11 нм.

На рис. 7 и рис. 8 представлены зависимости пропускания и угла Фарадея от толщины намагниченного слоя и длины волны.

Для толщины намагниченного слоя 832,1 нм при длине волны 883,7 нм имеем увеличение угла Фарадея по сравнению с магнитным слоем в оптически согласованной среде в 17 раз при пропускании 46%. Отметим, что добавление дополнительных параметров оптимизации, таких, как различная толщина и размер отверстий в решётках, приводит к дальнейшему увеличению значения угла Фарадея на 6-7% при увеличении пропускания на 3-5%. Переход от двухслойной структуры к трёхслойной позволил увеличить наилучшее значение целевой функции (8) более чем в 2 раза.

0,75   0,80    0,85    0,90   0,95 jukai

Рис. 7. Пропускание и угол Фарадея в зависимости от толщины намагниченного слоя при нормальном падении волн

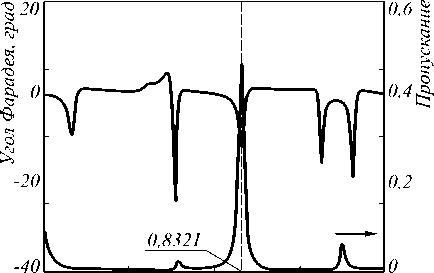
0,6     0,7      0,8         0,9 мкм

Рис. 8 Пропускание и угол Фарадея в зависимости от длинны волны при нормальном падении

Заключение

Исследованы магнитооптические свойства двухслойной структуры, состоящей из золотой бинарной дифракционной решетки и намагниченного слоя. Показано, что система обладает как резонансами пропускания, так и резонансами углов Фарадея и Керра. Представлено качественное объяснение углов Фарадея и Керра и показана их связь с волноводным распространением излучения в магнитном слое.

Рассмотрена трехслойная структура, состоящая из золотых дифракционных решеток, разделенных намагниченным слоем. Показано , что переход к трехслойной структуре позволяет получить дальнейшее увеличение значений резонансов угла Фарадея до 17 раз .

Наличие двух типов резонансов (пропускания и углов Фарадея и Керра) делает перспективным использование рассмотренных систем в оптических датчиках, использующих изменение значений резонансов при изменении физических или геометрических параметров структуры.

Работа выполнена при поддержке грантов РФФИ №07-07-97601-р_офи, 07-01-96602-р_поволжье_а, 07-07-91580-АСП_а, а также при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06).