Резонаторный метод измерения физических свойств жидкостей с применением полосковых линий

• 1.    Введение

  Важными параметрами, подлежащими высокоточному определению во многих отраслях промышленности, являются различные физические свойства жидкостей (плотность, влагосодержание и др.). В частности, требуется высокоточное определение концентрации влагосодержащих смесей (растворов). К их числу можно отнести, в частности, коптильные жидкости, в которых переменной является степень содержания одного из компонент, например, карбонильных соединений, при фиксированных значениях других компонент (фенолов, кислот и др.). С учетом существенного различия электрофизических характеристик веществ, образующих технологическую смесь, целесообразно осуществлять синтез концентратомеров на базе радиоволновых методов, обладающих известными преимуществами по сравнению с другими электрическими методами ( Викторов и др. , 1978; 1989). Наряду с синтезом датчиков на основе отрезков длинной линии ( Ершов и др. , 2007; Совлуков, Фатеев , 2007) представляет интерес их реализация с применением полосковых линий ( Ершов и др. , 2008a; 2008b).

Рис. 1. Несимметричная полосковая линия с одним из проводников в виде зигзагообразной полоски

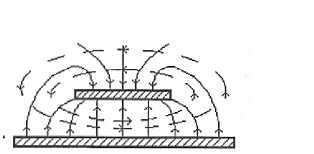
Рассматриваемую здесь полосковую линию с зигзагообразной металлической полоской можно рассматривать как длинную линию; взаимным влиянием электромагнитных полей участков этой линии можно пренебречь при расчете характеристик распространения электромагнитных волн вдоль такого отрезка линии. Волна квази-ТЕМ в рассматриваемой полосковой линии переносит часть электромагнитной энергии в подложке, а часть - в окружающем пространстве, в данном случае в жидкости, концентрация которой подлежит определению.

а)

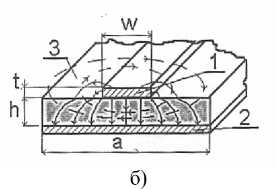
Рис. 2. Несимметричная полосковая линия: а) с воздушным заполнением между проводниками; б) с диэлектрической подложкой между проводниками

Эффективную диэлектрическую проницаемость Е эфф _o для волны квази- ТЕМ в НПЛ с диэлектриком 3 между проводниками 1 и 2, имеющим диэлектрическую проницаемость е , и окружающим линию воздушным пространством можно выразить следующей формулой, если считать толщину t полоски 1 пренебрежимо малой ( Пименов и др ., 2000):

£ + 1        £ + 1

• £ . . =--1--

  
  

эфф о      2                       1 .

2(1 +10 h / w )²

Волновое сопротивление W_л данной НПЛ можно выразить следующей формулой с относительной погрешностью, не превышающей 0,6 % ( Пименов и др. , 2000):

W £   =____________ ¹²⁰ ^ ____________ при w / h > 2,

"^ ^{эфф 0}    w / h + (2/ п )ln[17,08( w /2 h + 0,92)]

W_л 4£ эфф^ = 60[ln(8 h / w ) + w ²/(32 h ²)]   при w / h < 2.

При конечной толщине t полоски 1, в случае 0 < t1h < 0,1, сопротивление Z" можно определить по формулам (2) и (3), если вместо w/h подставить w7h, где w7h = wIh + t [1 + ln(2 h1t)] / (nh) при wIh > 0,16,                          (4)

w 7 h = w / h + t [1 + ln(4 n w / t )] / ( nh ) при w / h < 0,16.                         (5)

Для определения концентрации датчик в виде отрезка полосковой линии следует подсоединить к электрической схеме в качестве ее элемента и, измеряя тот или иной параметр этой схемы, судить об измеряемом параметре. При этом, в зависимости от выбранных структурной схемы измерения и информативного параметра датчика, возможны различные реализации схем устройств для измерения тех или иных физических свойств жидкостей. Информативными параметрами резонаторных датчиков могут, в частности, служить: резонансная частота электромагнитных колебаний отрезка полосковой линии, рассматриваемого в качестве резонатора; резонансная частота электромагнитных колебаний отрезка полосковой линии, рассматриваемого в качестве оконечной нагрузки отрезка длинной линии. Рассмотрим возможные методы реализации резонаторных измерительных устройств, соответствующие этим информативным параметрам.

• 1    – резонансный датчик;

• 2    – автогенератор;

• 3    – делитель частоты;

• 4    – преобразователь частота/напряжение

Рис. 3. Структурная схема одноканального измерительного устройства

• 1    – образцовый датчик;

• 2    – рабочий датчик;

• 3    – автогенератор;

• 4    – делитель частоты;

• 5    – вычитающее устройство;

• 6    – преобразователь частота/напряжение

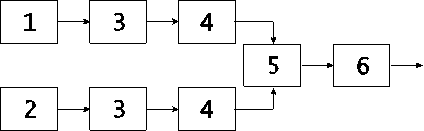
Рис. 4. Структурная схема двухканального измерительного устройства

Анализ известных структурных схем измерителей с преобразованием резонансных частот ( Викторов и др. , 1978) показывает, что наиболее приемлемыми для построения измерителей физических свойств жидкостей является автогенераторные схемы. Эти схемы выгодно отличаются от остальных простотой реализации и высокими метрологическими характеристиками. Основным фактором, ограничивающим область применения таких схем, является требование, чтобы добротность датчика была бы не менее 10. Однако это требование можно выполнить достаточно легко с помощью датчиков с диэлектрической оболочкой.

На рис. 3 представлена структурная схема одноканального измерительного устройства, состоящая из резонансного датчика 1, автогенератора 2, делителя частот 3 и преобразователя частота/напряжение 4. Датчик включается в частотозадающую цепь автогенератора и определяет его частоту генерации. Обычно генерируемые частоты лежат в диапазоне от единиц до сотен мегагерц и зависят в основном от геометрических размеров датчика. Высокочастотные колебания затем поступают на делитель частоты, в котором происходит понижение частоты генератора до требуемой величины (обычно ~ 10 кГц). После этого сигнал подается на преобразователь частота/напряжение.

Для технической реализации этой системы требуется всего 3 микросхемы и один транзистор, поэтому эта схема занимает небольшой объем и легко может быть размещена в головке датчика. Недостатком одноканальной схемы является необходимость подстройки "нуля", т.к. параметры как самой контролируемой среды, так и параметры автогенератора подвержены различного рода возмущающим воздействиям (температура, влажность, старение и т.д.).

От этого недостатка в значительной степени свободна схема двухканального измерительного устройства (рис. 4), которое от одноканального устройства отличается наличием двух датчиков: датчика образцовой жидкости 1 и датчика контролируемой жидкости 2. Датчики находятся в одинаковых условиях и поэтому все возмущающие воздействия приводят к одинаковым изменениям резонансной частоты, которые компенсируются в схеме вычитания 5. Помимо указанных выше узлов эта схема состоит из двух автогенераторов 3, двух делителей частоты 4 и преобразователя частота/напряжение 6.

Датчик представляет собой отрезок полосковой линии, разомкнутый или короткозамкнутый на одном из концов. Другим концом этот отрезок линии подключен к электронному блоку, осуществляющему возбуждение в отрезке линии электромагнитных колебаний и измерение его резонансной частоты f как функции измеряемого физического параметра К жидкости, например, концентрации бинарной смеси (раствора). Для такого отрезка линии зависимость f ( K ) имеет вид:

f ( K ) = f [ έ эфф ( έ см ), f 0 ],

где έ см = ε^' см – iε^" см – комплексная диэлектрическая проницаемость жидкости, в частности, бинарной смеси (раствора); ε^'_см и ε^"_см – действительная и мнимая составляющие έ_см ; έ_э фф ( έ_см ) – эффективная комплексная диэлектрическая проницаемость для полосковой линии, зависящая от диэлектрической проницаемости жидкости έ_см ; f ₀ – начальное значение резонансной частоты f , соответствующее отсутствию контролируемой жидкости.

Как следует из ( Никулин, Седельникова , 1992), зависимость έ эфф ( έ см ) может быть представлена так:

a (i&_CM — 1) см

C см где еэффо - эффективная диэлектрическая проницаемость для полосковой линии в отсутствие контролируемого вещества; ее величина выражается формулой (1); параметры a и b в (7) находят методом наименьших квадратов при помощи модели трехслойной полосковой структуры, описанной в (Yamashita, Mittra, 1968; Yamashita, 1968).

Для разомкнутого на конце отрезка рассматриваемой линии его резонансная частота f 0 может быть выражена следующей формулой ( Викторов и др. , 1978):

f 0 =

c n

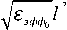
n = 1,2,...,

где n = 1,2,… – номер типа колебаний (гармоники), возбужденного в отрезке длинной линии; l – длина отрезка длинной линии; с = 3∙10⁸ м/с – скорость света.

Для отрезка полосковой линии, короткозамкнутого на одном из концов, будем иметь:

c (2 n +1)

J 0        /-------- , n    0,¹,²,--- .

⁴ ^эфф 0 ^

Для отрезка полосковой линии, короткозамкнутого на обоих концах, выражение для f ₀ имеет следующий вид:

f 0 =    rc n— , n = I,²,----                                     (10)

²V ^е эфф 0 I

Данная формула идентична (8). В обоих случаях резонатор является полуволновым; его длина пропорциональна числу полуволн вдоль отрезка длинной линии в соответствии со значением n (номером типа колебаний, или гармоники).

Для разомкнутого на конце отрезка полосковой линии его резонансная частота f , соответствующая присутствию контролируемого вещества, может быть выражена следующей формулой:

f=

c n

, n = 1,2,

где n = 1,2,… – номер типа колебаний (гармоники), возбужденного в отрезке длинной линии; l – длина отрезка длинной линии; с = 3∙10⁸ м/с – скорость света.

Для отрезка полосковой линии, короткозамкнутого на одном из концов:

f=

c (2 n + 1)

,

, ^C эфф'

n = 0,1,2,----

Для отрезка полосковой линии, короткозамкнутого на обоих концах:

f =

c n

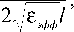
n = 1,2,----

Значение резонансной частоты f ₀ можно определить экспериментально для рассматриваемых резонаторов в виде отрезков полосковой линии, в частности, в виде короткозамкнутого или разомкнутого отрезков полосковой линии- Тогда, согласно формулам (8), (9) или (10) можно найти значение г эфф - При экспериментах с контролируемым веществом, в частности, с влагосодержащей жидкостью, измеряя значение резонансной частоты f рассматриваемого резонатора, можно, согласно (11), (12) или (13), определить с помощью функциональной зависимости f(г эфф ) значение г эфф - Затем, подставив найденные значения г эфф и г эфф ₀ в формулу (7), можно получить значение диэлектрической проницаемости жидкости г см ( K), где K - величина измеряемого параметра, в частности, концентрация контролируемой смеси (раствора)- Для расчета диэлектрической проницаемости г см бинарных смесей предложено большое число формул, вывод которых базируется на различных теоретических и экспериментальных данных ( Богородицкий , 1965; Тареев , 1982). Их практическое применение, как правило, имеет место после экспериментального подтверждения для конкретных смесей контролируемых веществ.

Следовательно, зная параметры измерительной ячейки в виде отрезка несимметричной полосковой линии – резонатора, а также начальные параметры данной ячейки, можно, измерив резонансную частоту заполненной жидкостью измерительной ячейки (полосковой линии) и используя рассмотренные выше методику измерений и полученные соотношения, найти величину того или иного измеряемого физического параметра контролируемой жидкости, в частности, концентрацию смеси веществ (раствора).

4. Заключение

Рассмотренный резонаторный метод измерения может быть применен для контроля концентрации смесей веществ (растворов), в том числе влагосодержания жидкостей, и других физических свойств веществ. Как датчики на основе отрезков полосковой линии, так измерительные устройства в целом достаточно просты в реализации.