Результаты испытаний инерциального измерительного блока в составе стенда несущей системы беспилотного вертолета

погрешностей МИНС в автономном режиме работы в условиях воздействия возмущений от двигателя беспилотного вертолета (БВ).

Методика и последовательность проведения исследования. Рассматривается работа МИНС в условиях функционирования на неподвижном основании в составе исследовательского стенда. Методически последовательность испытаний включает этапы:

• -    измерение при отсутствии возмущений, считаемое эталонным;

• -    измерение при наличии возмущений в крейсерском режиме работы двигателя;

• -    полунатурное моделирование работы БИНС, статистическая обработка результатов.

Полученные экспериментальные записи обрабатываются с помощью методов статистического анализа и отклонений Аллана [1, 2].

Инерциальный измерительный блок. В качестве аппаратной платформы применен инерциальный блок марки БДПИ-ММ, разработанный в ОАО КБПА [3]. В качестве чувствительных элементов в БДПИ-ММ применены ММГ CRG20 (ф. Silicon Sensing) и ММА ADXL203 и ADXL321 (ф. Analog Devices).

Рис. 1. Общий вид ИИБ марки БДПИ-ММ

Математическая модель полунатурного моделирования. При полунатурном моделировании реализовывался алгоритм предварительной обработки информации ИИБ и алгоритм функционирования автономной бесплатформенной инерциальной системы ориентации. Предварительная обработка информации осуществлялась с помощью цифрового фильтра Кал-мана [1, 2].

Таблица 1. Основные характеристики БДПИ-ММ

Датчик	Параметр	Характеристика
Параметр ММГ	диапазон измерения не менее, º/с	±150;
	нулевые сигналы не более, º/с	0,2;
	погрешность масштабного коэффициента, %	2;
Параметр ММА	диапазон измерения не менее, м/с2	±100;
	нулевые сигналы не более, м/с2	0,05;
	погрешность масштабного коэффициента, %	2;

Оптимальная оценка описывается рекуррентным соотношением вида:

x( n + 1) = F ( n ) • x ( n ) + K ( n ) • [ z ( n ) - H ( n ) • F ( n ) • x ( n ) ] ^, априорную матрицу дисперсии определим из выражения:

P (n +1) = F (n) • P (n) • FT (n) + G (n) • Q (n) • GT (n)

, вычислим коэффициент усиления фильтра Калмана:

K ( n + 1) = P ( n ) • H^T ( n ) • [ H ( n ) • P ( n ) H^T ( n ) + R ( n ) ]^{- 1}

, апостериорную матрицу дисперсии вычислим из выражения:

P ( n + 1) = [ E - K ( n ) • H ( n ) ] • P ( n )

где x ( n + 1) - оценка сигнала, F ( n ) - матрица состояния, G ( n ) - матрица возмущения, R ( n ) - матрица дисперсий, E -единичная матрица.

При построении математической модели фильтра Калмана за основу принята дискретная модель формирующего фильтра первого порядка для белого шума [2, 5]:

x ⁽ n + 1) = ^{(1 -} ц^ ^T ) • x ⁽ n ) +     (5)

T • 2 • D_x • ц • w ( n )

где D x - дисперсия сигнала, w ( n ) - порождающий белый шум, µ - интенсивность белого шума, T - период дискретизации.

В соответствии с (5) переходная матрица измерения H ( n ), матрицы состояния F ( n ) и возмущения G ( n ) принимают вид:

F (n) *(1 - ц^ T) G (n) « T • V 2 • Dx • ц

,                                                                          ,

H ( n ) = [ 1 ]

Численные значения D x , µ , T были получены экспериментально. T =0,004 с. Для сигналов ММГ: F ( n )=0,996; G ( n ) « 0,004 • V2 • 0.9995 Л = 0.0056град. Для сигналов ММА: F(n)≈(1 – 1 x 0,004)=0,996; G(n)=0,0030 м. При расчете из трех дисперсий сигналов по каналам x, y, z выбрано большее значение.

Начальные матрицы дисперсии P ( n ) и ковариации Q ( i ) найдем из выражений:

P ( n ) = P (0)

,

M [ ц ( i + 1) w^T ( j + 1)] = Q ( i ) ,

Для сигнала ММА Q 1 =1,5380e-04 м²/с⁴, для сигнала ММГ Q 1 = 0,2933 град²/с².

При определении углов пространственной ориентации применены кинематические уравнения в па- раметрах Родрига-Гамильтона [4, 7]:

2•тЛ = ЛоQ-Qg оЛ + Л[1 -|A|]

,

где ^Q = i ® x ⁺ j'®y ⁺ k®_z - гиперкомплексное отображение вектора абсолютной угловой скорости на оси связанного трехгранника, ^Q g = i ® xg ^{+ j} ® y,_g ^{+ k} ® _Zg - гиперкомплексное отображение вектора абсолютной угловой скорости на оси географического трехгранника.

Углы пространственной ориентации найдем из выражения [6, 7]:

( 2 ^^ - 2 ^^ 1

^ ^инс = acrtg I--v²----т-⁰-^ I

( 2X 2 + 2 2 0 - 1 J

,

^“с = arcsin(2X22 - 2202з)

,

Г 2 XX - 2 XX 1

у ^инс = arcsin I-- 2--³ z-° ¹ I 2 X 2 + 2 X 2 -¹ J

Для компенсации ухода нормы кватерниона в выражении (7) введен член Л • [1 - ||Л||], который обес- печивает автоматическую коррекцию ухода нормы кватерниона.

Исследовательский стенд несущей системы БВ. Стенд несущей системы БВ предназначен для наземной отработки системы управления двигателя, системы охлаждения, системы электроснабжения, топливной и масляной систем с использованием технологической колонки несущих винтов.

Рис. 2. Трехмерная модель стенда несущей системы БВ

Стенд состоит из следующих элементов: основание стенда (имитатор фюзеляжа), агрегат силовой (моторама и двигатель), несущая система без винтов (колонка, редуктор, муфта, подредукторная рама), топливная система, система охлаждения, система электроснабжения, система отвода отработавших газов, система вентиляции, противопожарная система двигателя, пилотажно-навигационный комплекс ПНК, система управления двигателем СУД, система нагружения (загружатель валов колонки, загружатели автоматов перекоса, блок управления системой нагружения, имитатор лопастей), измерительный комплекс, сеть кабельная. Основанием стенда служит металлический каркас, на котором крепятся все элементы и системы. Стенд БВ позволяет провести комплексное моделирование работы систем реального ЛА, в том числе и малогабаритной навигационной системы.

Результаты экспериментального исследования и полунатурного моделирования. Исследование характеристик сигналов ММГ CRG20 и ММА ADXL203 и ADXL321 осуществлялось по натурным записям датчиков БДПИ-ММ. Регистрация сигналов ММГ ® x , ® y , to z и ММА а х , а у , a z проводилась в течение 300 секунд с частотой 250 Гц. На рис. 3 и рис. 4 приведены примеры записей сигналов при оборотах двигателя 0 и 4000 об/мин, соответственно. На рис. 5 и 6 приведены графики спектров амплитуд сигналов ММА в этих же режимах. Аналогичные графики сигналов ММГ и спектров приведены на рис. 7-10. В табл. 2 сведены СКО и математические ожидания сигналов ММГ и ММА.

0.02

rnrWi

-0.02

= -0.04

J ь til Jib IL1M.L J. 1 кШ^ШЬ^ IUU Jb^O JiJMuUIlj fcmibi uiiiu u

50         75        100

Время, c

Рис. 3. График сигнала ММА а х (м/с²) при 0 об/мин.

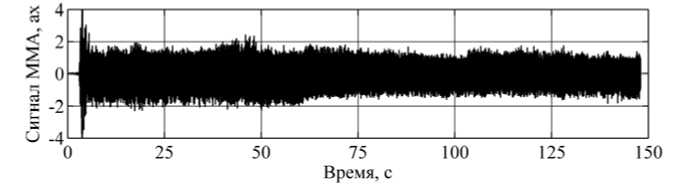
Рис. 4. График сигнала ММА а х (м/с²) при 4000 об/мин.

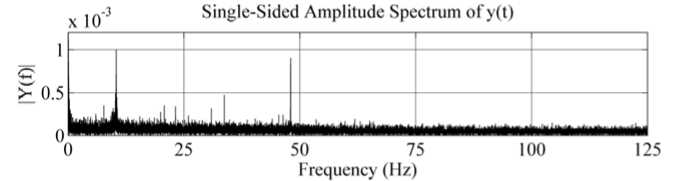
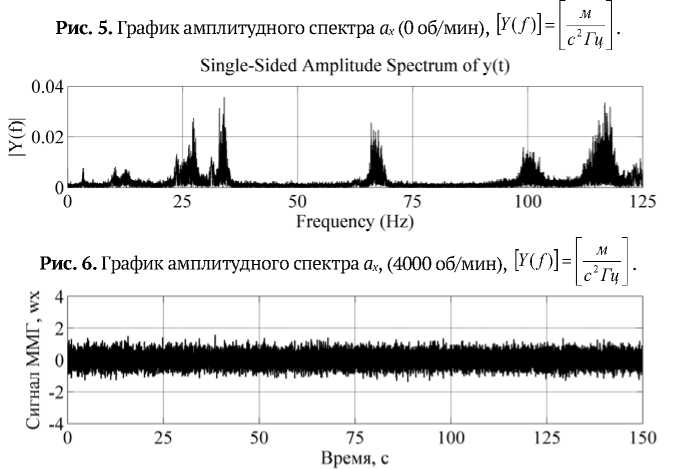
Рис. 7. График сигнала ММГ to _x (град/с) при 0 об/мин.

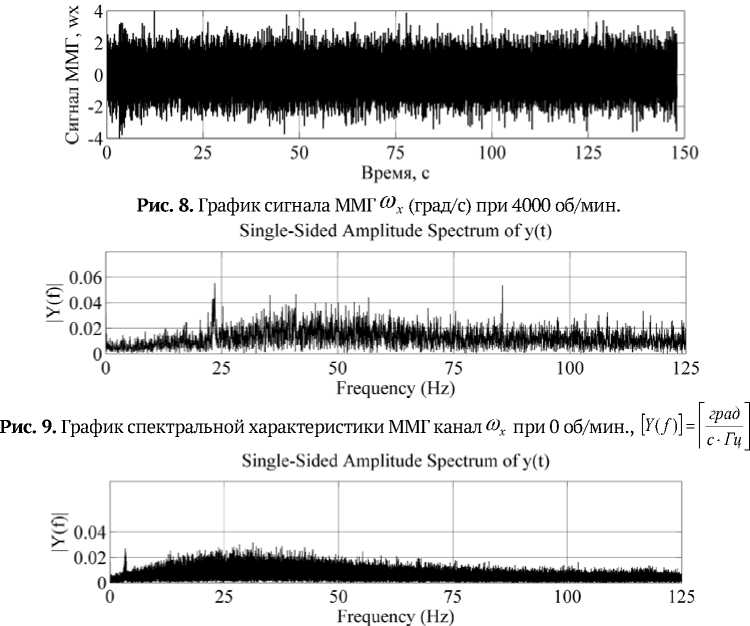
Рис. 10. График спектральной характеристики ММГ канал ra x при 4000 об/мин.,

Из табл. 2 следует, что при работе двигателя математические ожидания погрешностей ММГ увеличиваются от 0 до 6 раз. СКО погрешностей ММГ увеличиваются примерно в 3 раза. Предварительная обработка информации дает несмещенные оценки угловых скоростей со снижением СКО на 2 порядка при неработающем приводе и на порядок – при включенном двигателе. Математические ожидания погрешностей ММА при работе привода меняются несущественно. СКО погрешностей ММА увеличиваются от 30 до 80 раз. Предварительная обработка информации дает несмещенные оценки кажущихся ускорений со снижением град с • Гц

СКО на 2 порядка при неработающем приводе и на порядок – при включенном двигателе. Графики спектральной плотности амплитуд сигналов ММА свидетельствуют о появлении множества резонансов на частотах от 10 до 120 Гц, обусловленных элементами конструкции стенда. ПОИ позволяет снизить амплитуды этих составляющих примерно на 2 порядка.

Для исследования состава погрешностей во временной области построены графики вариаций Аллана сигналов a x и ® х (рис. 11,12).

Таблица 2. Статистические характеристики погрешностей датчиков ИИБ

Параметр	Обороты двигателя об/мин.	Данные ИИБ (без фильтрации)		После предварительной обработки (ПОИ)
		матем. ожидание	СКО	матем. ожидание	СКО
Продольная составляющая угловой скорости ® х , град/с	0	0.0393	0.3736	0.0394	0.0034
	4000	0.0164	0.9997	0.0165	0.0094
Поперечная составляющая угловой скорости ® z , град/с	0	-0.0295	0.3146	-0.0293	0.0030
	4000	-0.1838	0.7586	-0.1860	0.0598
Нормальная составляющая угловой скорости ® y , град/с	0	-0.0232	0.1892	-0.0231	0.0011
	4000	-0.1004	0.6355	-0.1028	0.0612
Продольная составляющая кажущегося ускорения а х , м/с2	0	-0.0196	0.0065	-0.0196	4.3908e-04
	4000	-0.00723	0.5350	-0.0072	0.0024
Нормальная составляющая кажущегося ускорения, а у, м/с2	0	-0,0076	0.0157	-0,0098	0.0088
	4000	-0.0724	0.3608	-0.0806	0.0063
Поперечная составляющая кажущегося ускорения а z , м/с2	0	-0.0976	0.0085	-0.0976	2.3563e-04
	4000	-0.0347	0.4988	-0.0348	0.0023

Время, секунды

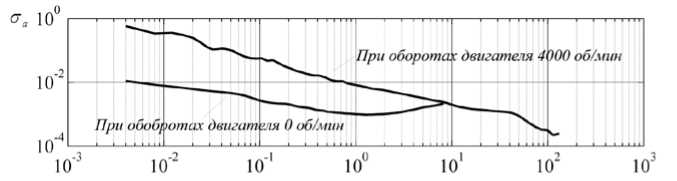
Рис. 11. График отклонений Аллана ^CT a сигнала a _x , данные ИИБ, [ ст _я ] =(м/с²).

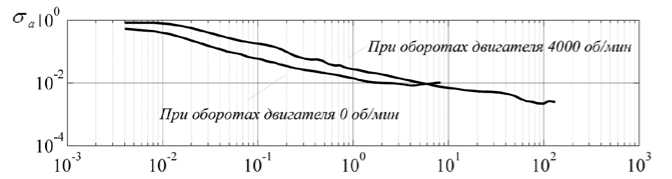
Рис. 12. График отклонений Аллана ro x , данные ИИБ, [ с _а ] =(град/с).

Из графиков отклонений Аллана следует, что в сигналах ММА и ММГ присутствует белый шум, уровень которого увеличивается при работающем приводе на порядок у ММА и в 15 раз у ММГ. Сравнить остальные характеристики не представляется возможным из-за малой длительности записей сигналов. При полунатурном моделировании БИНС на основе БДПИ-ММ оценивались погрешности (табл. 3) вычисления углов ориентации (курса, крена и тангажа) (рис. 13). Из табл. 3 и рис. 13 видно, что при влиянии возмущений от двигателя погрешности вычисления углов ориентации увеличиваются в 1,1-8,6 раза.

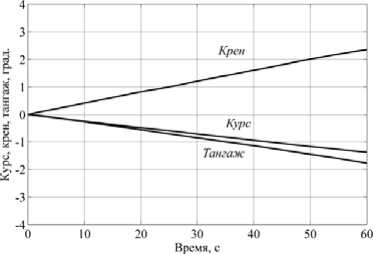
а)

Рис. 13. Графики изменения вычисленных углов ориентации: а)при 0 об/мин, б) при 4000 об/мин.

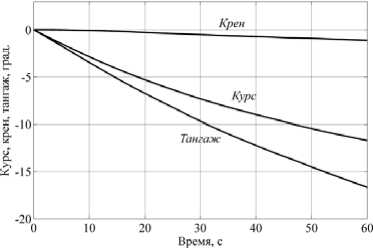
б)

Таблица 3. Оценки погрешностей

Наименование параметра	Обороты двигателя об/мин.	Ошибка определения ориентации (СКО)
		За время 60 с.(1 мин.)
инс курс ψ  , град.	0	0.3875
	4000	3.3352
инс крен γ , град.	0	0.6301
	4000	0.7038
инс тангаж, ϑ , град.	0	0.5487
	4000	4.8066

Выводы: Проведено экспериментальное исследование влияния вибрационных возмущений от двигателя стенда несущей системы беспилотного вертолета на измерения инерциального измерительного блока на основе микромеханических гироскопов и акселерометров. При работе двигателя математические ожидания ошибок измерения угловых скоростей увеличиваются в 6 раз. Математические ожидания ошибок измерения линейного ускорения изменяются незначительно. СКО погрешностей ММГ увеличиваются примерно в 3 раза, у ММА - от 30 до 80 раз. Предварительная обработка информации дает несмещенные оценки угловых скоростей и кажущихся ускорений со снижением СКО на 2 порядка при неработающем приводе и на порядок – при включенном двигателе.

Проведен анализ характеристик погрешностей методами спектрального анализа и вариаций Аллана. Из графиков отклонений Аллана следует, что в сигналах ММА и ММГ присутствует белый шум, уровень которого увеличивается при работающем приводе на порядок у ММА и в 15 раз у ММГ. Сравнить остальные характеристики не представляется возможным из-за малой длительности записей сигналов. В результате полунатурного моделирования бесплатформенной инерциальной системы ориентации получено, что погрешности (при оборотах 0 об/мин) вычисления курса, крена и тангажа за 60 секунд достигают 0.2727, 0.5102 и 0.6902 градуса соответственно. При наличии возмущений от двигателя ошибки увеличиваются до значений 1.3279, 1.8129 и 1.0329 градуса соответственно. Повышение точности ИИБ и МИНС в целом связано с применением математической модели погрешностей ММГ и ММА при калибровке и предварительной обработке информации ИИБ, увеличением порядка ФК и учетом разных значений дисперсий сигналов датчиков, введением коррекции в кинематические уравнения и уравнения определения координат.