Результаты исследования динамики горизонтального решета для сепарации кедрового ореха

Разработанная на кафедре автомобилей, тракторов и лесных машин СибГТУ экспериментальная установка для переработки кедровых шишек решает проблему выделения семенного ореха в местах заготовки [1].

Все лабораторные опыты выполнялись с кедровыми шишками, заготовленными в сентябре 2011 г. в Ермаковском и Манском лесничествах. Влажность кедровых шишек составила 15 %.

Целью данной работы является изучение движения кедрового вороха на горизонтальном решете при изменении амплитуды и частоты колебаний решетного стана для отделения ореха и самоудаления шелухи.

Технологический процесс переработки шишек подразделяется на дробление шишек, получение кедрового вороха и отделение ореха от шелухи. Наиболее сложной задачей является разделение кедрового вороха, так как ворох состоит из кедрового ореха, чешуек и остовов шишек.

Анализ процесса выделения кедрового ореха позволяет сделать вывод о том, что наиболее перспективным в этом плане являются приемные устройства с возможностью колебаний [2]. Для обоснования параметров динамики горизонтального решета по разделению вороха были проведены опыты с применением теории планирования эксперимента [3].

На эффективность просеивания кедрового вороха влияют такие факторы, как амплитуда колебаний ( А, м ), частота вращения приводного вала ( f, Гц ) и подача вороха на горизонтальное решето ( m, кг ).

В качестве метода обработки экспериментальных данных был принят план 33, в котором исследуемые параметры изменяются на трех уровнях: верхнем, основном и нижнем, и который имеет 27 точек при трехкратной его повторности.

Уровни и интервалы варьирования факторов представлены в таблице 1, план эксперимента в таблице 2.

Кодовое обозначение факторов

Таблица 1

Наименование фактора	Обозначение		Интервал варьирования фактора	Уровни варьирования фактора
	натуральное	нормализованное		нижний (–1)	основной (0)	верхний (+1)
Амплитуда колебания, м	А	х 1	0,01	0,02	0,03	0,04
Частота колебания, Гц	ƒ	х 2	0,25	2,67	2,92	3,17
Масса вороха, кг	m	х 3	0,5	0,5	1,0	1,5

Таблица 2

№	х 1	х 2	х 3
1	–1	–1	0
2	0	0	–1
3	1	1	1
79	0	–1	–1
80	0	0	0
81	1	0	1

План эксперимента 33 (начало и окончание таблицы)

С целью оптимизации процесса и установления степени влияния варьируемых технологических факторов на выход шелухи и чистого ореха, на основании таблиц 1,2, средствами пакета Statgraphics были получены математические модели параметров процесса просеивания, которые после оценки значимости коэффициентов регрессии имеют вид:

• 1)    для математического описания прогнозирования схода шелухи при просеивании на горизонтальном решете

  у 1 = 0 , 38916 - 0 , 00503704 х 1 + 0 , 00455556 х 2 + 0 , 0949074 х ₃ - 0 , 0114074 х 12 - 0 , 101685 х ₃ 2 ; (1)

• 2)    для математического описания прогнозирования выхода ореха при просеивании на горизонтальном решете

  у ₂ = 0 , 524049 + 0 , 0162407 • х 1 + 0 , 0472963 • х ₂ + 0 , 265815 • х ₃ - 0 , 0339074 • х 1 ² - 0 , 0154074 х ₃ ² . (2)

Проанализировав регрессионные уравнения, можно сделать вывод о том, что наибольшее влияние на выход кедрового ореха при просеивании на горизонтальном решете имеет такой фактор, как х 3 – масса вороха, в меньшей степени – частота (х 2 ) и амплитуда колебаний (х 1 ).

Оптимизация параметров процесса просеивания на горизонтальном решете проводилась по результатам статической обработки данных эксперимента. Для этого в качестве откликов были приняты: отделение шелухи (у 1 ) и выход ореха (у 2 ) при просеивании. Из перечисленных выше факторов для достижения поставленной цели основным является максимальный выход ореха (у 2 ).

Определено, что оптимальные условия просеивания кедрового вороха и отделение ореха от шелухи будут осуществляться на горизонтальном решете при амплитуде колебаний х 1 = 0,032 м, частоте х 2 = 3,17 Гц и подаче вороха х 3 =1,5 кг.

Подставив в уравнение регрессии значения х 1 , х 2 и х 3 для максимального выхода ореха, выполним проверочный расчёт по у 2

у ₂ = 0 , 524049 + 0 , 0162407 • х 1 + 0 , 0472963 • х ₂ + 0 , 265815 • х ₃ - 0 , 0339074 • х 2 -

• -    0 , 0154074 • х ₃ ² = 0 , 524049 + 0 , 0162407 • 0 , 217344 + 0 , 0472963 • 1 , 0 + 0 , 265815 • 1 , 0 -           (3)

• -    0 , 0339074 • 0 , 217344 2 - 0 , 0154074 • 1 , 0² = 0 , 82368098689 - 0 , 823681 .

Доверительные интервалы для параметра у 2 – выходу ореха.

Для этого воспользовались обработкой статистических данных. При выборочном среднем арифметическом значении µ = 0,305, минимальном и максимальном значении массы ореха – min m ор = 0,024 кг, max m ор = 0,038 кг, преобразовав и подставив новые истинные значения в уравнение регрессии, получим:

у ₂ (min) = 0,524049 + 0,0162407 • х + 0,0472963 • х 2 + 0,0,265815 • х 3 - 0,0339074 • х 2 -

• -    0,0154074 • х 2 = 0,524049 + 0,0162407 • 0,217344 + 0,0472963 • 1,0 + 0,265815 • 0.7867 -     (4)

• -    0,0339074 • 0,217344 2 - 0,0154074 • 0.7867 ² « 0.773653.

у ₂ (max) = 0,524049 + 0,0162407 • х 1 + 0,0472963 • х ₂ + 0,0,265815 • х ₃ - 0,0339074 • х 1 ² -

• -    0,0154074 • х 2 = 0,524049 + 0,0162407 • 0,217344 + 0,0472963 • 1,0 + 0,265815 • 1.2459 -     (5)

• -    0,0339074 • 0,217344 2 - 0,0154074 • 1.2459 2 « 0.88056.

В натурных испытаниях действительный выход ореха составил 0,806 кг при погрешности 2,18 %.

Таким образом, теоретические значения выхода ореха и экспериментальные подтверждают адекватность полученной математической модели процесса просеивания, также об этом говорят значения коэффициента Lack-of-Fit (Statgraphics).

Также был определен доверительный интервал по параметру у 2 : при р=0,95 он находится в следующих пределах: 0,774 <  0,824 <  0,881 .

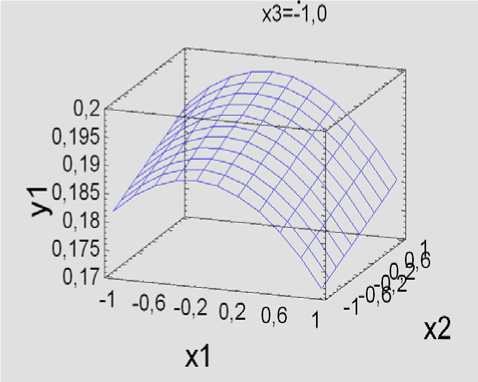
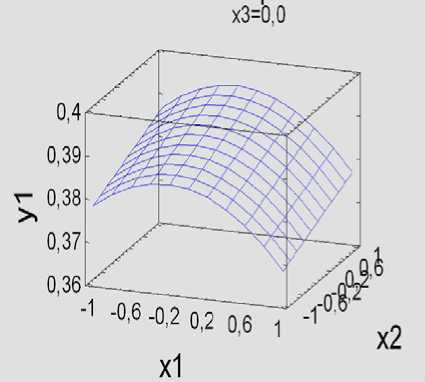
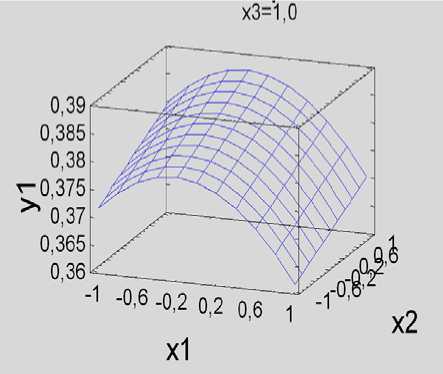
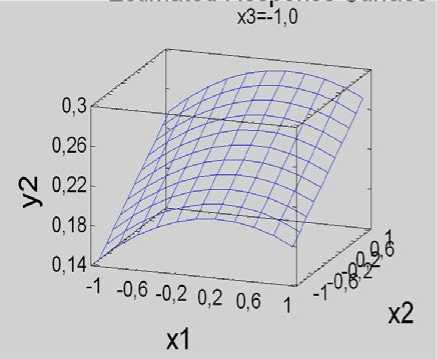
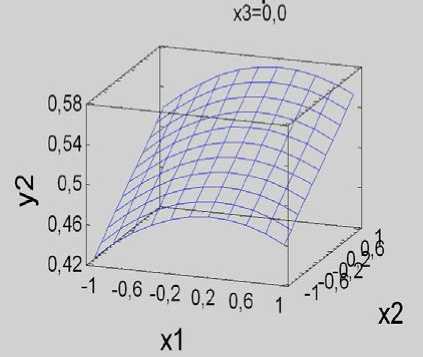
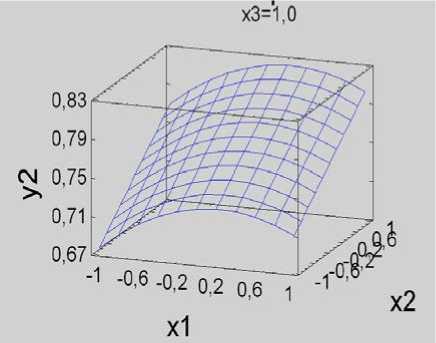
В результате проведенных исследований установлено, что выходные величины существенно зависят от всех управляемых факторов. Для наглядности результаты представлены на рисунках 1, 2.

б

в

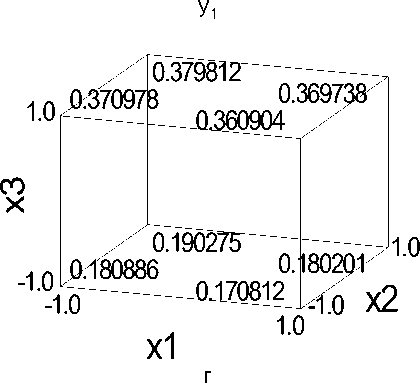
Рис. 1. Поверхности откликов по выходу массы шелухи: а – при х 3 = – 1,0; б – при х 3 = 0,0; в – при х 3 = 1,0; г – график на «Кубе»

б

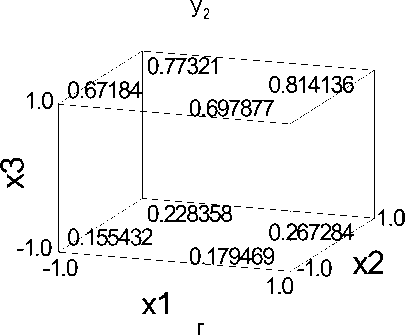
в

Рис. 2. Поверхности откликов по выходу массы ореха: а – при х 3 = – 1,0; б – при х 3 = 0,0; в – при х 3 = 1,0; г – график на «Кубе»

Таким образом, опытным путем обоснованы конструктивные и кинематические параметры работы горизонтального решета, найдена математическая модель разделения кедрового вороха в процессе просеивания.

Выводы

• 1.    В результате исследований получены зависимости, описывающие процесс динамики горизонтального решета по разделению вороха и самоудаления отходов дробления при следующих параметрах: амплитуда колебаний А = 0,032 м и частота колебаний ƒ = 3,17 Гц.

• 2.    Получены аналитические выражения, описывающие процесс движения вороха на горизонтальном решете, его разделение на кедровый орех и шелуху с самоудалением отходов дробления. Установлено, что процесс разделения вороха зависит от амплитуды и частоты колебаний, что обеспечивается кулачковым механизмом.

• 3.    В процессе натуральных испытаний экспериментальной установки подтверждена обоснованность принятых конструктивных решений. Составлены алгоритмы оптимизации полученных уравнений регрессий, процесса просеивания кедрового ореха на горизонтальном решете, позволяющие определять рациональные режимы его движения. С применением математического планирования эксперимента определены оптимальные кинематические параметры горизонтального решета.