Результаты исследования комплексного метода оценки качества оконтуривания на основе двухмерного точечного потока восстановления
Автор: Денисов В.П., Дубинин Д.В., Кочегуров А.И., Лаевский V. Geringer В.Е.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 2 т.16, 2015 года.
Бесплатный доступ
Представлены результаты исследования качества оконтуривания для трех алгоритмов (Marr-Hildreth, ISEF и Canny), полученные с помощью комплексного метода, предложенного в работе Boaventura и Gonzaga. Исследования проводились в среде программно-алгоритмического комплекса стохастического моделирования «КИМ СП». Дано краткое описание возможностей программно-алгоритмического комплекса, приведена его обобщённая структурная схема, а также показано формирование последовательности структур морфологий эталонных пространственно-временных сигналов (ЭПВС) и их растровых изображений. В ходе получения и обобщения результатов численных экспериментов были использованы методы и подходы статистического моделирования, а эталонные изображения были аппроксимированы двумерным точечным потоком восстановления. Оценки эффективности оконтуривания для трех исследуемых алгоритмов (Marr-Hildreth, ISEF и Canny) получены при различных уровнях аддитивного шума. Шум формировался датчиком случайных чисел с распределением, близким к нормальному распределению. В качестве критерия отношения сигнал/шум принималось отношение энергии сигнала к дисперсии шума. Анализ эффективности алгоритмов проводился на основе морфологий эталонных изображений ЭПВС типа A и F. Результаты исследований представлены в виде совокупности оценок обобщённого показателя качества, оценок вероятностей правильного обнаружения и пропуска контуров, а также вероятности ложной тревоги в зависимости от отношения сигнал/шум. Вычисление вероятностных оценок отдельных составляющих обобщенного критерия качества связано, прежде всего, с разной значимостью этих составляющих в таких прикладных областях, как космонавтика, навигация, геология, дефектоскопия и др. Сопоставление полученных результатов для трех алгоритмов оконтуривания и двух типов морфологий позволило не только дать объективную оценку эффективности применения комплексного метода для сравнения качества алгоритмов поиска и локализации границ, но и сформировать рекомендации по выбору в конкретной прикладной задаче того или иного алгоритма, в зависимости от уровня шума и типа морфологии, лежащей в основе построения изображения.
Двумерный точечный поток восстановления, стохастическое компьютерное моделирование, исследование на моделях, выделение контуров, оценка эффективности, сравнение алгоритмов
Короткий адрес: https://sciup.org/148177419
IDR: 148177419 | УДК: 004.932:94,
Текст научной статьи Результаты исследования комплексного метода оценки качества оконтуривания на основе двухмерного точечного потока восстановления
Введение. С развитием цифровой вычислительной техники появилась возможность создания высокоэффективных систем, предназначенных для анализа, синтеза, обработки и передачи оптической информации. Изображения являются одновременно результатом и объектом исследований в космонавтике, геологии, картографии, навигации, дефектоскопии и во многих других областях человеческой деятельности. В большинстве работ, связанных с созданием и проверкой новых алгоритмов обработки пространственновременных сигналов, имеет место ряд субъективных моментов. Одним из основных недостатков является использование в качестве эталонных изображений реальных снимков различных предметов, построек или людей [1–3]. Это позволяет провести настройку создаваемого алгоритма обработки информации на определённую предметную область, но упускаются моменты, характерные для других областей, что затрудняет оценку качества элементов программного обеспечения, проведение объективного сравнения используемых реализаций алгоритмов друг с другом. Объективным подходом к решению задачи сопоставления реализаций алгоритмов является цифровое имитирование моделирования реализуемой системы или её части. Компьютерное имитирование моделирования позволяет проведение анализа реализации исследуемого алгоритма в определённых, строго контролируемых условиях, создание предпосылок для проведения факторного анализа, формирует подходы и методы оценки качества систем и программ. Ключевым моментом в процессе компьютерного моделирования является создание многомерных стохастических полей (яркостные поля плоских изображений, температурные и другие поля атмосферы, океана и т. п. [4; 5]), которые составляют основу имитационного моделирования, позволяют вносить вероятностный фактор [4; 5] в процесс моделирования, детализировать и обобщать предмет исследования, улучшая качество постановки эксперимента [6] и качество получаемых результатов [5; 7; 8].
computer simulation, research on models, edge detection,
В настоящее время разработано большое количество алгоритмов оконтуривания, скелетизации, сегментации, привязки и т. д., что требует объективного сравнения качества реализаций алгоритмов между собой. Существует множество подходов и методов их оценки, в том числе операторов получения растрового контурного поля (РКП) [6; 9–13]. Интерес к таким работам не ослабевает [14]. В связи с этим в данной работе проведены исследования комплексного, статистического показателя качества эффективности работы операторов поиска и локализации границ, включающего четыре метрики [15; 16] в среде комплекса стохастического моделирования «КИМ СП» [17]. В ходе получения и обобщения результатов численных экспериментов использованы методы и подходы статистического моделирования, эталонные изображения аппроксимированы двумерным точечным потоком восстановления [4; 7; 8; 18]. Приведены графики составляющих статистических оценок обобщённого показателя качества при различных уровнях шума для трех квазиоптимальных алгоритмов оконтуривания (Marr-Hildreth, ISEF и Canny). Получены оценки вероятностей правильного обнаружения, ошибок первого и второго рода. Предложены направления дальнейших исследований.
Структура программного комплекса и основные этапы моделирования. В ряде предшествующих работ были сформулированы, математически формализованы и решены задачи построения структур морфологий эталонных пространственно-временных сигналов и их растровых представлений [5; 7; 8]. Проведён анализ статистики морфологии генерируемых полей [19]. Реализованы и проверены алгоритмы генерации ЭПВС [18]. Это позволило подготовить основу для этапа создания комплекса имитационного моделирования случайных пространственно-временных полей «КИМ СП». Основной целью разработки являлось создание специального математического и программного обеспечения, позволяющего генерировать эталонные пространственно-временные сигналы, проводить их статистический анализ, определять значения совокупности параметров построения поля, накапливать статистику для дальнейших экспериментов.
Программный комплекс имеет модульную структуру. Его обобщённая схема приведена на рис. 1.
Программный комплекс состоит из пяти модулей и СУБД. Модуль ввода параметров генерации эталонного пространственно-временного сигнала ( P ) позволяет пользователю задать тип морфологии формируемого стохастического поля, значение вероятностей появления формирующих элементов структуры эталонных изображений, количество и размеры ЭПВС, их маштабирование. Входные параметры могут как задаваться вручную, так и быть считаны из базы данных.
По заданной совокупности параметров модуль генерации структуры пространственно-временного сигнала формирует совокупность многомерных стохастических полей, преобразует их описание к векторному виду ( V), создает набор сегментов изображения и растровые представления ( R ).
Модуль статистической обработки позволяет оценивать характеристики и статистические свойства порожденного пространственно-временного сигнала ( X) :
-
- корреляционную функцию поля при горизонтальном, вертикальном или диагональном сдвигах;
-
- оценку зависимости среднего числа сегментов и СКО от количества отсчётов и радиуса корреляции ПВС;
-
- аналитические зависимости вышеперечисленных оценок на основе метода наименьших квадратов;
-
- статистику проверки гипотез (например, гипотезы о нормальном законе распределения среднего числа сегментов на основе критерия согласия Пирсона с учётом коррекции Йетса [20]).
Результаты статистической обработки ( X) отображает модуль визуализации. Их можно сравнить с расчетными характеристиками ( X), полученными от модуля расчета теоретических характеристик ЭПВС, и оценить степень их соответствия.
Комплекс имитационного моделирования позволяет формировать структуры различных разновидностей морфологий ЭПВС [5; 6]: A , B , C , D , E , F , FB , FC , FD , FE . Частная реализация структур случайных полей морфологии A , F , FB , FC , FD , FE приведена на рис. 2, их растровые представления - на рис. 3.
На первом этапе моделирования на основе двумерного точечного потока восстановления было создано векторное описание структур эталонных изображений с морфологиями А и F (рис. 2). Полученное векторное описание границ представляет собой не что иное, как связную последовательность координат точек, описывающих прохождение контурных векторов. Непрерывность структуры пространственно-временных сигналов обусловлена свойствами формирующего точечного потока восстановления.
На втором этапе формировалось растровое изображение размером M х K точек (рис. 3), накапливались статистики эталонных пространственно-временных сигналов обоих морфологий, их векторного и семантического описания, а также разновидностей эталонных изображений с различной степенью зашумлённости.
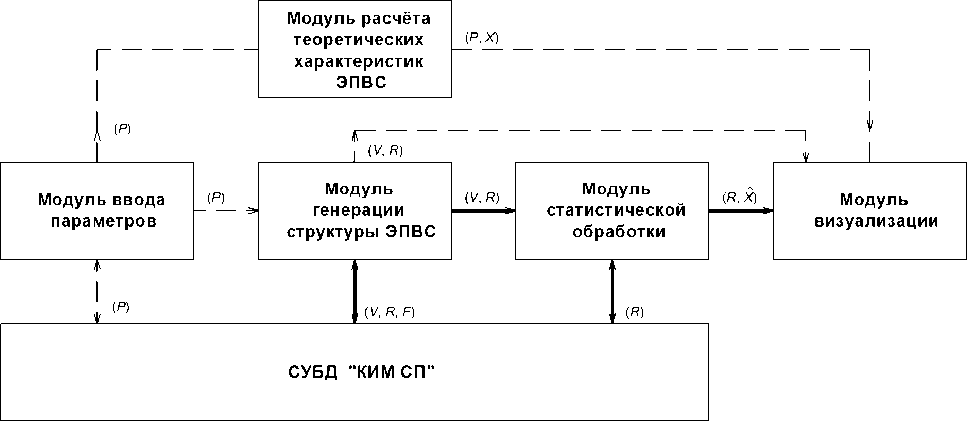
---Синхронизированный поток данных р Ошибки
------ Синхронизированный поток данных и р Параметры или их совокупность последовательность управления вычислениями
R Растровое представление ЭПВС
-
V Векторное описание структуры поля
X Характеристики ЭПВС
Рис. 1. Структурная схема комплекса имитационного моделирования
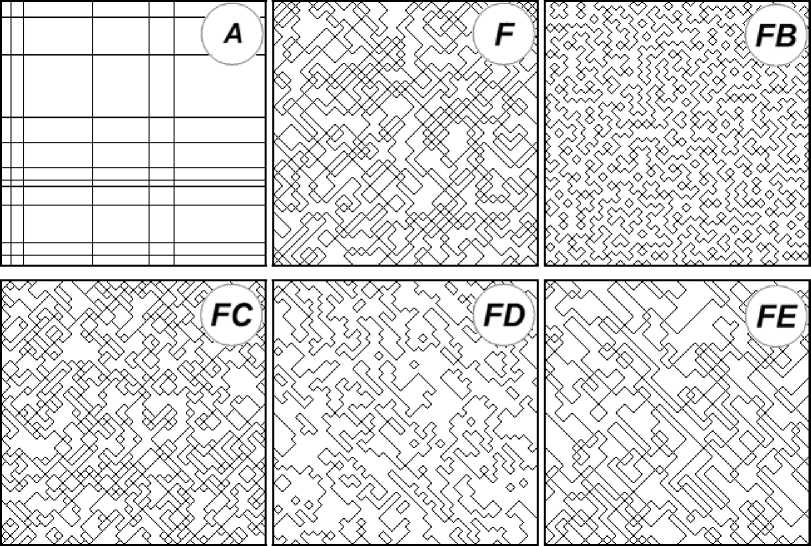
Рис. 2. Структуры морфологий A , F , FB , FC , FD , FE

Рис. 3. Растровые представления морфологий A , F , FB , FC , FD , FE
На третьем этапе результирующая серия изображений подвергалась обработке различными типами контурных детекторов с целью получения бинарного, растрового изображения контуров и необходимых данных по запланированному ходу эксперимента.
Обобщая вышесказанное, отметим, что в этой работе были использованы три разновидности операторов получения РКП изображения: Marr-Hildreth [21], ISEF
-
[22] и Canny [23]. На основе априорно известной совокупности контурных векторов производилось вычисление показателей качества детектирования, накопление необходимой статистики поведения операторов получения РКП изображения в определённых условиях. Это позволило в ходе проведения четвёртого этапа рассчитать комплексный показатель качества, предложенный Boaventura и Gonzaga, при раз-
- личных отношениях сигнал/шум для различных морфологий ЭПВС; получить оценки вероятности правильного обнаружения ошибок первого и второго рода, качества восстановленной границы на основе метрики Пратта [9] для обобщённого комплексного критерия качества в окрестности 5 × 5 при различных отношениях сигнал/шум; построить графики как составляющих, так и комплексного критерия качества оконтуривания и провести обобщение полученных результатов.
Полученные результаты и предполагаемые исследования. Эффективность методов получения растрового контурного поля трудно оценить из-за отсутствия четкого определения ряда понятий проблемной области. Например, нет строгого, математически обоснованного, формализованного определения, что является границей объекта. В работе [15] получение оценок эффективности рассматривается с позиции решения проблемы бинарной классификации. Обобщённый показатель качества представляется в евклидовом пространстве как
DL = J(P co - 1 ) 2 + ( IMP — 1)2 + P d + P fa , (1)
где P co – вероятность правильного обнаружения границы; IMP – оценка качества по критерию Пратта; P nd – вероятность пропуска границы; P fa – вероятность ложного выделения границ.
Значение обобщённого показателя качества DL изменяется в интервале от 0 до 2. Его минимальное значение получается при P co = 1, IMP = 1, P nd = 0, P fa = 0.
Сравнивая значения оценки DL для эталонных изображений, построенных на основе морфологий пространственно-временных сигналов типа А или F (рис. 4), можно заметить, что поведение DL для различных реализаций алгоритмов оконтуривания имеет общие тенденции. Например, среди операторов оконтуривания Canny, ISEF и Marr-Hildreth для всех типов изображений, оператор Marr-Hildreth является наилучшим возможным решением при получении РКП изображения для малых отношений сигнал/шум. Анализируя поведение оценки критерия качества DL для изображений, полученных только на основе морфоло- гии типа A, видно, что при отношениях сигнал/шум больших 34 дБ предпочтение необходимо отдать оператору ISEF. Оператор Canny уступает на всём промежутке значений отношения сигнал/шум оператору Marr-Hildreth, и только при отношениях сигнал/шум меньших 8 дБ незначительно превосходит оператор ISEF. Оператор ISEF лучше операторов Canny и Marr-Hildreth при больших отношениях сигнала к шуму.
Анализируя поведение оценки критерия качества DL для изображений, полученных на основе морфологии типа F , можно отметить, что оператор Marr-Hildreth позволяет значительно лучше выделять РКП изображения при отношениях сигнал/шум меньших 20 дБ. При отношениях сигнал/шум больших 20 дБ предпочтение следует отдавать оператору Canny. При этом оператор Canny показал значительно лучшие результаты детектирования диагональных элементов при высоких отношениях сигнал/шум.
На рис. 5 приведены результаты расчёта вероятности правильного определения границы для морфологии А и морфологии F . Расчёт значений P co производился по следующей формуле [15]:
P = .TP .
max { N , N b }
где N I и N B – число точек контура в эталонном и полученном РКП изображениях соответственно.
Сравнивая поведения P ˆ co для эталонных изображений, построенных на основе морфологии типа А или F (рис. 5), видно, что графики, описывающие P ˆ co для различных реализаций алгоритмов оконтуривания, имеют общую тенденцию. Анализируя вероятность правильного обнаружения P ˆ co для изображений, полученных на основе морфологии типа A , можно отметить, что реализация алгоритма Canny даёт наихудшие результаты практически для всех соотношений сигнал/шум. Имплементация алгоритма Marr-Hildreth на всём промежутке отношений сигнал/шум превосходит алгоритм Canny и уступает реализации ISEF на промежутке сигнал/шум < 32 дБ.
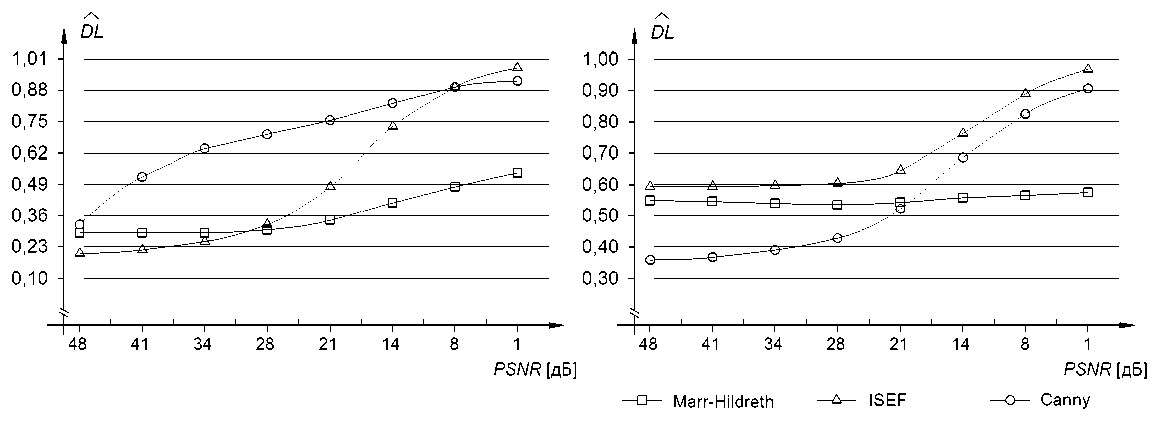
Рис. 4. Обобщённый показатель качества для морфологии типа A , F (справа)
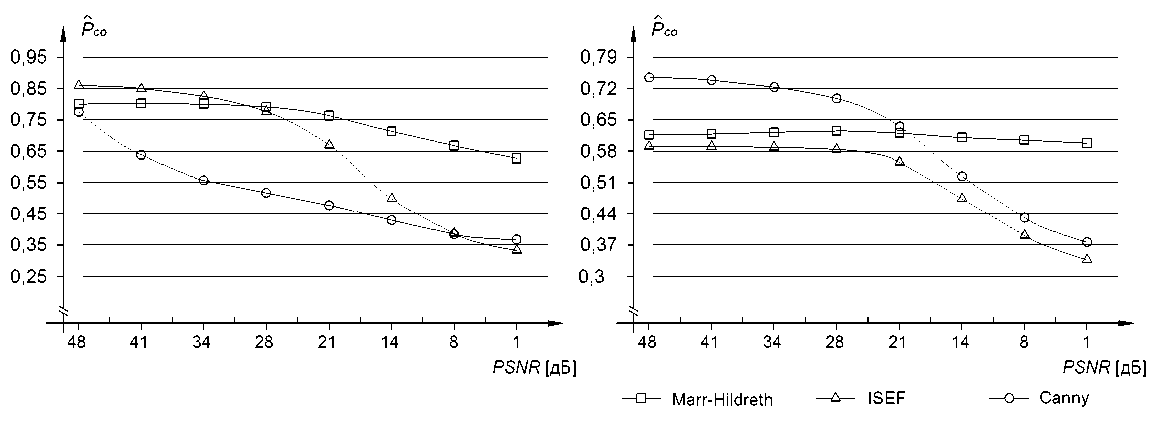
Рис. 5. P co для эталонных изображений морфологии A , F (справа)
Сравнивая вероятности правильного обнаружения P ˆ co для изображений, полученных на основе морфологии типа F , видно, что реализация алгоритма ISEF даёт наихудшие результаты на всём промежутке отношений сигнал/шум. Оператор Canny значительно превосходит оператор Marr-Hildreth при отношениях сигнал/шум больших 20 дБ, а при отношениях сиг-нал/шум > 18 дБ он сопоставим с оператором ISEF.
На рис. 6 приведены оценки вероятности пропуска границы. Расчёт значений P nd производился по формуле [15]
P = FN nd max { N i , N b }
Сравнивая вероятности пропуска границы Pnd для изображений, полученных на основе морфологии типа A, видно, что алгоритм Canny даёт наихудшие результаты практически на всём промежутке отношений сигнал/шум. Алгоритм Marr-Hildreth при отношениях сигнал/шум больших 30 дБ допускает меньшее количество ошибок первого рода, чем Canny, но качественно уступает оператору ISEF. В случае морфологии типа F, на промежутке отношений сигнал/шум больших 20 дБ алгоритм ISEF работает лучше, чем Canny, а в свою очередь алгоритм Canny показывает более хорошие результаты, чем алгоритм Marr-Hildreth. При отношениях сигнал/шум < 16 дБ алгоритм Canny дает наименьшую вероятность пропуска границы.
Оценки вероятностей ложных тревог ( P ˆ fa , ошибки второго рода) были рассчитаны по формуле [15]
A
P fa =
FP max { Ni , Nb }
Результаты расчета соответственно для морфологий типа A и F представлены на рис. 7. Видно, что алгоритм Canny практически на всём промежутке отношений сигнал/шум даёт наихудшие результаты. Алгоритм ISEF при отношениях сигнал/шум больших 30 дБ допускает самое малое количество ошибок второго рода, а при отношениях сигнал/шум меньших 30 дБ уже самым эффективным является оператор Marr-Hildreth.
Анализируя вероятности ложных тревог P ˆ fa для изображений, полученных на основе морфологии типа F , можно отметить, что реализация алгоритма ISEF даёт наихудшие результаты на всём промежутке отношений сигнал/шум. Реализация алгоритма Canny при отношениях сигнал/шум больших 22 дБ допускает меньшее количество ошибок второго рода, чем реализация алгоритма Marr-Hildreth.
На практике нередко возникают вопросы, связанные с качеством детектирования отдельных элементов РКП или их определённых комбинаций. В качестве примера на рис. 8 приведены оценки вероятности правильного обнаружения 170-го элемента алфавита морфологии типа A и 85-го элемента алфавита морфологии типа F , рассчитанные на программном комплексе «КИМ СП» [18].
Возможен и более детальный анализ поведения реализации исследуемых алгоритмов. Например, на рис. 9 приведены графики зависимостей величины отношения ошибок детектирования первого рода ЭПВС, созданных на основе морфологии F , к аналогичной ошибке детектирования ЭПВС морфологии A от уровня PSNR .
Из данных графиков видно, что реализации алгоритмов детектирования по-разному выделяют гори-зонтальные/вертикальные и диагональные участки границ. Например, алгоритм Canny в 1,5 раза лучше проводит локализацию диагональных элементов. Причём максимум оценки получен при отношениях сигнал/шум равных 31 дБ. С другой стороны, реализация алгоритма ISEF детектирует горизонтальные и вертикальные элементы растрового контурного поля морфологии A в 2,9 раза лучше, чем элементы РКП морфологии F . Максимум оценки приходится на 48 дБ.
На рис. 10 приведены результаты детектирования подобных элементов (17-й и 68-й элементы алфавита морфологии типа F ). Из графиков видно, что оба элемента морфологии первой группы [18] детектируются в целом соразмерно. Разброс значений отношения вероятностей пропуска границы для различных реализаций операторов поиска и локализации границ лежит в интервале 6 %.
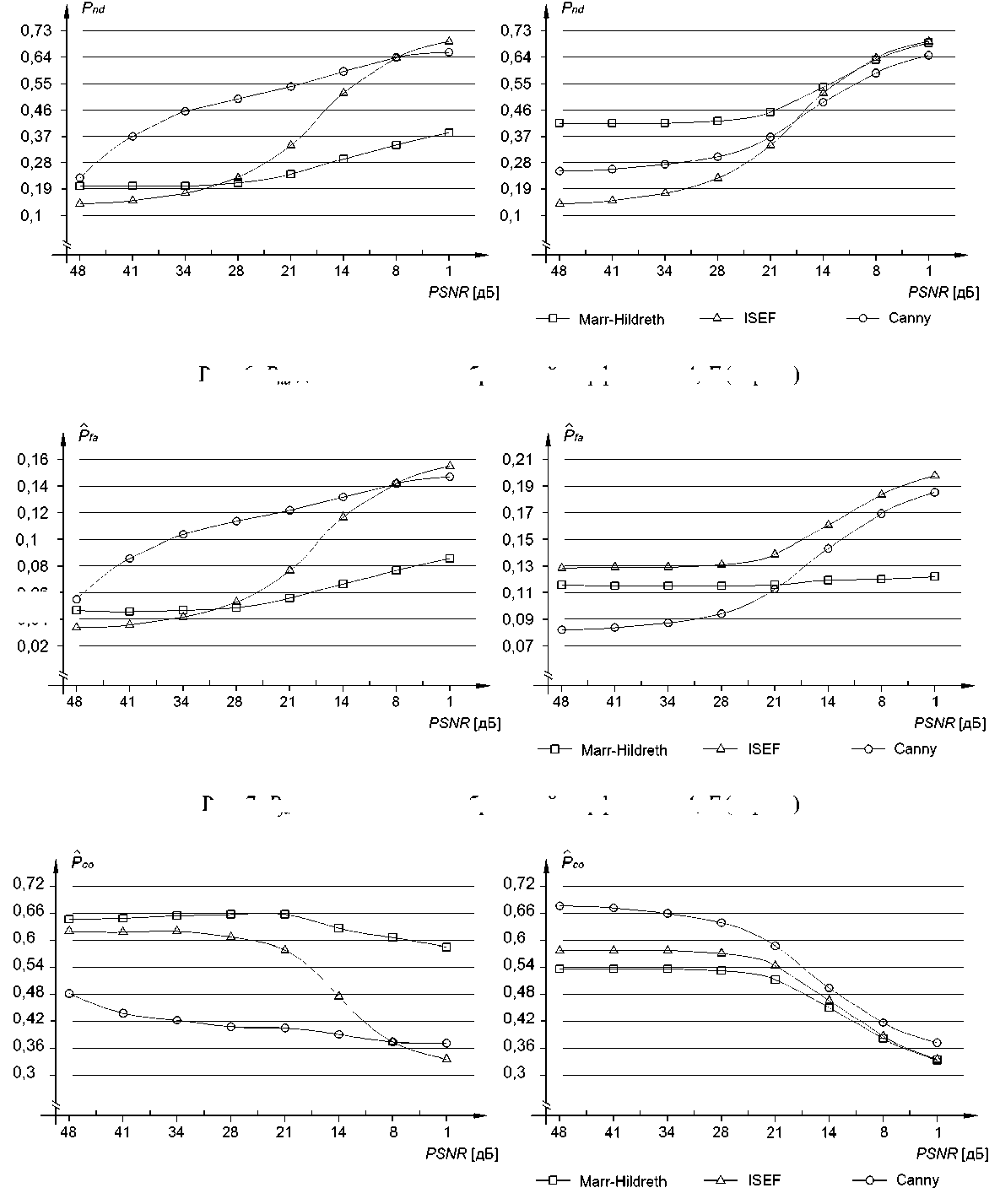
Рис. 6. P nd для эталонных изображений морфологии A , F (справа)
0,06 -
0,04 -
Рис. 7. P fa для эталонных изображений морфологии А , F (справа)
Рис. 8. P co для элементов 170 морфологии А и 85 морфологии F (справа)
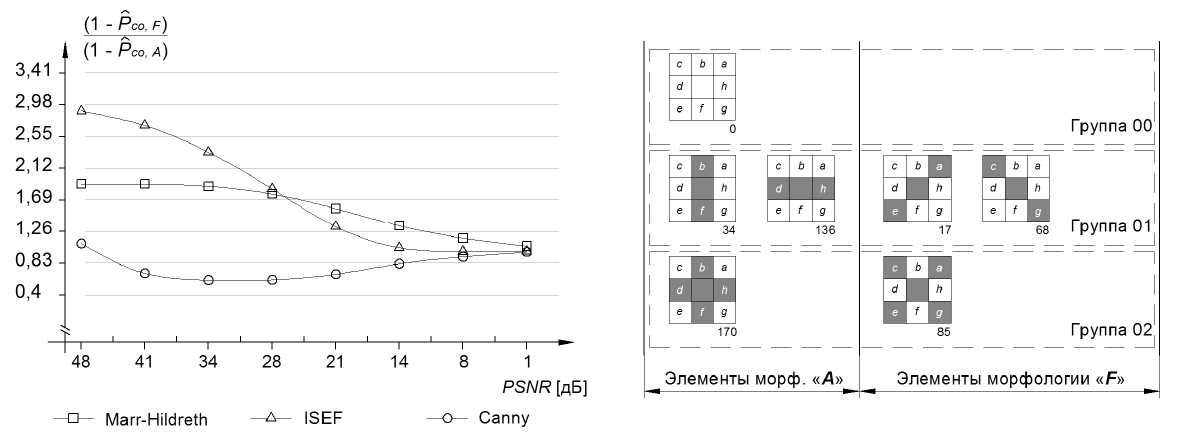
Рис. 9. Отношение оценок вероятностей пропуска границы для морфологий А и F
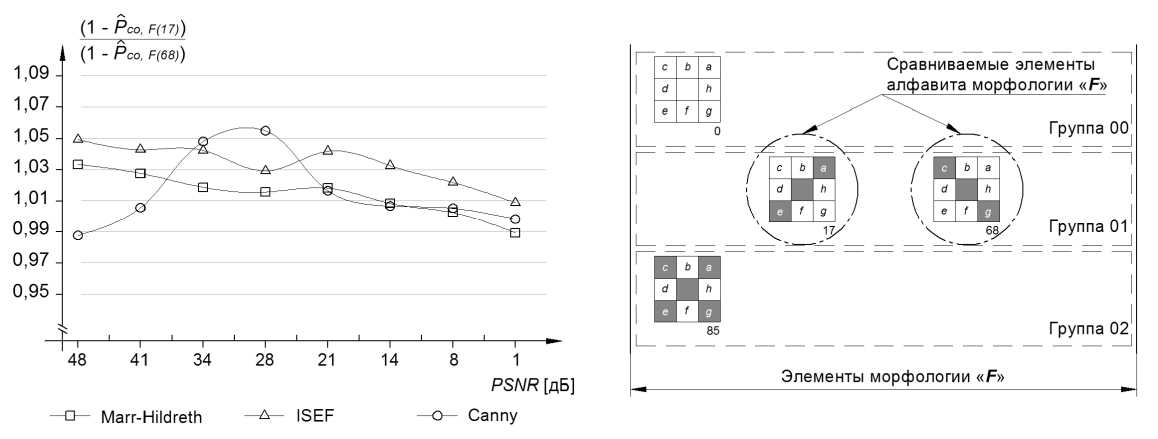
Рис. 10. Отношение оценок вероятностей пропуска границы для морфологий F (элемент 17 и элемент 68)
Дальнейшие исследования связаны с оценками качества детектирования границ для других разновидностей морфологий ( B , C , D , E , FB , FC , FD , FE ), для малоконтрастных реализаций ЭПВС, а также для различных типов границ. Интерес представляет зависимость оценки качества локализации от входных параметров контурных детекторов для различных отношений сигнал/шум и оценка чувствительности контурных детекторов.
Заключение. Таким образом, полученные результаты численных экспериментов на программноалгоритмическом комплексе «КИМ СП» показали, что метод, предложенный в [15], может быть использован для объективной оценки качества алгоритмов поиска и локализации границ. Проведенные исследования на примере трех известных алгоритмов детектирования (Marr-Hildreth, ISEF, Canny) по данному методу позволили выделить области предпочтения каждого из алгоритмов в зависимости от отношения сигнал/ шум и типа морфологии, лежащей в основе построения изображения.
Существует, на наш взгляд, и ряд недостатков метода, основным из которых является попытка использования метрики Пратта для оценки вероятности обнаружения границ, что приводит к статистической зависимости отдельных метрик в обобщенном показателе качества DL. Также имеется сложность интерпретации полученных результатов с точки зрения требований функциональной эффективности проектируемой системы.
С целью проведения дальнейших исследований будет проведена доработка специального математического и программного обеспечения комплекса «КИМ СП» для принятия рациональных решений на основе экспертных оценок и оптимизации обработки информации.
Список литературы Результаты исследования комплексного метода оценки качества оконтуривания на основе двухмерного точечного потока восстановления
- G. Liu, R. Haralick Optimal matching problem in detection and recognition performance evaluation//Journal of the Pattern Recognition Society. 2002. Vol. 35. P. 2125-2139.
- Kanga C., Wang W. A novel edge detection method based on the maximizing objective function//Journal of the Pattern Recognition Society. 2007. Vol. 40. P. 609-618.
- Generation of fuzzy edge images using trapezoidal membership functions/C. Lopez-Molina . France: Atlantis Publisher, 2011. P. 327-333.
- Лаевский В. Е. Методика субоптимальной оценки работы алгоритмов получения контурного рисунка изображений//Известия Томского политехнического университета. 2009. Т. 314, № 5. С. 126-131.
- Лаевский В. Е., Денисов В. П., Дубинин Д. В. Имитационное моделирование: Исследование алгоритмов оконтуривания объектов в изображениях. Saarbrücken: LAP LAMBERT Academic Publishing GmbH & Co. KG, 2011. 123 с.
- Дубинин Д. В., Лаевский В. Е., Кочегуров А. И. Оценка качества алгоритмов оконтуривания объектов на изображениях, аппроксимированных однородными марковскими полями//Известия Томского политехнического университета. 2010. Т. 317, № 5. С. 130-134.
- Дубинин Д. В., Кочегуров А. И., Лаевский В. Е. Методика моделирования случайных яркостных полей, аппроксимированных однородными одноуровневыми марковскими цепями//Проблемы информатики. 2011. № 4(12). С. 35-40.
- Dubinin D., Geringer V., Kochegurov A. Eine Methode zur Erzeugung stochastischer Helligkeits -felder durch homogene, einstufige Markoff-Ketten, tm -Technisches Messen. Oldenbourg, 2012. № 5. Р. 271-276.
- Abdou I. A., Pratt W. Quantitative Design and Evaluation of Enhancement//Thresholding Edge Detectors: Proceedings of the IEEE. 1979. Vol. 67, № 5. P. 753-763.
- Kitchen L., Rosenfeld A. Edge Evaluation Using Local Edge Coherence//IEEE Transactions on Systems. 1981. Vol. 11, № 9. P. 597-605.
- Venkatesh S., Kitchen L. Edge Evaluation Using Necessary Components//Computer Vision, Graphics, and Image Processing. 1992. Vol. 54, № 1. P. 23-30.
- Salotti M., Bellet F., Garbay C. Evaluation of Edge Detectors: Critics and Proposal//Proceed of the ECCV Workshop on Performance Characteristics of Vision Algorithms. 1996.
- An efficient Method to Evaluate the Performance of Edge Detection Techniques by a two-dimensional Semi-Markov Model/D. Dubinin //IEEE Symposium on Computational Intelligence in Control and Automation (CICA 2014). USA, Florida, Orlando, CICA: IEEE Press, 2014. P. 1-7, DOI 10.1109/CICA.2014. 7013248.
- Lopez-Molina C., De Baets B., Bustince H. Quantitative error measures for edge detection//Pattern Recognition. 2013. Vol. 46, № 4. P. 1125-1139.
- Boaventura I., Gonzaga A. Method to Evaluate the Performance of Edge Detector//SIBGRAPI 2009: XXIInd Brazilian Symposium on Computer Graphics and Image Processing. Rio de Janeiro, 2009. P. 1-3.
- Edge detection: A statistical approach/A. Halder //Electronics Computer Technology (ICECT): 3rd International Conference. 2011. Vol. 2. P. 306-309.
- Bundled Software for Simulation Modeling/D. Dubinin //Proceedings of the International Symposium on Signals, Circuits and Systems (ISSCS 2013). Romania, Iasi: ISSCS Press (IEEE Catalog Number: CFP13816-CDR), 2013. P. 1-4.
- Ein stochastischer Algorithmus zur Bildgenerierung durch einen zweidimensionalen Markoff-Erneuerungsprozess/D. Dubinin //Oldenbourg Wissenschaftsverlag. 2014. Heft 62 (1). Р. 57-64.
- Дубинин Д. В., Кочегуров А. И., Лаевский В. Е. К статистике морфологии случайных пространственновременных сигналов, сформированных двумерным точечным потоком восстановления//Известия Томского политехнического университета. 2012. Т. 321, № 5. C. 194-198.
- Yates J. Contingency table involving small numbers and the χ2 test//Royal Statistical Society. 1934. Vol. 1. P. 217-235.
- Marr D., Hildreth E. Theory of Edge Detection//In Proceedings of the Royal Society of London. 1980. B 207. P. 187-217.
- Shen J., Castan S. An optimal linear operator for edge detection//IEEE Proceedings of the Conference on Vision and Pattern Recognition. 1986. P. 109-114.
- Canny J. A Computational Approach to Edge Detection//IEEE Trans. Pattern Analysis and Machine Intelligence. 1986. Vol. 8, № 6. P. 679-698.
- Liu G., Haralick R. Optimal matching problem in detection and recognition performance evaluation, Journal of the Pattern Recognition Society, 2002, Vol. 35, P. 2125-2139.
- Kanga C., Wang W. A novel edge detection method based on the maximizing objective function. Journal of the Pattern Recognition Society, ELSEVIER Publ., 2007, Vol. 40, P. 609-618.
- Lopez-Molina C. et al. Generation of fuzzy edge images using trapezoidal membership functions, France: Atlantis Publ., 2011, P. 327-333.
- Laevski V. E. . Izvestiya Tomskogo politekhnicheskogo universiteta. 2009, Vol. 314, No. 5, P. 126-131 (In Russ.).
- Laevskiy V. E., Denisov V. P., Dubinin D. V. Imitatsionnoe modelirovanie: Issledovanie algoritmov okonturivaniya ob’ektov v izobrazheniyakh . LAP-LAMBERT Academic Publ., Saarbrücken, 2011, 123 p.
- Dubinin D. V., Laevskiy V. E., Kochegurov A. I. . Izvestiya Tomskogo politekhnicheskogo universiteta. 2010, Vol. 317, No. 5, P. 130-134 (In Russ.).
- Dubinin D. V., Kochegurov A. I., Laevskiy V. E. . Problemy informatiki, 2011, No. 4(12), P. 35-40 (In Russ.).
- Dubinin D., Geringer V., Kochegurov A. A particular method of modelling stochastic intensity fields by isotropic, one-step Markov chains. Eine Methode zur Erzeugung stochastischer Helligkeitsfelder durch homogene, einstufige Markoff-Ketten. tm -Technisches Messen, Oldenbourg: Scientific Publ., 2012, No. 5, P. 271-276.
- Abdou I. A., Pratt W. Quantitative Design and Evaluation of Enhancement. Thresholding Edge Detectors. Proceedings of the IEEE, 1979, Vol. 67, No. 5, P. 753-763.
- Kitchen L., Rosenfeld A. Edge Evaluation Using Local Edge Coherence. IEEE Transactions on Systems, 1981, Vol. 11, No. 9, P. 597-605.
- Venkatesh S., Kitchen L. Edge Evaluation Using Necessary Components. Computer Vision, Graphics, and Image Processing, 1992, Vol. 54, No. 1, P. 23-30.
- Salotti M., Bellet F., Garbay C. Evaluation of Edge Detectors: Critics and Proposal. In: Proceed of the ECCV Workshop on Performance Characteristics of Vision Algorithms. 1996.
- Dubinin D., Geringer V., Kochegurov A., Reif K. An efficient Method to Evaluate the Performance of Edge Detection Techniques by a two-dimensional Semi-Markov Model. IEEE Symposium on Computational Intelligence in Control and Automation (CICA 2014), USA, Florida, Orlando, CICA: IEEE Press, 2014, P. 1-7, DOI 10.1109/CICA.2014.7013248.
- Lopez-Molina C., De Baets B., Bustince H. Quantitative error measures for edge detection. Pattern Recognition, 2013, Vol. 46, No. 4, P. 1125-1139.
- Boaventura I., Gonzaga A. Method to Evaluate the Performance of Edge Detector. SIBGRAPI 2009, XXIInd Brazilian Symposium on Computer Graphics and Image Processing, Rio de Janeiro, 2009, P. 1-3.
- Halder A., Chatterjee N., Kar A., Pal S., Pramanik S. Edge detection: A statistical approach. Electronics Computer Technology (ICECT), 2011. 3rd International Conference, 2011, Vol. 2, P. 306-309.
- Dubinin D., Geringer V., Kochegurov A., Reif K. Bundled Software for Simulation Modeling. Proceedings of the International Symposium on Signals, Circuits and Systems (ISSCS 2013), Romania, Iasi: ISSCS Press (IEEE Catalog Number: CFP13816-CDR), 2013, P. 1-4.
- Dubinin D., Geringer V., Kochegurov A., Reif K. A stochastic algorithm for generating images by a two-dimensional Semi-Markov Model. . Oldenbourg Wissenschaftsverlag, Automatisierungstechnik, 2014. Heft 62 (1), P. 57-64.
- Dubinin D., Kochegurov A., Laevski V. (Geringer V.) . Izvestiya Tomskogo politekhnicheskogo universiteta, 2012, Vol. 321, No. 5, P. 194-198 (In Russ.).
- Yates J. Contingency table involving small numbers and the χ2 test, Royal Statistical Society, 1934, Vol. 1, P. 217-235.
- Marr D., Hildreth E. Theory of Edge Detection. In Proceedings of the Royal Society of London, B 207, 1980, P. 187-217.
- Shen J., Castan S. An optimal linear operator for edge detection. IEEE Proceedings of the Conference on Vision and Pattern Recognition, 1986, P. 109-114.
- Canny J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Analysis and Machine Intelligence, 1986, Vol. 8, No. 6, P. 679-698.


