Робастная нелинейная система возбуждения синхронного генератора: интегральная адаптация

Современные сложные технические объекты и системы функционируют в условиях существенной неопределённости внутренней и внешней среды. Более того, эти условия могут носить экстремальный характер, угрожающий нормальному функционированию соответствующего технического объекта или его подсистем. К таким объектам, в частности, относятся синхронные генераторы (СГ) энергосистем. На СГ постоянно действуют внешние возмущения, зачастую выводящие систему далеко от номинального режима. Например, резкие скачки потребляемой мощности, замыкания на линиях электропередач или их обрыв и т. п. В СГ неопределённость внутренней среды связана с текущим изменением параметров его подсистем. Указанные параметры могут изменяться как в определённых интервалах, не приводящих к нарушению технологических режимов объектов, так и выходить за допустимые диапазоны, приводящие к аварийным условиям функционирования указанных сложных объектов и их подсистем. Это приводит нас к пониманию проблемы синтеза робастных законов управления и определяет необходимость построения адаптивных систем управления с целью повышения устойчивости системы возбуждения СГ за счёт уменьшения неопределённостей реального процесса (адаптивности к изменению параметров и действию внешних возмущений).

Обзор состояния в области адаптивного управления энергосистемами. Для линейных систем адаптивное управление, как правило, строится в соответствии с классическими методами линейной теории адаптивного управления [5‒8]. Но традиционный подход, основанный на линейных моделях объектов энергосистем, пригоден лишь в режимах номинальной работы энергосистемы, так как линеаризованная модель является адекватной только в области малых отклонений от номинального режима. В [9] отмечается, что для энергосистем использование линейных регуляторов не может гарантировать устойчивость исходной нелинейной энергосистемы, подверженной внешним и параметрическим возмущениям. В настоящее время адаптивность и робастность систем управления обеспечивается за счёт совместного использования традиционных линейных регуляторов и методов H_m -управления, методов теории нечётких систем управления или искусственных нейронных сетей. Однако в нечётких системах возникает проблема «проклятия размерности» — число правил пропорционально степени числа входных переменных (размерности системы). Это в свою очередь ведёт к «трудности восприятия и объяснения». К тому же «в большинстве работ настройки [линейных] регуляторов выбираются на основании опытных знаний экспертов, общих представлений о физике протекания процессов или методом проб и ошибок. Подобный подход не гарантирует нахождения оптимальных настроек регулятора и в сильной степени зависит от человеческого фактора» [1].

В [9‒11] к современным нелинейным методам теории управления, используемым для построения робастных систем управления объектами энергосистем, в том числе систем возбуждения СГ, относятся прямой метод Ляпунова, метод линеаризации обратной связью, метод пассифика-ции, метод энергетических функций др. Авторы предлагают использовать скользящие режимы для обеспечения робастности энергосистемы к возмущениям [9].

Синерго-кибернетический подход базируется на обеспечении устойчивости движения объекта за счёт соответствующего синтеза нелинейных законов робастного управления, обеспечивающих максимальную область асимптотической устойчивости замкнутой системы «гарантирующий регулятор — объект». Для решения данной задачи синтеза следует применять основной метод синергетической теории управления (СТУ) — метод аналитического конструирования агрегированных регуляторов (АКАР), развитый научной школой Южного федерального университета и нашедший обширное применение в различных областях современной техники — авиации, энергетике, электромеханике и т. д. [1‒4, 12].

Для реализации системно-кибернетического подхода к построению робастных систем управления СТУ предлагает следующие основные подходы [1‒4]:

• 1)    для идентификации параметрических и/или внешних возмущений применяются соответствующие синергетические нелинейные наблюдатели возмущений (ННВ). В этом случае синтезируемые методом АКАР законы управления дополняются подсистемой наблюдения, осуществляющей динамическую оценку неизмеряемых возмущений и их подавление. Более подробно использование ННВ для объектов энергосистем представлено в [1, 13, 14];

• 2)    использование принципа интегральной адаптации, когда влияние параметрических и/или внешних возмущений на функционирование системы подавляется за счёт построенных нелинейных законов управления с особым образом введёнными интеграторами.

Постановка задачи и синтез закона управления. В данной работе выполнен синтез нелинейного адаптивного закона управления возбуждением СГ, обеспечивающего:

• •    заданное напряжение на выводах СГ U t = U 0 и его синхронизм в номинальном режиме работы

ш = Ш о ;

• •    возврат СГ в номинальный режим после аварийных ситуаций, вызванных возмущениями;

• •    устойчивость работы СГ при параметрическом возмущении.

В качестве объекта управления рассматривалась модель СГ, работающего на систему неограниченной мощности с чисто активной нагрузкой, которая в относительных единицах в системе синхронно вращающихся осей d, q имеет вид x (t) = -c1 x1 + с2x3 + с3x4x2 + с4 sin x5 - f1 x1M + f2x3M;

x ₂ ( t ) = с 3 x 4 x 1 - с 5 x ₂ - с 4 cos x 5 - f ₃ x ₂ M ;

^x 3 ( t ) = ^{- c} 6 ^x 3 + c 7 ^x 1 + b 1 u;                                       (1)

x 4 ( t ) = c 8 - c 9 x 3 x 2 + c 10 ^x 1 x 2 - c 11 x 4 ;

x5 (t) = x4 - Ш0, где x1, x2 — потокосцепление по оси d и q соответственно; x3 — ЭДС ротора СГ; x4 — частота вращения ротора; x5 — электрический угол СГ; M — параметрическое возмущение, выражающееся в изменении сопротивления линии электропередачи; b1,ci,fj — постоянные параметры; u — ЭДС возбуждения СГ, которая в данной модели является управлением [15].

В основе синтеза требуемого закона управления для (1) был использован принцип интегральной адаптации, основанный на методе АКАР синергетической теории управления [1‒4]. При этом полагалось, что параметрическое возмущение — это кусочно-постоянная функция с неизвестной заранее амплитудой. В соответствии с принципом интегральной адаптации необходимо расширить исходную модель (1) дополнительным дифференциальным уравнением — моделью кусочно-постоянного возмущения, в структуру которого входит желаемый инвариант:

z ( t ) = a ( U t - U 0 ) + в ( x 4 - ш ) ,                                    (2)

здесь α, β — постоянные параметры.

Правая часть уравнения (2) структурно представляет собой желаемый технологический инвариант — постоянное желаемое значение терминального напряжения, которое описывается выражением [15]:

Ut = V U + ud, где Ud = -U„ sin x5 + s1 x1 - s2x3, Uq = U„ cos x5 + s3x2.

Расширенную модель СГ получим, добавив уравнение (2) в (1) и заменив слагаемые с M на z :

x 1 ( t ) = - c 1 x 1 + с ₂ x ₃ + с ₃ x ₄ x ₂ + с 4 sin x 5 + z ;

x- 2 ( t ) = с ₃ x 4 x 1 - с ₅ x ₂ - с 4 cos x 5 + z ;

^^ 3 ( t ) = ^{- c} 6 ^x 3 ⁺ c 7 ^x i ⁺ b i u ;                                          (3)

^^ 4 ( t ) = c 8 ^- c 9 ^x 3 ^x 2 ⁺ c io ^x i ^x 2 ^- c ii ^x 4 ;

-x 5 ( t ) = ^x 4 ^{- ш} о ;

;? (t) = a (Ut - U0) + p (x4 - too), где U0 , ω0 — постоянное желаемое значение терминального напряжения и номинальная частота вращения ротора соответственно.

Согласно процедуре метода АКАР составляется макропеременная, реализующая желаемый технологический инвариант:

Ф = a ( U t - U 0 ) + в ( x 4 - to o ) + y z ,                                   (4)

здесь γ — постоянный параметр.

Вводим основное функциональное уравнение метода АКАР T ip ( t ) + Ф = 0,

которое запишем с учётом (4) и (3). Разрешив (5) относительно управления u , получим искомое управление:

1 s ₂ b ₁

- U „ ( cos x 5 + sin x 5 ) ( x 4 - w₀ ) + s 3 ( c 3 x 4 x 1 - c 5 x 2 - c 4 cos x 5 + z ) +

+ S 1 ( - c 1 x 1 + c 2 x 3 + c 3 x 4 x 2 + c 4 sin x 5 + z ) + s 2 c 6 x 3 - s 2 c 7 x 1 +

⁺ ^ ^в ( c 8 - c 9 x 3 x 2 ⁺ c 10 x 1 x 2 - c 11 x 4 ) ⁺ U Y ( ^a ( U t - U 0 ) ^{+ в} ( x 4 - “ 0 ) ) ⁺

+ U T ( a ( U t - U 0 ) + p ( ^x 4 - to o ) + Y z )

здесь z — динамическая переменная, получаемая из (2):

^z = f ( k ( ^Ut ^{- U} 0 ) ^{+ k} 2 ( ^x 4 ^- “ 0 ) ) d .

Для выполнения численного моделирования использовалась среда MATLAB. Для качественной демонстрации закона (6) было произведено моделирование замкнутой системы (3) с ПИД-регулятором:

u = k A U + k — + k f A Udt , p d dt i

где A U = U_t - U ₀ — отклонение терминального напряжения от заданного. Параметры настройки регулятора (7) были получены с помощью утилиты Simulink Response Optimization пакета MATLAB для исходной нелинейной системы (1) по желаемому переходному процессу терминального напряжения.

Параметры системы (1): с 1 = 10,516; c ₂ = 16,529; c ₃ = 376,14; c 4 = 358,14; c ₅ = 28,465; c ₆ = 1,176; c ₇ = 1,007; c ₈ = 0,211; c ₉ = 0,864; c ₁₀ = 0,732; c 11 = 0,021; f 1 = 441,47; f ₂ = 742,15; f ₃ = 1414,6; U „= 0,95; s 1 = 0,023; s ₂ = 0,039; s ₃ = 0,074; а параметры законов управления (6), (7): в = - 24; у = 0,125; k = к 1 = 1; к₂ = 2; U ₀ = 1; м₀ = 1; a = 1,5; T = 0,001; k p = 1; k i = k_d = 80.

На рис. 1‒4 представлены результаты моделирования замкнутой системы (1) с различными законами управления. На графиках сплошной линией показаны результаты моделирования с синергетическим законом управления (6), а пунктирной линией — с законом (7). При моделировании замкнутой системы действует параметрическое возмущение M , моделирующее короткое замыкание на линии [13]:

0,

t <  5;

M = ^

- 0,02, 5 <  t <  5,2;

0,012, t >  5,2.

На основе данных моделирования можно сделать вывод, что синтезированный синергетический закон (6) полностью выполняет предъявляемые к нему требования. Кроме того, он позволяет выдерживать заданный режим СГ, затрачивая меньше энергии, что видно из рис. 4. Синергетический закон способен обеспечить более быстрое гашение параметрических возмущений, нежели классический ПИД-регулятор, при этом отсутствуют колебания терминального напряжения и частоты вращения ротора в переходном режиме.

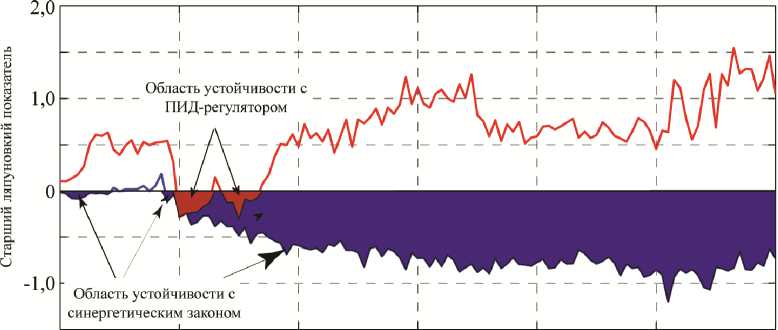
В силу того, что при синтезе закона (6) использовались уравнения исходной системы (3), он способен обеспечивать устойчивость системы при больших значениях возмущения по сравнению с ПИД-регулятором. Для анализа устойчивости произведем расчёт старшего показателя Ля- пунова при различных значениях возмущения M . Как известно, показатели Ляпунова являются численной оценкой эволюции малого возмущения в пространстве состояния системы [16]. Следовательно, если самый большой из спектра показателей Ляпунова является отрицательным, то и все остальные показатели будут отрицательными. Из чего следует, что возмущения в системе угасают по всем направлениям. Это говорит об устойчивости синтезированной системы [16].

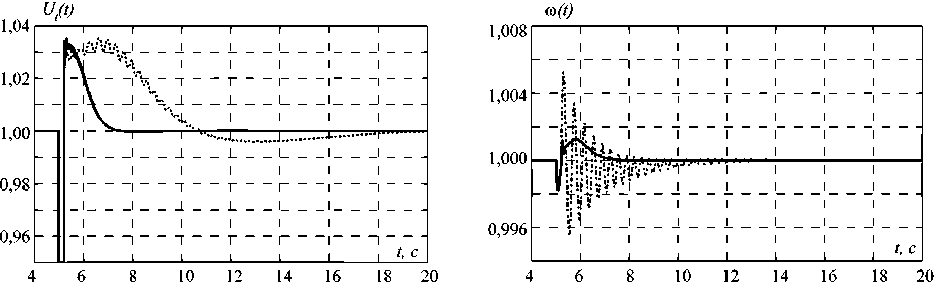
Рис. 1. Терминальное напряжение СГ

Рис. 2. Частота вращения ротора СГ

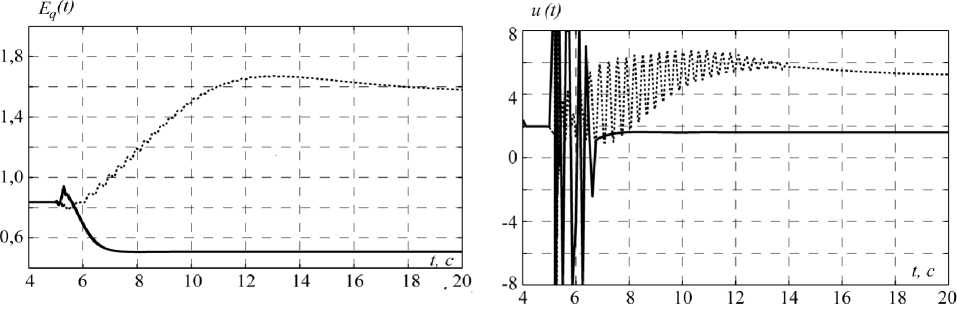
Рис. 4. ЭДС возбуждения СГ — управление

Рис. 3. ЭДС ротора СГ

На рис. 5 показаны графики изменения старшего показателя Ляпунова для исходной системы (1) с синергетическим законом (6) и ПИД-регулятором (7). Для устойчивости системы требуется, чтобы старший показатель принимал отрицательное значение. Из рис. 5 видно, что синергетический закон обеспечивает значительно большую область устойчивости, чем ПИД-регулятор (7).

■0,02           0           0,02          0,04          0,06          0,08           0,1

Возмущение

Рис. 5. Область устойчивости системы (1)

Заключение. Синтез методом АКАР на основе введения инвариантных многообразий в систему, вкупе с введением интегральной составляющей для подавления возмущений, предоставляет возможность синтезировать законы, обеспечивающие более точное, быстрое, экономичное, а главное — надёжное управление, нежели классические линейные законы. В целом, это обеспечивает повышение устойчивости энергосистемы.