Робастное управление космическим роботом-манипулятором при обслуживании геостационарного спутника связи

В противовес многоярусным низкоорбитальным космическим системам связи традиционная космическая связь планирует своё развитие на основе геостационарных платформ, которые собираются на орбите космическими роботами-манипуляторами (КРМ) из сменных и пополняемых компонентов, а затем регулярно обслуживаются КРМ в течение нескольких десятилетий.

В системе управления движением (СУД) КРМ применяются кластер четырёх гиродинов (ГД) и электрореактивные двигательные установки (ЭДУ) на основе как плазменных, так и каталитических электрореактивных двигателей (ЭРД) [1,2]. Измерение координат КРМ выполняется бесплатформенной инерциальной навигационной системой (БИНС) с коррекцией сигналами

от навигационных спутников GPS/ ГЛОНАСС и звездных датчиков. В результате стыковки КРМ с геостационарным спутником связи (ГСС) [3,4] обеспечивается их жесткое соединение, когда возможно удобное техническое обслуживание ГСС с помощью бортового манипулятора робота.

В статье рассматриваются вопросы пространственной стабилизации связки КРМ с ГСС в орбитальной системе координат (ОСК) при техническом обслуживании ГСС – замены топливных баков ЭДУ, панелей солнечных батарей (СБ), аккумуляторов бортовой системы электропитания и других сменяемых компонентов служебного модуля СУД. При таких механических перемещениях существенно изменяются как положение центра масс, так и значение тензора инерции связки.

Цель статьи состоит в обеспечении робастности СУД КРМ – слабой зависимости показателей качества её работы от изменения инерционных свойств жёсткой связки КРМ и ГСС. Определяются требования к электромеханическим приводам СУД робота, его манипулятора и представляются результаты компьютерной имитации динамических процессов.

ПОСТАНОВКА ЗАДАЧИ

В работе [2] авторы исследовали динамику СУД КРМ при смене топливных баков ЭДУ ГСС, где предполагалось, что КРМ и ГСС жестко состыкованы и механические манипуляции со сменными топливными баками массой 90 кг происходят в автоматическом режиме. На рисунке 1 приведены используемые формы и размеры (в метрах) механической связки КРМ с ГСС, для компактности без отображения панелей СБ, а рис. 2 представляет кинематическую схему бортового манипулятора антропоморфной структуры с 4 звеньями (i = 1,2,...4 = 1 ^ 4) и 6 степенями свободы, которым соответствуют угловые координаты qs, s = 1 ^ 6. Здесь указаны концы звеньев манипулятора в точках А, B, C и концевая точка D ключа замкового механизма. В точках А и С применяются двухстепенные шарниры, которые однозначно формализуются двумя стандартными одноосными шарнирами при значениях длины фиктивных звеньев lci = lоз = О, рис. 2. Последний шарнир обеспечивает вращение ключа замкового механизма, а остальные – совмещение точки С манипулятора с заданной точкой при произвольной ориентации последнего звена. Манипулятор закреплен на корпусе КРМ стойкой (master) в начале Om системы координат Omxmymzm , которая фиксирована в системе координат Orxryrzr робота в его центре масс Or, см. рис. 1.

Применяемая в [2] стратегия смены топливных баков ЭДУ использовала такие положения:

• 1)    пустые баки поочередно перемещаются манипулятором из контейнеров ГСС в контейнеры КРМ, а заполненные топливом баки – наоборот, из контейнеров КРМ в контейнеры ГСС;

• 2)    установка баков в контейнеры завершается их автоматической механической фиксацией;

• 3)    включение /отключение системы подачи

топлива от каждого бака к ЭДУ осуществляется роботизированным мехатронным модулем, встроенным в каждый контейнер ГСС.

При математическом описании движения механической связки КРМ с ГСС применяются (i) экваториальная инерциальная системы координат (ИСК) I _е с началом в центре Земли O _e , (ii) связанная система координат (ССК) B (О xyz ) с началом в полюсе O , которая совпадает с системой координат O _r x _r y _r z _r КРМ; (iii) орбитальная система координат (ОСК) O (O x ^o y ^o z ^o) с началом в полюсе O и ортами r o , T o , n o , которая имеет следующие направления осей и ортов: ось O x ^o направлена по радиали r ^o , ось O z ^o – по нормали n ^o к плоскости орбиты, а ось O y ^o – по трансверсали T ⁰ и направлена в сторону орбитального движения. На рисунке 1 представлена также система координат O _t x _t y _t z _t , связанная с корпусом ГСС (цель, target) в его центре масс O _t . Далее используются обозначения col( - ) = { • } , li^{ne( - )} = ^{[ - ]} , ( ■ , ■ ) , [ х- ], ( - ) t , [ a x ] и ° ,~ для векторов, матриц и кватернионов, а также матриц [ а ] i стандартного элементарного поворота вокруг i -ой оси на угол а , i = 1 ^ 3 .

Для управления ориентацией связки КРМ с ГСС применяется силовой гироскопический кластер (СГК) на основе четырех ГД по схеме 2-SPE с ортами векторов кинетических моментов (КМ) h p ( в p ) , p = 1 ^ 4 , рис. 3, где приведена

+

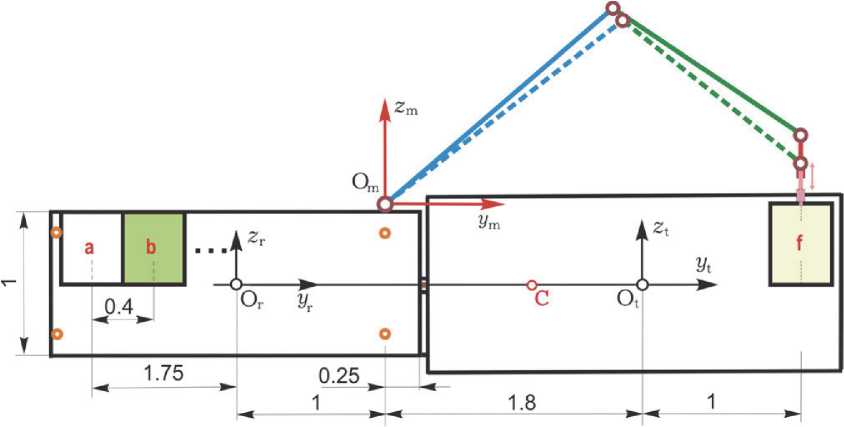
Рис. 1. Схема управления манипулятором при смене топливных баков ЭДУ

Рис. 2. Кинематическая схема бортового манипулятора

также область вариации нормированного вектора КМ h ( e ) = X h p ( р p ) кластера со столбцом в = {Р p } и ее проекции на плоскости гироскопического базиса O x ^g y ^g z g . Применяемый явный закон настройки СГК (распределения вектора его управляющего момента М ^g = {М f } между четырьмя ГД) позволяет исключить избыточность данного кластера с вектором кинетического момента H = h_g h ( P ) , где h_g - одинаковое для всех четырех ГД постоянное значение модуля собственного КМ.

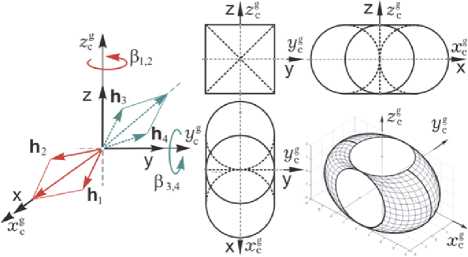
Рис. 3. Схема СГК и область вариации его КМ

Ориентация ССК B в ИСК I @ определяется кватернионом Л = (X0,X), где X = {Xi}, вектором модифицированных параметров Родрига (МПР) ст = {стi} = e tan(Ф /4) с ортом e оси Эйлера и углом Φ собственного поворота. В ИСК I @ кинематические уравнения для вектора rr расположения КРМ, кватерниона Λ и вектора МПР σ имеют вид гг = г' + йхгг;    Л = Л о й/2;

СТ = |(1 -ст ²) й + 1 СТ Х Й +| ( ст , Й > СТ ,    ⁽¹⁾

где вектор ω представляет угловую скорость корпуса КРМ и используется обозначение ( • ) ‘ локальной производной по времени.

Ориентация базиса O относительно базиса I _е определяется кватернионом Л ⁰ , углами рыскания ф 1 = ^ , крена ф ₂ = ф и тангажа ф ₃ =0 в последовательности 132, а также матрицей направляющих косинусов координатного перехода от ОСК к ССК C ⁰ = [ ф ₂ ] ₂ [ ф ₃ ] ₃ [ ф 1 ] 1 .

Погрешность ориентации базиса B в базисе O определяется кватернионом E = Л ⁰ ° Л = ( e ₀ , e ) , где e ₀ = соз( Ф ^е / 2), вектор e = { e i } = cos( Ф ^e /2) e ^e с ортом е ^e оси Эйлера и углом Ф ^е, матрицей C ^e = I ₃ - 2[ e x ] Q t_e , где Q _e = I ₃ e ₀ + [ e x ] , а также вектором угловой погрешности 8ф = { 8ф i } = {2 e ₀ e i } и вектором МПР СТ ^e = { ст e } = e ^e tan( Ф ^e / 4) . При этом вектор S to погрешности по угловой скорости определяется соотношением S to = to — C ^e to ⁰ ( t ) .

При математическом моделировании движения связки КРМ с ГСС применяется векторная форма классических уравнений Эйлера-Лагранжа [5]. В ССК Oxyz с полюсом O векторы Pi, i = 1 ^ 4 определяют положения центров масс ci звеньев манипулятора с массами mi и соб-Jc _____ i, а векторы рг = 0 и рt - положения центров масс Or и Ot робота (индекс r) и цели (индекс t) с массами и собственными тензорами инерции mr, J С и mt, Jc соответственно. Положение центра масс C связки КРМ и ГСС (робот, манипулятор с 4 звеньями и цель, см. рис. 1) суммарной массы m = mr + Emi + mt определяется вектором Pc = {xС, Уc,zС} по соотношению

L = ^m P c = m r P r ^{+ X m} i P i ^{+ m} t P t , где введен вектор статического момента L . Тензор инерции J механической системы в полюсе O вычисляется по соотношению

J < /_y . || = J о + L J о + J о ,        (2)

где при единичном тензоре E имеем

J 0 = J c ; J o = J c + m i ( E P tt P i — P i P t ) ;

При векторе v 0 скорости полюса O поступательное движение связки КРМ с ГСС описывается векторным уравнением mvn -LХй = йх(LХй)-

⁰                                          (3)

-S/(m(2®xp' + p')) + Pe + Fgr, где v0 = v0 +tox v0; Pi = S,( dPi Idqs)qs) ;

P" = Es( dPi/dqs)qs +Xk(d2 Pi Idqk dqs), векторы Pe и Fg представляют силы тяги ЭДУ, центрированной в полюсе O, и гравитации.

Через ω _i обозначим вектор угловой скорости i -го звена манипулятора в ССК. Производная этого вектора по времени имеет вид to i = to i + to x to i . В ССК O xyz с полюсом O вращательное движение связки указанных твердых тел описывается векторным уравнением

L x vn + J(b = -L x (йх vn)

^{0                         0}                    (4)

-йх (Jй + H) - R + Mg + Me + Mgr, где

R = X i ( J 0(b i + to x J 0 to i + to i x J 0 ( to + to i )

+ miPi x (tox (toxPi)+ 2toxPi + Pi"),

векторы M ^g = — H ‘ и M ^e = M представляют управляющие моменты СГК с вектором КМ H и ЭДУ на основе 8 каталитических ЭРД, а вектор M ^gr - гравитационный момент.

Векторные уравнения Эйлера (3), (4) дополняются стандартными уравнениями Лагранжа по степеням подвижности q_s манипулятора, где в правых частях наряду с обобщенными силами

Q_s , представляющими моменты электромеханических приводов, имеются механические моменты [5], которые обусловлены пространственным движением связки КРМ с ГСС.

При цифровом управлении u _к( t ) = {и^ ( t )} СГК с периодом T u , где для k е N₀ г [0,1,2,...) компоненты ^u f ⁽ t ⁾ = ^{и^⁽ t ^)} V t ^{е [} t_k , t_k + 1 ) , t_{k + 1} = t_k + T u формируют вектор управляющего момента СГК

M k ( t ) = - h _g A h ( в ( t ) u g ( t ) ; в ( t ) = u k ( t ) , (5) где матрица Якоби A _h ( в ) = d h ( P ) Zdp .

В процессе угловой стабилизации связки указанных космических аппаратов (КА) в ОСК при законе наведения Ло(t),to0(t), Йo(t) = £o(t) после дискретной фильтрации измеренных значений вектора углового рассогласования £ a г — 5ф l, l е N0 с периодом Tq = Tu /4 формируются значения вектора Ekf, k е N0, которые применяются в алгоритме управления СГК с периодом Tu в виде a a a a af. ~ a a a af gk+1 = Bgk + C £k ’ mk = K (gk + F £k b

M ® = to_k x G_k + J ( C £ 0 + [ c : to 0 x ] to_k + m_k ). к             К

Здесь вектор G _k = J ω _k + H _k и используются постоянные диагональные матрицы K ^a , B ^a , C ^a и P ^a . Далее вектор M k с помощью явного закона распределения команд между четырьмя ГД [6] «пересчитывается» в столбец u k = {u ^ ^k } командных сигналов управления гиродинами, которые фиксируются на полуинтервалах цифрового управления СГК с периодом T_u при формировании его управляющего момента M k ( t ) по соотношениям (5).

Обоснование параметров манипулятора и расчет рабочей зоны при ограничениях

• -    л <  q, < л , 0 <  q ₉< л;

^{1                2}                     (7)

• -    л <  q_z - < л ,    i = 3 + 6

на его угловые координаты подробно представлены в [2]. Здесь с каждым i -ым звеном манипулятора ( i = 1 ^ 4 ) связывается система координат (СК) с началом в точке сопряжения i -ой пары звеньев, см. рис. 2. Кинематическая модель манипулятора включает формулы решения прямой и обратной задачи кинематики [7].

Прямая задача состоит в расчете векторов декартовых координат r(q), линейных скоростей v(q, q) и ускорений w(q, q,q) заданных точек в кинематической цепи манипулятора, а также кватернионов либо матриц ориентации, векторов угловых скоростей и ускорений звеньев в СК манипулятора Omxmymzm при заданных значениях векторов координат q = {qs}, 5 = 1 ^ 6, скоростей q и ускорений q. Для решения прямой задачи кинематики использу- ется обратный рекуррентный переход из i -ой в (i — 1) -ую СК, начиная с последнего звена до стойки при i = 1 [7].

Обратная задача заключается в вычислении вектора угловых координат q = { q₅ } по заданным декартовым координатам вектора r _D = { x _D , y _D , z _D } точки D схвата и ориентации СК последнего звена манипулятора относительно этой же СК O _m x _m y _m z _m стойки (master) при ограничениях (6). В общем случае решение обратной задачи неоднозначно, но для схемы на рис. 2 гарантируется единственное решение при наличии возможности перемещения звена 3 с точкой D в отрицательном направлении оси O_m z _m, см. рис. 1.

Представленные в [2] законы наведения схвата манипулятора при переходах между целевыми состояниями с краевым условиям по каждой из угловых координат q_s учитывают два важных аспекта: (i) расчет значений времени начала t i (initial), завершения t _f (final) и длительности T _m = t _f — t i выполнения каждого этапа и (ii) формирование временных зависимостей углов q₅ ( t ) , скоростей q₅ ( t ) и ускорений q₅ ( t ) при ограничениях на углы (6), а также на модули скоростей и ускорений

I <7 5 ⁽ t ) 1 ^ q *, I q 5 ⁽ t ) ^ q V t E T m г [ t i , t f ] (8) при заданных значениях параметров q * и q* . Здесь каждый из последовательных этапов перемещения содержит стандартные участки разгона, движения с постоянной скоростью и торможения. При цифровом управлении редукторными электроприводами по степеням подвижности манипулятора применяются адаптивно-робастные алгоритмы с эталонной моделью наведения [8].

В [2] для простейшей оценки потребных моментных характеристик электромеханических приводов манипулятора вычисляются обобщенные силы – крутящие моменты на выходных валах приводов, когда их нагрузка представлена только обобщенными силами инерции при движении звеньев, а разнообразные моменты сил сопротивления такому движению не учитываются. В этом случае вектор обобщенных сил Q = Q ( t ) = { Q s ( t )} вычисляются по соотношению

Q ⁽ t ⁾ = ^{A (} q ⁽ t ⁾⁾ ii ⁽ t ^{) +} b ⁽ q ⁽ t ^), q ⁽ t ^)), (9)

где A ( q ) = A ( q ( t ) - симметричная матрица инерции и b ( q ( t ), q ( t )) - вектор центробежных и кориолиссовых сил, приведенных к выходным валам приводов в шарнирах манипулятора.

В статье решаются задачи синтеза законов цифрового робастного управления при замене оборудования с массой 300 кг и 400 кг, оценки потребных характеристик электромеханических приводов манипулятора и компьютерного анализа динамики СУД в указанных условиях.

АНАЛИЗ ДИНАМИКИ СИСТЕМЫ ПРИ ЗАМЕНЕ ОБОРУДОВАНИЯ

Анализ динамики СУД при замене оборудования выполнен на основе методов и средств компьютерной имитации для следующих значений инерционных параметров механической системы твердых тел:

т_г = 3100 кг; J ° = 10³ diag{5,3,4}KrM²;

m_t = 3500 кг; J , = 10³ diag{20,18,13}KrM²;

массы первых трёх звеньев манипулятора равны 50, 35 и 15 кг соответственно; масса 4-го звена составляет 300 кг либо 400 кг, а сцепка КРМ и ГСС со всеми заполненными топливными баками имеет массу m = 6800 кг. Как и в [2], было принято, что период цифрового управления СГК T_u = 4 с, каждый ГД имеет собственный КМ h_g = 30 Нмс и ограничение u^g = 1 рад/с по угловой скорости прецессии.

При смене топливных баков массой 90 кг манипулятор выполняет такие действия: 1) схват переводится из транспортного положения rD = {xD, yD,zD} = {0,0,0} сначала к контейнеру ГСС с пустым баком f, который затем перемещается в пустой контейнер a КРМ; 2) схват переходит к контейнеру b КРМ и далее перемещает полный бак b в контейнер f ГСС, см рис. 1. Декартовые координаты целевых точек рабочей зоны манипулятора в его СК Omxm ymzm и последовательность действий манипулятора во времени представлены в таблице 1 статьи [2]. Изменения угловых координат манипулятора при замене оборудования приведены на рис 4. Здесь в отличие от смены топливных баков отсутствует этап первого перемещения пустого бака, поэтому основные динамические процессы начинаются только с 195 секунды.

Робастность цифрового алгоритма управления СГК (6) достигается за счёт рекуррентного перерасчета значения тензора инерции (2) по явным аналитическим соотношениям с использованием измеренных значений угловых координат манипулятора с периодом дискретности, кратном периоду управления СГК. На рисунках 5 – 8 представлены результаты компьютерной имитации динамических процессов при замене оборудования массой 300 кг. Так, на рис. 5 приведены угловые отклонения связки КА относительно ОСК и её угловая скорость, на рис. 6. – управляющий момент СГК и скорости прецессии гиродинов, на рис. 7 – изменения смещения и поступательной скорости центра масс и на рис. 8 – оценки потребных моментов приводов манипулятора.

Угловые отклонения связки КА в ОСК и скорости прецессии гиродинов при замене оборудования массой 400 кг представлены на рис. 9. Нетрудно убедиться в наличии свойства робастности СУД космического робота при таком существенном изменении массы заменяемого оборудования.

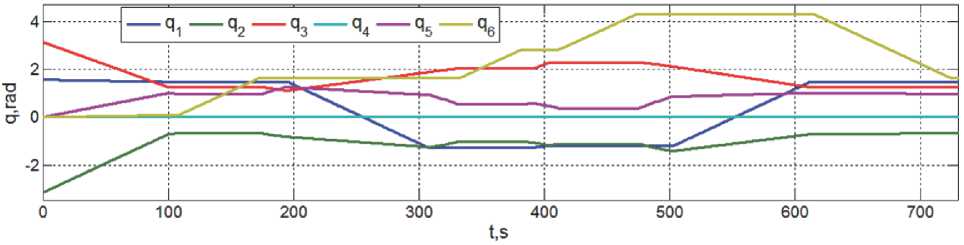
Рис. 4. Изменение угловых координат манипулятора при замене оборудования

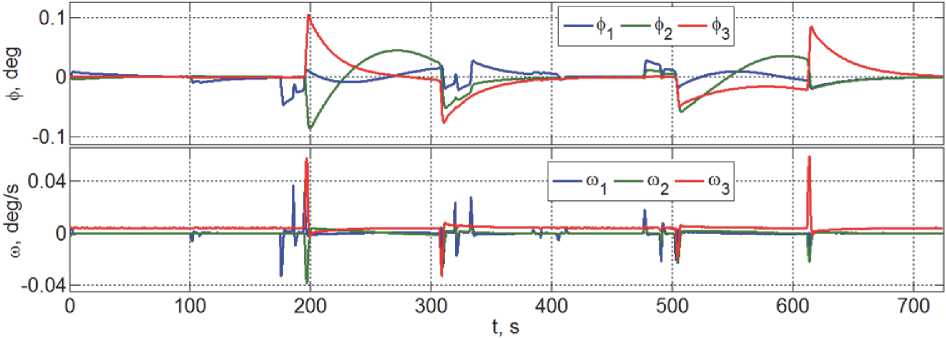
Рис. 5. Угловые отклонения и угловая скорость при замене оборудования массой 300 кг

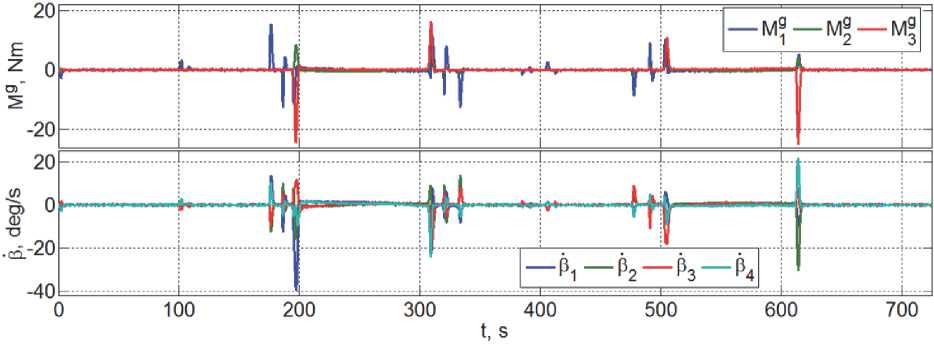
Рис. 6. Управляющий момент СГК и скорости ГД при замене оборудования массой 300 кг

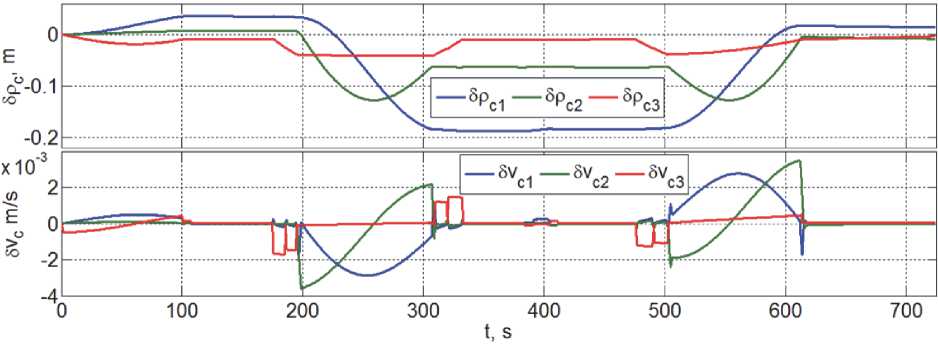
Рис. 7. Изменения смещения и скорости центра масс при замене оборудования массой 300 кг

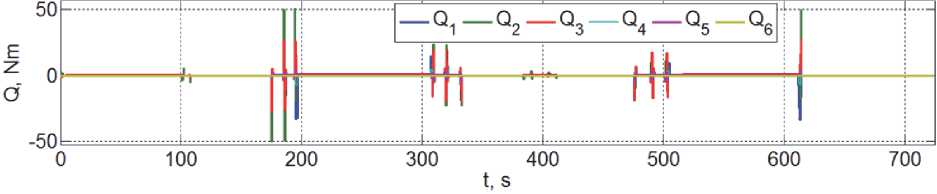
Рис. 8. Оценки потребных моментов приводов манипулятора при замене оборудования массой 300 кг

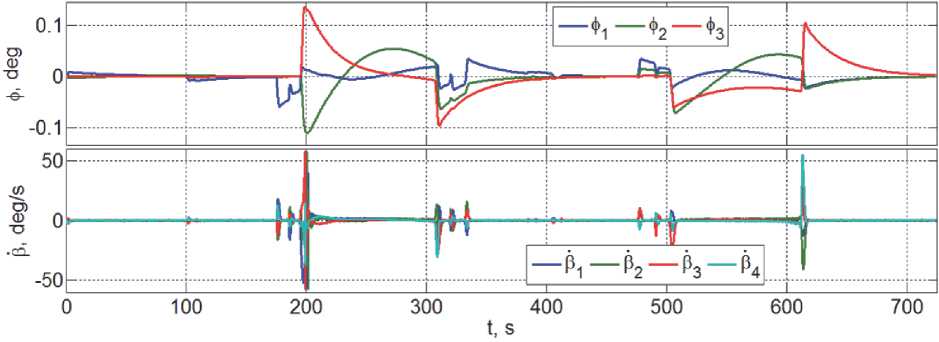
Рис. 9. Угловые отклонения связки КА в ОСК и скорости ГД при замене оборудования массой 400 кг

ЗАКЛЮЧЕНИЕ

Кратко представлены разработанные методы робастного управления космическим робо- ^2. том-манипулятором при полётном обслуживании геостационарного спутника связи – замене топливных баков, панелей солнечных батарей и других сменяемых компонентов системы 3. управления движением спутника, что приводит к значительным изменениям инерционных параметров жесткого сцепления робота с геостационарным спутником.

Для конкретных исходных данных уста- ₄ новлены требования к электромеханическим ^. приводам манипулятора и представлены результаты компьютерной имитации типовых динамических процессов при техническом обслуживании геостационарного спутника связи с 5. одновременной угловой стабилизацией связки робота и геостационарного спутника в орби- ^6. тальной системе координат.