Робастное управление при формировании вращающейся тросовой группировки микроспутников конфигурации «ступица-спицы» с использованием неравенства Гамильтона-Якоби

Тросовые группировки космических аппаратов (ТГКА) считаются одной из перспективных технологий, позволяющей обеспечить согласованный полет космических аппаратов (КА). По сравнению с традиционными космическими системами КА, несоединенными между собой механическими связями (тросами), ТГКА позволяют формировать на орбите надежную легкую структуру с большим разнообразием геометрических конфигураций. Конфигурации ТГКА могут поддерживаться на орбите долгое время, и при этом требуется низкий расход топлива благодаря тому, что силы натяжения тросов могут использоваться в качестве управляющих сил, что является ключевой особенностью космических тросовых систем (КТС) [1].

В последние годы большое количество исследований было сосредоточено на анализе динамики и разработке методов управления КТС, состоящей из двух КА и развернутой в положение, близкое к местной вертикали [2–4]. Когда речь идет о ТГКА, обычно имеются ввиду тросовые системы, состоящие из нескольких КА, причем в зависимости от требований космических миссий, входящие в такие системы КА образуют определенные геометрические конфигурации, например, «линия» [5], «кольцо» [6], «ступица-спи-

Том 6

цы» [7] и др. Доказано, что ТГКА может выполнить множество миссий, таких как космическая интерферометрия, многоточечные распределенные измерения на орбите, исследование дальнего космоса и др.

Среди перечисленных выше конфигураций ТГКА, система «ступица-спицы» привлекла особый интерес исследований. В такой системе центральный КА играет роль «ступицы», а спутники, находящиеся на периферии, соединяются с центральном телом тросами («спицами»). Движение ТГКА в виде «ступица-спицы» имеет свою осо- ²³⁶ бенность, которая заключается в том, что для обеспечения устойчивости системы она должна вращаться вокруг центра масс с некоторой угловой скоростью [8]. Формирование вращающейся ТГКА конфигурации «ступица-спицы» является сложной задачей. Чаще всего в настоящее время во многих работах центральный КА рассматривается как материальная точка. Однако чтобы учесть сложное взаимодействие центрального КА и тросов в процессе формирования системы, необходимо учитывать размеры центрального КА [9]. При этом важным является учет действующих возмущений. В связи с этим актуальной является задача разработки робастного управления на этапе формирования ТГКА.

Настоящая работа посвящена задаче управления при формировании ТГКА конфигурации «ступица-спицы», вращающейся в орбитальной плоскости. В состав рассматриваемой системы входят центральный КА и несколько микроспутников. Предполагается, что в исходном состоянии микроспутники жестко соединяются с центральным КА и повторяют конфигурацию «ступица-спицы», которая вращается вокруг центра масс системы с некоторой начальной угловой скоростью. Конечная конфигурация ТГКА – это также конфигурация «ступица-спицы», вращающаяся с угловой скоростью, равной начальной. При анализе динамики системы центральный КА рассматривается как твердое тело, а микроспутники – как материальные точки. Тросы – неупругие невесомые нерастяжимые механические связи переменной длины. Угловая скорость вращения КА поддерживается постоянной с помощью управляющего вращательного момента. Для разработки закона выпуска тросов используется скользящий режим управления. Определяется показатель робастности системы при наличии периодических гравитационных возмущений, вызванных вращением КА, и других внешних возмущений. Устойчивость движения системы анализируется с помощью теории Ляпунова и неравенства Гамильтона-Якоби. Приводятся результаты численного моделирования, иллюстрирующие эффективность предлагаемой схемы управления при действии различных типов возмущений.

1.    Математическая модель движения ТГКА конфигурации «ступица-спицы»

В схему рассматриваемой ТГКА, представленной на рис. 1, входят центральный КА массой m_c и n микроспутников массой m_i , i = 1, 2, …, n . Здесь КА рассматривается как симметричный однородный цилиндр радиусом r_c и длиной h_c . Тросы – невесомые нерастяжимые механические связи длиной l_i , i = 1, 2, …, n . Кроме того, при описании движения ТГКА принимаются еще следующие допущения:

• 1)    Система движется по неизменной круговой орбите.

• 2)    Выпуск тросов происходит в плоскости орбиты.

При построении математической модели используются геоцентрическая система координат OXYZ и орбитальная подвижная система координат Cxyz (рис. 1). Начало O находится в центре масс Земли, плоскость OXY совпадает с плоскостью экватора и ось OX направлена от O в точку весеннего равноденствия, ось OZ направлена по оси вращения Земли. Орбитальная система координат Cxyz связана с центром масс КА, причем предполагается, что в процессе развертывания конфигурация системы близка к симметричной, что обеспечивается системой управления. Поэтому полагается, что центры масс КА и системы совпадают. Тогда ось Cx направлена по радиус-вектору R _c центра масс КА, а ось Cy расположена в плоскости орбиты и ориентирована по направлению движения системы. Орты системы координат Cxyz задаются как i _c , j _c , k _c . Система движется по круговой орбите с угловой скоростью Ω = Ω k _c .

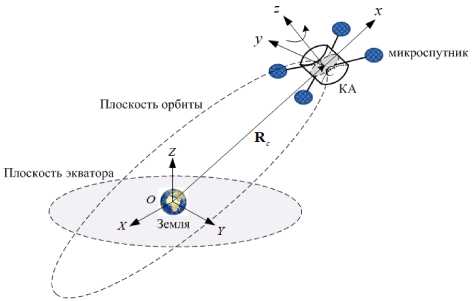
Рис. 1. Схема ТГКА и используемые системы координат

Для вывода уравнений движения ТГКА используются уравнения Лагранжа:

d (аTk) аTk_ ап 1 I—+ Q

dt ^ dq )  dq    dq

где T_k и П – кинетическая и потенциальная энергии системы; q , q – векторы обобщенных координат и скоростей; Q – вектор обобщенных сил.

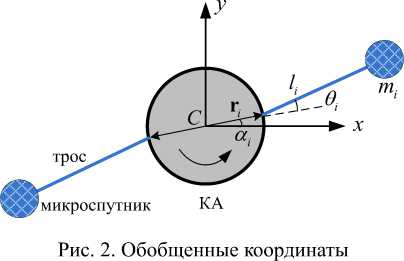
Для описания вращательного движения центрального КА относительно своего центра масс используются углы α _i (рис. 2). На рис. 2 векторы r _i ( i = 1, 2, …, n ) определяют положения точек крепления тросов, причем при их симметричном расположении имеем | r i | = r c . Развертывание i -го троса характеризуется длиной l_i и углом θ _i , который определяет отклонение i -го троса от направления вектора r _i (рис. 2). Таким образом, положение i -го микроспутника в орбитальной системе координат может быть выражено как:

Р г = V i c + Уг * ^j c + zi • ^k c , i = U,-, n , ⁽²⁾

4>i( li + irc cos ei) ei— ymr sinQl + i=1

n

+Zmi[2li(ai - ei +Q)(li+ rc cosei )— i =1

• - r c l i e_t( 2a i - e ■ 2 Q ) sine _; ] + d „ = Q a_ ,

  ^{) +}

  
  

(I

• e, - 1 + rc -cosO, a -2^ a,. - 9,. +q z                      7                  г г 1 \ I I

V li           J

+ rc sin Oja,2 + 2Qa ) + d„ = li        1( ‘           i) ei    mil2

где:

xf = rc cos az. +1 cos ( a - 0z), y. = r sin a. +l sin(a, - 0.), z. = 0.

i    c      ii       i    i     i

Поскольку тросы считаются невесомыми, то

кинетическая энергия системы, входящая в уравнение (1), определяется следующим образом:

T = ¹

J c ( Q + a i ) ² + m v ² +

V r c ^sin 6(^a i ^{- l} i ( ^a i ^- 9 1 ⁺ ^ ) ² -^ ^{2 -}

_Q           (7)

-rc cos 9i (ai2 + 2Qai) + dl = —1l , i    mi где Q α , Q θ , Q l – обобщенные силы, d α , d θ , d l – периодические члены гравитационных возмущений,

n

+ E m i ( v c ⁺ v i M v c ⁺ v i )

i = 1

i = 1,2,..., n,

где J_c – момент инерции центрального КА, v _c = fi x R c — вектор орбитальной скорости центра масс системы, v i = p i + Q x p i - вектор скорости i -го микроспутника относительно КА.

вызванные вращением системы и имеющие следующий вид:

d _a = d 0 IL m i [ 0,5 r c2 sin 2a i + i = 1                                          (8)

+ 0,5 l i ² sin ( 2a i - 29 i ) + r c^ sin ( 2a i - 9 i ) ] ,

d _B i =- d о [ cos ( ^a i - e , .) sin ( a - 9 i ) + + r _c cos a i sin ( a i - 9 i )/ l i ] , d^ = - d ₀ [ l i cos ² ( a i - 9 i ) + + r c cos a i cos ( a i - 9 i ) ] , где d ₀ = 3Q².

2. Программа управления при формировании конфигурации «ступица-спицы»

Поскольку тросы считаются нерастяжимыми, то общая потенциальная энергия, обусловленная гравитацией, определяется как:

П = - ц

m_cⁿ     m_i

I R e l   M |R c + P i|

, i = 1,2,..., n ,    (4)

где μ – гравитационная постоянная.

Подставляя (3) и (4) в уравнения Лагранжа и рассматривая α _i , θ _i , l_i как обобщенные координаты, получим уравнения движения ТГКА в подвижной системе координат, которые записываются в следующем виде:

n

J_c + ^ mi ( ^r _c ² + l i + 2 l i r_c cos9 i ) a i i = 1                                                _

—

Основная цель при формировании рассматриваемой ТГКА состоит в том, чтобы разработать схему управления для перевода системы в конечное заданное состояние при сохранении желаемой конфигурации. Для этого, во-первых, необходимо стабилизировать вращательное движение центрального КА; во-вторых, в процессе развертывания тросов необходимо исключить их касание друг с другом и с корпусом центрального КА. Поэтому в конечный момент движение системы должно удовлетворить следующим условиям: a i ( t_f ) = 0, a i ( t f. j = a i ( 1 ₀ ) = ш_а = const, 0 i ( t f ) = 0, 10 i ( t f )| = 9 _d = const < п/2, ^ t , ) = ^ C t, ) = 0, ^l i ( t , ) = L .

Том 6

Здесь ω_α – заданная скорость вращения системы; θ _d , l_d – конечные значения угла наклона и длины тросов соответственно.

При выпуске тросов необходимо чтобы угловая скорость вращения КА была постоянной и равной ее начальной угловой скорости. Это можно обеспечить с помощью управляющего момента τc, действующего на центральный КА. Таким образом, обобщенная сила Q = τ . А при определении обобщенных сил Q θ и Q l учитываются реактивные силы малой тяги Fi (ортогональны тросам), приложенные к микроспутникам, и силы натяжения T. Тогда Q^ = -Fl, Q^ = -T.

Исходя из поставленной цели управления, предлагается схема системы управления движением ТГКА конфигурации «ступица-спицы» (рис. 3). Приведенная схема основана на предположении, что во время выпуска тросов вращение КА известно (угловая скорость постоянна), что обеспечивается действием момента τ _c . При этом основное внимание сосредоточено на разработке робастного управления процессом выпуска тросов.

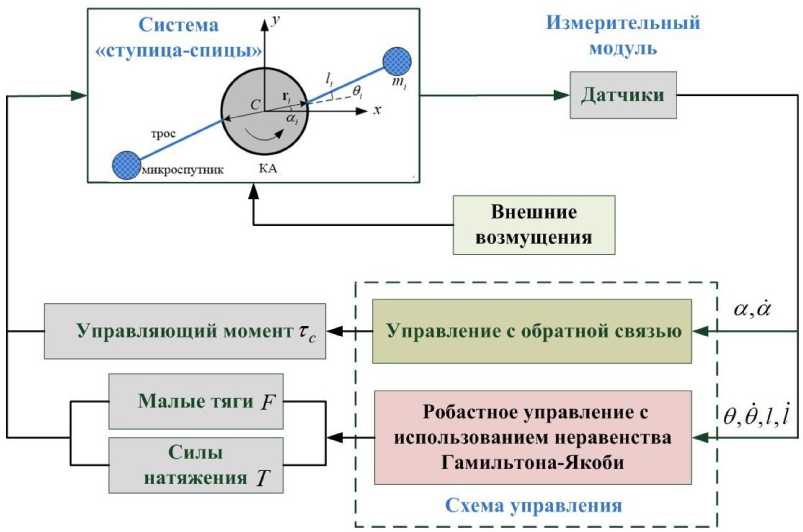
Рис. 3. Структура схемы управления

Управляющий момент τ _c задается с использованием принципа обратной связи [10]:

Tc = rckm ( a - ®a ) + ka ( a - ®a ‘ t ),      (11)

где k _ω и k _α – коэффициенты обратной связи по скорости и углу вращения КА, co_a = a i ( Z_o ) - начальная скорость вращения КА. Здесь стоит отметить, что уравнение (5) для α _i имеет одинаковый вид, поэтому в (11) для краткости был опущен низкий индекс i .

При допущении, что:

α ≈ω =const, α ≈0, уравнения (6) и (7), описывающие развертывание тросов, принимают вид:

Далее при разработке закона управления развертыванием тросов используются упрощенные уравнения (12) и (13), а для проверки эффективности предлагаемой схемы управления применяется полная модель, т. е. система уравнений (5)–(7). В уравнениях (12) и (13) индекс i также может быть опущен, так как эти уравнения одинаковы для всех тросов. Введем вектор состояний системы:

x = [ xx x2 ]T =[9 l ]T.

Уравнения (12) и (13) переписываются в виде:

x + V ( x , x ) x + G ( x ) + d ( x ) = M ( x ) U ,   (14)

0i— 21.( ®a

—

где:

+ r c sin ⁰ i ( ® 2 + 2Q® a ) ,^l i + d 0 ,

(12) = — Fjmili .

V ( x , x )=

-1 (6 - 2roa - 2Q)

-2 ( ... +П)/l

,

li - l (

®a - 9 i +q)2 -q 2

-

-rc cos 9i (®2 + 2Q®a) + d,t = -T /mi .

G ( x ) =

r c ^{sin 9} ( ® a ^{+ 2Q} “ a ) I¹

-(l + rc cos 9)(Ю2 + 2Q®„)_,

d ( x ) = [ d^ + A₀ d l + A _z ]^T - вектор суммы периодических гравитационных возмущений и внешних возмущений, M ( x ) = diag ( - 1/ ml , -1/m ) ,

U = [ F T ] - вектор управляющих сил.

Пусть вектор конечных состояний системы x d = [ X d ^x 2 d ]^T = [ ⁹ d l^T Г ^и вектор отклонений от него e = x - x _d = [ e_x e ₂ ] . Предлагается следующий закон управления:

U = M ( x ) ^{- 1} [ A u + x _d + V ( x , x ) x _d + G ( x ) ] , (15) где ∆ u – управление, которое определяется ниже. С учетом того, что x _d = x _d = 0, форма управления U упрощается:

U = M ( x ) ^{- 1} [ A u + G ( x ) ] .

Подставляя закон (15) в (14), получим:

e + V ( x , x ) e + d ( x ) = A u .         (16)

Далее для (16) используется более короткое обозначение e + Ve + d = A u . Поверхность скольжения задается следующим образом:

s = e + ce ,                  (17)

где c = diag ( c ₁, c ₂) – матрица коэффициентов, и здесь c ₁, c ₂ – положительные действительные числа.

Поверхность скольжения (17) может быть переписана как e = s - ce . Дифференцируя (17), получим:

s = e+ce .

Подставляя (16) и (17) в (18), найдем:

s = e+ce = - v e - d +A u+ce =

= - V ( s - ce ) - d + A u + ce =

= - Vs + ( Vce + ce ) - d + A u =

= - Vs + W - d + A u ,

где W = Vce + ce .

Далее пусть y = [ e s ] , тогда система уравнений (17) и (19) переписывается в виде:

_< ^y = f ( y ) ⁺ g ( y ) ^d _ z = h ( y )

где:

оценки, например, функция ошибки. Для робастности системы определяется следующий показатель, характеризующий устойчивость и нечувствительность системы к возмущениям:

J = sup

II d| L ₂ * 0

II z| L IId| L ^,

где 11 z 11 _L = t d J z ^T z dt , 11 d 11 _L = J d ^T d dt - нормы век-² У 0 ² У 0

торов z , d на пространстве L ₂ (Гильбертово пространство), «sup» обозначает точную верхнюю границу. Здесь показатель J также называется L ₂-усиление ( L ₂-gain) [11]. Очевидно, что при низком показателе J система (20) обладает свойством высокой надежности, и это может быть достигнуто путем разработки подходящего управления ∆ u . Для этого используется теорема о неравенстве Гамильтона-Якоби (HJI – Hamilton-Jacobi Inequality), которая изложена ниже.

Теорема . Пусть γ > 0 – некоторая положительная константа, тогда для системы (20) если существует положительно определенная дифференцируемая функция L ( y ), которая удовлетворяет неравенству:

^{L (} y ) = ^ ^y ~ [ f ⁽ y ^{) +} g ( y ) ^d ]^ ^yy           (22)

^ 2 {Y21d Г-Iz 2}, Vd, то индексный показатель робастности системы (20) J ≤ γ [11].

Для того чтобы показатель робастности разработанного контроллера удовлетворял J ≤ γ, управление ∆ u для системы (20) зададим:

A u = Vs - W s - d ⁰-s .       (23)

2 y ²      2

Анализ устойчивости системы и доказательство робастности с управлением (23) заключаются в следующем. В качестве функции Ляпунова принимается следующая положительно определенная функция:

- Vs + W + A u

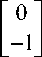
z = d ₀ s .

1L = sTs, 2

производная которой имеет вид:

Чтобы найти робастное управление, сначала необходимо определить, как оценить робастность системы. Для этого можно использовать следующее определение [11].

Определение . Дана нелинейная система с несколькими входами и выходами, например (20), где y e9t ^{n x 1} , f( y ), g ( y ) - непрерывные функции, d – вектор возмущений, z – введенная функция

L = s ^T s = s ^T ( - Vs + W - d + A u ) =

= s ^T

V

d ¹ .   ^{d 12}.1

^{- d -} 27 s - т ^s ) .

Пусть

H = L - 2 Y 21 |d| f + 2 | z | Г,

Подставляя (25) в (26), получим:

H = — s T d — 1r s ^T s 2γ ²

—

d ²

0 s T s

—

V

— s ^T d — 1y s ^T s

2γ ²

—

—

1 _γ 2 d

- s + Y d

γ

—s + Y d ^γ

1Y ‘I Id Г +1H Г =

—fsT s+1И =

— f s^T s + 1| d » s| Г =

1 ₂       2

Из H ≤ 0 следует, что L ≤ γ ² d

- 12 z ² . Та-

ким образом, система (20) асимптотически устойчива. Более того, согласно Теореме система (20) обладает робастностью, показатель которой мень-

ше γ.

3. Результаты численного моделирования и их анализ

Проводится численное моделирование движения ТГКА с применением управляющего момента (11) и закона управления (15). В качестве примера при моделировании рассматривается система «ступица-спицы», в которую входят два микроспутника i = 1, 2. Были приняты следующие массово-геометрические параметры системы: масса КА m_c = 500 кг, его радиус r_c = 1 м, длина h_c = 1 м, момент инерции J _c = 0,5 m _c r_c ² , масса микроспутников m ₁ = 10 кг, m ₂ = 12 кг. Высота орбиты H_c = 500 км и начальные условия движения системы:

a1 (0) = 0, a2 (0) = n, ai (0) = 50Q,

11(0) = 0,5м, 12(0) = 1м, li(0) = 0,5м/с,

9г (0) = 0,1рад, 9г (0) = 0.

Характеристики состояния системы в конечный момент времени:

ai (tf.) = 50Q, li (tf.) = 1d = 100 м, li (tf)=0, e,( tf)=9i( tf)=0.

Коэффициенты программы управления приводятся в таблице.

Таблица

Значения коэффициентов программы управления

Описание	Значение
Коэффициенты обратной связи k ω, k α	100; 0,01
Матрица коэффициентов поверхности скольжения c = diag ( c 1, c 2)	c = diag (0,02, 0,02)
Параметр γ	1

Том 6

На ТГКА, которая движется на низкой околоземной орбите, действуют следующие основные возмущения: гравитационный момент, аэродинамические силы, давление солнечного излучения. Суммарная величина этих возмущений не превышает 1∙10-5 [12]. Для того чтобы продемонстрировать способность подавления указанных возмущений предлагаемой схемой управления при моделировании используется комбинация гармонических составляющих, частоты которых характеризуются как низкими, так и высокими составляющими, причем низкая частота соответствует периоду орбитального движения системы, а высокая частота – периоду вращения системы вокруг центра масс. Таким образом, имеем:

A = 1-10-4 [sin (Qt) + sin (wa t)], где амплитуда возмущений превышает известные оценки.

На рис. 4–6 проводятся зависимости, характеризующие изменения от времени переменных состояний системы «ступица-спицы». Из рис. 4 следует, что процесс вращательного движения центрального КА характеризуется почти постоянной заданной угловой скоростью:

ша = 50Q« 0,0554 рад/с.

На начальном этапе угловая скорость вращения немного уменьшается из-за увеличения момента инерции всей системы в целом. При завершении процесса развертывания системы угловая скорость α стремится к заданному значению ω_α, и, как показано на увеличенном фрагменте на рис. 4, значение α изменяется с периодом, близким к периоду члена гравитационных возмущений d _α, соответствующему формуле (8):

T_{d α} ≈ πω_α.

Помимо колебаний, вызванных вращением КА, наблюдаются также и колебания с более высокой частотой из-за взаимодействия движений КА и тросов.

Из рис. 5 следует, что углы θ₁ и θ₂ уменьшаются от начального значения до нуля. В этом процессе также имеет место влияние гравитационного возмущения d _θ, которое колеблется с тем же периодом, что и d _α. Изменение длин l ₁ и l ₂ и скорости выпуска тросов от времени приводится на рис. 6. Как следует из результатов, длины первого и второго троса приближаются к заданному конечному значению (0,1 км) по завершении развертывания, хотя их начальные длины отличаются.

На рис. 7 показано как изменяется управляющий момент от времени. Из-за того, что массы двух микроспутников не равны, максимальные значения тяги и конечные значения силы натяжения отличаются, что следует из рис. 8.

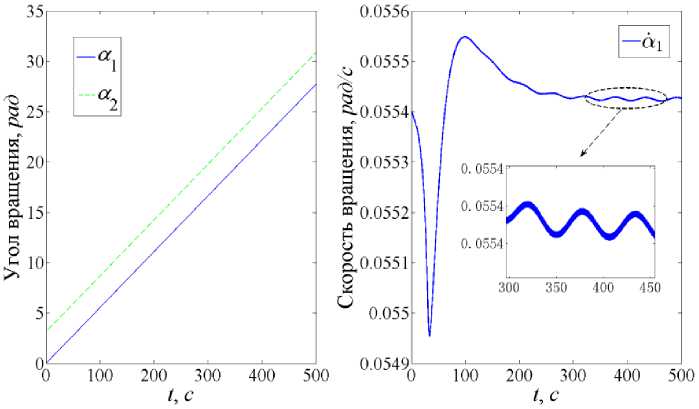
Рис. 4. Изменение угла и угловой скорости вращения системы

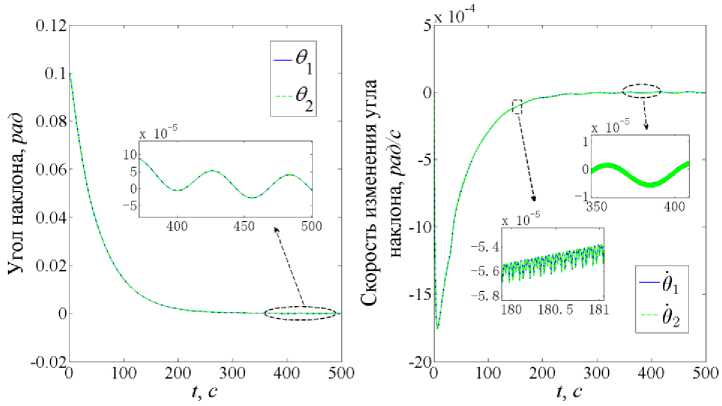
Рис. 5. Изменение угла и угловой скорости вращения троса

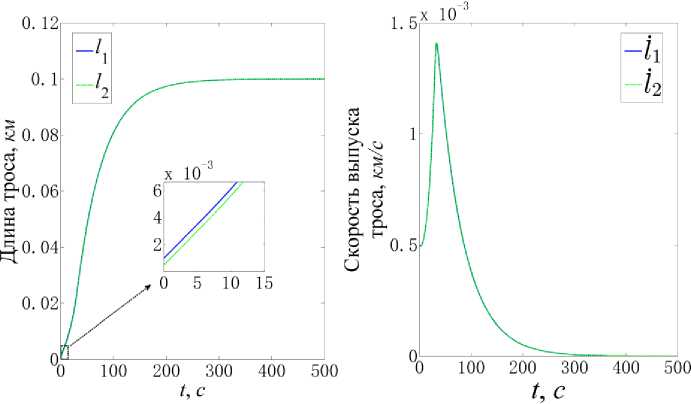
Рис. 6. Изменение длины и скорости выпуска троса

Том 6

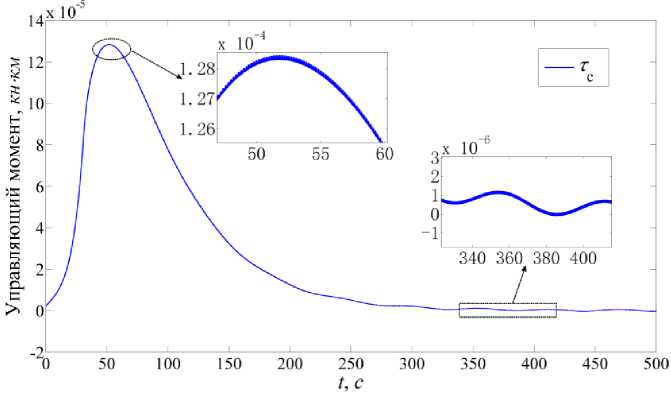
Рис. 7. Изменение управляющего момента τ _c

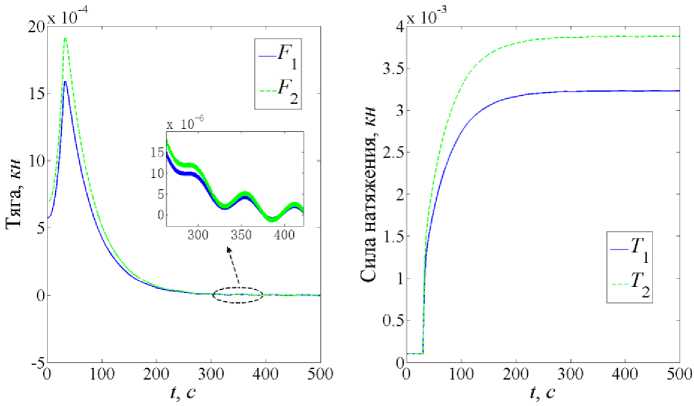
Рис. 8. Изменение управляющих сил

Рис. 9 иллюстрирует изменение показателя робастности системы. В процессе развертывания ТГКА выполняется условие J < γ = 1. На рис. 10 приводятся изменения компонент поверхности скольжения s от времени, откуда следует, что значения всех компонентов приближаются к нулю, подтверждая асимптотическую устойчивость движения при использовании предлагаемого управления.

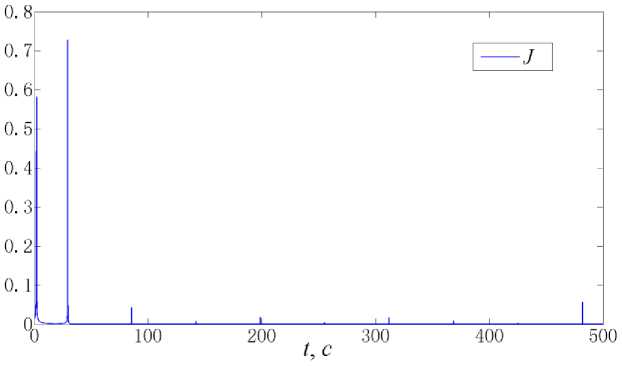
Рис. 9. Изменение показателя робастности J

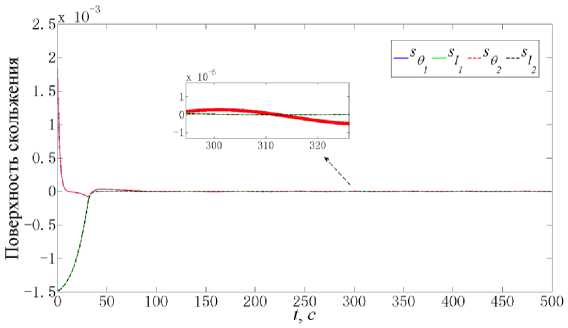
Рис. 10. Изменение компонент поверхности скольжения

Заключение

В данной работе рассматривалось управление движением ТГКА конфигурации «ступица-спицы», вращающейся в орбитальной плоскости. При построении математической модели центральный КА рассматривался как однородный цилиндр, микроспутники – как материальные точки. Предложена комбинированная схема управления при развертывании системы, включающая в себя стабилизацию вращения КА, создание вращательных моментов с помощью двигателей, расположенных на КА, и предложенный закон робастного управления для безопасноговыпускатросов. Причисленноммодели-ровании учитывались влияния внешних возмущений и возмущений, связанных с начальным состоя- нием системы. Результаты моделирования подтвердили эффективность предлагаемой схемы управления и возможность ее использования для формирования ТГКА в виде вращающейся системы «ступица-спицы» при действии возмущений. В качестве развития работы далее планируется проанализировать угловое движение микроспутников и его влияние на процесс формирования системы «ступица-спицы».

Работа выполнена при финансовой поддержке Государственного фонда естественных наук Китая (проект № 62111530051) и РФФИ (проект № 21-51-53002).