Робастные непараметрические оценки линейных функционалов

Пусть у ₁, ..., y_M – выборка непараметрической оценки регрессии (НОР) с функцией распределения (ФР) G ( y ) и 0 = j ф ( Г ) dH ( Г ) < да , где t = ( t 1 , ..., t m ) T ; H ( t ) = G ( t 1 ) ■■■ G ( t m ). Непараметрические оценки функционала 0 при симметричных функциях ф ( t ) получили название U -статистик [1; 2]. В классе робастных оценок 0 применяется метод усечения выборки – усеченные U -статистики [3].

Обозначим через f ( x ) и F ( x ) плотность и ФР случайной величины X = ф ( Y 1 ,..., Y m ), тогда 0 = | zdF ( z ). Выборку Y ,..., Y m преобразуем в выборку x 1 ,..., x_N , где x j =ф ( y i .,..., y ^); N - мощность множества { i 1 <  i ₂ < ... <  i m } . При таком преобразовании задача оценивания параметра 0 сводится к задаче оценивания параметра сдвига распределения F ( x ). В параметрической статистике такой прием широко используется для синтеза несмещенных оценок параметров как функций от достаточных статистик и в вычислительном отношении достаточно удобен, однако основная сложность здесь связана с переходом от распределения G ( y ) к распределению F ( x ) [4]. В связи с этим будем считать, что вид ФР F ( x ) нам неизвестен и задача относится к классу непараметрических задач оценки параметра сдвига.

В настоящее время нет недостатка в робастных оценках параметра сдвига, что создает даже определенное неудобство для пользователей (см. например, [3; 5] и библиографические списки к ним). Отметим ряд особенностей таких оценок. Большинство из них робастны на классе и имеют низкую эффективность в отсутствии выбросов. Как выход предложены адаптивные оценки: в основном используется адаптация по параметру усечения, но не по виду F ( x ) [3], или адаптация ведется по виду распределения F ( x ), но функция и параметр усечения подбираются эвристически [ 6 ] . Эта работа Р. Берана интересна в двух аспектах: в ней, очевидно, впервые введены робастные непараметрические оценки плотности, а также использован метод подстановки на основе этих оценок для получения оценки параметра. Становится понятным, что робастные эффективные оценки должны быть адаптивными как по виду основного распределения, так и по отбраковке выбросов.

В данной статье на основе взвешенного метода максимального правдоподобия (ВММП) [7; 8] синтезированы адаптивные робастные непараметрические оценки и показано их использование для оценки линейных функционалов.

Взвешенный метод максимального правдоподобия. Пусть F ( x , 0 ) - унимодальное непрерывное распределение с плотностью f ( x , 0 ) и неизвестным параметром 0 - принадлежит к классу унимодальных распределений и x ₁ , ..., x_N – выборка НОР из распределения F ( x , 0 ). Обозначим через F N ( x ) эмпирическую функцию распределения (ЭФР), а через g ( x , 0 ) -априорную плотность распределения.

М -оценки неизвестного параметра 0 можно определить на основе решения эмпирического уравнения вида

/ ф ( x , 0 N ) dF N ( x ) = 0, (1)

где ф ( x , 0 ) - оценочная функция.

Анализ критерия радикальности и алгоритмов устойчивых оценок [5] позволяет сделать вывод, что все эти оценки можно получить на основе ВММП с оценочной функцией ф ( x , 0 ) вида

ф ( x , 0 ) =

д

— In g ^{( x} , ^{0 )} + Р g ^{( x} , ^{0 )}, д0

где I - параметр радикальности оценки; в - параметр, который определяется по условию несмещенности оценки, в нашем случае в = 0 [7].

Нетрудно заметить, что (2) определяет ВММП с весами g¹ ( x , 0 ). При I = 0 мы получаем оценки максимального правдоподобия (ОМП), при I = 0,5 - радикальные оценки, при I = 1 - оценки максимальной устойчивости (ОМУ) [5]. Физически роль параметра l вполне понятна и сводится к определению степени мягкого усечения как для удаленных выбросов, так и по форме априорного распределения. Таким образом, варьируя параметром l , можно получать эффективные оценки при локальных отклонениях распределения F ( x , 0 ) от априорного в классе устойчивых оценок.

В непараметрическом случае, когда вид g ( x , 0 ) неизвестен, заменим g ( x , 0 ) в (2) непараметрической симметризованной оценкой Розенблатта–Парзена

Г 29 — х — t I gN (x, 0) = — f KI 0 x t I dFN (t).       (3)

N V N )

Например, для нормального ядра уравнения для оценки параметров сдвига 0 и масштаба X принимают следующий вид [7; 8]:

N ( N - 1)

NN

ЕЕ (0 n

i = 1 * j = 1

- z j ) ■ W 1 ( z j ) = 0,

Выражение (5) определяет дисперсию параметрического ВММП (классические М -оценки) и при l = 0 (5) совпадает с выражением для дисперсии ОМП, а при l = 1 – с выражением для дисперсии ОМУ [7].

Для непараметрического ВММП

ф ( x , 0 , T 1 , T 2 ) = T 1 (x , 0 ) ■ T 2 ^{1 - 1} ( x , 0 ),

где

1 N N ( g _ ₇ A 1 ---¹— у у I ⁰ N z ij I - j- N ( N - 1) ^ЕЕ V X N ^J 1 + 1

^{W (} z j ) = exp

—

( 0 N - Z j ) 2

x N

X

N - 1

N

Е exp i * m =1

■ W 1 ( z j ) = 0,

Jx

( 0 N - Z m ) 2 Г

X N    J

xi + xj zj = —---полусуммы Уолша.

Рассмотрим обобщенную М -оценку 0 _N параметра 0 , которая определяется на основе решения эмпирического уравнения вида

J v ( x , 0 n , T n ( x , 0 n ) dF N ( x ) = 0,

1   Г 20 - x -11

S1(x, t, 0) =     K\-------------I, hN   V   hN   )

d

S 2 ( x , t , 0 ) = —S 1 ( x , t , 0 ).

d0

Выражение (5) определяет дисперсию непараметрического ВММП в зависимости от l.

Зависимости дисперсии параметрической (рис. 1) и вариации непараметрической (типа «складного ножа» jackknife) (рис. 2) оценок ВММП для модели Тьюки с асимметричным засорением от параметра радикальности 1 (0 <  1 <  1) приведены ниже (кривая 1 на рис. 1 – без выбросов, кривая 2 – 3 % выбросов, среднее – 4, кривая 3 – 10 % выбросов, среднее – 4; кривая 1 – на рис. 2 – без выбросов, кривая 2 – выброс – 5, кривая 3 – выброс – 11, N = 39 + 1 выброс).

где          T = ( T ,..., T k ) ^T ;          T i = J S ( x , t , 0 ) dF ( t );

T N = J S i ( x , t , 0 ) dF N ( t ).

В связи с ограниченностью объема статьи приведем без доказательства ряд результатов в окончательном виде.

Имеет место следующее представление:

—I-1

0 N -

^{- 1}

0= J—ф ( x , 0 , T ) dF ( x )    - J_V ( t , 0 ) dF ( t ),

d0

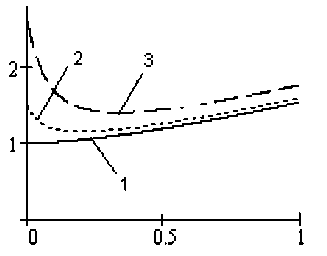
Рис. 1

V ( t , 0 ) = ф ( t , 0 , T ( t , 0 )) +

+Е [ S i ( x , t , 0 )^Ф( t , 0 , T(t , 0 )) dF ( x ).

i = 1                  d T i

При выполнении ряда ограничений NN ( 0 _N - 0 ) имеет асимптотически нормальное распределение с дисперсией

1 -2

G ²

- 2

= f —Ф ( x , 0 , T ^;) dF ( x )    Av ² ( t , 0 ) dF ( t ).

j d0                      J

Техника доказательства основана на работах Г. М. Кошкина ([9]) и результаты имеют место для стационарных процессов со слабой зависимостью.

В параметрическом случае ( S i = 0)

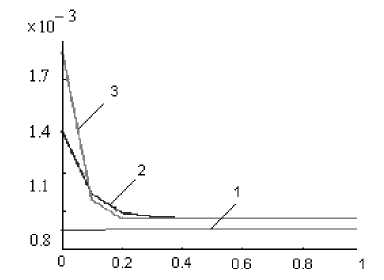
Рис. 2

ф ( x , 0 ) =

d

g ^{( x} , ^{0 )} d0

g‘ - ¹ ( x , 0 ).

Анализ дисперсии и вариации в зависимости от l (рис. 1, 2) показывает, что существует оптимальное l , доставляющее минимум дисперсии и вариации оценки.

Адаптивные оценки взвешенного метода максимального правдоподобного. Непараметрический подход на основе оценок Розенблатта–Парзена вида (3) позволяет осуществить адаптацию оценок ВММП по виду распределения. Адаптации по параметру радикальности l (0 ≤ l ≤ 1) производится с помощью бутстреп-метода. Для этого достаточно использовать простые бутстреп-процедуры типа «складного ножа» (jackknife) и алгоритмы поиска минимума вариации непараметрического ВММП. Моделирование также показывает, что при оптимальном l наблюдается и минимальное смещение оценки.

Примеры. Как отмечалось выше, значительный интерес представляет нахождение робастных непараметрических оценок для U -статистик. Применим для этого адаптивные оценки ВММП.

В первую очередь нас интересуют робастные непараметрические оценки функции распределения G ( t ) = ∫ C ( t - y ) dG ( y ) и плотности в виде g ( t ) = ∫ K (( t - y ) ⋅ h_N ^{- 1} ) dG ( y ), где С ( у ) – функция Хевисайда; K ( y ) – ядерная функция. Зафиксируем значение t = t ₀. От выборки у ₁, ..., y_M перейдем к выборкам x_i = C ( t ₀ - y_i ) для ФР и x_i = K (( t ₀ - y_i ) ⋅ h_N ^{- 1} ) для плотности соответственно.

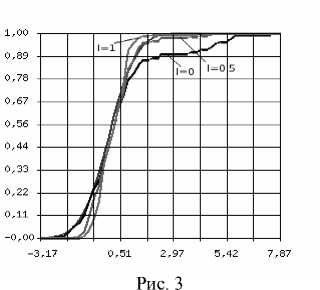
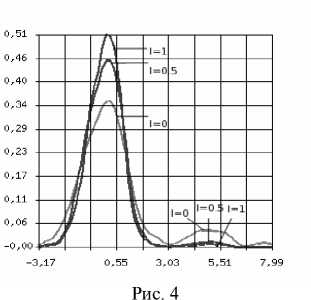
Представим результаты моделирования в зависимости от l для асимметричной модели выбросов Тью-ки ( N = 100, 10 % выбросов из нормального распределения со средним, равным пяти, рис. 3, 4). Хорошие результаты показывают радикальные оценки ( l = 0,5), l оптимально при l = 0,35, при l = 1 происходит достаточно сильное подрезание.

Результаты моделирования для вариаций оценок дисперсии ( x_k = 0,5 ⋅ ( y_i - y_j )) и средней разницы Джини ( x_k = y_i - y_j ) приведены на рис. 5, 6 ( N = 30 + + 1 выброс).

Таким образом, предложен адаптивный робастный непараметрический алгоритм нахождения линейных функционалов, который позволяет адаптивно (путем мягкого усечения) настраивать оценку в зависимости от исходного распределения и выбросов. Рассмотрено робастное оценивание функции распределения, плотности распределения типа Розенблатта– Парзена, дисперсии, средней разницы Джини. Проведено моделирование оценок для асимметричной модели засорений Тьюки. На модели эксперимента Бе-рана [7] проведено сравнение оценки Берана и вышеприведенной оценки. Они показывают одинаковые результаты, но в оценке Берана функция усечения и окно для нее (адаптация) подбирались эвристически [6]. Необходимо отметить, что представленный в данной статье подход позволяет применять робастные оценки ФР и плотности методом подстановки для получения адаптивных оценок неявных параметров от нелинейных функционалов.