Робастные самонастраивающиеся линейные и нелинейные системы управления динамическими объектами с сигнальной адаптацией

ми системы и могут быть определены аналитически или методом компьютерного моделирования по ее математическому описанию [2]. Однако возможность их уменьшения с использованием известных методов оказывается ограниченной (условиями устойчивости и местом приложения возмущающих воздействий в астатических системах). Ниже предлагается и исследуется новый закон управления [3], обеспечивающий улучшение динамических свойств систем стабилизации и полную инвариантность статической ошибки при задающих и возмущающих воздействиях в статическом режиме без интегрирующих элементов в основном контуре системы.

Решение осуществляется введением в замкнутую систему дополнительной (параллельно единичной) положительной обратной связи:

t

U ос = k 1 - J (x0 — x(t))dt , где x(t) – текущее значение регулируемой координаты, k1 постоянный коэффициент.

На рис.1 представлена структурная схема самонастраивающейся системы (СНС).

Дополнительная обратная связь вместе с входящим в него исполнительным устройством в виде интегрирующего звена выполняет функцию контура сигнальной (пассивной) адаптации. Закон управления объектом определяется соотношением u (t) =

k ₂ x 0

t

- x(t) + k 1 - J (x0 — x(t))dt

k.

Коэффициент k 2 < 1 в прямой цепи системы позволяет при больших отклонениях регули-

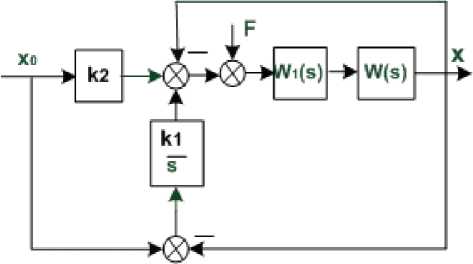
Рис. 1. Структурная схема самонастраивающейся системы:

W(s) – передаточная функция объекта, W ₁ (p)=k – пропорциональный регулятор, k ₁ и k ₂ – постоянные коэффициенты, к 2 < 1 .

X — регулируемая координата; X 0 - уставка

^X(t) . .,

(^- + к 2 ) ■ W (p) ■ W(p)X 0 ^p

k

1 + — ■ W (p) ■ W(p) ^p

p . 0

W (p) ■ W(p) ■ f

к

1 + л ■ W (p) ■ W(p))

= ^X 0

p

p . 0

руемой координаты (например, при пуске, когда x ₀ >>  x ) обеспечить плавный перевод объекта в заданное состояние без перерегулирования. Интегрирующее звено, включенное в контур самонастройки, выполняет автоматическое масштабирование задающего воздействия (уставки) х ₀ в функции ошибки и позволяет при соответствующем выборе коэффициентов k , k ₁ и k ₂, обеспечивающих сходимость процессов в системе во всем ограниченном диапазоне изменения параметров объекта и среды, устранять статические ошибки при действии как задающих, так и возмущающих параметрических и сигнальных воздействий без интегрирующих звеньев в прямой цепи управления. Динамические свойства данной структуры при F(s) = 0 определяются передаточными функциями в замкнутом и разомкнутом в основном контуре состояниях, которые имеют вид (4) и (5):

(к 2 + ^ ) ■ W 1 (s) ■ W(s)

W 3c (s) =-------- k -------------------;    (4)

1 + ( 1 + k ¹ ) ■ W 1 (s) ■ W(s))

s

(k 2 + k ¹ ) ■ W 1 (s) ■ W(s)

^W рс (s) =----^-------------- .   (5)

1 +   ■ W 1 (s) ■ W(s))

s

Записав эти соотношения в операторной форме в виде дифференциальных уравнений, можно показать, используя теорему о предельном переходе, что x 0 = X ( t ) как в замкнутой, так и в разомкнутой (в основном контуре) системах при X о = Const и f = Const.

Передаточная функция разомкнутой системы без контура самонастройки имеет вид:

W рс ( s ) = W 1 ( s ) ■ W ( s ) .            (8)

В линейной системе предельное значение коэффициента усиления, при котором система еще сохраняет устойчивость, определяется в соответствии с критерием Найквиста [1,2] из соотношения (9) путем составления уравнений для мнимых и действительных его частей

A ⁽ jrn ) = ^{— k} пр ,             (9)

где A ( jo ) - характеристический полином частотной передаточной функции (8), k _пр - предельное значение коэффициента усиления, равное k _пр = k ■ k_o , k_o - коэффициент усиления объекта. Предельное значение коэффициента усиления характеризует запас устойчивости системы к действию параметрических возмущений на объект.

Если передаточная функция разомкнутой системы имеет вид k • к

Wpc (s ) =-------------o---------- р       (T1 s +1 )(T2s +1 )(T3s +1) , (10)

то предельное значение коэффициента усиления системы, как произведение коэффициентов усиления регулятора и объекта, получим из решения соотношения (9)

^k пр = , + T 2 + T 3 )(1- + :1 + 17) — 1 .

T ₁ T ₂ T ₃

Для определенности положим

T 1 = 1 сек , T 2 = 0.5 сек , T ₃ = 0.1 сек .

Тогда k _п р = 19.8 .

При этом динамические свойства СНС оказываются не хуже динамических свойств системы, содержащей в основном контуре ПИ-регулятор. Действительно, передаточная функция замкнутой системы с ПИ-регулятором имеет вид

xO) . .

(- 2 + ^к) ■ W(p) ■ W(p)X o

___p__________

1 + ( 1 + ^-) ■ W(p) ■ W(p))

p           J p .

W(p) ■ W(p) ■ f

1 + ( 1 + ^-) ■ W(p) ■ W(p))

= x ; (6)

(k з + ^k4-) ■ W (s)

^W зс ⁽ s ) = -----------^-------------. (11)

1 + (k з + -4- ) ■ W(s))

s

Если приравнять уравнения (4) и (11), то при k 2 = 1

k ₃ = - и , k ₄ = k 1 k           (12)

они совпадают.

При изменении параметров системы в качестве меры робастности используют дифференциальную чувствительность системы, под которой

понимается отношение изменения ее передаточной функции к изменениям передаточной функции (или параметров управления) при условии их малости. Чувствительность замкнутой системы (4) к изменению коэффициента усиления регулятора в основном контуре определяется соотношением [2]:

∂ W W

С "  зс ______ зс 1

^{W 1}     ∂ W 1   W зс

1 + ( 1 + k¹- )W W s

Чувствительность же системы (11) к изменению коэффициента усиления регулятора k ₃ будет иной (в k ₃ раз больше чувствительности системы (4)):

∂ W k        k

V ” зс __ _____ зс 3 __ _____________3____________

^{3    d} k ³ W 3C   1 + ( к 3 + k ⁴) • W

s

Чувствительность системы (11) к изменению передаточной функции объекта W(s) будет равна ности к изменениям параметров управления и затрат на обслуживание.

Нелинейные автоколебательные системы. Большой класс нелинейных автоколебательных систем образуют релейные системы управления, обладающие простотой конструкции, алгоритмической и программной реализацией, высоким быстродействием, надежностью и высокой степенью инвариантности к вариациям параметров объекта [4]. Простейший релейный закон управления при симметричном управляющем воздействии имеет следующий вид:

U _ B • sign ( M ( x )) , (16) где M ( x ) – функция переключения, M(x) _ x 0 — x(t) , sign - знаковая функция, sign ( M ( x ) =1, если аргумент функции больше нуля, и sign ( M ( x ) = -1, если аргумент функции меньше или равен нулю, В – величина управляющего воздействия.

При асимметричном управлении уравнение (16) принимает вид:

∂ W W         1

V ” зс __ _____ 3C __ 1 __ ________________________

W " ⁸ W^W- "1 + ( к 3 + k ) W

s

.

Понятно, что чувствительности систем (4) и (11) к изменению передаточной функции W ( s ) при выполнении условия (12) будут совпадать.

Из соотношений (13) - (15) следует, что чувствительность систем (4) и (11) будет изменяться при изменении параметров объекта. Однако за счет изменения коэффициентов усиления k ₁ и k ₂ она может быть ограничена условиями устойчивости. При этом чувствительность системы (4) будет не больше чувствительности системы (11) к изменению параметров объекта.

Самонастраивающаяся система (4) проще в эксплуатации, поскольку коэффициенты k ₁ и k расположены в разных, невзаимосвязанных контурах и могут настраиваться раздельно с обеспечением желаемых показателей переходных процессов. Следует также отметить, что структура СНС будет решать задачу стабилизации регулируемой координаты с устранением статической ошибки, как это следует из соотношения (7), в условиях обрыва отрицательной обратной связи в основном контуре, то есть она обладает большей “живучестью” по сравнению со стандартными схемами (с ПИ-регулятором в основном контуре). Можно также показать, что система рис. 1 сохраняет структурную устойчивость, если основной контур системы является астатическим.

Следовательно, управление, представленное в системе на рис. 1 оказывается предпочтительней во всех отношениях – отсутствия статических ошибок, запаса устойчивости, чувствитель-

B ,

0,

при M ( x ) > 0, при M ( x ) ≤ 0.

Внешние возмущающие воздействия и асимметричность управления вызывают смещение среднего значения автоколебаний относительно заданного, которое понимается здесь как статическая ошибка. Качество работы релейных автоколебательных систем обычно оценивается по величине амплитуды автоколебаний в установившемся режиме работы, а в переходном - временем затухания колебательных процессов, перерегулированием и числом колебаний, превышающих амплитуду автоколебаний в установившемся режиме работы.

Рассмотрим статику и динамику системы управления рис.1, в которой пропорциональный регулятор W ₁ ( p ) заменен релейным регулятором с законом управления вида (18),

B(t) при M i (x) >  0 , 0 , при M ₁ (x) ≤ 0 .        ⁽¹⁸⁾

где функция переключения

t

Mi (x) _ x о (t) — x(t) _ к2 xо — x(t) + k1 - J (xо — xcp )dt, хср – среднее значение амплитуды автоколе- x + x„ мах min баний, xср _----2----, xмах и xmin – экстремальные значения регулируемой координаты, B( t ) – величина управляющего воздействия,

t

B(t) _ B ₀ + к 3 J (Z — A)dt , B ₀ <  B(t) <  B ₁, (19)

B ₀ , B ₁ – постоянные ограниченные величины, Z – заданное значение амплитуды автоколебаний A = x ₀ - x_э , x_э – экстремальные значения регулируемой координаты.

Таким образом, управление (18) обеспечивает стабилизацию амплитуды автоколебаний и их симметричность относительно уставки в условиях неопределенности параметров объекта и среды путем изменения соответственно сигнала B( t ) и масштабирования уставки.

Гармоническая линеаризация нелинейности (18) при симметричных автоколебаниях и B( t ) = B ₀ приводит к выражению:

W(A)=2⋅B0 .

π⋅A

Значения амплитуды и частоты автоколебаний для заданного объекта определяются из уравнения гармонического баланса [1]:

W ( jω )=

W ( A )

путем составления уравнений для мнимых и действительных его частей.

Понятно, что амплитуда автоколебаний в самонастраивающейся системе при прочих равных условиях в установившемся режиме работы будет не больше, чем в системе без самонастройки. Качественные же показатели и их особенности в переходном режиме в подобных системах проще выявить методом компьютерного моделирования с использованием модели одного и того же объекта (рис. 2).

Из рис. 2, где представлены процессы в релейной (с управлением (17)) и самонастраивающихся системах (с управлением (18)

при B(t) = B ₀ и B(t) в виде соотношения (19) и увели-ченным на 30% коэффициентом усиления системы) с объектом (10), видно, что переключения управления в самонастраивающихся системах происходят в переходном процессе с опережением по отношению к уставке x ₀ . В них существенно меньше перерегулирование, отсутствует статическая ошибка, за счет масштабирования уставки, а время затухания переходных процессов практически не превышает длительности переходного процесса в релейной системе без самонастройки.

ВЫВОДЫ

• 1.    Исследованы статические и динамические свойства робастных самонастраивающихся линейных и релейных автоколебательных систем управления динамических объектов, алгоритмы которых обеспечивают полную инвариантность статических ошибок при постоянных задающих и возмущающих воздействиях без использования интегрирующих элементов в основном контуре.

• 2.    Показано, что запас устойчивости в самонастраивающихся линейных системах не меньше, чем в системах, содержащих интегрирующие элементы в основном контуре.

• 3.    Линейная система с исследованным алгоритмом проще в настройке, ее управление не превосходит по сложности реализации стандартный ПИ-регулятор, и она не теряет работоспособности при обрыве обратной связи в основном контуре.

• 4.    Исследована чувствительность линейных систем к изменению параметров объекта и управления. Установлено, что чувствительность самонастраивающихся систем к изменению в ограни-

  

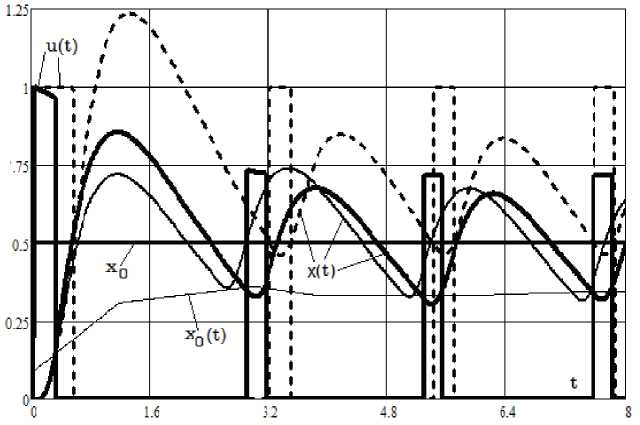
  Рис. 2. Процессы в замкнутых релейных системах (объект (10): сплошные тонкие и утолщенные линии соответственно – самонастраивающиеся системы, в которых B( t) = B ₀ и в виде соотношения (19) при увеличении k_o на 30%, пунктирные – релейная система с управлением (17), k ₂ = 0.1 )

  
  

• 5.    Показано, что качественные характеристики переходных процессов в самонастраивающихся системах с исследованными алгоритмами в условиях параметрических и сигнальных возмущений оказываются не хуже, чем в системах, использующих стандартные управляющие устройства, а по некоторым показателям (в автоколебательных системах) существенно их превосходят.

• 6.    Исследованный самонастраивающийся алгоритм управления релейными системами обеспечивает стабилизацию амплитуды автоколебаний и их симметричность относительно уставки в условиях неопределенности параметров объекта

ченном диапазоне параметров объекта при прочих равных условиях не больше, чем в системах содержащих ПИ-регулятор и существенно меньше – к изменению коэффициента усиления управления в основном контуре.

и среды путем изменения соответственно сигнала управления и масштабирования уставки.