Робастный метод построения линейной регрессии между двумя физическими величинами с учетом их случайных погрешностей

При работе с разными массивами данных часто возникает необходимость нахождения коэффициентов линейной регрессии между двумя случайными физическими величинами. В большинстве случаев коэффициенты регрессии имеют конкретный физический смысл и для корректной интерпретации полученных результатов очень важно найти их значения наилучшим образом.

Существует несколько формул для определения коэффициентов регрессии [1–3], но не для всех формул есть общее понимание, в каких случаях их следует использовать. В настоящее время отсутствует единый подход к нахождению коэффициентов линейной регрессии для общего случая, когда разброс точек в корреляционной связи между двумя величинами обусловлен как их случайными погрешностями измерений, так и неконтролируемыми физическими факторами.

Постановка задачи. Рассмотрим две случайные физические величины X 0 и Y 0 , между которыми существует статистическая корреляционная связь. Предположим, что эта связь может быть описана линейной зависимостью

Y 0 = K 0 + K 1 X 0 . (1)

Требуется найти коэффициенты регрессии K 0 и K 1 , которые наилучшим образом отражают физическую взаимосвязь между ними.

Так как X 0 и Y 0 измеряются со случайными погрешностями, то на практике мы имеем дело с величинами X и Y , для которых уравнение регрессии запишется в виде

Y = K 0 + K 1 X . (2)

Запись уравнений (1) и (2) с одинаковыми коэффициентами регрессии показывает, что последние не должны зависеть от случайных погрешностей измеренных величин X и Y. В дальнейшем будем говорить о нахождении только коэффициента регрессии K1, так как K0 вычисляется после нахождения K1 по известной формуле к0 = Y - к 1 ■ X, (3)

где X и Y – средние значения X и Y .

Новый подход к нахождению коэффициента регрессии K ₁ . Этот подход заключается в следующих моментах:

– случайные величины X и Y нормируются на значения ^5 X + 5 X и ^5 Y + 5 Y соответственно, где 5 X и 5 Y - случайные среднеквадратические погрешности измерения X и Y для рассматриваемого массива данных; 5 X и 5 _Y - некоторые величины, характеризующие разброс точек в корреляционной связи физических величин X ₀ и Y ₀ за счет неконтролируемых физических параметров;

– при нахождении коэффициента регрессии K ₁ используется ортогональная среднеквадратическая регрессия, т. е. минимизируется сумма квадратов отклонений, перпендикулярных искомой прямой.

Тогда уравнение линейной регрессии запишется в виде

2            22

В = 1-р   .Л-— Y-)= 1-Ip I. --- ^{5 Y} /^{с Y}

B А¹ |^{р х} о ^Y >| (1 -2) А^{1 р XY} \ 152/2

V                  ^с Y )           V     ^Ux/ ° X

. (13)

Используя (10) и (11), уравнение линейной регрессии (4) запишем в виде

У '    ' X

,         = к 0 + K 1 ■ ,

V⁵^⁵”         V⁵ X ⁺⁵ X о

.

Y с Y ■ B

_ '     ' X

= Kо + K1--- с Х ■ A

.

Здесь величины 5 _х и 5 _Yg находятся из решения системы двух уравнений:

– первое уравнение имеет вид

|^Р X о Y о | ■ ^С X о ■ ^С Y , = V ^С Х о — ⁵ Х о " V° Y — ⁵ Y о ,        ⁽⁵⁾

где сх =  сХ — 5Х и сY =  сY — 5Y — среднеквадра тические отклонения величин Xо и Yо; сх и сY - среднеквадратические отклонения величин Хи Y; рX.Y^ -коэффициент корреляции между X0 и Y0. Коэффициент корреляции рх Y находится из известного уравнения [1]:

р XY ^с X ^с Y = р X о Y о ^с X о ^с Y о ^{,              (6)}

Уравнение (14) легко привести к виду (2):

Y = Ko '■с,^ B + K '■^Y^B ■ X = K + K ■ X ,(15)

о Y 1 с X ■ A где kо = kо'^ A ■с Y ■ в;(16)

K1 = K1 ■^Y--.(17)

с _X ■ A

Применяя ортогональную среднеквадратическую регрессию к уравнению (14) и используя соотношение (17), получим выражение для искомого коэффициента регрессии:

с_у B 1

K1 = —-----x с X A 2 ^р XY

где р _XY - коэффициент корреляции между X и Y . Заметим, что из уравнения (6) следует уравнение (5);

– второе уравнение запишем в виде

x

A

B

B

A

A

B

B

A

+ 4■P XY ^

, (18)

5Х    5У х о = Y о с V   с у

X ₀        Y ₀

и назовем условием пропорциональности величин 5 у , 5У и с у , с у . Введение величин с у , су и за-

X ₀      Y ₀        X ₀ Y ₀                                   X ₀ Y ₀

пись условия (7) являются ключевыми моментами, так как это позволяет получить обобщенное решение для коэффициентов линейной регрессии уравнения (2).

Результаты. После решения системы уравнений (5) и (7) имеем:

⁵ X о

= ^с X ■

5У

Y ₀

= ^с y ■

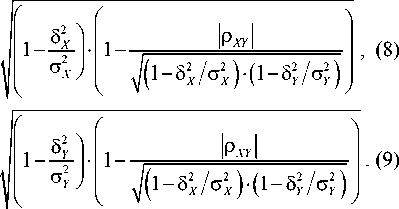
(8) и (9) найдем значения ^5 Х + 5 Х_о и

где А и В определяются выражениями (12) и (13).

Впервые формула (18) была представлена в [4], а подробно описана в [5].

Анализ полученных результатов. Выражение (18) позволяет устанавливать однозначную связь между величинами X и Y и определять условия использования известных типов линейной регрессии.

Покажем, что все известные аналитические выражения для коэффициента регрессии K ₁ уравнения (2) являются частными случаями формулы (18).

Так, для случая когда разброс точек в корреляционной связи X и Y обусловлен только их случайными погрешностями, т. е. рХ Y = 1, получим выражение для коэффициента регрессии K1, приведенное в [1]:

K 1 =^—

⁵ X ² ■ ^р XY

^с Y ⁵ X — ^с X ⁵ Y

—

Y

5 Y —

5 х

I ^с y ⁵ х   ^с X ⁵ Y I , д 2

II + 4 ■ р XY

( ^с х ⁵ Y ^с Y ⁵ X )

С учетом

V ⁵ -5 Y :

При р _{х о Y} о = 1, 5 _х = о и 5 _Y * о имеем

где

V ⁵ X ⁺⁵ X о

V⁵ Y + ⁵ Y

= ^С X ■ A ,

= с Y ■ B ,

A = А ¹ — |^р X о Y о Р ⁽¹ - А =

V               ° X

1-|р I. ^{1   5} X^X -

I^р XY | А 1   22 /^2 ^;

V 1 —5 Y / с Y

к 1 = lim■    ¹    ■; " ^с - ■^ Х — Я х А) +

^{5 x} ^ ^{о 5} х ² -^р XY К^с X ⁵ Y ^с Y ⁵ X J

—

^с X

⁵ X .XyL ⁵ Y I 1 , 4 „2    | ^с Y ⁵ X

--1---- I 1 + 4 ■ р _XY ■ I---

⁵ Y ^с Y ⁵ X Л         1 ^с X ⁵ Y

Разлагая выражение под квадратным корнем в ряд Маклорена [6] и оставляя первые два члена, получим

Зу 1     || Gy Зу Gy Зу

K . = lim —----^1 — ■ — —- ■ —

З т ^ о х    2 ■ о су    8      су   8

°X ^р XY  ^W X ^иУ   ^G Y °х.

	2
, f G Y 3 X ,X X  3 Y ) +111	1       П 2 I G Y 3 X | 1 + 2 ■ р XY |1	>= (20)
V G X  3 Y G Y  3 X )	_          V G X 3 Y J _	I

XY .

Gy — ■Р

G _X

Это известная формула для коэффициента K ₁ уравнения прямой регрессии Y = K ₀ + K ₁ X , которая находится путем минимизации суммы квадратов отклонений вдоль оси Y от искомой прямой [2].

При р XY = 1, З _Y = 0 и З _X * 0

(23) можно рекомендовать к использованию при отсутствии информации о величинах случайных погрешностей X и Y . Заметим, что эта формула представляет собой среднее геометрическое формул (20) и (21).

Диапазон изменчивости коэффициента регрессии. Для случая когда разброс точек в корреляционной связи величин X и Y обусловлен только их случайными погрешностями, т. е. р _XgYg = 1, коэффициент регрессии будет изменяться в следующих пределах:

^^ ■р xy| ^ K 11 ^G X

^G Y    ¹

Ь: ------- ■ 1--------7 ,

^G X |р xy|

а при р _{X Y} < 1 - в пределах

Зу     1     l| Gy Зу Gy  Зу

K. = lim —----^1 — ■ — —- ■ — зy^0Х    2-0 I су 8 су   8

^U X     ^р XY L\ X Yy   ^G Y Xx .

^ ■Р xy| <  K 1| <^^ ■ Д.

^G X                ^G X |р xy|

+

G _Y

■

З X

—

G _X

■

З Y

G _X

З Y

G _Y

З X

1 + 4 ■р

XY

■

^G X

■

З Y

.

^G Y

З X

.

Проведя процедуру разложения выражения под квадратным корнем в ряд Маклорена [6] и оставляя первые два члена, получим

Зу 1 l| Gy Зу Gy Зу

K , = lim —----^1 — ■ — —- ■ —

^{3 Y} >⁰ Зу  2 ■руу   (Gy  Зу   Gy  Зу

X      XY      X Y Y   X

+

^G Y

^G X

3 X

■------------

3 Y

X

Y

3 Y ■------------

3 X

^{1 + 2} ^ ^p XY

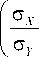
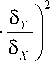
= _G r_ ■ ^G X Р XY '

Формула (21) – также известная формула для коэффициента 1/ K * уравнения обратной регрессии X = K ₀ * + K * ■ Y , которая получается путем минимизации суммы квадратов отклонений вдоль оси X от искомой прямой [2].

При р _{X Y} = 1 и 3 _X = 3 _Y * 0 для коэффициента K ₁ уравнения ортогональной регрессии Y = K ₀ + K ₁ X получим формулу

K

Из выражений (24), (25) следует, что коэффициенты для прямой и обратной регрессий принимают соответственно минимальное и максимальное значения.

Кратко сформулируем основные выводы:

– получена обобщенная формула, позволяющая находить коэффициенты регрессии линейного уравнения Y = K 0 + K 1 X при условии, что разброс точек в корреляционной связи случайных величин X и Y обусловлен как их случайными погрешностями измерений, так и неконтролируемыми физическими факторами;

– все известные выражения для коэффициентов регрессии являются частными случаями полученной формулы. Определены условия использования данных выражений;

– обобщенная формула позволяет получать робастные, достоверные и физически корректные коэффициенты регрессии. Эта формула представляет интерес для специалистов, занимающихся обработкой разных массивов данных и может быть использована для их корректной физической интерпретации, независимо от области знания.

² ^ ^р XY

■

^G Y

^G X

—

^G X

^G Y

+

^G Y

^G X

—

^G X

^G Y

+ 4 ■р

XY

^, (22)

которая определяется путем минимизации суммы квадратов отклонений, перпендикулярных искомой прямой [3].

Если для массива данных выполняется соотношение -^X- = — , то из выражения (18) вытекает простая G X  G Y формула для коэффициента регрессии:

K 1        .                       (23)

^G X 3_X   3y

Так как соотношение -^ =    выполняется для

G X G Y большинства экспериментальных данных, то формулу