Роботизация ремонта дорожного покрытия

Робот, который способен отсканировать дорожное покрытие на наличие повреждений и устранить их, предполагает использование спутниковой системы для передачи точных координат участка дороги, а также для контроля процесса ремонта дорожного покрытия человеком. В функции машины входит ремонт дороги способом частичной замены верхнего слоя дороги, а также заполнение недостающего слоя асфальтом (рис. 1).

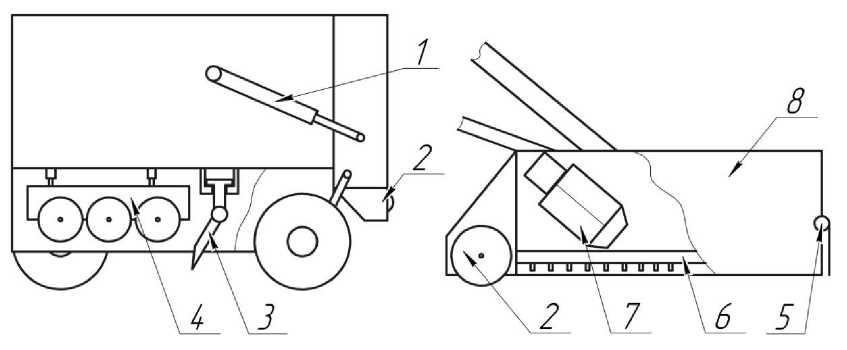
Рис. 1. Модель робота

Благодаря тому что робот самостоятельно ремонтирует дорожное покрытие, значительно ускоряется процесс ремонта дороги и уменьшаются расходы. В устройство робота входит гидроцилиндр 1, за счет которого платформа 8 плавно опускается на поверхность дороги. В центре платформы находится турбина 7, которая продувает поврежденный участок дороги. В нижней части расположен нагревательный элемент 6, разогревающий поверхность асфальта до 120° C. На задней части имеется барабан 2, который позволяет разрыхлить разогретый участок дорожного покрытия за счет игольчатой поверхности, а на передней – за- слонка 5, открывающаяся при продувке ямы, благодаря чему весь мусор удаляется наружу. В центре робота находится манипулятор 3, который принимает показания бортового компьютера о форме повреждения дорожного покрытия и глубине ямы и заполняет участок асфальтом в определенном объеме. Позади манипулятора имеется виброкаток 4, который уплотняет и выравнивает ремонтируемую поверхность.

При эксплуатации робота его транспортируют на участок дороги, который необходимо отремонтировать. Координаты данного участка робот получает через спутниковую связь. При этом он обозначается специальной световой сигнализацией и знаками. Далее робот сканирует поверхность дороги в попутном направлении движения транспорта на наличие повреждений и при их обнаружении останавливается, опуская платформу на яму. Идет продувка от мусора, и после завершения осуществляется прогрев до 12° С. После этого робот, не поднимая платформу, начинает движение, автоматически включая барабан, который обрабатывает нагретую поверхность. Одновременно датчик сканирует яму, определяя ее контур и глубину. Платформа поднимается. Получая данные с датчиков, бортовой компьютер определяет схему движения манипулятора и количество требуемого асфальта. Манипулятор, получив сигнал от компьютера, укладывает асфальт. Минимальная температура укладки асфальта +10° С, температура асфальта 120° С, слой асфальта должен быть выше уровня поверхности дороги на 2 3 см. Далее, по ранее заданной программе, робот продолжает движение и опускает виброкаток, который выравнивает и утрамбовывает участок покрытия. Через спутниковую связь ставится отметка на карте для контроля качества и долговечности. Далее цикл повторяется.

При эксплуатации роботов часто возникают вибрации, которые приводят к снижению точности и эффективности выполнения заданных операций. Причина этого заключается в том, что предположение о жесткости конструкции робота часто оказывается слишком грубым. Проблема управления гибкими манипуляторами имеет огромное значение. Ниже предложен метод управления одно- и двухзвенным манипулятором с учетом гибкости его звеньев и соединений между ними.

Модель звена робота изображена на рисунке 2.

У

Е1

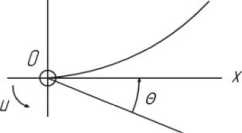
Рис. 2. Модель звена

Она представляет собой стержень, один конец которого связан с неподвижной точкой О. Стержень может вращаться относительно неподвижной точки под действием управляющего момента U. Система координат X, Y связана со стержнем и вращается вместе с ним. Дальше рассматриваем только те колебания системы, которые вызваны наличием момента изгиба. Уравнение Эйлера для вращающегося стержня имеет вид:

dzy     д*у рА^^Е1й—-^ = й at?      ох* ,

где р – плотность; E – модуль Юнга; ^а — момент инерции площади поперечного сечения; A – площадь поперечного сечения; y (x, t) – отклонение стержня от оси X в точке x в момент времени t.

Краевые условия для уравнения (1) задаются соотношениями:

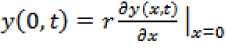
a^yC^t) I _ БГдг а²у I St² L=0 j_s 5^2 Lr=O

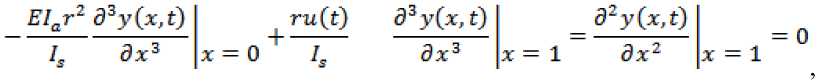
где I – длина стержня; r – радиус соединения; ^5 – момент инерции стержня. Воспользуемся

методом разделения переменных и будем искать решение уравнения (1) в виде y (x,

t)=a(t) (x), где  (x) – функция моды.

Из (1) и (2) получаются следующие уравнения и краевые условия:

''''(x)-к4ф(лг) = 0                       | с5к*ф^ +--^ (0) - —(0) = 0

0(0) - гф^№> = 0

,

2         L4

C = ""7 '

где     pA - положительная контстанта.

Функции мод 02 (x) должны удовлетворять условию ортогональности: Д¹ Ф1 (х^ф^йх + ^ф' /о)ф'_;(0) = <5у.

Из (3), (4) можно получить уравнение собственных чисел , имеющее счетное количество решений Я^ = /с ^/5 i = 1,2,..... . Чтобы получить динамические уравнения, которые можно было бы использовать для моделирования движения робота, ограничимся конечным числом N мод 0 г И- Движение стержня, рассматриваемого как абсолютно твердое тело, является составляющей общего движения системы и описывается соотношением:

gLdW = v^(t).

где ^ — ^а "^" ^5 . Если уравнения для функций времени ajCOG = I-»), которые выводятся из (1), рассмотреть совместно с соотношением (5), то будет получено следующее матричное уравнение:

£(t) = ЛХ(0 4- ЬиУГ),(6)

Вектор выходных характеристик следующим образом выражается через вектор состояний:

y=CX.(7)

Уравнения (6) и (7) являются уравнениями движения модели звена робота. Входящая в них функция управляющего момента может быть определена одним из двух способов:

u = rd- Ку(у - ут);(8)

^ = гй-Кя(Х-Хт-),(9)

где rd значение управляющего момента, рассчитанное при планировании движения; yr – заданный вектор выходных характеристик, который должен быть реализован системой управления; X – оценка вектора состояний X; Xr – заданный вектор состояний.

Были проведены эксперименты, в которых изучалось поведение звена робота, обладающего одной степенью подвижности, при использовании управлений вида (8) и (9). В начальный момент времени робот совершал колебания с основной частотой 0,6 Гц. Целью управления являлась стабилизация заданного положения робота. В этом случае контролировать возникающие на движениях системы колебаний можно с помощью управления вида:

иг = rdi - ^(^ - ^rz) (f = 1,2).                           (10)

Для учета изменения момента инерции двухзвенника во время его движения коэффициенты обратной связи в (10) выбираются в соответствии с адаптивным законом регулиро- вания:

кц(Й = кц (0) - Эрц бц (О^ц (t)

Siu £ ^eu МУМ              (11)

Схема экспериментальной установки, предназначенной для изучения поведения звена робота с двумя степенями подвижности, изображена на рисунке 3.

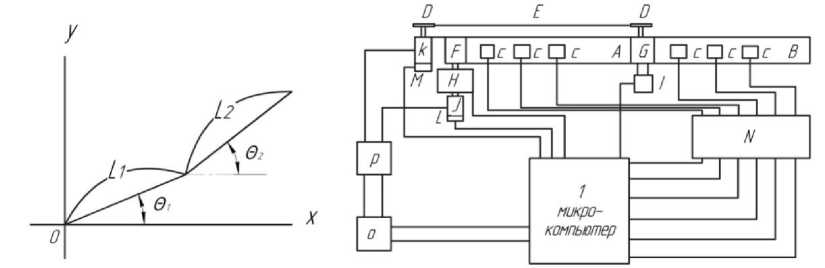
Рис.3. Схема установки где 1 – микроЭВМ; А – гибкое звено 1; В – гибкое звено 2; С – датчики напряжений; D – шкив; E – тросовая передача; F, G – соединения звеньев; H, I – датчики углов поворота; J, K – двигатели постоянного тока; L, M – тахогенераторы; N, O, P – усилители.

В процессе экспериментов осуществлялось позиционирование робота, первое звено которого совершало главные колебания с частотой 5 Гц, а второе с частотой 1 Гц. При этом использовалось управление, рассчитанное на абсолютную жесткость конструкции робота и построенное с учетом гибкости звеньев. Закон характеризуется минимальным временем переходного процесса и максимальной точностью позиционирования. Поскольку предложенный вид управления звеном робота вызывает затухание присутствующих в системе колебаний, это управление можно использовать для увеличения жесткости робота наряду с увеличением жесткости его механической конструкции. Кроме того, описанный вид управления может быть успешно применен для погашения колебаний манипулятора, возникающих при его соударении с внешними препятствиями. Один из подходов к управлению манипуляционным роботом в условиях знания его динамической модели и инерционных характеристик объекта манипулирования заключается в использовании методов адаптивного управления. Предлагается алгоритм управления с идентификацией неопределенных параметров, являющийся развитием метода управления.

Манипулятор рассматривается как последовательная цепь n звеньев. Управление движения манипулятора может быть представлено в виде