Robust Chaotic Digital Image Watermarking Scheme based on RDWT and SVD

Published Online August 2016 in MECS

Copying and distributing multimedia data such as image, video, audio or text is not difficult in today’s internet era. As a result, encryption and digital watermarking have been proposed as complementary solutions to protect multimedia data. In encryption, original signal is protected by a predefined method during the transmission. However, the signal is not protected anymore once it is decrypted. Digital watermarking methods, on the other hand, embed a secret key called watermark into the original signal.

The most popular applications of digital watermarking are copyright protection, broadcast monitoring, fingerprinting, authentication checking, usage control and information hiding. Although different watermarking applications need some specific requirements, the three common requirements desired for the most applications are fidelity (or invisibility), capacity and robustness. Unfortunately, there is a tradeoff between these requirements. For example, a stronger watermark can be used to increase the robustness, but in this case watermark becomes noticeable. On the contrary, increasing the capacity decreases the robustness. Consequently, one must make a choice between these three requirements according to the application [1].

Digital watermarking techniques can be classified into several categories. One classification is made according to the embedding domain. In spatial domain techniques, the secret data is directly inserted into the samples of the cover signal. In frequency domain techniques, embedding process is performed in the frequency domain by modifying the transform coefficients. Another classification is made based on the type of the document: text, image, audio and video watermarking schemes. Finally, from the human visual system point of view, watermarking methods can be divided into three groups namely visible, invisible-robust and invisible-fragile methods. The robust watermarking schemes can be further divided into four sub-groups. In private watermarking, the original signal and the secret key used to embed watermark are required for watermark detection. Semi-private watermarking schemes give only the information whether the watermark is present or not. So, they do not need the cover signal for detection. In public (also known as blind) watermarking schemes, the cover signal is not used during watermark decoding. At last, watermark decoding process and public key are assumed to be known by anyone in the symmetric watermarking method. However, the public key is not used neither to compute secret key nor remove the watermark [1-3].

There are numerous digital image watermarking algorithms in the literature. The references [4, 5] are examples of spatial domain techniques whose main advantage is their lower computational complexity. However, transform domain techniques are more robust than spatial domain techniques against both image processing and geometrical attacks. Discrete Fourier Transform (DFT), Discrete Cosine Transform (DCT), Discrete Wavelet Transform (DWT), Complex Wavelet

Transform (CWT) and Redundant Wavelet Transform (RDWT) are the most commonly used transformations for frequency domain filtering. SVD is combined with one of these transforms to improve the robustness and imperceptibility of the watermarking schemes. Recently, SVD has become a prominent tool in digital image watermarking. SVD can be directly applied to the data matrix and it provides quantitative information about the structure of the system [6]. The slight variations in the singular values of images are not perceived by the human visual system. This is the main idea behind SVD based image watermarking algorithms.

An adaptive watermarking algorithm using wavelet domain SVD is proposed in [7], where a simple quantization-index-modulation process on the wavelet domain SVD is applied. The method is robust against JPEG compression but extremely sensitive to malicious manipulations such as filtering and adding random noise. A hybrid image watermarking scheme based on DWT and SVD is proposed to satisfy both imperceptibility and robustness requirements in [8] in which the watermark is embedded on the elements of singular values of the cover image’s DWT sub-bands. In [9], the authors proposed a hybrid watermarking technique using SVD with orthogonal transforms. SVD is combined with wavelet transforms generated from orthogonal transforms. Behavior of proposed method is evaluated against various attacks. A color image watermarking scheme using DWT is presented in [10]. The other watermarking schemes based on DWT and SVD can be found in [11-17]. In recent years, RDWT is an emerging transform domain technique in digital image watermarking schemes. It is known that RDWT based algorithms provide resistance against noise attacks due to its shift invariance property. Furthermore, the robustness against the affine transformations and simple cover and watermark extraction property are other advantages of the RDWT. In [18], a RDWT and SVD based image watermarking scheme is presented. The scheme is evaluated against image processing and geometrical attacks. In [19], a RDWT and SVD based non-blind image watermarking method that is robust against affine transformations and ordinary image manipulations, is proposed. Its performance is compared to that obtained by DWT-SVD based methods. A similar RDWT-SVD based method is also given in [20].

As a result of the discussion given above, in this study a digital image watermarking technique is developed based on RDWT and SVD. The proposed scheme is combined with chaos to improve the robustness and perceptual invisibility. Using a chaotic signal as the watermark allows the proposed scheme to meet the security requirements as well. To evaluate the performance of the proposed method, recent chaos based digital watermarking methods are investigated. The proposed method is compared to existing chaos based digital image watermarking schemes to show its superiority. In [21], a DWT based digital image watermarking scheme using chaotic encryption is given. Quality of the watermarked image is measured by NC and PSNR. A robust chaotic digital watermarking method is proposed in [22] where Chebyshev maps are used to generate substantially different watermarks. The algorithm is based on multi-wavelet and SVD. In [23], a DWT based chaotic watermarking algorithm is proposed to improve embedding capacity and anti-detection ability of watermarking. A hybrid DWT, SVD and logistic chaotic map based watermarking technique is proposed to satisfy both imperceptibility and robustness requirements in [24]. The goal of this study is to solve false position and watermark rounding error problems in the frequency domain. In [25], DWT, SVD and Walsh based digital image watermarking algorithm is proposed. The authors show that the method is efficient against geometric attacks. Another scheme which makes use of the visual cryptography, transform domain, chaos, noise reduction and error correcting code techniques is given in [26]. A non-blind DCT, cross-chaos and Arnold map based watermarking method is presented in [27]. The robustness of this method is evaluated against JPEQ, scaling and white Gaussian noise attacks. In [28], the authors proposed a technique for watermarking in combined spatial and frequency domains based upon chaotic maps. The robustness of the scheme is measured for noise, compression and cropping attacks. Chaos game representation, normalization and DCT Based watermarking algorithm that can resist geometric attacks is discussed in [29]. It is shown that the algorithm is invisible and robust against geometric attacks. In [30], DWT-SVD and Arnold cat map based watermarking algorithm is proposed. This method is performed under rotation, noise and JPEQ compression attacks.

Almost all of the chaotic digital image watermarking methods are based on DWT and SVD. To the best of our knowledge, there do not exist any digital image watermarking scheme combining RDWT, SVD and chaos. In order to provide increased performance, we offer a hybrid digital image watermarking algorithm in this study. At first, RDWT is applied to the cover image resulting in sub-bands of the cover image. On the other hand, a chaotic image matrix having the same size as the cover image is generated by using a chaotic mapping function. It is added to the LL sub-band of the cover image. Then, SVD is performed for both the resulting matrix and the sub-bands of cover image in order to achieve the embedding process. Finally, inverse SVD and inverse RDWT are performed, respectively to obtain the watermarked image.

The study is organized as follows. In Section 2, RDWT, SVD and  chaos  are reviewed. The proposed watermarking scheme is described in Section 3. Experimental results are given in Section 4. Finally, Section 5 concludes the paper.

• II.    Background Information

In this section, background information about RDWT, SVD and chaos is given to better understand the proposed digital image watermarking method. They are also discussed from the image watermarking point of view.

• A.    RDWT

DWT is a useful tool in image processing applications to transform the image from spatial domain to frequency domain. It provides sufficient information to analyze and synthesize the data with a significant reduction in the computational complexity. However, the down-sampling process in DWT makes it shift-variant even for small shifts in the input image. This is the main drawback of DWT based method watermarking schemes. The shiftvariance of DWT causes inaccurate extraction of the cover image and the watermark. This problem is avoided by using RDWT also referred as “undecimated DWT”, “overcomplete DWT” and “algorithme à trous” [31]. The use of RDWT for image watermarking is very promising since the redundancy obtained by the transform is more robust in carrying watermarking data. Difference between the DWT and RDWT are demonstrated in the following discussion where f [ n ] and f ’[ n ]represent the input and reconstructed signals, h [- k ] and g [- k ] are the low-pass and high-pass analysis filters while the corresponding low-pass and high-pass synthesis filters are h [ k ] and g [ k ], the low-band and high-band output coefficients at level j are denoted by c j and d j , respectively [21].

DWT decomposition coefficients can be expressed as

Cj [к] = (c j+i[k] * h[-k]) I 2(1)

dj[k] = (di+1[k] * h[-k]) I 2(2)

where * and 1 2 indicate the convolution and downsampling with a factor two. That is, if y[n] = x[n] I 2 then

y[n] = x[2n](3)

At the synthesis level, the reconstruction equation can be written as

C+i[k] = (Cj[k] t 2) * h[k] + (dj[k] t 2) * g[k] (4)

where t 2 is the up-sampling with a factor two. That is, if y[n] = x[n] t 2 then

y[n]=(# ^{П 6}"'^ \  0, n оdd

As we pointed out before, RDWT eliminates the downsampling and up-sampling at each step. Thus, the filters themselves are up-sampled to adopt the length of the growing data. Particularly, the corresponding filters for scale j are hj[k]=hj+J k] t 2(6)

9j [k] = gj+1[k] t 2(7)

The 1D RDWT analysis and synthesis equations are given as follows

Cj [k] = ( c+i[k]*hy[-k])(8)

dj [k] = (dj+i[k]*ay[-k])(9)

with

C+i = 1 (C [k] * h [k] + d[ [k] * g[ [k])(10)

Equations (6)-(10) conclude the discussion.

• B.    SVD

SVD is an efficiently used technique in image and signal processing applications such as compression, data hiding, noise reduction and watermarking. The vast majority of the digital image watermarking schemes in the literature combines SVD with DWT. SVD can be applied directly to a digital image of any size. Given a data matrix A having W linearly independent columns (i.e. rank ( A ) =W), there are two unitary matrices V and U such that

A = USV^T               (11)

where S = diag (σ₁, σ₂, …., σ_W) is a diagonal matrix. Singular values (σ’s) are ordered as σ₁≥ σ₂≥…≥σ_W>0. This equation is the mathematical statement of the SVD theorem and also referred as Autonne- Eckart- Young theorem [6].

SVD is an optimal decomposition concentrating the maximum signal energy into as few coefficients as possible. From the image processing point of view, main advantages of SVD can be summarized as follows: i) input matrix does not have to be a square matrix, ii) SVD provides information about an image where singular values correspond to the brightness of the image and U and V denote the geometric properties of the image, iii) the slight variations in singular values of an image is not detected by the human visual system. The last property is the main reason why SVD is preferred for watermarking applications [32].

• C.    Chaos

Chaotic signals satisfy the important property of complexity required for secure communications. Complexity in the context of a chaos theory can be described as the impossibility of regenerating a chaotic signal without knowing its initial value. As a result, chaotic signals can be exploited in digital image watermarking schemes to meet the security requirements.

There are several mapping functions to generate a chaotic sequence [33]. The most common one dimensional chaotic maps are the saw tooth map, tent map, Chebyshev map and logistic map. These maps are defined on the unit interval [0, 1]. In our study, the chaotic sequence is generated by using the logistic mapping function given by

x [n] = /_г(х[п - 1]) = Ax[n - 1](1 - x[n - 1]),Л = 4.

where λ is called as bifurcation parameter of the chaotic map. Note that, in Eq. (12) it is assumed that the chaotic signal at iteration n is determined by its previous value at iteration n-1. In general, the value of the chaotic signal at any iteration depends on its past d values. For this case, mapping function takes the form x[n] = f (x[n-1], x[n-

2],…, x [ n-d ]), where d is referred as the embedding dimension of the chaotic system. In this study, the embedding dimension of the logistic mapping function is assumed to be equal to one.

(a)

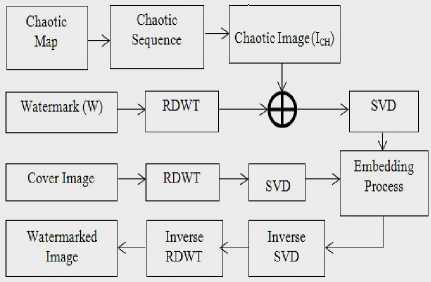
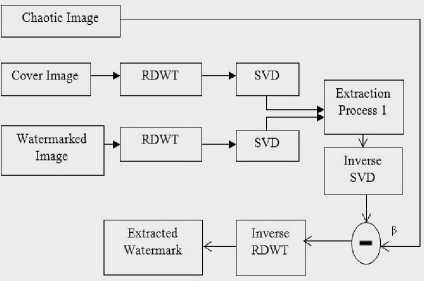
Fig.1. The proposed method. (a) watermark embedding process, (b) the watermark extraction process.

(b)

• III.    Proposed Chaotic Watermarking Algorithm

A general watermarking system consists of two main units: the watermark embedding unit and the watermark detection/extraction unit. Both units can be considered as a separate process. In the following subsections, watermark embedding and extracting processes for the proposed method are explained.

• A.    Watermark Embedding Process

The steps of the proposed embedding algorithm illustrated in Fig. 1(a) are as follows:

Step 1 : Generate a chaotic sequence with the logistic map given in Eq. (12). Size of the chaotic sequence is m x n . Then, construct the chaotic image matrix by arranging the chaotic sequence so as to have same dimensions with the watermark.

Step 2 : Perform RDWT to decompose the watermark into the four sub-bands LL, LH, HL and HH.

Step 3 : Obtain the weighted sum of the LL sub-band of the watermark image and chaotic image matrix as follows:

W_CH = W_LL+PI_CH          (13)

where W CH is the chaotic watermark, WLL is the LL subband of the watermark, ICH is the chaotic image matrix obtained at the end of the first step and β is the chaos scaling factor.

Step 4 : Apply SVD to the W _CH

W _CH = u^w S^w V^wT           (14)

Step 5 : Decompose the cover image to the LL, LH, HL and HH sub-bands by using RDWT,

Step 6 : Apply SVD to each sub-band of the cover image to obtain

IC = U^l S^l V^lT                  (15)

where i denotes the LL, LH, HL and HH sub-bands, respectively.

Step 7 : Replace the singular values of W _CH by the singular values of IC as follows

S^l * = S^l + aW^w               (16)

where S ¹ and S^w are the diagonal singular value matrices of IC and W _CH, respectively and a is the scaling factor determining the weight of the chaotic watermark on the embedding process.

Step 8 : Apply inverse SVD to the transformed cover image with the modified singular values to obtain

IC1 = u1 S1* V1T                   (17)

Step 9 : Perform inverse RDWT to get the watermarked image.

• B.    Watermark Extraction Process

The watermark extraction process given in Fig. 1(b) can be explained as follows:

Step 1 : Perform RDWT on the watermarked image I*, (may be subject to the distortion) and decompose it to the LL, LH, HL and HH sub-bands.

Step 2 : Apply SVD to each sub-band:

Iw = U ¹ S *V^lT                (18)

where i denotes the LL, LH, HL and HH sub-bands of the watermarked image.

Step 3 : Extract the singular values by using the frequency sub-bands of the watermarked image and cover image as follows:

S^w * = (S¹*-S¹)/ a               (19)

where Sl* and S1 are the diagonal singular value matrices of the watermarked image 7^ and the cover image IC for sub-band i (i.e. LL, LH, HL and HH), α is the scaling factor used in the embedding process.

Step 4 : Apply inverse SVD in order to obtain modified chaotic watermark image W^_H .

Step 5 : Derive the low frequency coefficients of the watermarked image from

W tL = W*CH-piCH             (20)

where W L_l and WC_H are the LL sub-band of the watermarked image and the modified chaotic watermark image. β is the chaos scaling factor used in the embedding.

Step  6: Perform inverse RDWT to obtain the watermark image.

• IV.    Simulation Results

In this section, performance of the proposed watermarking method is evaluated by using computer simulations. Four gray scale images of size 256x256 known as Lena, Pepper, Baboon and Airplane are used in the simulations. The watermark is also a gray scale image (Cameraman) with the same size as the cover images. The scaling factors α and β are chosen as 0.25 and 50, respectively. Note that increasing the chaotic scale factor β makes the watermark more secure but in this case imperceptibility of the watermark decreases.

The main goal of the proposed RDWT-SVD based chaotic image watermarking scheme is to improve robustness and imperceptibility obtained by the existing methods. The watermarked image should satisfy the imperceptibility requirement that is measured by peak signal-to-noise ratio (PSNR) given by:

PSNR = 10log_1Q p®»!]      (21)

where the mean square error (MSE) is defined as:

MSE = -L-^.^xaj) - Yjijyf   (22)

In Eq. (22), size of the images are m x n . Robustness, another desired property for the watermarking schemes, implies the ability of detecting watermark under various types of intentional or unintentional attacks. The normalized cross-correlation (NC) is used to evaluate the robustness of the watermarking scheme. It is computed from:

^k^i^'j_1VW(kj)w,(kj)] j№lxj~iW(kn^ Jl^iZjLjw'Ckj)]2

where W and W' represent the original and extracted watermarks, respectively. The correlation coefficient takes on values in the interval [-1, 1]. If it is near 0, the extracted watermark is completely uncorrelated with the original one. Generally, the NC is considered acceptable if it is 0.75 or above [2, 34].

In Experiment 1, DWT-SVD based chaotic watermarking scheme is compared to the methods in [21] and [35] to emphasize the contribution of SVD to the watermarking scheme. In [21], a DWT based chaotic digital watermarking scheme is proposed. DCT is performed on the copyright protection scheme in [35]. The logistic map is used to generate chaotic image matrix for both studies. Performances of the algorithms are demonstrated under several attacks. Table 1 illustrates the PSNR values. As can be clearly seen from the table, DWT-SVD based chaotic scheme outperforms [21] and [35]. The improved imperceptibility provided by the scheme is a result of using SVD in the watermarking schemes.

In Experiment 2, the proposed RDWT-SVD based chaotic scheme is compared with the method in [19] to point out the advantage of including chaos in the watermarking. In [19], a non-blind watermarking method that is robust against affine transformations and ordinary image manipulation is presented. The scheme is based on RDWT and SVD.

(c)                           (d)

Fig.2. Watermarked images: (a) Lena (PSNR 93.3193 dB), (b) Peppers (PSNR 91.3384 dB), (c) Baboon (PSNR 57.3595 dB), (d) Airplane (PSNR 49.6457 dB).

In this experiment, gray scale Lena is the host image and the Cameraman is the watermark. Both PSNR and NC values are given in Table 2. The PSNR values obtained by the proposed approach are higher than those obtained by the method in [19] for all attacks. These results prove the imperceptibility and robustness of the proposed algorithm.

Experiment 3 is performed to show the superiority of the proposed method over the well-known algorithms. The NC values under fourteen most common attacks are given in Table 3 for the proposed method. Lena is the cover image and the watermark is the Cameraman image for this experiment. The method is compared with the studies in [18] and [20]. In [18], the image watermarking scheme is based on RDWT and SVD. The authors claim that their scheme achieves a large capacity due to the redundancy in the RDWT domain and at the same time preserves high imperceptibility due to the SVD properties. These statements are also true for our algorithm. Another RDWT-SVD based image watermarking scheme is given in [20] in which the watermark is embedded in all subbands of the cover image. Table 3 shows that the proposed algorithm gives better results than [18] and [20] especially for the LL sub-band. Under Gaussian noise, JPEG (Q = 30), sharpening (80) and Speckle noise (var = 0.01) attacks, our algorithm provides higher NC values for all sub-bands.

In Table 4, imperceptibility of our scheme is compared with four different schemes. The PSNR values without any attack are given in the table. In [8], a hybrid DWT-SVD based image watermarking scheme is investigated. The gray scale watermark is embedded as two parts. The first part is embedded in the LH sub-band and the second part is embedded in the HL sub-band. Finite Radon Transform (FRAT) and SVD based watermarking scheme is given in [36]. There are two schemes in the study. In the first scheme denoted as Rastegar et al. (1) in Table 4, the watermark is embedded in all sub-bands while in the second scheme denoted as Rastegar et al. (2) in Table 4 the watermark is embedded in the LH and HL sub-bands only. The tradeoff between the robustness and transparency is investigated for the schemes. The results given in Table 4 clearly show that the PSNR values obtained with the proposed scheme are higher than those provided by the other methods for all cover images. Additionally, in Fig. 2, watermarked images with PSNR values are illustrated to verify the perceptual invisibility of the proposed scheme.

In Table 5, the proposed algorithm is evaluated under most common image processing and geometric attacks. The NC values are calculated for gray scale Lena, Pepper and Baboon images with the watermark Cameraman. The results are given for all sub-bands. As can be seen from the table, the higher NC values are obtained for the LL sub-band. Also, the proposed algorithm provides consistent responses across all sub-bands. From the results, it is clear that the algorithm is robust against most common image processing and geometric attacks. Furthermore, the LL sub-band is more robust than the other sub-bands against all attacks. The proposed method also ensures the invisibility requirement.

• V.    Conclusion

In this paper, the use of RDWT and SVD together with chaos on image watermarking schemes was investigated. RDWT is shift invariant and it improves the robustness against additive noise because of its redundancy. SVD is a complementary technique for watermarking schemes providing good stability and perceptual invisibility. In the proposed image watermarking scheme, a RDWT-SVD based algorithm is developed by incorporating the chaos to meet the security requirements. PSNR values increase owing to applying chaos to the watermarking scheme. In addition, an improvement on the NC values is ensured. Three experiments were performed to show the effectiveness of the proposed scheme. At the first experiment, the contribution of the SVD was demonstrated. The use of SVD improves the imperceptibility of the scheme. Then, the second experiment was performed to emphasize the advantage of exploiting chaos. The chaotic scheme was compared with the existing methods. The chaos based scheme outperformed the algorithms without chaos. Finally, our algorithm was assessed among the well-known image watermarking methods by performing several simulations in the last experiment. In conclusion, the proposed method was shown to meet the imperceptibility, robustness and security requirements.