Robust Image Watermarking Scheme Using Population-Based Stochastic Optimization Technique

Published Online July 2017 in MECS DOI: 10.5815/ijigsp.2017.07.06

The advancement and widespread use of digital computers along with high-speed networks make digitally formatted multimedia data such as text, image, video, and audio easy to be copied, modified and shared. Malicious attackers can take this as an opportunity and use the technology to misuse the valuable digital resources of others by violating intellectual property right. Hence, the need for effective copyright protecting tools is growing from time to time and become the critical issue for content producers and publishers. Different data securing techniques have been proposed by numerous researchers to address the growing concern. Among these techniques, digital watermarking is one of the most popular ways to solve multimedia data copyright and content authentication problems.

Digital watermarking is a process that embeds a watermark also known as a digital signature within a host multimedia object such that the embedded watermark, which completely characterizes the person who applies it, can be extracted later at the time of dispute to make an assertion about the object. In addition to copyright protection and content authentication, digital watermarking can be used for various applications such as copy control, broadcast monitoring, annotation and content description, ownership identification, tamper detection and covert communication [1, 2].

Digital watermarking techniques can be classified into various categories in numerous ways [3]. Based on the embedding domain, they can be categorized into spatial domain and transform domain watermarking techniques. Spatial domain watermarking techniques embed watermarks into multimedia objects directly modifying selected pixels intensity values. Usually, these techniques are computationally simple and easy to implement [4]. On the other hand, transform domain watermarking techniques insert the watermarks by modifying values of transform coefficients of cover objects [5]. The most common transforming techniques such as Discrete Cosine Transform (DCT), Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT) and Singular Valued Decomposition (SVD) have been used in transform domain watermarking algorithms. Transform domain watermarking techniques provide more robust and imperceptible watermarked data than spatial domain watermarking techniques [6, 7].

Furthermore, depending upon the type of data to be watermarked, the watermarking methods can be classified into four categories: text watermarking, image watermarking, audio watermarking, and video watermarking. However, this paper presents a robust grayscale image watermarking scheme.

Imperceptibility and robustness are the two desired watermarking properties which often use as a criterion to evaluate the effectiveness of watermarking schemes. The term imperceptibility refers to the degree of visual similarity between the original unwatermarked and watermarked images. In fact, watermark inserting process can degrade the quality of host image; however, for an invisible watermarking scheme, the embedding process should maintain the visual quality in acceptable level so that the modification made to host image cannot be noticed easily by an observer. A watermarking scheme is said to be robust if it gives a watermarked document that unauthorized party can not destroy the embedded information without also making the watermarked document useless. The embedded watermark withstands common signal processing attacks and can be extracted or detected even after the attacks.

The rest of this paper is organized as follows. In section II, a brief review of related work is presented. Section III presents feature based reference sub-image forming technique. Detail of SVD is discussed in section IV. Section V illustrates the proposed watermark embedding and extraction procedure. Section VI presents experimental setup and results. Finally, Section VII ends the paper with a conclusion.

• II.    Related Works

Designing robust digital image watermarking schemes, which can embed watermarks without significantly affecting the visual quality of the host images, have become the major challenge in the field of digital watermarking due to the existence of two conflicting watermarking requirements, i.e., robustness and imperceptibility. Researchers across the globe have proposed various watermarking schemes using different techniques, both in spatial and transform domains, aiming to address the problem. They have also employed different optimization techniques, which mimic biological phenomena, to improve the performance of the scheme by searching optimal parameters for watermark embedding.

Because of its unique features, SVD has become the most popular mathematical method for watermark embedding, and numerous robust image watermarking schemes have been proposed using it. A new binary watermark embedding algorithm based on chaotic mixing and SVD for copyright protection application was proposed in [8]. The proposed method embeds a mixed binary watermark into the left orthogonal matrix of the host image. The main limitation of this work is the level of robustness is low for various attacks. Authors in [9] proposed SVD based noble watermarking algorithm which can perform well in both robustness and security for ownership protection applications. They have used a grayscale image, and the algorithm has been tested using six practical conditions, i.e., adding noise, low-pass filtering, JPEG compression, scaling, image cropping, and rotation. However, the method, which they have used to select scaling factor for coefficient modification, will not ensure the trade-off between the robustness and imperceptibility. Using optimization techniques can improve the performance of the algorithm by searching best embedding parameters which can ensure a balance between imperceptibility and robustness. In [10] an evolutionary based digital image watermarking algorithm using SVD technique was proposed. The original image is divided into 8x8 blocks to insert a binary watermark within singular value using quantization method. The performance of proposed algorithm has been improved by employing a genetic algorithm to generate binary watermark. Authors in [11] employed particle swarm optimization (PSO) and wavelet domain technique to propose an intelligent watermarking scheme which can overcome the security problem. The strength of embedding watermark in different blocks is controlled by invoking a PSO method to resolve the conflict between imperceptibility and robustness. But, it is also worthy to take into consideration that both imperceptibility and robustness highly depend on the methods employed to select regions or blocks of the images for watermark embedding. In recent years, feature-based image watermarking schemes that embed desired watermark into selected regions with features like edge, texture or fractal dimension, have been introduced. Selecting different regions of the image with different features may depend on the watermarking applications and directly influences the level of robustness and imperceptibility of the scheme. In [12] a robust image watermarking algorithm, which can resist both geometric distortion and signal processing attacks, was proposed using a feature extraction method called Mexican Hat wavelet scale interaction. The authors have used the extracted feature as reference points for both watermark embedding and detection. Authors in [13] proposed a robust, featurebased image watermarking scheme using discrete wavelet transform and singular value decomposition techniques. The PSO algorithm offers a systematic way to consider the improvements of the scaling factor that controls the strength of the embedded watermark.

Even though several image watermarking algorithms for different application have been proposed so far, conducting further research in the field is still required to fill existing gaps. In this paper, an optimized grayscale image watermarking scheme using block based SVD, edge detection and PSO technique is proposed. Since human eyes are less sensitive to changes take place in regions of the image having more number of edge or texture, embedding watermark in these regions may not degrade the quality significantly. Hence, in our work Canny edge detector is employed to select blocks with large number of edge pixels to embed a binary watermark. The particle swarm optimization (PSO) algorithm is employed to search appropriate scaling factors which determine the embedding strength of a watermark.

• III.    Feature-Based Reference Image Formation

Feature-based digital image watermarking techniques have become the most popular strategy to design robust and imperceptible watermarking scheme. The existence of various feature detection techniques enables designers to select different regions or blocks of an image for watermark embedding. Various feature detectors extract local feature by performing specific transformations on images. In digital watermarking, regions or blocks having desired features can be used as a reference point for both watermark embedding and extraction. In this work, we have used the canny edge detector for selecting image blocks to embed a binary watermark. Even though there are number of edge detecting techniques, we have preferred canny edge detector due to its superior performance over the others. First, original image IG of size MxN is partitioned into non-overlapping blocks Bk of size mxn. Then, edges are extracted from each block using canny detector, and total number edge pixels in the block ( NE) are computed using the following equations.

E k = edge ( B k ), fork = 1,2,..., П ь        (1)

N k -ell; , E k (и)        (2)

where, edge (.) represents the edge detection operation, nb is the total number of blocks, Ek(i,j)=1 for edge pixels and 0 otherwise. The blocks are reordered based on the number of edges keeping their position as a key (Qk) to use it later. To embed watermark of size pxq, a total of Nt (where, Nt=pq) numbers of blocks are required and the first reference image IH is formed by merging these blocks together. The same numbers of blocks with the least number of edge pixels are also selected to form the second reference image IL, which uses as a reference image for watermark embedding and extraction.

N

/ /. ip-ч) = U_A ' ₌₁( B ) H

N tL (p,q)=U* 1 /B) L

Where, U(.) represents blocks merging operation, B ^ and B ^ are blocks with large and small number of edges respectively. In Fig. 1 the overall steps involved in the reference image formation are depicted well.

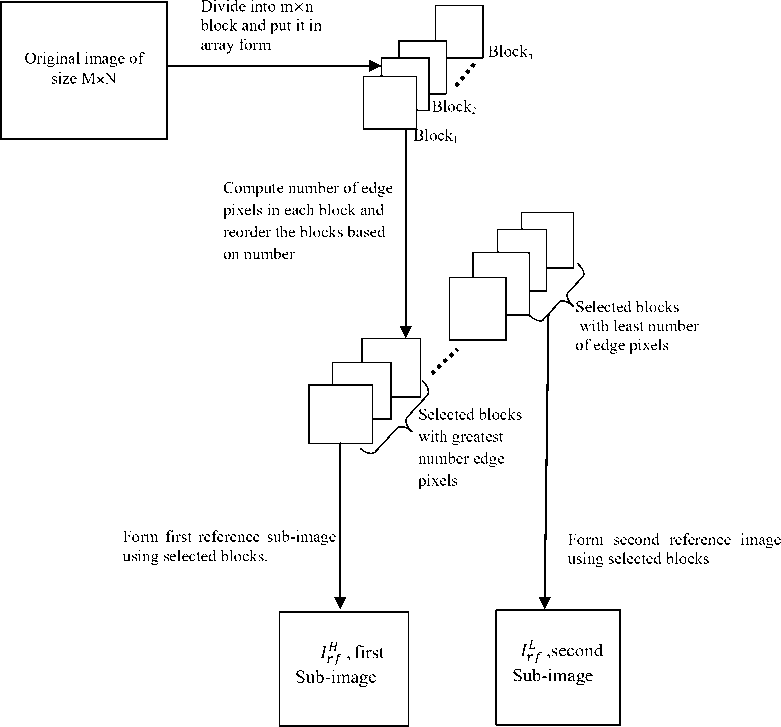
Fig.1. Flow chart for reference sub-images formation.

• IV.    Singular Value Decomposition

Singular value decomposition is linear algebra technique, which uses to factorize a real or complex rectangular matrix into three unique matrices. If Y is a real M-by-N matrix, then there exist two orthogonal matrices U and V (i.e., UUT=I, VVT=I) and one rectangular diagonal matrix S, such that

Y = USVT = " u 11    ■ u 21    . u 1M u2M r»11 0 : 0 s22 0 > r V11    ■ v 21    • -  v 1N v2M T (5) X uM 1 UMM J X 0 0 sMN J X vN 1   • • 1   vNNJ where matrix S is a nonnegative diagonal matrix containing the square roots of the eigenvalues of either U or V arranged in descending order diagonally (i.e., s11 > s22 > s33 > • • > sMN). SVD has great application in the field of image processing, especially in digital image watermarking. The followings are some of the advantages that we can get from SVD when we use it in a watermarking algorithm.

• i.    Image quality is not affected significantly due to a slight modification of singular values during watermark embedding process.

• ii.    Singular values have good stability and their values are rotationally invariant.

• iii.    SVD can pack large energy signal within few coefficients.

In this paper, we have used SVD to factorize the subimages to embed a binary watermark.

• V. Proposed Scheme

Using multiple scaling factors (MSF) other than a single scaling factor (SSF) to modulate different ranges of selected coefficients during watermark embedding process can significantly improve the performance of the scheme. In this work, block based SVD is performed on reference sub-images ( 1^ and 1^ ) to obtain the respective singular value coefficients ( S^(pq) and S^pq) ). Then the difference (D(p,q)) between Spf(p q) and S^(p q) is computed using the following equation:

D ( p , q ) = \S« ( „,„ ) ( i , j ) - S ^f ( _p,_q ) ( i , j )        (6)

where i=j=1 and (p,q) refer to block indices. D (p,q) values are again divided into n number of non-overlapping sub ranges (r k ) so that multiple scaling factors (β k ) can be used to embed a watermark based on the magnitude of D (p,q) .

^D max = max ^{D (} p , q))

^D min = min ^{( D (} p , q))

d = (D -D Mn max      min rk = [(k — 1)d, (kd)), fork = 1,2,

Therefore, for the completion of embedding process n numbers of scaling factors are required, and in this paper, we have used five scaling factors (βk), where k=1, 2… 5 such that βk > βk+1. After obtaining each sub-range interval, a singular value coefficient that belongs to a particular sub-range are modified by a corresponding scaling factor depending on watermark bits as per equation (8).

i^f W b ⁽p, q) = ¹

H rfW ( p , q )

'^SH ( p , q ) (i,j) ,                         ^{f S} H ( p , q ) (i,j)

_ S HH ( p , q ) (i,j) + ^L ( p , q ) (i,j), if S ^ ( p , q >6 j) if W b (p,q) = 0

> S rL ( p , q ) (i,j) ^ S rL ( p , q ) (i,j)

'^SH ( p , q ) (i,j) ,

_ 8^,(p,q)(i,j) — PS^f (p,q)(i,j), f SH(p,q)(i,j) < SL(p,q)(i,j)

^{f S} H ( p , q ) (i,j) ^ ^S L ( p , q ) (i,j)

where scaling factor β=β k if D (p,q) is in the range r k and i=j=1.

• A.    Watermark Embedding Technique

Watermark embedding algorithm takes original host image IG and binary watermark Wb of sizes MxN and pxq respectively as input and provide watermarked image Iw as an output. The followings are the steps for the proposed watermark embedding algorithm.

Step1 : Original host image I G is decomposed into two references sub-images 1 ^ and 1^ using the procedure discussed in section III.

Step2 : Perform block based SVD operation on

If and iff

[ U r/ ( p , q ) , ^S rf ( p , q ) , ^V rf ( p , q ) ^] = ^{SVD ( 1} rf ( p , q ) )

^{[ U} rf ( p , q ) , ^S rf ( p , q ) , ^V rf ( p , q ) ^] = ^{SVD ( 1} rf ( p , q ) )

Step3 : Embed binary watermark W b (p,q) by modifying S ff(_{p 9}) based on the value of the watermark bits as per equation (8) and use PSO based procedure to find best scaling factors ф_к) for each sub-range.

Step4 : Apply inverse SVD operation to obtain watermarked blocks B HH .

H       H     H      HT

B W ⁽ p . q )     ^Urf ⁽ p . q ) S ^rfW ⁽ p . q ) V ^{rf (} p . q )

Step5 : Place each block to their original position using key Q_k to obtain watermarked image I_w.

• B.    Watermark Extraction Technique

Possibly an attacked watermarked image I W and key (Q k ) are required as inputs for the extraction process. The steps for watermark extraction are given as follows.

Step1 : Decompose possibly attacked watermarked image into two sub-images (i rf_w and i rfw) using key and procedure discussed in section III.

Steps2 : Apply block based SVD on i Pf_w and I rf_W .

H *      H *       H *               H *

U* ( p , q ) , S w ( p , q ) , V ( p , q ) ^]= SVD ⁽ I rfw ( p , q ) )

L *        L *         L *                   L

[ U w ( p , q ) , ^S w ( p , q ) , V w ( p , q ) ^]= ^SV D ⁽ I rfwo , q ) ) J

Steps3 : Extract the watermark using the rule given in equation (12).

W_E ( p , q )

1,

0,

ifS f/;_p , q ) (i, j) >  S W * p , q ) (i, j)

otherwise.

where i=j=1 and (p,q) represent block indices.

• C.    PSO Based Parameter Optimization

Scaling factors, which are used to modify the selected coefficients during watermark embedding, significantly affect the performance of the watermarking scheme. Therefore, the problem of finding suitable scaling factors which can give optimum performance in terms of visual quality and robustness can be viewed as an optimization problem. The optimization problem can be formulated as follows:

Maximize R ([в к ]).

Maintaining T ([вк]) ^Tth- where R(.) and T(.) are robustness and imperceptibility achieved using the scaling factors вк respectively, and Tth is user defining quality threshold value. Fitness function

(FF), through which the optimization problem is guided toward optimum performance, should be formulated properly putting these watermarking objectives into consideration.

In this paper, population based stochastic optimization technique PSO is employed to find a solution to the problem. The algorithm was first developed by Eberhart and Kennedy in 1995 [14]. Randomly generating a swarm of particles from search space having initial position xi(t) and velocity vi(t) is the first step in a PSO algorithm. The quality of each particle is evaluated using formulated fitness function.

FF = T ( в к ) + у ^ " R i (в к )          ⁽ 13)

Where R_i is robustness measured against i^th attack, T is quality achieved, and N is the total number of attacks performed. у is a weighting factor for R i .

Based on the fitness value, each particle personal best (P best ) and overall global best (g best ) are determined. Unless predefined stopping conditions are satisfied, the particles keep on moving around the searching space looking for optimum values and update their velocity and position in every hop using equation (14) and (15) respectively.

V ⁽ t + 1) = Wv i ⁽ t ) + C i rand ⁽ p bes, ^- X ⁽ t )) + C 2 ^raⁿd ⁽ g bes₍ ^- x i ⁽ t )) ⁽¹⁴⁾

X i ( t + 1) = X i ( t ) + V i ( t + 1)                     ⁽¹⁵⁾

where W is inertia weight which determines the step size, C₁ and C₂ are learning factors which determine the effectiveness of local and global learning. The term rand refers to an operation which randomly generates numbers between 0 and 1. In Fig.2 the flow chart of PSO algorithm is shown .

We have used the metric peak signal to noise ratio (PSNR) and bit correct rate (BCR) to measure the level of imperceptibility and robustness respectively, and their definition is given in section VI. The overall steps for PSO based parameter optimization are summarized and given as follows:

• i.    Set suitable initial values for parameters (i.e., initialize particles).

• ii.    Use the parameters and embed a binary watermark into host image following the procedure which is given in subsection A.

• iii.    Perform different attacks on watermarked image.

• iv.    Extract watermark from attacked image using the procedure given in sub-section B.

• v.    Compute fitness value and obtain p_best and g_best.

• vi.    Compute next velocity and position of each particle using equation (13) and (14).

vii. Update current p best , g best, velocity and position.

viii. Repeat step ii to vii until stopping conditions are satisfied.

Finally, use obtained optimum parameters (/? _fc ) and embed a watermark

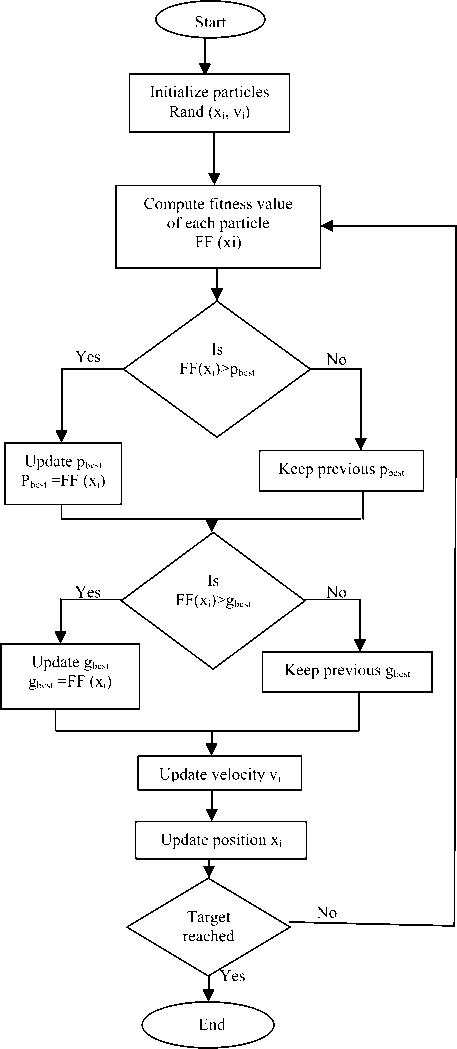
Fig.2. Flow chart for PSO algorithm.

VI. Proposed Scheme

In this section, the performance of the proposed scheme is evaluated through simulation using eight standard grayscale images of size 512x512 as host image. A logo of copyright of size 32x32 is used as a watermark image. The host images and the watermark logo are shown in Fig. 3.

The watermark is embedded into the host images using proposed algorithm, and the level of quality distortion caused due to watermark insertion is evaluated using a PSNR metric. For watermarked image I w and host image I G of size MxN, the PSNR is computed by comparing the two images as follows.

PSNR = 10log

YmN Z i = 1 Z j = 1 ( I w ⁽ i , j )   I G ⁽ i , j ))

dB

The watermarked images are shown in fig. 4, and the corresponding PSNR values, which show the quality achieved, are presented in Table 1.

The visual quality of watermarked images in fig. 4 and the PSNR values in Table 1 confirm that the proposed watermarking algorithm can achieve higher imperceptibility. When good imperceptibility achieved, watermarked image appears nearly identical to the original host image and has high PSNR value. Generally, imperceptibility within 38 dB is the minimum accepted value of PSNR [15].

(b)

(c)

(e)

(f)

(g)

(h)

(i)

Fig.3. The host images and the watermark logo: (a) Baboon, (b) Pirate, (c) Lena, (d) peppers, (e) living room, (f) Zelda, (g) Elaine, (h) Bridge, (i) watermark logo

(a)

(b)

(c)

(e)

(f)

(g)

(h)

Fig.4. Watermarked images: (a) Baboon, (b) Pirate, (c) Lena, (d) peppers, (e) living room, (f) Zelda, (g) Elaine, (h) Bridge

Table 1. The quality that can be achieved, for each host image, in terms of PSNR (dB).

Host Images	Baboon	Pirate	Lena	Peppers	Living room	Zelda	Elaine	Bridge
Quality in PSNR (dB)	44.2586	44.4857	47.4493	43.7711	44.1419	44.2342	43.2457	43.1219

For the sake of convenience, in the later sections, the attacks are identified as GN, SPN, MF, HE, GC, CRP, JPEG-C, AVF, G-LPF, CM, BP, SRP, RS, and WF respectively. In fig. 5 and fig. 6 attacked watermarked Lena images are shown.

The presence of the embedded watermark withstanding applied attacks is verified by extracting the watermark from the attacked image using the proposed extracting procedure.

(a)

(e)

Fig. 6.Attacked watermarked Lena image: (i) Wiener filter, (j) Image sharpening, (k) Average filter, (l) Bit plane replacement.

Bit Correct Rate (BCR) is employed to compute the degree of similarity between the original and extracted watermark images. For original watermark Wb(i,j) and extracted watermark WE(i,j), the robustness metric BCR can be computed using the following equation.

2 ’ , = 1 2L W . ( i , j ) ® W E ( i , j ) BCR =------------------

where ® and (.) are binary Xor and Not operator respectively. In fig. 7, extracted watermark images from attacked watermarked Lena and Baboon images are shown. The obtained result illustrate that the proposed method can give good quality extracted watermark image against the all attacks performed except rotation attack. Table 2 shows the BCR values between the original watermark and extracted watermark after the attacks.

pq

Attacks	Extracted watermarks form		Attacks	Extracted watermarks form
	Lena	Baboon		Lena	Baboon
No attack (NoA)	©	©	JPEG compression attack QF=65% (JPEG-C)	©	©
Gaussian noise attack (GN)	©	©	Average filter (AVF)	©
Salt & pepper noise attack (SPN)	©	©	Gaussian filter (G-LPF)	©	©
Median filtering attack (MF)	©	©	Camera motion (CM)	©	©
Histogram   Equalization   attack (HE)	©	©	Bit plane removing (BP)	©	©

Contrast adjusting attack (CA)	©	©	Image sharpening (SRP)	©	©
Cropping attack (CRP)	©	©	Resizing (RS)	©	©
Rotation attack 0.50 (RT)			Wiener filter (WF)	©	©

Fig.7. Extracted watermark images from the attacked watermarked Lena and Baboon images.

When BCR value of extracted watermark is close to 1 under applicable attacks, then the watermarking scheme is said to be robust against these attacks. From Table 2, it can be observed that the maximum BCR value obtained is 1 and a minimum value is 0.5104 which is for rotation attack. Hence, the obtained results highlight the performance of the proposed methods under different attacks. Except for rotation attack, the proposed scheme shows the highest robustness against all other attacks performed. The corresponding optimized multiple scaling factors, which provide the best PSNR and BCR values for Lena, Baboon, and Bridge host images, are presented in Table 3. These are obtained from PSO based watermarking scheme. In order to evaluate the performance level of the proposed method, we have compared our results with other existing methods, which are reported in [16-18] and is shown in Table 4. The BCR results, which are given in the Table 4, are obtained by calculating the average BCR over the eight host images. It can be seen from the result that the proposed scheme outperformed previous schemes in terms of imperceptibility and robustness. However, the robustness against JPEG compression for QF below 60% and cropping attack is slightly lower than that of J. Das, et. Al. and J. Wang, et al. respectively. In fact, Higher robustness could come at the expense of some degradation in quality due to the conflict between them.

Table 2. BCR between original watermark and extracted watermark under different attacks.

Attacks	Watermarked images
	Lena	Baboon	Pirate	Peppers	Living room	Zelda	Elaine	Bridge
NoA	1	1	1	1	1	1	1	1
GN (µ=0, v=0.001)	0.9936	0.9959	0.9851	0.9816	0.9871	0.9735	0.9870	0.9796
SPN (D=0.002)	0.9851	0.9991	0.9766	0.9594	0.9647	0.9583	0.9506	0.9741
MF (3x3)	0.9836	0.9983	0.9712	0.9545	0.9562	0.9372	0.9658	0.9517
HE	0.9872	0.9975	0.9851	0.9578	0.9742	0.9709	0.9718	0.9712
GC (γ=0.925)	0.9751	0.9915	0.9808	0.9739	0.9658	0.9517	0.9704	0.9867
CRP (25%)	0.9715	0.9987	0.9829	0.9546	0.9742	0.9796	0.9615	0.9684
RT (0.50)	0.7137	0.7345	0.7971	0.7566	0.6278	0.5774	0.5483	0.5104
JPEG-C(QF=65%)	0.9871	0.9809	0.9808	0.9807	0.9729	0.9673	0.9852	0.9824
AVF (3x3)	0.9521	0.9451	0.9396	0.9377	0.9419	0.9218	0.9417	0.9349
G-LPF (3x3)	0.9936	1	0.9845	0.9879	0.9860	0.9787	0.9896	0.9843
CM (len=9,θ=0)	0.9942	0.9964	0.9766	0.9882	0.9773	0.9603	0.9637	0.9862
BPR(LSB removed)	0.9945	0.9954	0.9845	0.9867	0.9909	0.9902	0.9934	0.9693
SRP	0.9882	0.9845	0.9766	0.9847	0.9878	0.9852	0.9819	0.9793
RS (50%)	0.9766	0.9998	0.9826	0.9853	0.9698	0.9533	0.9863	0.9818
WF (3x3)	0.9875	0.9893	0.9829	0.9856	0.9524	0.9581	0.9813	0.9732

Table 3. Optimized multiple scaling factors (MSF) obtained from PSO.

Cover image	PSNR	BCR (JPEG, QF=10)	Optimized Scaling factors(βk) for different ranges
			β 1	β 2	β 3	β 4	β 5
Lena	47.4493	0.6521	0.0163	0.0676	0.0721	0.0930	0.1018
Baboon	44.2586	0.6491	0.0297	0.0560	0.0693	0.0810	0.0983
Bridge	43.5219	0.6573	0.0527	0.0556	0.0646	0.0924	0.0932

Table 4. Proposed method robustness comparison with other three methods in terms of BCR.

Attacks	Attack level		Other proposed methods			Proposed method
			(J. Wang, et al.) [16]	(Das, et al.) [17]	(M. Abdelhakim, et al.) [18]
SPN	D	0.01	0.927	0.914	0.899	0.931
		0.05	0.792	0.653	0.681	0.803
MF	Window size     (3x3)		0.698	0.915	0.917	0.964
	(5x5)		0.588	0.781	0.796	0.863
HE			0.981	0.902	0.984	0.986
GC	Gamma          0.9		0.998	0.946	0.989	0.994
CRP	Upper left quad.		0.687	0.983	0.995	0.987
	Upper right quad.		0.675	0.988	0.993	0.973
	Lower left quad.		0.996	0.992	0.986	0.994
	Lower right quad.		0.995	0.978	0.984	0.991
RT	Degree              0.50		0.510	0.585	0.580	0.658
JPEG-C	QF	15%	0.620	0.677	0.555	0.757
		20%	0.670	0.787	0.637	0.791
		25%	0.69	0.887	0.725	0.842
		30%	0.719	0.951	0.819	0.911
		35%	0.747	0.974	0.887	0.929
		40%	0.772	0.997	0.925	0.935
		50%	0.815	0.999	0.970	0.967
		60%	0.851	0.999	0.983	0.979
		70%	0.892	0.999	0.998	0.999
		80%	0.936	0.999	0.999	1
		90%	0.973	0.999	0.999	1
AVF	Window size     (3x3)		0.644	0.921	0.940	0.949
	(5x5)		0.550	0.762	0.791	0.815
G-LPF	Window size     (3x3)		0.997	0.995	0.999	0.999
	(4x4)		0.817	0.896	0.988	0.993
IS			0.984	0.944	0.967	0.985
RS	Scale ratio       (50%)		0.991	0.820	0.989	0.992

From the overall results presented in this section, we can observe that the new proposed watermarking technique is capable of achieving higher imperceptibility and robustness against both image processing and geometric attacks and is considerably more robust than other three compared methods.

• VII. Conclusion

The challenge of designing both robust and imperceptible image watermarking schemes for multimedia copyright protection application gets a solution in this paper, and a new robust image watermarking scheme based on edge detection, SVD and PSO technique that can satisfy the watermarking requirements is presented. To improve the quality of watermarked image the watermark is embedded in selected blocks of the image having large number of edges. Optimized multiple scaling factors are used to modify different range of singular values during watermark embedding process. Different attacks have been performed on watermarked images to evaluate the level of robustness, and the results obtained from the simulation shows that proposed method provides best BCR values for the attacks performed. Three other watermarking techniques have been considered for comparison and the proposed method achieves significantly improved robustness and imperceptibility compared to others.