Robust Reliable Control for a class of Uncertain Switched Linear Systems

Published Online March 2011 in MECS

Switched system is a special class of hybrid dynamical system, and it is composed of a number of subsystems, either continuous-time or discrete-time system, and a switching law, which defines a specific subsystem being activated during a certain time. Switched systems have widespread applications in control of mechanical systems, automotive industry, air traffic control and many other fields. Therefore, in the last 20 years, analysis and synthesis of switched systems have attracted the interest of many scientists [1~ 6]. Stability is of great importance in the switched system and in the past 20 years, people have witnessed considerable effort and significant contributions concerning this matter. A series of methods and conditions based on common quadratic Lyapunov functions (CQLF) and multiple Lyapunov functions approach have been given. For example, in [7], state feedback controllers based on multiple Lyapunov functions technique are designed for each subsystem to robustly stabilize the closed-loop of switched delay system and to ensure a prescribed performance on attenuation of all admissible parameter uncertainties, respectively. In [8], robust stabilization for a class of switched systems which the uncertainty does not satisfy so-called matching condition is considered. Based on common Lyapunov functions technique, a kind of robust controller of state feedback and a kind of robust controller of output feedback are constructed to make the closed-loop system be asymptotically converging to the equilibrium point under arbitrary switching strategy.

Currently, many industrial systems usually consist of many components such as actuators, sensors, computers and communication networks. For environment or other factors influence systems, actuators failures often occur in applications. Actuators are very important in transforming the controller output to the plant. Therefore, any abnormality in one of these actuators may drastically change the systems behavior, resulting in performance degradation, instability, or even total breakdown. In order to maintain the system reliability and safety, it seems necessary to design a reliable control system which can tolerate failures of actuators, while maintaining an acceptable level of the closed-loop system stability and performance. In recent years, the problem of reliable control for switched systems has attracted much attention, and a series of design methods have been given [9,10,11]. For example, in [9], a method based on dwell-time is used to design reliable controller for switched linear systems, in [10], multiple Lyapunov functions approach of designing reliable controller is developed to stabilize the switched nonlinear systems. By these design methods, systems all achieve satisfactory stability. On the other hand, over the past few decades, the H∞ control problem for uncertain systems with disturbance input has been an active topic in control system theory and application. For example, in [12], LMI optimization approach is used to design the reliable control for uncertain nonlinear system, and the reliable control designed guarantee global exponential stabilization. In [13], the problem of H∞ robust control for a class of discrete time switched systems with parametric uncertainty is investigated under arbitrary switching, and state feedback controller is designed for the switched systems using common Lyapunov technique, and the controllers guarantee the closed-loop systems are robust stable with H∞ disturbance attenuation. However, to the best of our knowledge, the issue of reliable Hда control for switched linear systems with external disturbances has not been fully investigated and remains many problems.

In this paper, we investigate robust reliable H _да control for uncertain switched linear systems with external disturbances and also with unknown time-varying norm-bounded parameter uncertainties in the state matrix and output matrix. Based on LMI method and convex combination technique, a sufficient condition for the switched linear systems with external disturbances to be quadratically stable is derived for all admissible actuator failures, and the corresponding switching law is designed.

The rest of this paper is organized as follows. In section 2, we present the preliminary knowledge for switched systems together with reliable control problem formulation. In section 3, an approach for design robust reliable H да controller is proposed in a straightforward way. In section 4 a numerical example is given to illustrate the design methods proposed in this paper, followed by some concluding remarks in Section 5.

as Q i c { 1,2,L, n i } ( i e M ) , and is possible to fail. The other set of actuators which are robust to failures and essential to stabilize a given system, is denoted by Q i c { 1,2,L, n i } -Q i ( i e M ) . Introduce the decomposition B i = B Q i + B q i ( i e M ) , where B _Q i and B q i are generated by zeroing out the columns corresponding to Q i and Q i respectively. Let m i c Q i correspond to an actual subset of the actuator failures, and introduce the decomposition B i = B _; + B _; ( i e M ) , where B _; and

B . are formed from B i by zeroing out the columns

corresponding to . and ® i respectively. So, we have

the following inequalities holds

B q . B Q i = B^B . + B q i - t X i -.i

B q i B Q i = B^ - B q i -X i -.

So, we have

II.  P ROBLEM F ORMULATION

^BB Q i <  BX

Consider the following uncertain switched linear systems:

x ( t ) = ( A _a + A A _a ) x ( t ) + B . w c ( t ) + B _a u _a ( t )

; z ( t ) = ( Cc +A Cc ) x ( t )

y( t ) = C7x ( t )

. x (to) = xо

In this paper, the purpose of our control for the switched systems (1) is stated as follows:

Let a constant у >  0 be given. For switched system (1)

where : x ( t ) e R" is the state vector, w _c ( t ) e L 2 [ 0 , да ) is the disturbance input vector, u _c ( t ) e R k is the control input vector, z ( t ) e R q is the controlled output, c : R ₊ ^ M = { 1,2,K, m } is the right continuous piecewise constant switching signal to be designed. A i B i B_t ,C 1 1 are constant real-valued matrices with appropriate dimensions, A A i and A C i are uncertain real-valued matrix functions, and are of the following form

[ A A i A C ] = H i B i C t ) [ E _a E , 2 ] , В T ( t ) B i ( t ) <  I (2) where H_i , E_{i 1}, E_{i 2} are constant matrices with suitable dimensions, B i ( t ) is an uncertain matrix.

A switching sequence is expressed by

X = { x o ; ( i o , t о ) , ( i i ,t i ) ,L , ( i j , t j ) ,L ,| t j e M , j e N } where t ₀ is the initial time, x ₀ is the initial state, when t j <  t <  t j _{+ 1} , the i j . -th subsystem is activated. Therefore, when t e[ t j ., t j .₊₁ ) , the trajectory of the switched system (1) is produced by the i_j -th subsystem ^[2]. We now consider the reliability with respect to actuator failures which are restricted to occur within the i -th subsystem. Actuators can be classified into two sets. The set of actuators which are susceptible to faults is denoted

with any admissible parameter uncertainty and also with actuator failures corresponding to any m i c Q i , design reliable feed-back controller for all subsystems and a switching law such that the closed-loop system of system (1) is quadratically stable when w i = 0 and the output z satisfies || z ||2 <  y|| w i ||₂ under the zero initial condition.

Lemma 1 ^[14] For matrices of appropriate dimension, and ^ >  0 , we have X^TY + Y^TX <  ^ X^TX + ^^x Y T Y

Lemma 2 ^[15] For given matrices U , V , W and X of appropriate dimension with X satisfying X = X^T ,

X + UVW + W^TV^TU^T <  0

holds for all V satisfying V^TV <  I , if and only if there exists a scalar £ >  0 such that

X + £UUT + £-1WTW < 0.

Lemma 3 ^[12] (Schur complement). For a given matrix

S =

^S 11

_{S 1} T ₂

^S 12

^S 22

with S 11 = S 1 T

T

22 ⁼ 22

then the

following conditions are equivalent:

1) S < 0

2) S 11 <  0 , S 22

3) S 22 <  0 , S 11

- V T V-1 v

12 22 12

— S'   S'^-1 s* ^T

^S 12 ^S 22 ^S 12

< 0

< 0

Definition If there exists a positive definite symmetric matrix P , a positive constant и and switching law such that for any admissible uncertainty and actuator failures the derivative of Lyapunov function satisfies jV ( x ( t ) )

<- U|x ||² , then system (1) is said to be quadratically stable with actuator failures.

III. M AIN R ESULTS

In this section, we will present one method for designing reliable H „ controller and switching law to ensure that closed-loop system (1) will be quadratically stable with actuator failures and an H да norm bound у .

Theorem 1 For system (1), if there exist positive scalars Pi, ai, 2i,si, у and a symmetric positive definite

N

< 0

W

matrix P , such that sHH -1 < 0           (4)

" A p+pA + r

_    NT where

A = X в [ A - a . B q B^M - ] i = 1                                i i

m

X Д = 1

i = 1

R = X Pi [s.-1 EEn + a-M.Bq BM + 2ETE^ ]

i = 1                                                 ^{i i}

N = [ PH 1 L PH m PB L PB m C T L C - ]

W = diag { - n 1 ,L , -rm I , - ^ I ,L , -p _mI , P^S H , H T - 1 ),

L, PmAS m H m H T - 1 ) }

n = Д 12,

^ = в,-'у2

M_i is any appropriate dimensions matrix. Then there exist feedback controller u i = k i x and a switching law c : R ₊ ^ M = { 1,2, K , m } such that the closed-loop system of system (1) for all admissible actuator failures is quadratically stable and the controlled output z satisfies II z\ 12 <  Y l H |₂. Control gain k i = - 0.5 a i B^TP .

Proof By the Schur complement, inequality (4), (5) are equivalent to X Д -N i <  0 , i = 1

where

N = (a - a^ bT mT f p+pU - a^ bt m )+

• -           -        - Q i Q i -I                      -        - Q i Q i -I

= 1

Д >  0, there is certainly an i e M such that x^T N ii x <  0 .

и Qi = Rn \ {0}, Qi I Qj = ф,i * j

Design switching lawi = c (x(t)), when x(t) e Qi,i e M . Suppose that the output of failed actuators is zero, then by considering the design controller, we have ui (t) = kix (t), ki = -0.5aiBTi P.                    (6)

We define the Lyapunov function as V ( x ( t ) ) = x ( t ) ^T Px ( t ) . When h = 0 and x ( t ) e Q, , along the trajectories of system (1), the time derivative of V ( x ( t ) ) with (3) and (6) is given by

• V ( x ) = x^T ( A ⁺ A A ) ^{T px +} ( ^B ^i. u i ) ^{T px + xTp}B_6)i u_t ⁺

x^Tp ( A ^+A A ) ^x

= x^T [ AP + PA - a pB ^ B l P + E T E, ^r( t ) H T P ] x

+ x^T PH »,.(t ) E 1 x

• <    x^T [ AP + PA - a i PB q B Q p + E T E ( t ) H T P ] x

+ x^T PH »,.(t ) E 1 x .

Form lemma 1, (2), switching law and an any given matrixM with appropriate dimensions, we have jV (x )< xT

( a - a B^ b t m T )^t p + a MB b t m T \ ¹ i q - q - i 1             i i Q i Q i i

+p (A - aiBq BTmT )+2-1 PHHTp+2ETe,1 ] x

• <    -xT [y-2PAiATp + aiMiBQ BQ^MT + s,-1 eTe,2

+ C , 1 ^t ( I - S - H i H - ) ^{- 1} C , 1 ] x

• <    - x^T V i x .

Obviously,

• V - = у ~² PB - B - P + C - , ^T ( I - s - H - H T ) C - , + a - M - B qB Q. M T + s;‘ E -2 E -2

is positive definite matrix, then there must exist some positive constant и such that V ( x ) < - Щ x ||² holds. It follows from definition that the closed-loop system of system (1) is quadratically stable with actuator failures.

Now, we proof the problem of H „ performance. Firstly, we suppose the zero initial condition and h e L ₂ [ 0, да ) . Secondly, according to the switching sequence and switching law, we assume that the first subsystem is activates at the initial time. Then we have

Let Q i = { x | x^T N i x <  0, V i e M } , then vQ. = R n \ { 0 } .

Construct the sets

Q1 = Q1,L , Qi = Qi - iu1 Qj ,L , Qm = Qm - mu-1 Qj

Obviously, there exists

J = Jo” ( z T z ^- Y 2 w T wi^dt

= J^ ” L ( z T z - y ² w^Tw_t ) + V&(x ) J dt - x ( ” ) T Px ( да )

< I IJt ' [(zTz - Y2wT w) + V(x)]dt i=1 j=1 tj L v                         /             _|

m ”

= 11J ?^{+1 [} z z - Y w > w + x ( A P + PA ) x = 1 j = 1 ^j

+ x T ( A A T P + P A A ) x + x T PB^kx + ( B ^ kx ) T Px

+ x^TPB _;w + w^T Bi T Px J dt .

By lemma 1, (2), we obtain

J <  II IJ^^{+ 1 [} z T z ^- Y ² w¹w ^{+ x} T ( A ⁺ B ^ k i ) T ^Px

= 1 j = 1 jj L

+ x^TP (A + B. k) x + x k PH HI Px + x T & E l En x

Ш.                       it            It                             1 1

+ x^TPB _tw + w T B T Px J dt

such that S i HHI - 1 <  0 holds, then from the Schur complement and lemma 2, (8) is equivalent to

(a - aB_a b I mII p + p ( A - a-Bfi b T mI )

X ^{t           t} Ь к Ь 2.^ t 1                     X ^{t           t} ii t Ь 2! ^t 1

+ ^,⁴ ETE_n + aMBn b T m T + k^-1 ph Hl p        (9)

t 1 2 t 2 t t ^^t' ^^t t "'t              t t                                       x '

- 1

+ k E T E _a + y -2 PB t B T P - Ck ( s H H T - 1 ) C <  0 which can be deduced to get J <  0 .That is to say, (9) is the sufficient condition to ensure H ” the norm bound constraints    ||z ||2 <  Y|w |₂ ■ This completes the proof.

In the Theorem 1, we assume that the output of failed actuators is zero. However, generally speaking, the output of failed actuators may be arbitrary signal. Here we suppose that the output of failed actuators belong to L 2 [ 0 , ” ) , and let the output of faulty actuators is

= 1 1 f J i -⁺¹ x^T [ ( A + В ш k t ) T P + P ( A + В ш k t ) + k t E T E t 1 ■ k PH H P + C T C + Y 2 PB B T P J xdt

T m ” -1;.л

-I IJI+1 (Y1BTPx - Yw) (y1BTPx - Yw) dt i=1 j=1 1j x                           7 x                           7

I J t j -⁺¹ x ^T [ ( A + В ш k t ) T P + P ( A + В ш k )

+^ E T E 1 + k PH HP + C T C + Y - ² PB Bp J xdt

From (3), (6) and any given matrix M with appropriate dimensions we obtain

m ” ,t.

j ;^{j + 1} x T i = 1 j = 1 ^tj

(A - a Bn B T Ml) T P + k ^- PH HI P у ^t I 2" ь . I 1             .i          I ^t

denoted by u T and regarded as another disturbance input besides w t ( t ) . Defining w F ( t ) = [ w ¹ u T. ] , the system (1) can be expressed as

' x ( t ) = ( A_a + AA „ ) x ( t ) + [ H t B „_ J w F ( t ) + B₅u „ ( t )

_Л ( t ) = ( C_o +A C_o ) x ( t )                                 (10)

У ⁽ t ) = C%" A x ⁽ t )

„ x ⁽ t 0 ) = x 0

From a similar proof in Theorem 1, we obtain the following theorem.

Theorem 2 For system (10), if there exist positive scalars Д -, a , k , S , Y and a symmetric positive definite matrix Q , such that

+aMB B T mI + p (a - ав_й bT mT ) + C' T C t t Д2' Д2' t                  t         t ^ t' ^ t t              t t

+Y-2 pBB tBiT P + kET Ea J xdt, where

C^ i = C t + A C^

Obviously, J <  0 is equivalent to

(a - aB^ b I mII p + p ( A - aB^ b T mI )

\ t t ^ t' ^ t' t J                  \ t t ^ t' ^ t' t I

+k E l E_n + a MBnB l Ml + k ^- phhIp + <^ T C ^i    (7)

-'ll 1 1 1          t t ь 2-i ь 2-i t 11            I I               I t              x '

g J A T + J AQ + R

N ^T

/X

N G

W  0 <  0

G ^T      0 L

+ Y PB B T P <  0.

By (2) and the Schur complement, (7) is equivalent to

N +

_E T ₂ 0

where

N =

C

E T ( t ) [ 0 h i J +

C T

- 1

H

, E f ( t ) [ E 2 0 ] < 0 _

у t        t b t b t t 1                t t        t b t b t t 1

+aM_iBc_l b T m T + k^-1 ph Hl p + y pBi B I p b2t b2t t        1t

+k t E T 1 E t 1 .

It is obvious that there must exist positive scalars s _t >  0

_{£ i}HHI - 1 <  0,           (12)

where

A =I в [ A - a BaB l MI J = 1

n= P t ^{- 1} k

M t = P t ^-XY¹

N = [ H 1 Q L H m Q QC T L QC I J

R = II P t [ s-¹ QE l E. 2 Q + a t QM t B _fi, B I^ M l Q i =1 ^{L                                                   1 t}

+ k QE T E 1 Q J

L = [ ^- M 1 1 , ^L , ^- M m I ]

W = dtag { - П 1 1 ,L , -n _mI , e - ( S 1 H 1 H T - 1 ),L , P m ( £ „ H_mH^Ti - 1 ) }

(G = [ G 1 L G m ]

^Gm =[^ B m ^B 2 m J

M is any appropriate dimensions matrix. Then there exist feedback controller u_t = k_tx and a switching law

ст : R + ^ M = { 1,2, K , m } such that the closed-loop system of system (10) for all admissible actuator failures is quadratically stable and the controlled output z satisfies II z\ 12 <  Y H 12 ■ Control gain k i = - 0.5 a i B T Q .

Remark 1 Consider system (10), by using output feedback control u i = k i y , the closed-loop system of system (10) for all admissible actuator failures is quadratically stable and the controlled output z satisfies II z | 12 <  Y H 12 , then there must exist positive scalars

P i , a i , ^ i , s i , у and a symmetric positive definite matrix Q , such that (11) (12) hold, control gain k i = - 0.5 a i B T QC ^- .

• IV.    N UMERICAL E XAMPLE

To demonstrate the effectiveness of the design controller proposed in this paper, we consider the following uncertain switched linear systems:

Subsystem 1 ：

x( t ) = ( 1

- 5 - 3

0 ]

+

" 0.1 . 0

0 " 0.1

H 1

( t )

" 0.5 . 0

0 " 0.6 _

^ x ( t ) +

" 0 .- 1

0.5 " 0 ]

H 1 ( t ) +

" 2 1 " . 1 0 _

u 1 ( t )

" 1.5

2 "

" 0.1

0 "

" 0.2

0 "

z ( t ) = 1 i        V

.- 2

0 ]

+

0

0.1 ]

5

( t )

0

0.3 ]

^ x ( t )

(

" 1

0 ")

y ( t ) = 1

0

JJ

x ( t )

. x ( t 0 ) = x 0

Subsystem 2 ：

' A . ) = (	" 1 0	- 2 " - 3 ]	+	" 0.1 0 " . 0 0.2 _	S 2( t )	" 0.1 . 0	0 " 0.6 ]	) x ( t ) +	" 1 . 0
(	" 0	- 4		" 0.1 0	"	" 0.1	0
z ( t ) = 1 i y ( t ) =[ V x ( 1 0 ) =	.- 1 0 x 0	0 11	+ 0 0.2 x ( t )		= , ( t ) . 0		0.1	^ x ( t )

- 1.5

^H 2 ⁽ t ) +

u ₂( t )

where

5 1 ( t ) =	" sin( t )           "	, 5 2 ( t ) =	" 0.9sin( t )
	.           cos( t ) _		.               sin( t )

Here, if the H „ norm bound is assumed to be у = 1 , choose

Ц = {2}; Q2 ={1};

s 1 = 0.1; s ₂ = 0.1; ^ = 0.2; £ = 0.5;

a 1 = 8; a ₂ = 6; P 1 = P 2 = 0.5.

The matrix A 1 and A 2 have egienvalues { - 5,1 } and { 1, - 3 } , respectively. Therefore, the matrix A 1 and A ₂ are unstable. It is required to design the state feedback controller with (6) that can robustly stabilize the uncertain switched system (1) with disturbance attenuation у , not only when all actuators are operational, but also when some actuators experience failures within the prescribed set of susceptible actuators.

By solving (4) and (5), we can get the following matrices:

Hence, from the Theorem 1, state feedback controllers can be constructed as

	" -50.7322 -34.0031 "
u 1 ( t ) =		x ( t )
	. -21.3103 -8.1116 ]
	" -54.0319 -31.5 860 "
u 2 ( t ) =		x(t)
	. -28.1501 -32.7535 _

The switching law is when x T ( N 1 - N ₂) x <  0 ,

P =

5.3276

2.0279

2.0279

4.4450

subsystem 1 is active and when x^T ( N 1 - N ₂) x >  0 subsystem 2 is active.

The simulation result for the closed-loop system is show in the following figures. Note that the initial (state) conditions are x 0 =[1.5 -3.5]T

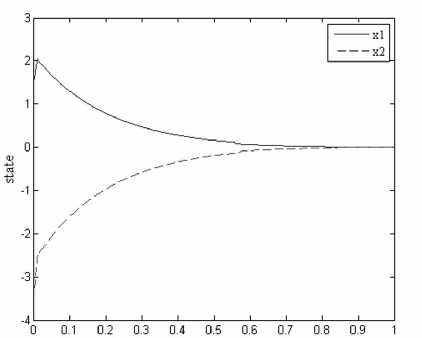
Fig.1 and 2 show the state response under reliable controller in the cases of actuators failures and of no failures, respectively. Obviously, reliable controller can guarantee the quadratically stability of the closed-loop system for such two cases. Furthermore, we can see from Fig.1 and 2 that response performance of the system without failure is better than that of the systems with failures. Fig.3 depicts the state response of the uncertain switched system with failures in actuator and external disturbances under the conventional controller. The trajectory of uncertain switched system is shown in Fig. 4, while Fig. 5 gives the switched signal of the uncertain switched system with failures in actuator and external disturbances, when reliable controller work.

time(second)

Figure 1. The state responses of reliable controller with failure

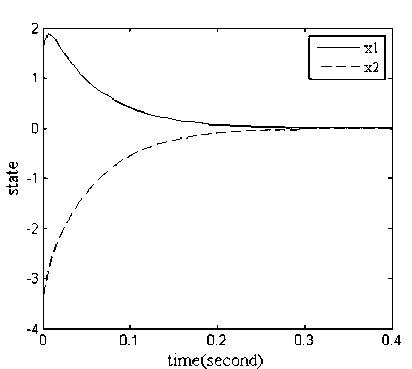
Figure 2. The state responses of reliable controller without failure

• V.    C ONCLUSIONS

This paper focuses on the problem of H _∞ reliable control design for switched linear systems with parameter uncertainties and external disturbances. An approach based on LMI method and convex combination technique is given such that the problem is solved. The resulting systems are reliable in that they provide guaranteed quadratically stability and H _∞ performance. A numerical example had been illustrated to show the validity of our results.

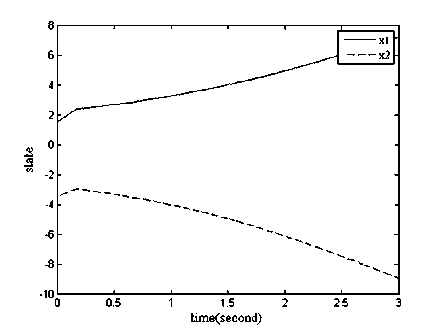
Figure 3. The state responses of conventional controller with failure

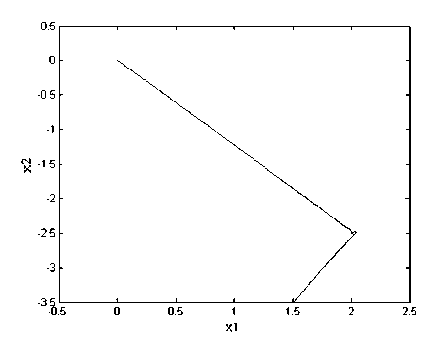
Figure 4. The state trajectory of reliable controller with failure

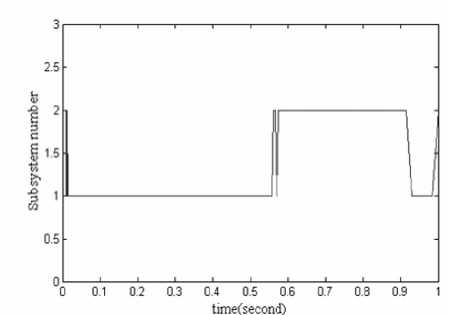
Figure 5. The switched signal of reliable controller with failure

A CKNOWLEDGMENT

This work is supported by the Research and Development Foundation form Jinling Institute of Technology under Grant No：jit-n-2009012. I would like to express my heartfelt gratitude to Associate Professor Z. R. Xiang and R. H. Wang, who gave me a lot of help in the process of writing papers. At the same time, the authors wish to thank the referees for their constructive suggestions and for information on previous work.