Роль базовых математических моделей в эволюционной экономике

В последние годы в области анализа динамических экономических процессов, к числу которых относятся и инновационные процессы в сфере туризма, происходит постепенный отказ от неоклассического подхода, заложенного А. Маршаллом еще в начале XX века [18], и переход к эволюционному подходу.

При использовании этого подхода изучаемый экономический объект рассматривается как система, которая постоянно претерпевает изменения. При анализе развивающихся систем используются динамические модели с дискретным или с непрерывным временем. В первом случае изменение переменных задается разностными, а во втором – дифференциальными уравнениями. Принципиально важным моментом при использовании эволюционного подхода является возможность отражения в соответствующих динамических моделях эволюционных механизмов развития.

Существенной особенностью динамических моделей многих экономических процессов, в том числе и в сфере туризма, является их нелинейность, вследствие чего эти модели, как и сами процессы, могут иметь несколько состояний равновесия, устойчивых и неустойчивых. Поэтому метод сравнительной статики может быть эффективен лишь до тех пор, пока характер стационарного решения динамической модели не меняется кардинальным образом при малом изменении ее параметров. Если это условие нарушается, то при исследовании экономических процессов следует использовать эволюционный подход с привлечением методов нелинейного динамического анализа и теории развивающихся систем.

Методологической основой эволюционного подхода служит современное направление теоретических исследований, которое носит название эволюционная экономика [5, 10, 16, 17, 19, 20].

Основные принципы эволюционной экономики были взяты из биологии, т. к. эволюционная теория Ч. Дарвина как научная доктрина первоначально возникла в этой науке [4].

Перечислим важнейшие положения теории Дарвина [6].

• 1.    Организмам свойственна наследственная изменчивость. Наиболее обычной и важной формой изменчивости является неопределенная. Стимулом для возникновения изменчивости организмов служат изменения внешней среды, но характер изменчивости определяется спецификой самого организма, а не направлением изменений внешних условий.

• 2.    В центре внимания эволюционной теории должны находиться не отдельные организмы, а биологические виды и внутривидовые группировки (популяции).

• 3.    Все виды организмов в природе вынуждены вести жестокую

• 4.    Неизбежным результатом наследственной изменчивости организмов и борьбы за существование является естественный отбор -преимущественное выживание и обеспечение потомством лучше приспособленных особей. Хуже приспособленные организмы (и целые виды) вымирают, не оставляя потомства.

• 5.    Следствиями борьбы за существование и естественного отбора являются: развитие приспособлений видов к условиям их существования (обусловливающее "целесообразность" строения организмов), дивергенция (развитие от общего предка нескольких дочерних видов, все большее расхождение их признаков в эволюции) и прогрессивная эволюция (усложнение и усовершенствование организации).

• 6.    Частным случаем естественного отбора является половой отбор, который обеспечивает развитие признаков, связанных с функцией размножения.

• 7.    Породы домашних животных и сорта сельскохозяйственных растений созданы посредством искусственного отбора, аналогичного естественному отбору, но ведущегося человеком в своих интересах.

борьбу за свое существование. Борьба за существование для особей данного вида складывается из их взаимодействия с неблагоприятными биотическими и абиотическими факторами внешней среды, а также из их конкуренции между собой. Последняя является следствием тенденции всякого вида к безграничному размножению и огромного «перепроизводства» особей в каждом поколении. По Дарвину, важнейшей является именно внутривидовая борьба.

Не углубляясь в теорию Дарвина, на ее критику и развитие, отметим, что о применении биологических аналогий в экономике говорил еще в первой четверти прошлого века А. Маршалл [18]. Приведем его слова: “...Меккой экономиста является скорее экономическая биология, нежели экономическая динамика. Но биологические концепции более сложны, чем теории механики. Поэтому в книге «Об основах экономической теории» следует уделить относительно большее место аналогиям из области механики, приходится часто использовать термин “равновесие”, что предполагает некоторую аналогию со статикой. Это обстоятельство ... создает впечатление, будто ... центральной идеей <книги> служит “статика”, а не “динамика”. Но в действительности наше исследование целиком посвящено силам, порождающим движение, и основное внимание в нем сосредоточено не на статике, а на динамике” [18].

Использование биологических аналогий не ограничивается общенаучными обобщениями: оказывается, что некоторые экономические процессы и те или иные биологические процессы развития формально описываются одинаковыми (или близкими) математическими моделями. В этом случае, если модель соответствующего биологического процесса уже исследована, целесообразно использовать результаты этого исследования, рассматривая их как отправную точку при анализе изучаемого экономического объекта.

Эволюционная экономика опирается на использовании в экономических исследованиях свойственных современной эволюционной биологии методологических подходов и рассмотрение процесса хозяйственных изменений в терминах «естественного отбора» среди популяции субъектов (фирм и других организаций) [10].

При использовании эволюционного подхода предполагается, что в экономической системе существуют аналоги механизмов наследственности, изменчивости, естественного отбора и разнообразия, а экономические агенты конкурируют друг с другом за общие ресурсы.

К числу первых работ в области экономики, авторы которых обращались к эволюционным идеям, можно отнести, прежде всего, статьи Т. Веблена «Почему экономическая наука не является эволюционной дисциплиной?» (1898), статью А. Алчиана «Неопределенность, эволюция и экономическая теория» (1950), впервые опубликованные на русском языке в альманахе [11], и книгу Й. Шумпетера [21]. Современный этап развития эволюционного подхода в экономической науке принято связывать с опубликованными в 1960-1970-х гг. работами С. Уинтера, посвященными критической оценке основных постулатов неоклассической теории фирмы. Однако в качестве самостоятельной научной школы эволюционная теория оформилась лишь в середине 1980-х гг., после выхода в свет книги Р. Нельсона и С. Уинтер [19].

Наиболее важным новшеством, связанным с использованием эволюционных концепций, является отказ от понятия репрезентативного хозяйствующего субъекта и рассмотрение процессов, ведущих к возникновению и изменению с течением времени вариации индивидуальных признаков субъектов (моделей поведения фирм, технологических параметров их деятельности).

Благодаря указанному подходу концептуальная схема анализа микроэкономических проблем созданная в рамках эволюционной теории, оказывается принципиально отличной от неоклассической. В эволюционной теории вводится ключевое понятие относительно стабильных в краткосрочной и среднесрочной перспективе организационных рутин – используемых фирмами стандартных правил и процедур ведения деятельности, фиксирующих методы получения информации, выработки и проведения в жизнь стратегических и тактических решений, распределения задач между исполнителями и т. д. Использование рутинных процедур позволяет экономить ресурсы, необходимые для принятия решений в многократно повторяемых ситуациях, хотя порой оно приводит к тому, что принятые решения оказываются неоптимальными. В этом аспекте эволюционная теория, безусловно, отказывается от принятых в неоклассической теории представлений о «гиперрациональности» экономических субъектов, позволяющей их всегда действовать оптимальным способом. Напротив, эволюционная теория подчеркивает важность фактора случайных ошибок, составляющих неотъемлемую часть как процесса накопления опыта хозяйственной деятельности, так и самого процесса эволюции.

Отказ от представления о совершенной рациональности хозяйствующих субъектов и выдвижение на первый план фактора организационных рутин обусловливает в рамках эволюционной теории фундаментальный вывод о том, что результат эволюционного процесса не обязательно соответствует принципу максимизации эффективности [5, 10, 16, 17, 19, 20].

Важным направлением анализа является построение так называемых моделей шумпетерианской конкуренции, связанных с учетом таких характеристик конкурентного процесса, как сопряженные с издержками усилия по осуществлению и имитации инноваций, а также по присвоению выгод от инновационной деятельности. При этом моделируется отбор двух типов организационных рутин: с одной стороны, рутин, управляющих использованием фирмами ресурсов при заданном продуктовом наборе и заданной технологии, и, с другой стороны, рутин более высокого уровня, на которые опирается процесс создания новых продуктов и разработки новых производственных технологий.

Эволюционная теория претендует сейчас на статус одного из основных течений в экономической науке. Такие ее понятия, как «организационные рутины», «фирмы-инноваторы» (лидеры, осуществляющие первый «запуск» инновации), «фирмы-имитаторы» (последователи, которые перенимают уже появившуюся на рынке инновацию) и др., получают все большее распространение в научных работах. Растет влияние эволюционной экономики и на анализ конкретных экономических процессов: методы теории развивающихся систем, используемые в эволюционной экономике, в настоящее время все шире применяются при анализе динамики различных экономических процессов, в том числе и в сфере туризма [7, 12, 13, 14]. Применение этих методов открывает новые возможности для анализа влияния различных факторов на эволюцию изучаемого экономического объекта.

Примером применения биологических аналогий в экономике является использование при изучении инновационных процессов моделей распространения инноваций эпидемиального типа [1, 22, 23]. В моделях эпидемии, разработанных и исследованных в математической биологии, отражен процесс перехода части популяции из одной группы в другую.

Так, в основе модели эпидемии Бэйли, являющейся одной из простейших моделей популяционной динамики, лежит блок-схема, приведенная на рис. 1 [1]. Здесь предполагается, что некоторая популяция, обитающая в замкнутом ареале и численность которой Ng считается неизменной, подверглась эпидемии. Вся популяция, подразделяется на три группы.

В первую из них включены особи в количестве N_± (t) , которые здоровы, но восприимчивы к этой болезни. Вторую группу составляют особи в количестве N₂( t) , которые больны и являются источником распространения

Здоровые, неболевшие

Больные

Выздоровевшие ►

Рис. 1. - Концептуальная схема модели эпидемии Бейли заболевания. Третью группу в количестве N3(t) составляют особи, которые выздоровели и не подвержены опасности заболевания благодаря приобретенному иммунитету. Предполагается также, что длительность заболевания рассматриваемой популяции ограничена, и через некоторое время больные особи выздоравливают, приобретая иммунитет к данной болезни.

В модели эпидемии отражен процесс перехода части популяции из одной группы в другую по следующей схеме. При этом часть особей первой группы (здоровые, неболевшие) заболевает из-за контактов с особями второй группы (больные), вследствие чего численность первой группы сокращается, а второй увеличивается за счет притока новых больных. Поскольку при этом непрерывно происходит процесс выздоровления, выздоровевшие особи пополняют численность третьей группы, одновременно сокращая численность больных. Предполагая, что что при достижении некоторого предельного значения N * , особи первой группы становятся невосприимчивы к болезни, приходим к системе дифференциальных уравнений, определяющей динамику эпидемии:

^i _ f-aNi, если Ni(t) > N*, dt   [ 0, если N((f) < N*,

dN2 _ С aN — b N2, если ^(t) > N*,dt   [ — bN2, если ^(t) < N*,

^ = b N₂                          (3)

■

Решением системы дифференциальных уравнений (1) – (3) с заданными начальными условиями ^(o) = Ns — N20, N2(0) = N20, N3(o) = 0 являются функции Ni(t),N2(t) и N3(t). Особенностью этого решения является следующее. Переменная ^(t) - число неболевших особей -монотонно уменьшается до уровня *, число выздоровевших монотонно растет до значения Ns — N*, а число больных сначала растет, а затем падает до нуля (рис. 2, слева). При этом общее число здоровых особей сначала уменьшается, достигает некоторого минимума, а затем начинает увеличиваться (рис. 2, справа).

Правомерность использования биологической аналогии при изучении инновационных процессов определяется тем, что жизненный цикл нововведения и массовое протекание некоторых болезней характеризуется тремя стадиями: появление, развитие и распространение, угасание. Модели инновационных процессов эпидемиального типа и некоторые другие модели, в основе которых лежат взятые из биологии идеи конкуренции,

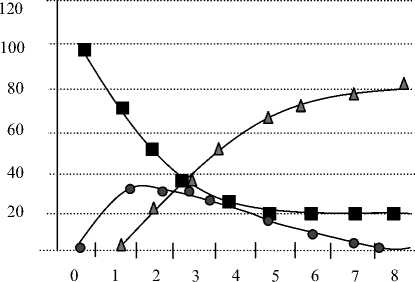
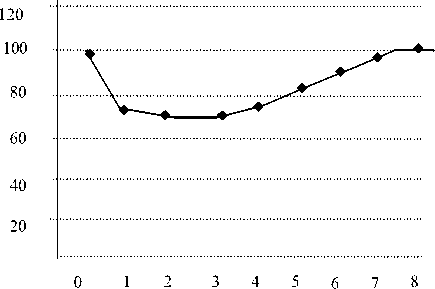
—■ N1 ж N2 —о N3 N1+N3

Рис. 2. Динамика переменных в модели эпидемии сосуществования и др., используются для целей прогноза и управления, для оценки конкурентоспособности замещающих продуктов или технологий [1, 23]. Ниже будет показано, что использование даже простых линейных динамических моделей при реализации эволюционного подхода имеет существенное преимущество по сравнению с традиционным анализом, опирающимся на неоклассический подход.

Особое место в любой науке занимают базовые математические модели, такие, как модели теории катастроф, одномерных отображений и др. [2, 3, 8, 9, 18, 24]. Примером базовой модели служит и рассмотренная выше модель эпидемии.

Базовые математические модели издавна играют важную роль при исследовании процессов любой науки. Например, нобелевский лауреат Г. Лоренц, один из основоположников теории относительности, обсуждая достоинства таких моделей в книге “Элементы высшей математики”, отмечал следующее. “... Чем больше число условий, от которых мы отвлечемся, чем малочисленнее будут факторы явления, тем больше шансов достичь конечной цели исследования – установить не только качественную, но и строго определенную количественную зависимость изучаемого объекта от определяющих его факторов; тогда получится возможность взвесить действие каждого из них отдельно и предвидеть с математической точностью результаты данной комбинации условий” [15].

Значение базовых математических моделей определяется, таким образом, следующими обстоятельствами.

Во-первых, базовые модели служат основой и мягких моделей небольшой размерности, и более точных и полных многомерных (имитационных) моделей, являясь упрощенными частными случаями последних.

Во-вторых, базовые модели, несмотря на свою относительную простоту, отражают основные особенности исследуемого процесса, а результаты их анализа интерпретируемы. Поэтому такие модели могут быть использованы для изучения механизмов развития сложных процессов и возможных изменений, в том числе достаточно резких и катастрофических.

В-третьих, при рассмотрении динамических процессов базовые модели позволяют исследовать влияние нелинейности и, в ряде случаев, обнаружить неочевидные (и даже неожиданные) их свойства. А это очень важно для понимания механизмов развития многих процессов экономики, т. к. в этой области результаты не всегда пропорциональны прилагаемым усилиям.

В-четвертых, изучение базовых моделей способствует развитию “...специфически нелинейной интуиции, основанной на порой парадоксальных выводах нелинейной теории” [2].

Многие процессы, изучаемые в гуманитарных науках, где в последние десятилетия были построены и исследованы, в частности, математические модели мобилизации, циклического развития социокультурных процессов, модели взаимодействия народа и правительства, модели гонки вооружений, модели распространения наркотиков и другие, относятся к сложным.

Сложными является и большинство экономических процессов, в том числе процессов развития индустрии туризма. Поэтому базовые модели играют заметную роль при изучении развития индустрии туризма.