Роль "Биометрии" Н.А. Плохинского в количественной экологии
Автор: Розенберг Г.С., Костина Н.В., Иванова А.В.
Журнал: Самарская Лука: проблемы региональной и глобальной экологии @ssc-sl
Статья в выпуске: 3 т.33, 2024 года.
Бесплатный доступ
Рассматриваются этапы становления биометрии - статистических метод выявления влияния отдельных факторов на результат эксперимента. Обсуждаются особенности дисперсионного анализа (ANOVA), который позволяет сравнивать средние значения трёх и более групп.
Биометрия, «лысенковщина», дисперсионный анализ, алгоритм
Короткий адрес: https://sciup.org/148330455
IDR: 148330455 | УДК: 51-76:57.087.1 | DOI: 10.24412/2073-1035-2024-33-3-64-74
Текст научной статьи Роль "Биометрии" Н.А. Плохинского в количественной экологии
С госпожой Биометрией не заскучаешь!
Юрий Владимирович Линник (1944-2018), поэт, философ-космист [Линник, 2014, С. 79].
40. Программы без ошибок можно написать двумя способами, но работает – только третий. – There are two ways to write error-free programs; only the third one works.
76. Не создатели, а пользователи должны параметризовать процедуры. – It is the user who should parametrize procedures, not their creators.
Алан Перлис (Alan Jay Perlis; 1922-1990), американский учёный в области информатики, первый лауреат премии Тьюринга [Perlis, 1982, p. 9, 11].
университета, открыта 14 июня 1899 г.; см. далее); под фотографией приведено латинское высказывание “Ignoramus, in hoc signo laboremus” – «Мы не знаем, так что давайте работать», иногда приписываемое Дарвину. Следом за этим шли научные статьи (около 500 страниц); среди авторов первого номера – К. Пирсон, Р. Уэлдон (W.F. Raphael Weldon; 1860-1906), Э. Браун (Edward Thomas Browne; 1866-1937), О. Латтер (Oswald Hawkins Latter; 1864-1948) и др. специалисты (б о льшей частью – генетики).
Принято считать (Мизинов, Коннова, 2023), что автором термина «биометрия» в его прямом лексическом значении – «расчёт продолжительности жизни» (от др.-греч. βίος – жизнь и μετρέω – измеряю) – является англиканский священник, философ и историк науки У. Уэвелл (William Whewell; 1794-1866). Именно в его письме, которое он направил 12 ноября 1831 г. коллеге, математику, банкиру и адвокату сэру Д. Лаббоку 64
(John Lubbock; 1803-1865), впервые (по крайней мере, в англоязычной литературе) упоминается слово «биометрия» (Todhunter, 1876, р. 135): “I send you some memoirs which I have received for you in a pacquet from Quetelet2. By the way there is a problem in Biometry (if you choose to call your calculations on lives by a Greek name) which may perhaps be included in something you have done,

and if so, I should be glad if you would point out the solution.” – «Я посылаю вам некоторые мемуары, которые я получил для вас в посылке от Кетле. Кстати, в Биометрии (если вы решите назвать свои расчеты жизней греческим именем) есть проблема, которая, возможно, включена в что-то из того, что вы сделали, и если так, я был бы рад, если бы вы указали решение».
В нашей стране курс «Введение в биометрию» десять лет (1919-1929, до момента, когда его отправили в ссылку) читал в Московском университете С.С. Четвериков, один из создателей популяционной генетики. Во времена лысенковщины вместе с генетикой в опалу попала и биометрия, получившая клеймо «извращения математики на службе менделизма». Не помогло даже заступничество академика А.Н. Колмогорова, который
2 A. Кетле (Lambert-Adolph-Jacques Quetelet; 1796-1874) – бельгийский математик, астроном, социолог. Один из родоначальников научной статистики (Розенберг, 2021).
опубликовал в «Докладах Академии наук СССР» статью «Об одном новом подтверждении законов Менделя» с математическим анализом большого объёма экспериментальных наблюдений генетиков (Колмогоров, 1940). Уже в следующем номере «Докладов» вышла статья самого Лысенко; в ней он писал: «Автор ( Колмогоров. – Г.Р .), желая доказать "верность" и незыблемость статистического закона Менделя, приводит ряд математических доводов, формул и даже кривых. Я не чувствую себя достаточно компетентным, чтобы разбираться в этой системе математических доказательств… Мне хочется лишь указать, что нас, биологов, не интересуют математические выкладки, подтверждающие практически бесполезные статистические формулы менделистов» (Лысенко, 1940, с. 834). Сейчас трудно поверить в подобный уровень научной дискуссии, но так было (Петухова, 2021).
Свою лепту в разгром отечественной биометрии внёс ещё один достаточно одиозный деятель, о котором не часто вспоминают, описывая эти события. Это – Э.Я. К о льман.
Эрнест Кольман родился в Праге (тогда Австро-Венгрия) в семье почтового чиновника. Учился в Пражском (Карловом) университете, где в 1911 г. слушал лекции самого А. Эйнштейна (Albert Einstein; 1879-1955). В годы Первой мировой войны воевал на русском фронте, попал в плен и остался в Советской России. В 1917 г. стал членом РКП(б). Далее его жизнь выписывала сложные «загогулины»: начальник политотдела 5-й армии РККА, заслан Коминтерном в Германию для подрывной работы, арестован, в 1930 г. вернулся в Москву, работал в Институте красной профессуры, возглавил Ассоциацию институтов естествознания Коммунистической академии (после О.Ю. Шмидта), главный редактор журнала «За марксистско-ленинское естествознание», председатель Московского математического общества (1930-1932), зав. отделом науки при Московском горкоме ВКП(б) (1936-1938); обвинения философского и политического характера (доносы) на многих известных деятелей науки – В.И. Вернадского, С.И. Вавилова, Л.Д. Ландау, И.Е. Тамма, Я.И. Френкеля, Н.Н. Лузина и мн. др., преподавание математики в Московском энергетическом институте и работа в Институте философии АН СССР, после Великой Отечественной войны направлен в Прагу на пост заведующего отделом пропаганды ЦК Компартии Чехословакии, профессор Карлова университета («внедрял» диалектику, исторический материализм, после Февральского переворота 1948 г. в Чехословакии и прихода к власти Компартии руководил изгнанием из университета неугодных коммунистам профессоров 65

Колмогоров Андрей Николаевич (1903-1987)
( все фото, примерно, начала 40-х гг. )

Лысенко Трофим Денисович (1898-1976)
К о льман Эрнест Яром и рович (Arnošt Kolman; 1892-1979)
и «чисткой» состава студентов, перестарался, по личной жалобе руководителя компартии и страны К. Готвальда (Klement Gottwald; 18961953) И.В. Сталину был арестован, препровождён в Москву, пробыл в тюрьме 3,5 года; после освобождения, с «подачи» Н.С. Хрущёва, был направлен вновь на работу в ЧССР директором Института философии АН Чехословакии, был избран академиком АНЧ, но через два года вышел на пенсию и вернулся в Москву; в 1976 г. выехал в Швецию, чтобы повидать свою дочь, и стал «невозвращенцем», получив политическое убежище, остановив своё 58-летнее членство в коммунистической партии; 8 октября 1976 г. написал «Открытое письмо Леониду Брежневу. Почему я выхожу из коммунистической партии», 9 декабря 1976 г. был исключён из АНЧ; скончался в Стокгольме 22 января 1979 г. (см. [Ба-гоцкий, 2022] и Википедию). Чтобы получить представление о взглядах Кольмана периода 30-40-х годов, приведем пару цитат. «Не менее характерной чертой, чем грубая подделка под "советский стиль", является исключительное обилие математических вычислений и формул, которыми так и пестрят вредительские работы. <…> "Материя исчезает, остаются одни уравне-ния"3 – эта ленинская характеристика ученой поповщины в современной физике дает ключ к пониманию вредительского пристрастия к математизации любой науки. На самом деле, не станут же вредители писать прямо, что они за реставрацию капитализма, должны же они искать наибо- лее удобной маскировки. И нет более непроницаемой завесы, чем завеса математической абстракции. Математические уравнения сплошь да рядом придают враждебным социалистическому строительству положениям якобы бесстрастный, объективный, точный, неопровержимый характер, скрывая их истинную сущность» (Кольман, 1931, с. 75). И в дополнении к ответу Лысенко – Колмогорову: «Разумеется, что с точки зрения формально-математической работа А.Н. Колмогорова, одного из виднейших совет-ских4 и мировых математиков, создавшего наиболее совершенную теоретико-множественную аксиоматизацию теории вероятностей, является абсолютно безупречной и предлагаемый им метод проверки указанных статистических данных значительно превосходит простую проверку по квадратическому уклонению. <…> К сожалению, А.Н. Колмогоров не ограничивается этой математической стороной, а здесь же делает выводы, выходящие за пределы математики, высказывается в пользу менделевско-моргановской генетики. <…> Причиной, приведшей А.Н. Колмогорова к неверным выводам, является, по-видимому, прежде всего его методологическая установка в вопросе о роли теории вероятностей и статистики в исследовании процессов материального мира. <…> поскольку менделевские законы являются законами биологическими, никакое статистико-математическое доказательство (или опровержение) дать им невозможно» (Кольман, 1940, с. 836, 837, 840).
4 В 1939 г. А.Н. Колмогоров был избран действительным членом (академиком) АН СССР, минуя «ступень» чл.-корр. АН СССР.
Осенью 1955 г. по инициативе сотрудников БИНа АН СССР В.Я. Александрова и Д.Б. Лебедева, а также генетика из ЗИНа АН СССР Ю.М. Олёнова5 было написано письмо в Президиум ЦК КПСС, в котором раскрывалась отрицательная роль Лысенко в биологии. Письмо подписали 297 известных ученых (поэтому его называют «Письмо трехсот»). Авторы писали об огромном вреде, нанесённом отечественной биологической науке, материальных и моральных потерях, которые понесла страна в результате деятельности Т.Д. Лысенко и его приспешников (Жимулёв, Дубинина, 2005; Кузнецов, 2006, с. 62-64): «Материальные потери, которые понесла наша страна в результате деятельности Т.Д. Лысенко, не поддаются исчислению, так они велики <…>. Взамен современного дарвинизма Т.Д. Лысенко выступил со средневековой, позорящей советскую науку теорией «порождения видов». <…> Особенно плохо обстоит дело с использованием статистических методов в биологии. Это приводит к ложным теоретическим выводам и не обоснованным практическим рекомендациям. <…> Попытка академика А.Н. Колмогорова наладить правильное применение статистики в биологии была отвергнута академиком Т.Д. Лысенко чисто аракчеевскими приемами » (Жимулёв, Дубинина, 2005, с. 16, 18, 29; выделено нами. – Авторы ).
Но вернемся к биометрии. В период «оттепели» и после на русском языке вышел ряд удачных монографий и учебников по биометрии (Ро-кицкий, 1964; Урбах, 1964; Плохинский, 1970; Терентьев, Ростова, 1977; Доспехов, 1985; Лю-бищев, 1986; Лакин, 1990); стали выходить книги по биометрическим методам применительно к отдельным направлениям биологии (например, в геоботанике [Грейг-Смит, 1967; Василевич, 1969; Миркин, Розенберг, 1978]). В XXI в. появился еще ряд достойных учебных пособий по биометрии (Пузаченко, 2004; Сиделев, 2012; Ивантер, Коросов, 2013; Соколов и др., 2018).
Среди этих изданий достойное место занимает учебник Н.А. Плохинского, юбилею которого (125 лет со дня рождения) и посвящён этот обзор.

Николай Александрович Плохинский родился 1 декабря 1899 г. в селе Николо-Дол Калужской губернии. Его родители – директор школы Александр Иванович и учительница Мария Васильевна. В 1918 г. Николай с отличием окончил Калужское реальное училище, устроился практикантом на Петровскую ферму и поступил в Петровскую сельскохозяйственную академию. Из академии он перешел на курсы зоотехников Наркомзема и в 1920 г. был направлен в губзем-отдел Калужской области инструктором по скотоводству, а затем стал заведующим володарского племенного рассадника швицкого6 скота.
С 1921 по 1924 гг. Николай Александрович учится в Московском зоотехническом институте, в котором остается работать7; с 1928 г. он становится ассистентом, а с 1934 г. – доцентом кафедры зоологии 2-го Московского государственного университета. Далее – работа научным сотрудником во Всесоюзном институте животноводства; именно там у него проявляется интерес к статистике, возможностям обработки данных. В 1935 г.
Н.А. Плохинский становится кандидатом сельскохозяйственных наук, а в 1937 г. выходит в свет первая книга по биометрии – учебник «Статистические методы в зоотехнии» (Плохинский, 1937). В 1941 г. – эвакуация и работа зоотехником-селекционером в Ярославском госплемрассадни-ке. С 1945 по 1946 гг. – доцент кафедры частного животноводства Московского пушно-мехового института; далее – старший научный сотрудник ВНИИ мясной промышленности (Васильева, 1999).
«Во времена гонений на генетику она ( З.С. Ни-коро [1904-1984], генетик, педагог. - Авторы ) и Н.А. Плохинский потеряли работу и вместе подрабатывали музыкой в ресторанах: она – на скрипке, он – на фортепиано» (Животовский, 2023, с. 100).
В 1958 г. Плохинский переезжает в Новосибирск и работает в Институте цитологии и генетики СО АН СССР над созданием лаборатории генетических основ селекции животных, которую и возглавляет. В 1961 г. в Новосибирске выходит в свет первое издание «Биометрии» (Плохин-ский, 1961).
В 1962 г. он уезжает обратно в Москву, где работает профессором-консультантом на кафедре генетики и селекции биологического факультета МГУ, преподает биометрию. Здесь выходят в свет его монографические работы по биометрическим методам исследования (Пло-хинский, 1978, 1980).
Скончался Николай Александрович Плохин-ский в 1988 г.
Во «Введении» своей этапной работы Н.А. Плохинский (1970, с. 3) пишет: «Имеются такие задачи современной биологии, которые не только не могут быть решены без математики, но и трудно понимаемы без соответствующей математической подготовки. Например, очень глубокое и ценное понятие о наследуемости без знания основ дисперсионного анализа обычно воспринимается с большим трудом, далеко не всегда правильно, что часто приводит к ошибочным выводам и неподтверждающимся прогнозам как в теории, так и на практике. Новейшие вопросы биологической теории – теория популяций, математическое моделирование биологических процессов – не могли бы даже и возникнуть без разработки специальных математических методов. Современный биолог должен знать основы математики». Тираж этой книги (11 тыс. экз.) удовлетворил практически всех желающих.
В большинстве случаев биометрия, по своей сути, – это математическая статистика. А это, в свою очередь, выбор между гипотезами. В качестве двух основных характеристик любой биометрической системы можно принять ошибки первого и второго рода. В биометрии наиболее устоявшиеся понятия – FAR (False Acceptance Rate; коэффициент ложного принятия неверной гипотезы) и FRR (False Rejection Rate; коэффициент ложного отклонения верной гипотезы).

Учебник «Биометрия» состоит из четырёх частей: «Основы биометрии», «Биометрические методы», «Алгоритмы биометрических расчётов» и «Математические таблицы». Цель книги – показать применение методов математической статистики при обработке и анализе числовых результатов экспериментов, наблюдений и производственной отчётности, а также при планировании опытных работ.
В нашей статье мы остановимся только на одном биометрическом методе, который подробно обсуждается Н.А. Плохинским, и который широко используется в экологических исследованиях. Это – дисперсионный анализ.
Из определения «Дисперсионный анализ» в Большой советской энциклопедии: «Статистический метод выявления влияния отдельных факторов на результат эксперимента. Первоначально Д. а. был предложен англ. статистиком Р. Фишером8 (1925) для обработки результатов агрономич., опытов по выявлению условий, при к-рых испытываемый сорт с.-х. культуры даёт максимальный урожай. Современные приложения Д. а. охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистич. теории выявления систе-матич. различий между результатами непо-средств. измерений, выполненных при тех или иных меняющихся условиях» (Большев, 1972, с. 305). Таким образом, в отличие от t-критерия (критерия Стьюдента, который также обсуждается в «Биометрии» и призван оценить достоверность различия средних для двух групп сравниваемого параметра), дисперсионный анализ позволяет сравнивать средние значения трёх и более групп. В литературе также встречается обозначение ANOVA (от англ. ANalysis Of VAriance).
Заслугой Н.А. Плохинского является тот факт, что он дал очень подробные, с элементарными примерами, описания алгоритмов одно-, двух-и трёхфакторных дисперсионных комплексов (с. 62-84). Это позволяло проводить расчёты корреляционного отношения (основной показатель дисперсионного анализа) вручную или с применением самых простых вычислительных средств (например, ЭВМ «Наири» [Розенберг, 1976], не говоря уже о популярном программном продукте STATISTICA [Боровиков, 2013]). Поэтому далее мы не будем останавливаться на описании алгоритмов дисперсионного анализа (см. также [Шеффе, 1980; Любищев, 1986; Розенберг, 2020; Бобков, 2022]), а сразу приведем некоторые примеры их реализации.
Прежде всего отметим, что своеобразным «гимном дисперсионному анализу» в экологических исследованиях можно считать сборник «Биоиндикация: теория, методы, приложения»
(Биоиндикация .., 1994; Розенберг, 2020). В нём рассмотрены различные аспекты теории и современные методы биоиндикации, среди которых ведущее место занимает дисперсионный анализ. С его помощью обработаны данные, где в качестве биоиндикаторов выступают лихе-носинузии, растительные сообщества, комплексы простейших, гидромицетов, зообентоса, сообщества почвенной микро- и мезофауны; в качестве индицируемых факторов выступают естественные и антропогенные процессы (среди последних – в первую очередь те, которые связаны с загрязнением среды и рекреационной нагрузкой).
В работе (Иванова и др., 2022) рассматривается группирование 36 локальных флор (ЛФ), каждая на пробной площади 400 км2, в средней части Волжского бассейна (на территории Республик Татарстан, Мордовия, Чувашия, а также Самарской, Ульяновской и Пензенской областей). Видовой состав каждой из ЛФ изучался в течение ряда лет (2004-2021). Среднее значение числа видов на пробных площадях для изучаемой территории составляет 684 вида. Изменение флористического состава на изучаемой территории обуславливается плавным изменением параметров среды, в первую очередь, климатическими параметрами. Кластеризация этих ЛФ осуществлялась методом k-средних 9; пространственное размещение выделенных трёх кластеров представлено на рис. 1.
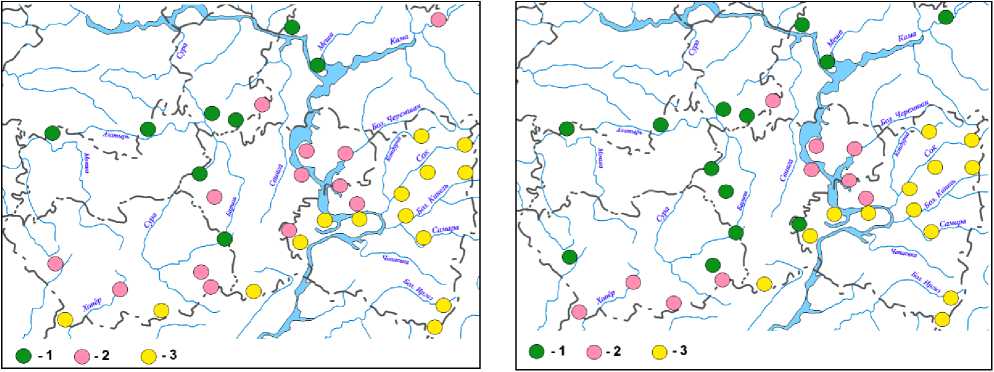
по семейственному спектру ( by family spectrum) по родовому спектру (by generic spectrum)
Рис. 1. Пространственное расположение трёх условно выделенных групп ЛФ сосудистых растений. 1-3 – группы ЛФ (пояснения см. в тексте).
Fig. 1. Spatial arrangement of three conventionally distinguished groups of LF of vascular plants.
1-3 – LF groups (see text for explanations).
Кластеризация осуществлена в пространстве 60 семейств и 35 родов растений. Первая группа9
(рис. 1) объединяет ЛФ, территориально распо ложенные в северной части рассматриваемой тер ритории, большей частью относящейся к Пред ком Г. Штейнхаузом (Hugo Dyonizy Steinhaus; 1887-1972). Подробнее см. (Шитиков, Мастицкий, 2017 [глава 10]; Рындина, 2020).
волжью. ЛФ этой группы демонстрируют Rosaceae -тип спектра семейств. В их составе нет степных сообществ, либо они крайне редки, поэтому разнообразие бобовых минимально. Доля семейства Asteraceae во второй группе выше; часть этих флор имеет Fabaceae -тип, при этом превышение численности бобовых над розоцветными незначительно. Наконец, третья выделенная группа включает флоры лесостепной и степной части Заволжья, а также некоторые ЛФ самой южной части рассматриваемого Предволжья. Все они имеют Fabaceae -тип, причём многие с существенной долей численного отрыва этого семейства от Rosaceae. Доля семейства Asteraceae у этой группы флор самая высокая.
С помощью метода дисперсионного анализа однофакторных комплексов для трёх выделенных в каждом случае кластеров (рис. 1; три градации – три группы ЛФ) определены списки семейств (всего 18) и родов (31), доля видов в которых статистически значимо меняется при переходе от одной группы локальных флор в другую. В табл. 1 представлены результаты для 10 основных объектов.
Сравнительный анализ таксономических спектров и выделение при этом различных флористических «зональностей» важен для понимания экологических закономерностей в пространственном (географическом) распределении флор. Нетрудно видеть, что семейства Asteraceae и Fabaceae тяготеют к третьей группе локальных флор (южная часть Предволжья), а вот Cyperaceae и Orchidaceae – к первой (северо-восток исследованной территории); промежуточное положение (группа 2) демонстрирует семейство Onagraceae.
Таблица 1
Список 10 семейств и родов и их средних значений доли видов (%) по группам локальных флор
List of 10 families and genera and their average value of the share of species (%) by LF groups
|
Семейство |
Группы ЛФ |
η 2 |
||
|
1 |
2 |
3 |
||
|
Asteraceae |
11,6 |
13,7 |
16,3 |
78 |
|
Cyperaceae |
5,9 |
4,0 |
2,9 |
77 |
|
Fabaceae |
4,6 |
5,7 |
7,3 |
64 |
|
Dipsacaceae |
0,2 |
0,3 |
0,5 |
55 |
|
Orchidaceae |
1,6 |
0,6 |
0,4 |
52 |
|
Onagraceae |
1,2 |
1,5 |
0,7 |
50 |
|
Alliaceae |
0,3 |
0,4 |
0,9 |
48 |
|
Asparagaceae |
0,1 |
0,2 |
0,3 |
46 |
|
Geraniaceae |
0,9 |
0,9 |
0,6 |
42 |
|
Juncaceae |
0,3 |
0,1 |
0,2 |
35 |
η2 – сила влияния фактора (%).
|
Род |
Группы ЛФ |
η 2 |
||
|
1 |
2 |
3 |
||
|
Carex |
4,2 |
3,0 |
1,9 |
73 |
|
Astragalus |
0,4 |
0,6 |
1,7 |
71 |
|
Euphorbia |
0,4 |
0,6 |
1,0 |
71 |
|
Artemisia |
0,8 |
1,4 |
1,7 |
63 |
|
Stipa |
0,1 |
0,5 |
0,9 |
61 |
|
Salvia |
0,12 |
0,30 |
0,48 |
59 |
|
Allium |
0,3 |
0,5 |
1,0 |
57 |
|
Inula |
0,4 |
0,5 |
0,8 |
49 |
|
Juncus |
1,1 |
0,9 |
0,6 |
47 |
|
Salix |
1,7 |
1,6 |
1,3 |
42 |
Аналогично можно охарактеризовать группы ЛФ и по родам: Carex , Salix и Juncus чаще встречаются в первой группе, а Artemisia , Astragalus , Allium и Euphorbia – в третьей. Если рассмотреть отдельно какое-либо семейство, например, Asteraceae (в состав этого семейства у ЛФ входит 40-49 родов), то статистически значимо в пределах изучаемой территории меняется состав родов Artemisia, Jurinea, Inula и Serratula , составляющих до 20% всего семейства Asteraceae .
Ещё одна особенность ANOVA. Для однофакторного дисперсионного анализа основное тождество имеет вид: SSобщ = SSA + SSост; для двухфакторного – SSобщ = SSA + SSВ + SSAВ + SSост и т. д. Здесь SSобщ – общая (полная) дисперсия (вариация) результатов, SSX – сумма квадратов отклонений между группами, т. е. вариация, обусловленная фактором (взаимодействием факто- ров) Y; SSост – сумма квадратов отклонений внутри групп (остаточная вариация, вариация неучтенных факторов). Так вот, с увеличением количества учитываемых факторов воздействия в эксперименте число слагаемых (SS) быстро растёт: при одном факторе – их 3, при двух – 5, при трёх – 9, при четырёх – 17, при пяти – 33 и т. д. Упростить такого рода многофакторный ANOVA можно двумя способами. Во-первых, если для этого есть основания, то взаимодействия высокого порядка (по 3, 4, 5 и т. д. факторов) полагают незначимыми и их дисперсии включают в остаточную вариацию (SSост). Второй путь – это объединение факторов в группы и «перевод» схемы дисперсионного анализа в одно-, двух- или трёхфакторный вариант.
Итак, в соответствии с принципом Пилюльки-на 10, дисперсионный анализ «прописывается» практически во всех ситуациях факториальной экологии. Почему ANOVA так важен в экологических исследованиях? Во-первых, как только что было отмечено, можно упростить сложную модель, сделав выводы более наглядными и понятными (Gelman, 2005). Во-вторых , дисперсионный анализ позволяет принять или отвергнуть гипотезу о равенстве всех средних по группе (иными словами, о том, что SS X = 0; правда, здесь следует помнить о возможности совершить ошибку первого или второго рода – FAR и FRR11). Методы математической статистики позволяют отсеять недостоверные гипотезы о структуре и динамике экосистем. Ещё раз подчеркнём, – математическая статистика позволяет только отвергать гипотезы; принятие гипотезы на основе некоторых статистических тестов ещё не означает их справедливость и доказанность (гипотеза может быть только проверена, но никогда не может быть доказана!» [Абросов, Боголюбов, 1988, с. 38]). Наконец, современные широкие компьютерные возможности позволяют обрабатывать огромные массивы данных и использовать некоторые алгоритмы для определения более точных доверительных интервалов, которые были неосуществимы ранее (переход от линейных моделей к существенно нелинейным, нейронным сетям и пр.).
Завершая это эссе, приведём слова профессора Л.А. Васильевой (1999, с. 13): «Отечественная биология именно Плохинскому обязана возрождением такой области научного знания, как биологическая статистика. <…> Вплоть до 1961 года, когда в Академгородке г. Новосибирска в издательстве Сибирского отделения вышла в свет книга под названием "Биометрия", отечественные биологи старшего поколения не пытались, а более молодые и не подозревали, что экспериментальные материалы в обязательном порядке должны подвергаться статистической обработке и статистическому анализу».
И ещё. Хочется вспомнить слова академика ВАСХНИЛ и чл.-корр. АН СССР А.С. Серебров-ского, сказанные сто лет тому назад: «Биолог должен оставаться, прежде всего, биологом и от-

нюдь не превращаться в математика. История статистических исследований в биологии показала, что только там, где исследуемый материал наряду с анализом математическим подвергался интенсивному биологическому анализу, –только там метод дал положительные результаты, продвинув биологов за границы доступного "невооружённому глазу". Безусловно, статистический метод получает права гражданства в биологических дисциплинах. Это внедрение в новые для него области предъявляет самому математическому методы новые требования, удовлетворить которые должны сами математики. И можно не сомневаться в том, что подобное сотрудничество биологов с математиками принесет ещё богатые плоды. <…> Биология и математика образуют не механическую смесь методов, а качественно новый сплав, в котором оба элемента начинают выступать единым мощным фронтом. На определённом этапе развития этого синтеза комплекс новых методов приобретает свои специфические отличии и выделяется в особую отрасль знания. На стыке биологии и математики зарождается новая синтетическая наука с собственным предметом изучения, с особыми основными методами, особыми терминологией, символикой и специфическими задачами. Если отбросить очень неудачный термин "вариационная статистика", то лучше использовать для обозначения этой новой науки более подходящее название – "биометрия", принятое в настоящее время большинством биологов» (Серебровский, 1925, с. 160).
Список литературы Роль "Биометрии" Н.А. Плохинского в количественной экологии
- Абросов Н.С., Боголюбов А.Г. Экологические и генетические закономерности сосуществования и коэволюции видов. Новосибирск: Наука, 1988. 333 с.
- Багоцкий С.В. К юбилеям двух недостойных персон // Химия и жизнь. 2022, № 10. C. 38-44.
- Биоиндикация: теория, методы, приложения / Под. ред. Г.С. Розенберга. Тольятти: ИЭВБ РАН, 1994. 266 с.
- Бобков Н.Н. Лекция 2. Элементы дисперсионного анализа // Дополнительные главы анализа данных. Лекции кафедры математики ГУ ВШЭ. М.: ВШЭ, 2022. С. 1-40. URL: www.hse.ru/data/2010/10/25/ 1222762918Лекция%pdf?ysclid=m46re9g9yg45287700 9 (дата обращения: 01.08.2024).
- Большев Л.Н. Дисперсионный анализ // Большая советская энциклопедия (БСЭ) / 3-е изд. М.: Изд-во «Сов. энцикл.», 1972. Т. 8. Дебитор - Евкалипт. С. 305.
- Боровиков В.П. Популярное введение в современный анализ данных в системе STATISTICA. М.: Горячая линия - Телеком, 2013. 288 с.
- Василевич В.И. Статистические методы в геоботанике. Л.: Наука, 1969. 232 с.
- Васильева Л.А. Памяти Н.А. Плохинского (к 100-летию со дня рождения) // Информ. вестн. ВОГиС. 1999, № 10. С. 13-14.
- Грейг-Смит П. Количественная экология растений. М.: Мир, 1967. 359 с.
- Доспехов Б.П. Методика полевого опыта (с основами статистической обработки результатов исследований). М.: Агропромиздат, 1985. 351 с.
- Животовский Л.А. Твои следы на ландшафтах науки: биография. М.; Йошкар-Ола: Вертола, 2023. 208 с.
- Жимулёв И.Ф., Дубинина Л.Г. К 50-летию «Письма трёхсот» // Вестн. ВОГиС, 2005. Т. 9, № 1. С. 12-33.
- Иванова А.В., Аристова М.А., Костина Н.В., Кузнецова Р.С., Шарая Л.С., Розенберг А.Г., Васюков В.М., Розенберг Г.С. Структура флоры центральной части территории Волжского бассейна по таксономическим показателям // Самарская Лука: проблемы региональной и глобальной экологии. 2022. Т. 31, № 2. С. 40-57.
- Ивантер Э.В., Коросов А.В. Элементарная биометрия. Петрозаводск: Изд-во ПетрГУ, 2013. 110 с.
- Колмогоров А.Н. Об одном новом подтверждении законов Менделя // Докл. АН СССР. 1940. Т. 27, № 1. С. 38-42.
- Кольман Э. Возможно ли статистико-математи-чески доказать или опровергнуть менделизм? // Докл. АН СССР. 1940. Т. 28, № 9. С. 836-840.
- Кольман Э. Вредительство в науке // Большевик. 1931. № 2. С. 71-81.
- Кузнецов В.М. Основы научных исследований в животноводстве. Киров: Зонал. НИИСХ Северо-Востока, 2006. 568 с.
- Лакин Г.Ф. Биометрия: учеб. пособие для биол. спец. вузов / 4-е изд. М.: Высш. шк., 199Q. 352 с.
- Ленин В.И. Материализм и эмпириокритицизм // Полн. собр. соч./ 5-е изд. 1968. Т. 18. С. 7-384.
- Линник Ю.В. Госпожа Биометрия // Принципы экологии. 2Q14. Т. 3, № i (9). С. 78-79. URL: ecopri.ru/article/genpdf.php?id=3402 (дата обращения: 0i.08.2024).
- Лысенко Т.Д. По поводу статьи академика А.Н. Колмогорова («Об одном новом подтверждении законов Менделя») // Докл. АН СССР. 194Q. Т. 28, № 9. С. 834-835.
- Любищев A.A. Дисперсионный анализ в биологии. М.: Изд-во МГУ, 1986. 2QQ с.
- Мизинов П.В., Коннова HX. К вопросу о значении термина «биометрия» // Гуманитарный вестн. 2Q23, № 5. С. i-i i. URL: cyberleninka.ru/article/n/k-voprosu-o-znachenii-termina-biometriya (дата обращения: Q1.08.2024)..
- Миркин Б.М., Розенберг Г.С. Фитоценология. Принципы и методы. М.: Наука, 1978. 211 с.
- Петухова A. Измерение жизни // Коммерсантъ. 2021, 19 февраля. № 30. URL: www.kommersant.ru /doc/4693875 (дата обращения: Q1.Q8.2Q24).
- Плохинский H.A. Алгоритмы биометрии. М.: МГУ, 198Q. 15Q с.
- Плохинский H.A. Биометрия. Новосибирск: Изд-во СО АН СССР, 1961. 364 с.
- Плохинский H.A. Биометрия / 2-е изд. М.: Изд-во МГУ, 197Q. 363 с.
- Плохинский H.A. Математические методы в биологии: Учеб. -метод. пособие для студентов биол. фак. ун-тов. М.: Изд-во МГУ, 1978. 265 с.
- Плохинский H.A. Печорское скотоводство (данные экспедиции 1928 г.). Архангельск: Волна, 1929. 170 с.
- Плохинский H.A. Статистические методы в зоотехнии. Часть 1. М.: Сельхозгиз, 1937. 181 с.
- Пузаченко Ю.Г. Математические методы в экологических и географических исследованиях: учебное пособие для студентов вузов, обучающихся по географии и экологическим специальностям. М.: Academia, 2004. 407 с.
- Розенберг Г.С. Адольф Кетле и модели логистического роста // Самарская Лука: проблемы региональной и глобальной экологии. 2Q21. Т. 3Q, № 3. С. 78-85.
- Розенберг Г.С. Десять программ обработки экспериментальных данных на ЭВМ "Наири-К". Препринт Ин-та биол. БФАН СССР. Уфа, 1976. 34 с.
- Розенберг Г.С. Дисперсионный анализ в экологии (к 130-летию со дня рождения Рональда Фишера) // Самарская Лука: проблемы региональной и глобальной экологии. 2Q2Q. Т. 29, № 2. С. 132-154.
- Рокицкий П.Ф. Биологическая статистика. Минск: Вышэйш. школа, 1964. 326 с.
- Рындина С.В. Бизнес-аналитика на основе больших данных: обучение без учителя на языках Python и R: учеб.-метод. пособие. Пенза: Изд-во ПГУ, 2Q2Q. 76 с. URL: elib.pnzgu.ru/files/eb/lY4Rmt9mWD84.pdf (дата обращения: 01.08.2024).
- Серебровский А.С. Статистический метод в биологии // Статистический метод в научном исследовании: Опыт коллективной интернаучной работы. М.: Изд-во Ком. акад., 1925. С. 130-165.
- Сиделев С.И. Математические методы в биологии и экологии: введение в элементарную биометрию: учебное пособие. Ярославль: ЯрГУ, 2012. 140 с. URL: www.lib.uniyar.ac.ru/edocs/iuni/20110318.pdf?ysclid=m 3tx0qtwxw392560805 (дата обращения: 01.08.2024).
- Соколов И.Д., Соколова Е.И., Трошин Л.П., Медведь О.М., Колтаков О.М., Наумов С.Ю. Биометрия: учебник / Под общ. ред. Л.П. Трошина. Краснодар: КубГАУ, 2018. 161 с. URL: lnau.su/wp-content/uploads/2021/04/4.-biometriya.pdf (дата обращения: 01.08.2024).
- Терентьев П.В., Ростова Н.С. Практикум по биометрии. Л.: Изд-во ЛГУ, 1977. 152 с.
- Урбах В.Ю. Биометрические методы. Статистическая обработка опытных данных в биологии, сельском хозяйстве и медицине / 2-е изд. М.: Наука, 1964. 415 с.
- Шеффе Г. Дисперсионный анализ / 2-е изд. М.: Наука, 1980. 512 с.
- Шитиков В.К., Мастицкий С.Э. Классификация, регрессия и другие алгоритмы Data Mining с использованием R. 2017. URL: ranalytics.github.io /data-mining/index.html (дата обращения: 01.08.2024).


