Роль и значение математической речи

Математический язык - это совокупность средств, с помощью которых можно выразить математическое содержание. К таким средствам относятся математические термины, графики, схемы, символы, диаграммы и т. д. [1].

Изучение математического языка и ознакомление с его компонентами обязательно при обучении математике. Впервые ученики встречаются с искусственным языком математики еще в начальной школе. В нем так же присутствуют некоторые правила синтаксиса и семантики. Синтаксис указывает на правила использования математических знаков в равенствах, неравенствах, выражениях и других предложениях математического языка. Семантика определяет смысловое значение каждого математического знака [2].

В средней школе вопрос правильного написания и произношения на математическом языке встает острее, т. к. учащиеся сталкиваются с новыми множествами чисел, а сложность изучаемого материала увеличивается. Для каждого ученика важно понимать математический язык, на котором говорит учитель, а также грамотно излагать свои мысли при ответах.

Математическая речь - средство для выражения математических мыслей, их образования и развития. Она подчиняется всем правилам речи, известным из русского языка и литературного чтения. Развитая речь представляется прежде всего содержательной, связной и правильной речью. Умением грамотно излагать полученные знания и выражать свои мысли [3].

Математическая речь не имеет специально оформленную классификацию и подразделяется на следующие направления – устную и письменную речь.

• 1.    Устная математическая речь:

• -    формирование фонетических навыков (представляет собой работу над правильным произношением чисел, переменных и их степеней, а также выразительным чтением определений, теорем, формул и т. д.);

• ‒    формирование словарных навыков (представляет собой работу над пониманием и усвоением прочитанного или услышанного материала, умением составлять грамотные содержательные ответы и вопросы);

• -    качество речи (представляет собой работу над выразительностью, точностью и содержательностью речи, а также над устранением речевых недостатков: избежание тавтологии, косноязычности и «слов – паразитов».

• 2.    Письменная математическая речь:

• ‒    оформление в виде связного текста (определение понятия);

• ‒    оформление в виде рисунка (изображение понятия);

• ‒    оформление в виде схемы (схематическое определение понятия);

• ‒    оформление с применением символики (символическое определение понятия);

• ‒    оформление в виде таблицы (классификация понятий и др.).

Говоря об устной речи, мы подразумеваем последовательность мыслей, озвученную вслух, а письменную, через грамотное оформление, которое демонстрирует ход работы учащегося.

Приведем несколько методических приемов, способствующих развитию содержательной и грамотной математической речи. Самый распространенный и действенный приём - это устное пояснение производимых действий учащимся. Например, при ответах «у доски» или с места математическая речь совершенствуется быстрее всего благодаря тому, что учащийся объясняет свои записи громко и четко на весь класс. Возникновение спорных ситуаций о правильности решения той или иной задачи, исправление неточностей или дополнение ответа стоит решать с помощью постановки дополнительных вопросов, которые будут наводить отвечающего на более точный ответ. Умение слышать и понимать речь одноклассника развивается «при работе в парах или группах», поэтому важно уделить время на ответ каждого учащегося.

Составляя задания для развития математической речи, необходимо учитывать цель, которую нужно достичь: улучшение устной или письменной речи. Так же важно учитывать возраст ученика, составляя задания различной сложности для обучающихся начальной, средней и старшей школы.

Примеры заданий по развитию математической речи учащихся средней школы:

Задание 1. Составьте к словосочетанию «значение произведения» как можно больше определений.

Задание 2. Сконструируйте математические определения, расставив слова в нужном порядке:

• 1)    «Равенство, уравнением, математическое, с одной, или, неизвестными, несколькими, называется».

• 2)    «Это, фигуры, длин, сторон, сумма, периметр, всех».

• 3)    «Четырехугольник, углами, это, с равными, квадрат, сторонами».

• 4)    «Произведение, длины, это, параллелепипеда, и высоты, объем, его, ширины».

• 5)    «Отрезок, серединой, медиана, соединяющий, стороны, это, вершину, с, треугольника, противоположной».

Задание 3. Расставьте ударение в словах: произведение, дециметр, параллелограмм, километр, вычислить, округление, трапеция, уменьшаемое, количество.

Задание 4. Составьте задачу на работу и производительность, используя числа 15, 6, 21: 1) в одно действие; 2) в два действия; 3) в три действия; 4) с вопросом «на сколько»; 5) с вопросом «во сколько раз».

Задание 5. Дайте определения математическим терминам: числитель, целые числа, неравенство, произведение, уменьшаемое, процент, частное, пропорция.

Задание 6.

• а)    Составьте задачу на движение, используя рис. 1.

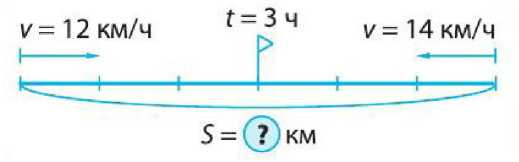
Рис. 1. Чертеж задачи на движение

• б)    Составьте задачу на части, используя рис. 2 (см. на с. 183).

  м

  
  
  

  Б

  Рис. 2. Чертеж задачи на части

  
  

• в)    Составьте задачу на движение по реке, используя данные из табл.

Таблица

Данные для задачи на движение

	Скорость	Время	Расстояние
По течению	(10+2) км/ч	? ч	24 км
Против течения	(10–2) км/ч	? ч	24 км
Лодка	10 км/ч	–	–
Река	2 км/ч	–	–

Задание 7. Вставьте пропущенные буквы в математических терминах: «выч_тание», «сл_же-ние», «пр_цент», «дес_тичная дробь», «ур_внение», «знам_натель», «ч_слитель», «умн_жение», «д_ литель», «дискр_м_нант», «_ксиома», «к_нстанта».

Задание 8. Вставьте пропущенные слова так, чтобы получились верные математические определения:

• 1.    Обыкновенная дробь называется …, если ее числитель … знаменателя.

• 2.    Произведение … членов пропорции равно произведению … членов этой же пропорции.

• 3.    Чтобы сложить две дроби с … знаменателями, нужно сложить их числители, а … оставить без изменения.

• 4.    Чтобы разделить две дроби, нужно перевернуть делитель, и заменить деление …. Задание 9. Найдите неточности в пояснениях.

  

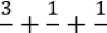
• а)    Объясняя ход вычислений в примере          , Дима ответил следующее: «Чтобы сложить

дроби с различными знаменателями, нужно привести дроби к общему знаменателю, а затем прибавить числители со знаменателями». Является ли ответ Димы правильным? Какие речевые ошибки допущены?

• б)    Решив пример 15,02+2,5=17,52, Света ответила: «У меня получилось 17,52. Я уравняла количество знаков после запятой у слагаемых и выполнила сложение». Является ли ответ Светы полным? Что упустила девочка при пояснении своего решения.

• в)    «Для нахождения степени одночлена 4a²b³ нужно просуммировать показатели степеней всех множителей, входящих в одночлен. Степень числа 4 - 1, a - 2, b - 3. Степень данного одночлена - 6», - ответила Таня. Верно ли посчитала девочка?

Задание 10. Соедините написание и произношение дробей.

• 1)    1,001 а) Девять целых три седьмых.

• 2)          б) Четыре целых семь сотых.

  

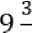
• 5)    1,504     д) Ноль целых семь десятых.

• 6)    4,07      е) Ноль целых семь сотых.

• 7)    0,07 ж) Одна пятая.

Задание 11. Решите уравнения:

• 1)    4х=2(х-1)

• 2)    -3(2х-5)=5-х

• 3)    2-(8х+4)=-6х

• 4)    (х+3)²=-(3-х² + 6х)

• 5)    (х-2)(х+2)=х²-2(3х-7)

Ответы:

Задание 1. «Значение произведения» – это …

‒ результат действия умножения;

‒ число, равное нулю, если хотя бы один из множителей равен нулю;

• - число, при делении которого на один из множителей получается другой множитель или произведение оставшихся множителей;

‒ число, которое остается неизменным, при перестановке множителей местами.

Задание 2.

• 1)    Уравнением называется математическое равенство с одной или несколькими неизвестными переменными.

• 2)    Периметр – это сумма длин всех сторон фигуры.

• 3)    Квадрат – это четырехугольник с равными сторонами и углами.

• 4)    Объем параллелепипеда – это произведение его длины, ширины и высоты.

• 5)    Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Задание 3. Расставьте ударение в словах: произведЕние, децимеЕтр, параллелогрАмм, киломЕтр, вЫчислить, округлЕние, трапЕция, уменьшАемое, колИчество.

Задание 4.

• 1.    Первый мастер изготавливает 15 деталей за день, его помощник 6 деталей за день. Сколько деталей мастер и его ученик изготавливают за день вместе?

• 2.    Первый мастер изготовил 15 деталей за день, его ученик 6 деталей. Второй мастер изготовил на 3 детали больше, чем первый мастер. Сколько деталей изготавливает ученик второго мастера, если вместе они изготавливают 21 деталь?

• 3.    Ученик изготавливает 5 деталей в день. Вместе с мастером за 4 дня они изготовили 80 деталей. Сколько деталей изготовил бы мастер за 3 дня, работая один.

• 4.    Мастер изготавливает 27 деталей за 3 дня, а его ученик 9 деталей. На сколько производительность мастера больше, чем ученика?

• 5.    Во сколько раз производительность мастера больше, чем его ученика, если мастер за 3 дня изготовил 27, а его ученик 9 деталей?

Задание 5.

Числитель – верхнее число в дроби.

Целые числа – это множество, состоящее из натуральных чисел, им противоположных и нуля.

Неравенство – это алгебраическое выражение, составленное с помощью знаков сравнения: ≠, <,>, ≤, ≥.

Произведение – число, полученное в результате умножения.

Уменьшаемое – число, из которого вычитают.

Процент – одна сотая часть числа.

Пропорция – равенство двух отношений.

Задание 6.

• а)    Два друга выплыли на встречу друг к другу на байдарках в стоячей воде и встретились через 3 часа. Первый плыл со скоростью 12 км/ч, а второй на 2 км/ч быстрее. Какое расстояние было между друзьями в начале пути?

• б)    У бабушки на кухне находится 4 миски и 12 блюдец. На сколько мисок меньше, чем блюдец?

• в)    Лодка с отдыхающими преодолела путь от пристани до соседнего острова в 24 км. Скорость лодки 10 км/ч, скорость течения реки 2 часа. Сколько времени длилось путешествие отдыхающий?

Задание 7. Вставьте пропущенные буквы в математических терминах: «вычИтание», «слОжение», «прОцент», «десЯтичная дробь», «урАвнение», «знамЕнатель», «чИслитель», «умнОжение», «дЕлитель», «дискрИмИнант», «Аксиома», «кОнстанта».

Задание 8.

• 1.    Правильной, меньше/неправильной, больше.

• 2.    Крайних, средних.

• 3.    Одинаковыми, знаменатель.

• 4.    Умножением.

Задание 9.

• а)    Ответ Димы не точный. После приведения дробей к общему знаменателю складываются только числители.

• б)    Ответ Светы не полный. После уравнивания количества знаков после запятой необходимо выполнить сложение, не обращая внимания на запятую. Далее уже в конечном ответе поставить запятую под запятой.

• в)    Неправильно, степень одночлена находится путем сложения степеней только переменных. Степень одночлена – 5.

Задание 10.

1 – г, 2 – ж, 3 – а, 4 – д, 5 – в, 6 – б, 7 – е.

Задание 11. Решите уравнения:

• 1)    4х = 2(х-1)

4х = 2х - 2

4х - 2х = -2

2х = -2

х = -1

• 2)    -3(2х-5) = 5 - х

  -6х + 15 = 5 – х

  -6х + х = 5 – 15

  -5х = -10

х = 2

• 3)    2 – (8х+4) = -6х

2 – 8х – 4 = -6х

-8х+6х = 2

-2х = 2

х = -1

• 4)    (х+3)² = - (3-х² + 6х)

х2 + 6х + 9 = -3+ х2 – 6х х2 + 6х - х2 + 6х = -3 – 9

12х = -12

х = -1

• 5)    (х-2)(х+2) = х²-2(3х-7)

х2 - 4 = х2- 6х + 14

х2– х2 +6х = 14 + 4

6х = 18

х = 3